QiYun

Note

3D Model

Posted on Edited on In
2.7k 10 mins.

三维模型的各种形式，初步探索

  • 构造实体几何(eg: CAD)
  • 多边形网格(eg: FEA)
    • 近似网格编码——曲面细分
    • 精确网格编码——样条(NURBS)
  • 箱体建模(eg: 雕刻模型 for 游戏/电影)

3D Represent

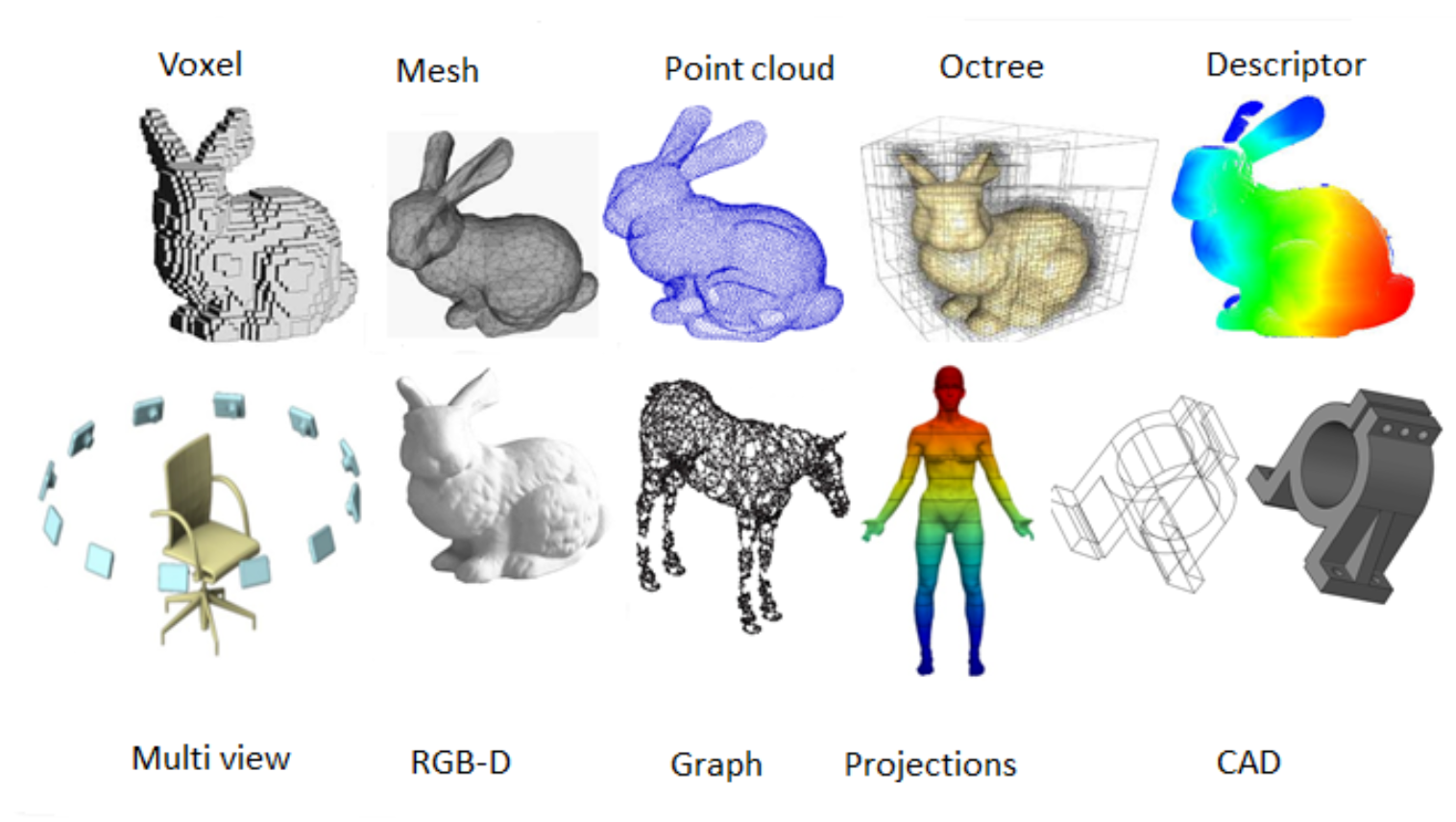
image.png|666

10种最流行的3D文件格式 - BimAnt
什么是计算机图形学

目前，机械行业中不同的模型形式：

  • 构造实体几何Constructive solid geometry - Wikipedia，构造实体几何允许建模者通过使用布尔运算符组合更简单的对象来创建复杂的表面或对象，从而可能通过组合一些原始对象来生成视觉上复杂的对象。(Solidworks、AutoCAD等机械设计的三维模型)
  • 多边形网格Polygon mesh - Wikipedia，面通常由三角形（triangle mesh）、四边形（quads）或其他简单凸多边形（n-gons）组成。多边形网格也可能更通常由凹多边形或带有孔的偶数多边形组成。体积网格与多边形网格的不同之处在于，它们显式表示结构的表面和内部区域，而多边形网格仅显式表示表面（体积是隐式的）。(3D打印、CAE仿真)
    • 近似网格编码，3D 模型的表面覆盖有微小多边形（通常是三角形）的网格。 此过程也称为“曲面细分”，因此这些文件格式也称为曲面细分格式。
    • 精确网格编码，精确文件格式使用非均匀有理基样条 (NURBS，一种计算机生成的数学模型）形成的曲面，而不是多边形。对于一些复杂的连接处需要用到样条来表示
  • 箱体建模Box modeling - Wikipedia，长方体建模是 3D 建模中的一种技术，其中使用基本形状（例如长方体、圆柱体、球体等）来制作最终模型的基本形状。然后使用这个基本形状来雕刻最终模型。该过程使用许多重复的步骤来达到最终产品，这可以导致更高效、更可控的建模过程。(艺术家雕刻过程)

Solid

目前机械行业使用最多的模型形式

获取

人工建模Solidworks、Creo、Rhino…

强化学习重建CAD模型：3D reconstruction based on hierarchical reinforcement learning with transferabilit

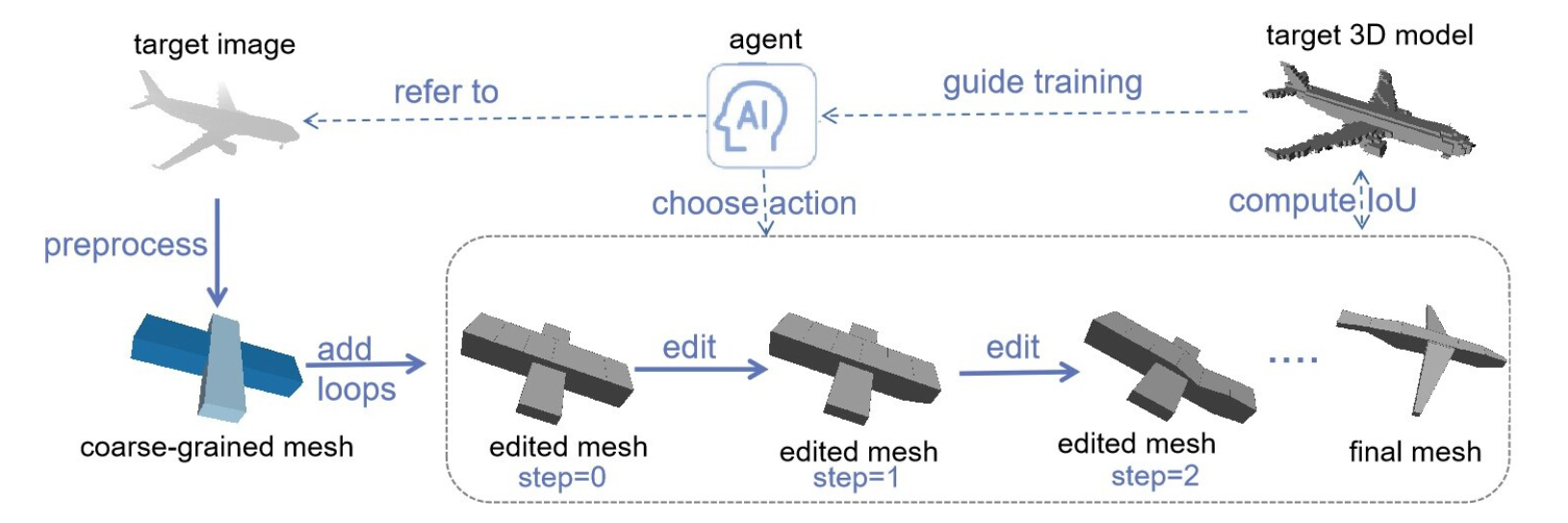
image.png|666

从FE surface mesh model中提取 free-form B-spline surface：Surface reconstruction from FE mesh model

m_j.jcde.2018.05.004-fx1.jpeg (520×297)|666

Polygon mesh

其中网格(mesh)为各个领域最常用的表示方法，其可以分为surface mesh和volume mesh：

  • 表面mesh：通过多个三角形/四边形组成物体表面，可用于3D打印
  • 体mesh：通过多个四面体网格tet/六面体网格hex/其他网格组成实体模型，可用于CAE

surface mesh

获取

  • 人工建模：通过直接操纵顶点、边和面来创建和编辑模型。常见的手动建模工具有Autodesk 3ds Max、Blender、Maya等，支持多边形建模、细分曲面建模、NURBS建模(非均匀有理B样条曲线和曲面)等多种技术
  • 扫描建模：通过3D扫描设备（如激光扫描仪、结构光扫描仪、深度相机）获取实物的点云数据，再通过软件（如Meshlab、CloudCompare、Geomagic）进行点云处理、网格化，生成精确的三维模型
  • 根据图片使用算法进行建模(成本低) Paper About 3D Reconstruction
    • 显示表示，获取点云/体素/深度图等后然后转mesh，或者直接获取mesh
      • COLMAP通过SFM获取相机位姿+稀疏点云，并使用MVS来估计深度图并通过depth fusion来获取稠密点云，最后通过screened poisson surface reconstruction获取mesh
      • 3DGS(SuGaR) 高斯体的中心点即为物体点云，然后可以转mesh
    • 隐式表示：IDR/DVR、NeRF(VolSDF、NeuS)使用MC算法从隐式场中提取物体表面mesh
    • ….

其他：

NumGrad-Pull: Numerical Gradient Guided Tri-plane Representation for Surface Reconstruction from Point Clouds. CuiRuikai/NumGrad-Pull

GdX2bOjaoAM3EUG (1697×980)|666

优化

从低质量的dense mesh/点云中生成高质量人造Mesh(网格规律，缺陷少)：

teaser.png (6507×6449)|666

Other

计算3D surface mesh的体积
math - How to calculate the volume of a 3D mesh object the surface of which is made up triangles - Stack Overflow | chenlab.ece.cornell.edu/Publication/Cha/icip01_Cha.pdf

volume mesh

获取

有限元网格划分：Finite Element Model 3D Reconstruction | Anime Image 3D Reconstruction

surface mesh转volume mesh

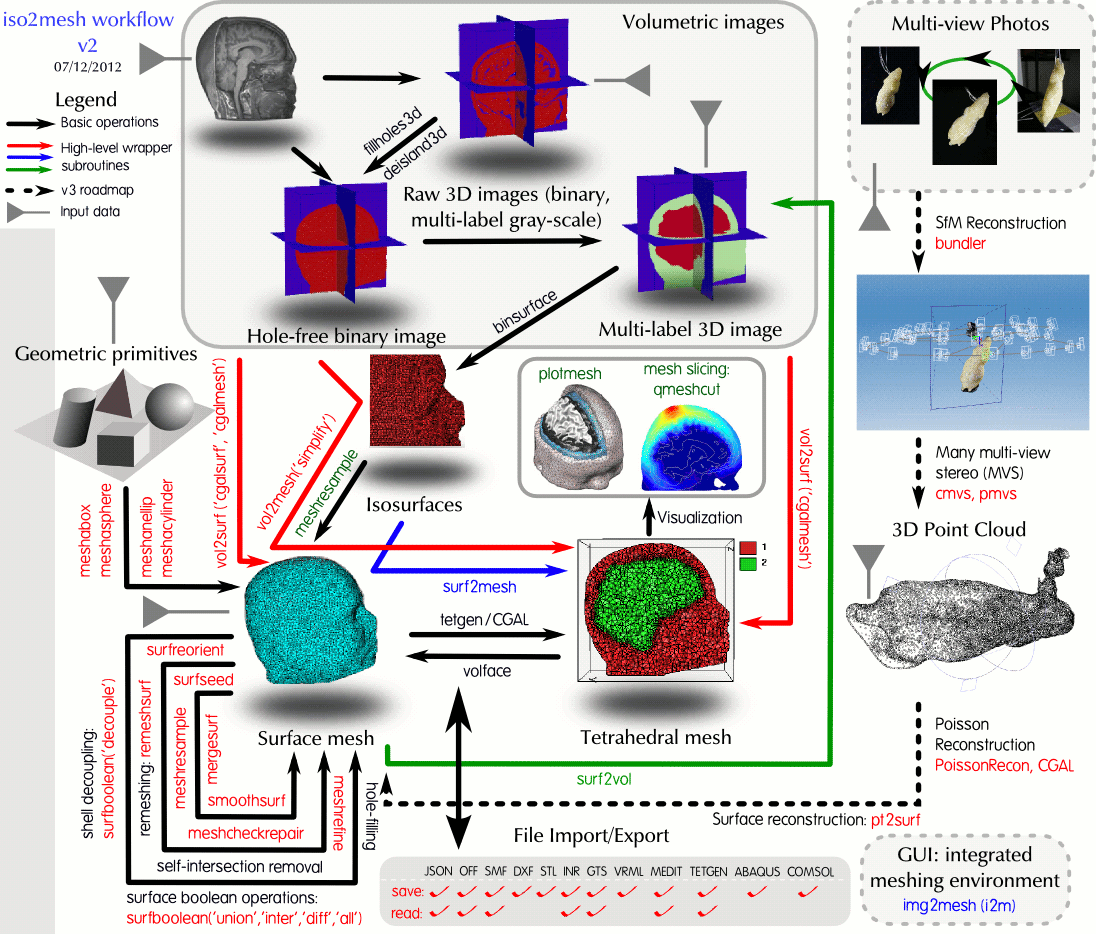
iso2mesh_workflow_v2.png (1096×934)|666

VMesh: Hybrid Volume-Mesh Representation for Efficient View Synthesis
这篇文章是使用混合volume mesh表示来高效地生成新试图，那么用体渲染思路来优化volume mesh可行否？

生成式方法：

优化

Fast and Robust Hexahedral Mesh Optimization via Augmented Lagrangian, L-BFGS, and Line Search | PDF
X 上的 Zhenjun Zhao：“Fast and Robust Hexahedral Mesh Optimization via Augmented Lagrangian, L-BFGS, and Line Search Hua Tong, Yongjie Jessica Zhang https://t.co/XAjGcAZxMp https://t.co/yu7zDYbdHY” / X

精确网格/样条

贝塞尔曲线 深入理解贝塞尔曲线贝塞尔曲线于 1962 年，由法国工程师皮埃尔·贝济埃（Pierre Bézier）所广泛发表，他运用 - 掘金

n阶贝塞尔曲线： $B(t)=\sum_{i=0}^nC_n^iP_i(1-t)^{n-i}t^i,t\in[0,1]$ 或者 $B(t)=\sum_{i=0}^nP_ib_{i,n}(t)\text{,}t\in[0,1]$

  • $P_{i}$为控制点，通过n+1个控制点控制
  • $b_{i,n}(t)$为基函数
  • 阶数为n，表示拟合曲线多项式的最高次方

B样条曲线和Nurbs曲线 图文并茂的理解节点和节点区间 - 知乎

B样条曲线与Bezier曲线不同的是，其将控制点进行了分组，每几个控制点合并为一个“群组”，在“群组”内采用自定义阶数 k 的基函数的组合来拟合曲线： $P(t)=\sum_{i=0}^{n}N_{i,k} (t)P_{i}$ ，其中$N_{i,k}(t)$阶数k，次数为k-1(定义有混淆)，k阶曲线需要k+1个控制点。
(塞尔曲线的控制点“牵一发而动全身”、B样条曲线的控制点只影响“局部范围”)

Bezier曲线可以视为均匀有理B样条，非均匀有理B样条(Non-uniform rational B-spline)：
非均匀有理B样条 - 维基百科，自由的百科全书

Traditional FEA vs Spline-based and Isogeometric FEA - YouTube

等几何分析（1） - NoN的文章 - 知乎 等几何分析，将原来FEA在单元节点上的插值计算，变为在控制网格点上的插值计算，IGA目前主要问题在剪裁样条曲面和大量样条碎片难以处理上，且由于基函数比较复杂，有时候对于非线性问题求解容易发散，数值求解并不问题。个人认为IGA面临的问题不在于力学上，而是在几何和拓扑上，如果更好的解决复杂几何体的连续性、重构等问题，那么对IGA的推广应该有很大裨益。

Discontinuous Galerkin Methods for Isogeometric Analysis

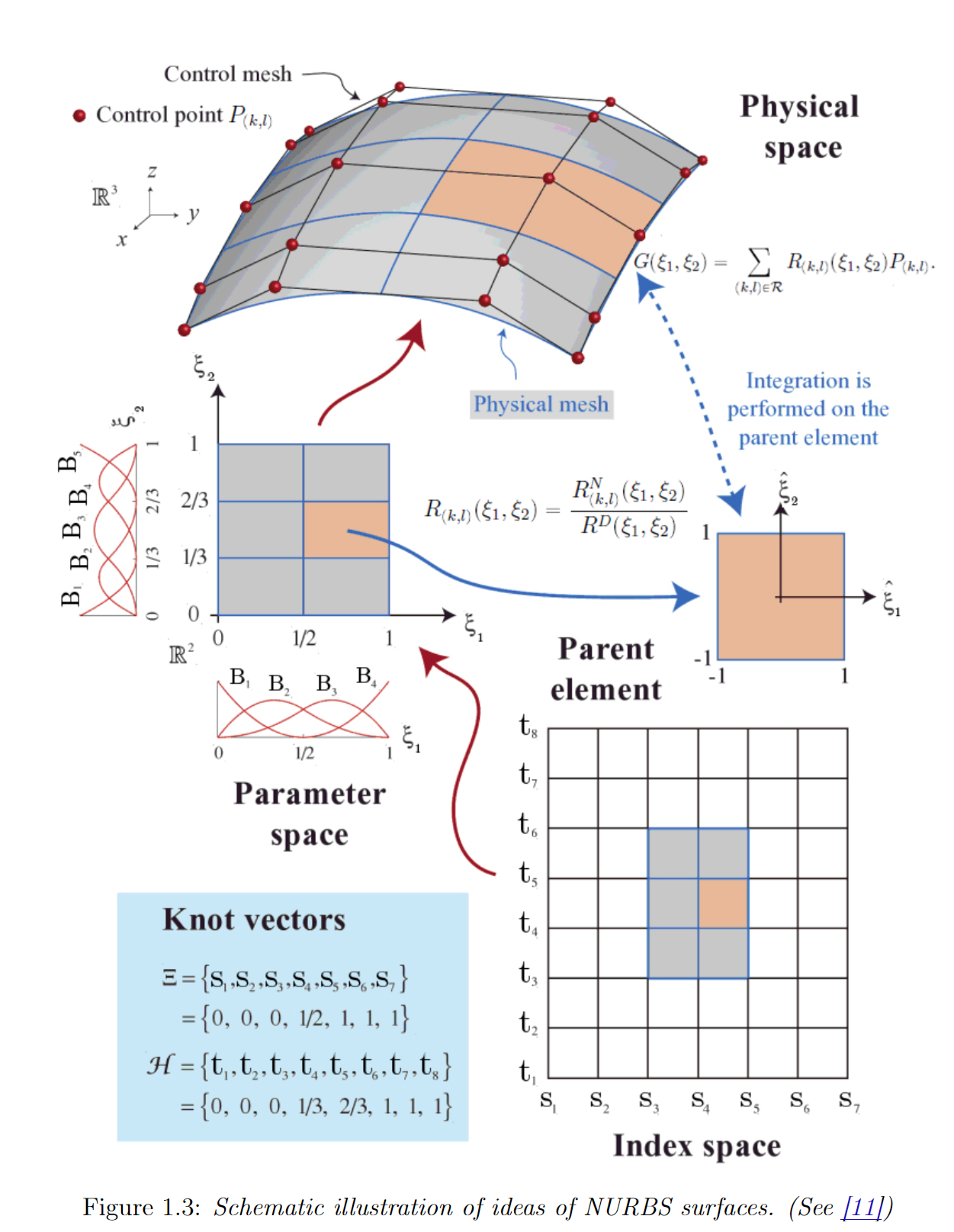
image.png|444

面向等几何分析的区域参数化方法研究 博论 jiyess.github.io/files/pdf/publications/thesis_compressed.pdf

IGA: A Simplified Introduction and Implementation Details for Finite Element Users

Isogeometric analysis (IGA) is a recently introduced technique that employs the Computer Aided Design (CAD) concept of Non-uniform Rational B-splines (NURBS) tool to bridge the substantial bottleneck between the CAD and finite element analysis (FEA) fields

GAMES Webinar 306-CAD/CAE/CAM专题-魏小东-面向复杂几何的优化设计与分析_哔哩哔哩_bilibili

实现复杂几何的一体化表征(CAD/CAE)：

  • 非结构化样条： CAD变、CAE不变
  • 非协调元：CAD不变、CAE变

【Freya｜熟肉】线条函数的连续性_哔哩哔哩_bilibili

贝塞尔 spline：分段三阶贝塞尔曲线构成的曲线，各段之间有三种连接形式：

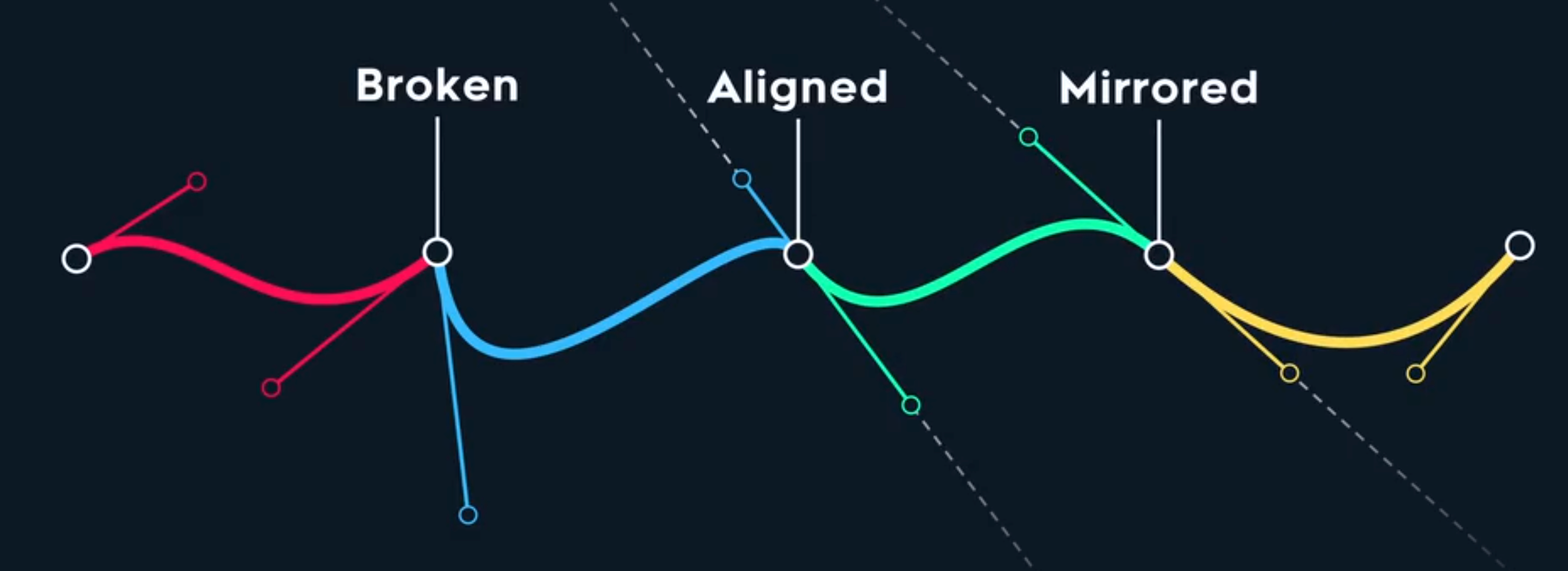
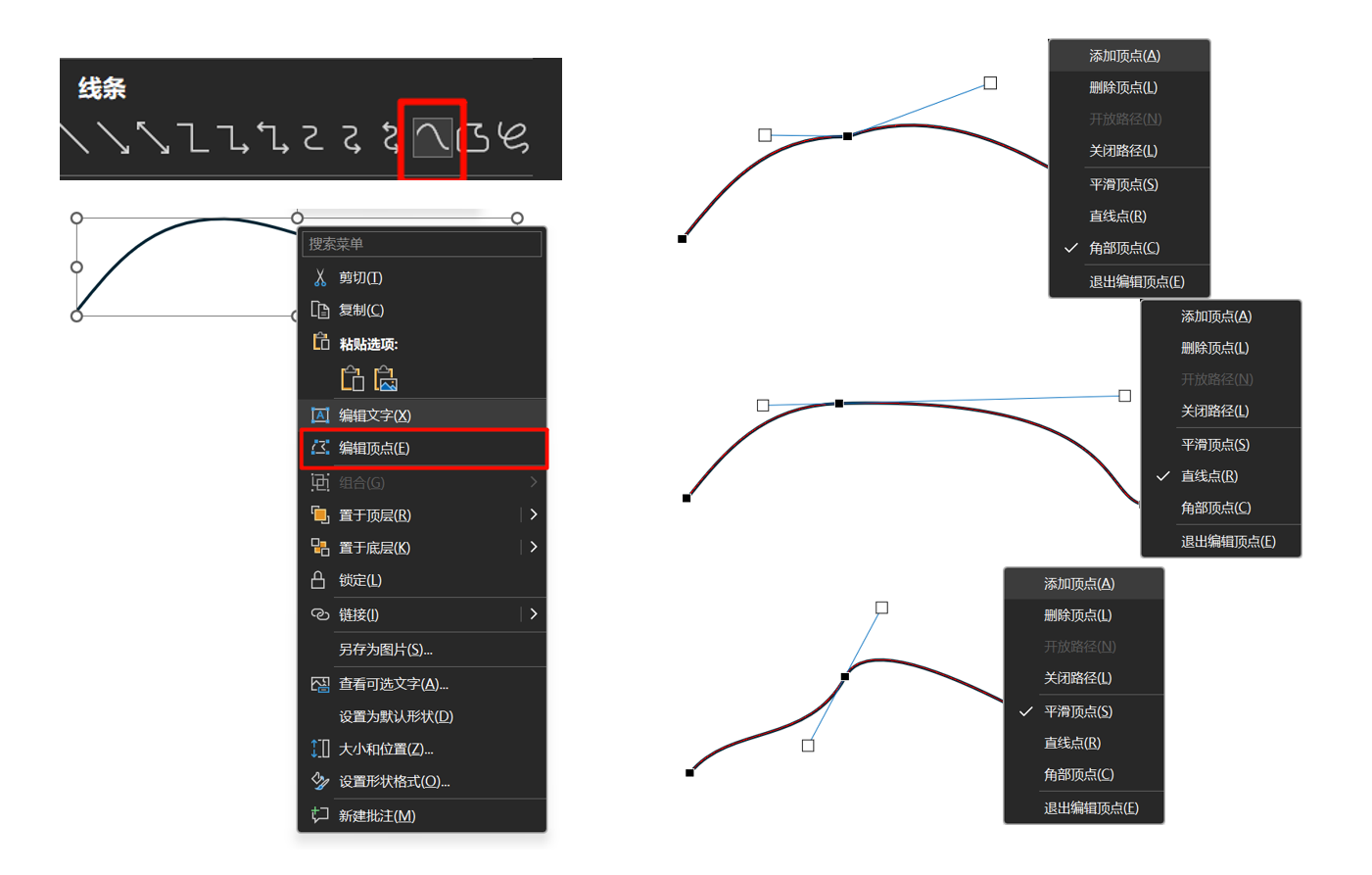
image.png|444

PPT中的曲线构建用的就是这种方法

image.png|444

Broken 和 Aligned曲线是$C^{0}$连续的，但是其速度/一阶导数不连续
Mirrored 曲线则可以做到$C^{1}$连续，且同时必须是$C^{0}$连续的，
然而他们都不是$C^{2}$连续的，如果要构建$C^{2}$甚至$C^{3}$连续的曲线，则对于三阶贝塞尔曲线来说，可以控制的点会很少，只移动一个点，其他点都会发生很大的变动，无法构成一条曲线。

定义：两个函数A和B，如果在连接点出的0~n阶导数都相等，则他们是$C^{n}$连续的(参数连续性)

Aligned曲线虽然在连接点处的速度有变化，但是其速度方向单位向量/法向向量始终保持不变，这被称为切线连续性$G^{1}$(几何连续性)

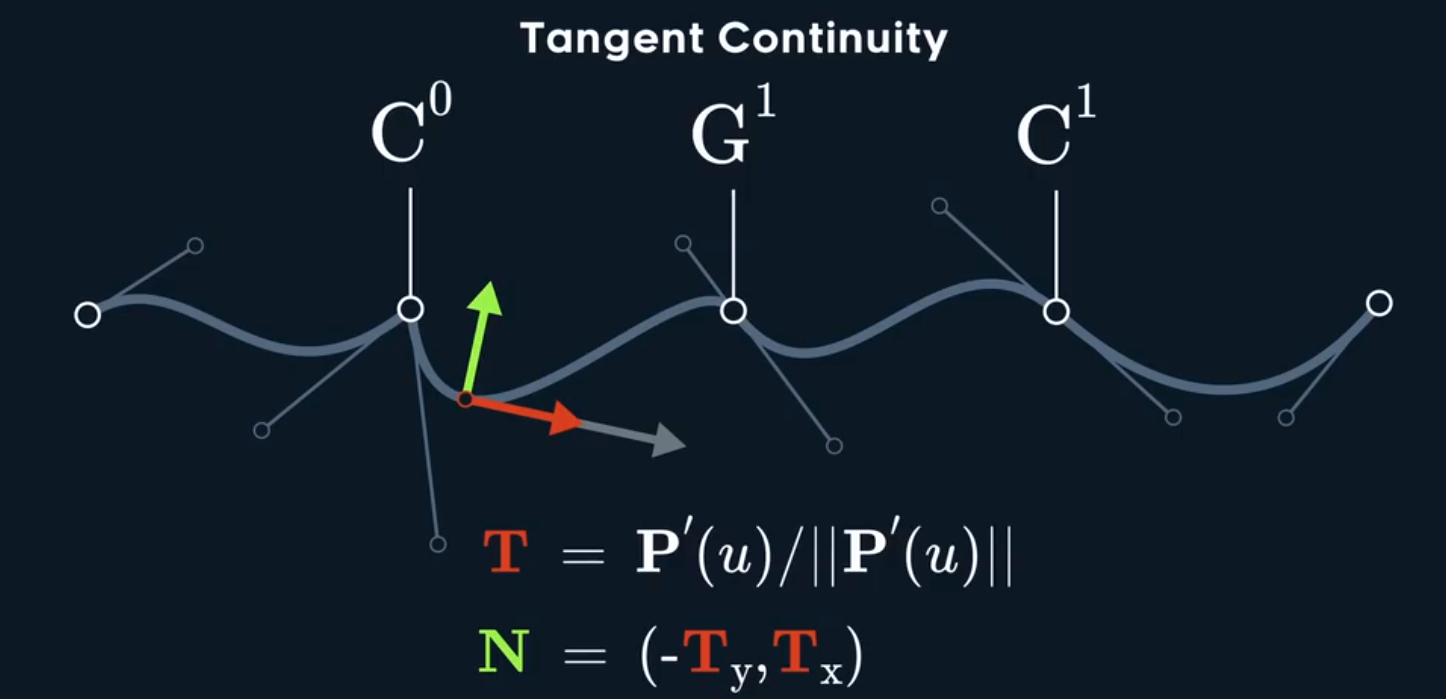
image.png|444

$G^{2}$连续性—>考虑曲率，曲率连续性(曲率梳是连续的)，$G^{3}$连续性—>曲率梳的导数(变化率)是连续的
曲率$\kappa=\frac{\begin{vmatrix}\mathbf{P}^{\prime}&\mathbf{P}_x^{\prime\prime}\\\mathbf{P}^{\prime}&\mathbf{P}_y^{\prime\prime}\end{vmatrix}}{||\mathbf{P}^{\prime}||^3}$，半径为$1/\kappa$的圆

定义：两个曲线A和B，如果存在函数g(t)使得A(t)和B（g(t)）是$C^{n}$连续的，则两者是$G^{n}$连续的

了解了连续性的定义后，可以拓展其他的样条曲线：

固定曲线起点和终点位置，设置边界条件，求解曲线中间的控制点位置

  • Hermite Spline，曲线两端点速度相同(已知边界速度)
  • Linear Spline，直接连接两点成直线
  • Cardinal Spline，每个点的速度为相邻两点的方向向量乘以一个缩放因子
    • Catmull-Rom Spline，缩放因子为1/2
  • Basis Spline $C^{2}$连续的
  • Non-Uniform Rational B-Spline NURBS
    • Non-Uniform：改变节点值，每条曲线使用基于节点值的独特基函数
    • Rational：可以控制每个控制点的优先级/权重值，使得曲线向特定控制点靠拢或者远离

Linear Spline 控制点特别多的时候，可以用线性来模拟非线性，FEA

样条的应用：也可以看成一个可控轨迹函数

  • CAD/CAE
  • 相机轨迹生成
  • 动画的轨迹，物体位置/角度/大小，随时间的变化曲线
  • 颜色空间采样曲线，将灰度图片映射为特定颜色空间的图片
  • …

Welcome to my other publishing channels