| Title | Plenoxels: Radiance Fields without Neural Networks |
|---|---|
| Author | Sara Fridovich-Keil and Alex Yu and Matthew Tancik and Qinhong Chen and Benjamin Recht and Angjoo Kanazawa |
| Conf/Jour | CVPR |
| Year | 2022 |
| Project | sxyu/svox2: Plenoxels: Radiance Fields without Neural Networks (github.com) |
| Paper | Plenoxels: Radiance Fields without Neural Networks (readpaper.com) |
Abstract
我们介绍了 Plenoxels(plenoptic voxels),一个用于真实感视图合成的系统。Plenoxels 将场景表示为带有球面谐波的稀疏3D 网格。这种表示可以通过梯度方法和正则化从校准的图像中优化,而不需要任何神经成分。在标准的基准任务中,Plenoxels 的优化速度比 Neural Radiance Fields 快两个数量级,而视觉质量没有损失。有关视频和代码,请参阅 https://alexyu.net/plenoxels 。
我们的实验表明,神经辐射场的关键元素不是神经网络,而是可微体积渲染器
Classical Volume Reconstruction
使用一个更比八叉树简单的稀疏数组结构。将这些基于网格的表示与某种形式的插值相结合,产生一个连续的表示,可以使用标准信号处理方法任意调整大小
Neural Volume Reconstruction
Neural Volumes[20]与我们的方法最相似,因为它使用带有插值的体素网格,但通过卷积神经网络优化该网格,并应用学习的扭曲函数来提高(1283 网格)的有效分辨率。我们证明了体素网格可以直接优化,并且可以通过修剪和粗到细的优化来实现高分辨率,而不需要任何神经网络或扭曲函数。
Accelerating NeRF.
我们的方法扩展了 PlenOctrees,对具有球面谐波的稀疏体素表示进行端到端优化,提供了更快的训练(与 NeRF 相比加速了两个数量级)。我们的 Plenoxel 模型是 PlenOctrees 的泛化,以支持任意分辨率(不需要 2 的幂)的稀疏全光学体素网格,并具有执行三线性插值的能力,使用这种稀疏体素结构更容易实现
Method
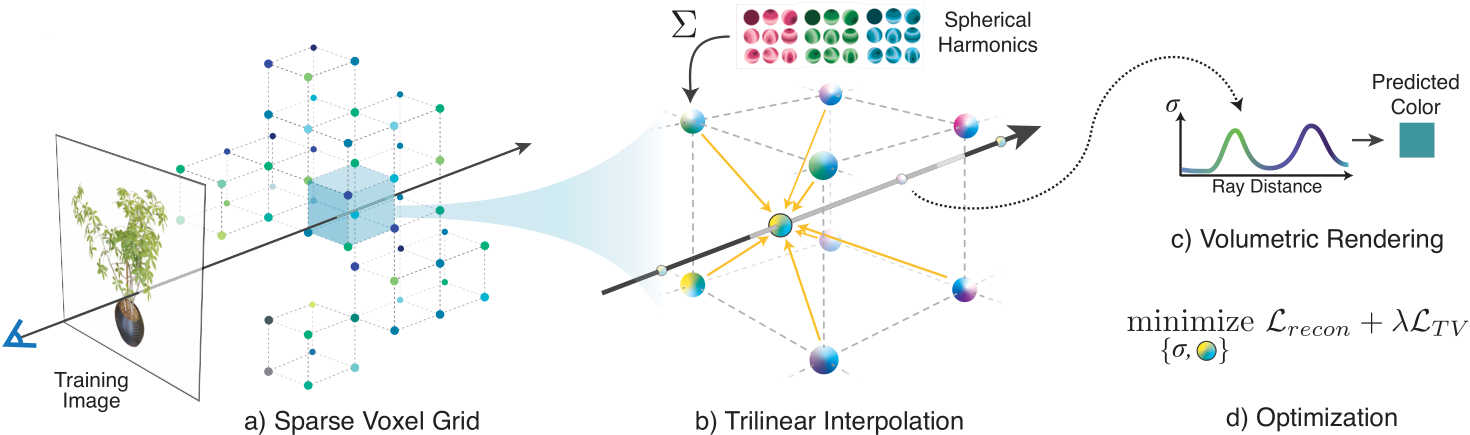
我们的模型是一个稀疏体素网格,其中每个被占用的体素角存储一个标量不透明度σ和每个颜色通道的球谐系数向量。从这里开始,我们把这种表现称为 Plenoxel。在任意位置和观察方向上的不透明度和颜色是通过对相邻体素存储的值进行三线性插值,并在适当的观察方向上计算球面谐波来确定的。给定一组校准图像,我们直接使用训练光线的渲染损失来优化我们的模型。我们的模型如图 2 所示,并在下面进行详细描述。
- Volume Rendering 与 NeRF 相同
- Voxel Grid with Spherical Harmonics 与 PlenOctrees 类似
- 我们不使用八叉树作为我们的数据结构。相反,我们将一个密集的 3D 索引数组与指针存储到一个单独的数据数组中,该数据数组仅包含已占用体素的值
- 与 pleenoctrees 类似,每个占用的体素为每个颜色通道存储一个标量不透明度σ和一个球谐系数向量。球面谐波形成了在球面上定义的函数的正交基,低次谐波编码平滑(更朗伯)的颜色变化,高次谐波编码更高频率(更镜面)的效果
- 样本 ci 的颜色简单地是每个颜色通道的这些谐波基函数的和,由相应的优化系数加权,并在适当的观看方向上进行评估。我们使用 2 degree 的球面谐波,每个颜色通道需要 9 个系数,每个体素总共需要 27 个谐波系数。我们使用 2 次谐波,因为 PlenOctrees 发现高次谐波只带来最小的好处。
- 我们的 Plenoxel 网格使用三线性插值来定义整个体积的连续全光函数。这与 PlenOctrees 相反,PlenOctrees 假设不透明度和球谐系数在每个体素内保持恒定。这种差异是成功优化容量的一个重要因素,我们将在下面讨论。所有系数(不透明度和球面谐波)都是直接优化的,没有任何特殊的初始化或神经网络的预训练
- Interpolation
- 通过存储在最近的 8 个体素处的不透明度和谐波系数的三线性插值计算每条射线上每个样本点的不透明度和颜色。我们发现三线性插值明显优于最近邻插值
- Plenoxel 在固定分辨率下缩小了最近邻和三线性插值之间的大部分差距,但由于优化不连续模型的困难,仍然存在一些差距。事实上,我们发现与最近邻插值相比,三线性插值在学习率变化方面更稳定
- Coarse to Fine
- 我们通过一种从粗到细的策略来实现高分辨率,该策略从低分辨率的密集网格开始,优化修剪不必要的体素,通过在每个维度上将每个体素细分为两半来细化剩余的体素,并继续优化
- 由于三线性插值,天真的修剪会对表面附近的颜色和密度产生不利影响,因为这些点的值会与直接外部的体素进行插值。为了解决这个问题,我们执行一个扩张操作,这样一个体素只有在它自己和它的邻居都被认为是未被占用时才会被修剪。
- Optimization:$\mathcal{L}=\mathcal{L}_{recon}+\lambda_{TV}\mathcal{L}_{TV}$ 根据渲染像素颜色的均方误差(MSE)优化了体素不透明度和球谐系数
- $\mathcal{L}_{recon}=\frac1{|\mathcal{R}|}\sum_{\mathbf{r}\in\mathcal{R}}|C(\mathbf{r})-\hat{C}(\mathbf{r})|_2^2$
- total variation (TV) $\mathcal{L}_{TV}=\frac1{|\mathcal{V}|}\sum_{\underset{d\in[D]}{\operatorname*{v\in\mathcal{V}}}}\sqrt{\Delta_x^2(\mathbf{v},d)+\Delta_y^2(\mathbf{v},d)+\Delta_z^2(\mathbf{v},d)}$
- 为了更快的迭代,我们在每个优化步骤中使用 raysR 的随机样本来评估 MSE 项,并使用体素 V 的随机样本来评估 TV 项
- Unbounded Scenes
- 对于前向场景,我们使用与原始 NeRF 论文[26]中定义的归一化设备坐标相同的稀疏体素网格结构。
- 对于 360 场景,我们用多球体图像(MSI)背景模型增强我们的稀疏体素网格前景表示,该模型还使用球体内部和球体之间的三线性插值来学习体素颜色和不透明度。注意,这实际上与我们的前景模型相同,除了使用简单的等矩形投影将体素扭曲成球体(体素指数超过球体角度θ和φ)。我们将 64 个球体线性地放置在从 1 到∞的逆半径上(我们预缩放内部场景以近似包含在单位球体中)。为了节省内存,我们只为颜色存储 rgb 通道(只有零阶 SH),并通过使用不透明度阈值来稀疏存储所有图层,就像我们的主模型一样。这类似于 nerf++[57]中的背景模型。
- Regularization 对于某些类型的场景,我们还使用额外的正则化器
- 在真实的、正向的和360°的场景中,我们使用基于柯西损失的稀疏先验 $\mathcal{L}_s=\lambda_s\sum_{i,k}\log\left(1+2\sigma(\mathrm{r}_i(t_k))^2\right)$,类似于 PlenOctrees[56]中使用的稀疏度损失,并鼓励体素为空,这有助于节省内存并减少上采样时的质量损失
- 在真实的 360 度场景中,我们还对每个 minibatch 中每条光线的累积前景透射率使用 beta 分布正则化器。这个损失项,在神经体积[20]之后,通过鼓励前景完全不透明或空来促进清晰的前景-背景分解。这个损失是: $\mathcal{L}_{\beta}=\lambda_{\beta}\sum_{\mathbf{r}}\left(\log(T_{FG}(\mathbf{r}))+\log(1-T_{FG}(\mathbf{r}))\right)$
- Implementation
- 由于稀疏体素体渲染在现代自动 diff 库中不受很好的支持,我们创建了一个自定义 PyTorch CUDA[29]扩展库来实现快速可微体渲染;我们希望从业者会发现这个实现在他们的应用程序中很有用。我们还提供了一个更慢、更高级的 JAX[4]实现。这两个实现都将向公众发布
- 我们实现的速度在很大程度上是可能的,因为我们的 Plenoxel 模型的梯度变得非常稀疏,非常快,如图 4 所示。在优化的前 1-2 分钟内,只有不到 10%的体素具有非零梯度。
Discussion
我们提出了一种用于逼真场景建模和新颖视点渲染的方法,该方法产生的结果具有与最新技术相当的保真度,同时减少了训练时间的数量级。我们的方法也非常简单,阐明了解决 3D 逆问题所需的核心要素:可微分正演模型,连续表示(在我们的情况下,通过三线性插值)和适当的正则化。我们承认,这种方法的成分已经存在了很长时间,但是具有数千万变量的非线性优化直到最近才被计算机视觉从业者所接受。
Limitations and Future Work
与任何未确定的逆问题一样,我们的方法容易受到人为因素的影响。我们的方法显示了与神经方法不同的伪影,如图 9 所示,但两种方法在标准度量方面都达到了相似的质量(如第 4 节所示)。未来的工作可能能够通过研究不同的正则化先验和/或更精确的物理可微分渲染函数来调整或减轻这些剩余的伪影。
尽管我们用一组固定的超参数报告了每个数据集的所有结果,但没有权重 $λ_{TV}$ 的最佳先验设置。在实践中,通过在逐场景的基础上调整该参数可以获得更好的结果,这是可能的,因为我们的训练时间很快。这是意料之中的,因为不同场景的训练视图的规模、平滑度和数量是不同的。我们注意到 NeRF 也有超参数需要设置,如位置编码的长度、学习率和层数,并且调整这些也可以在逐场景的基础上提高性能。
我们的方法应该自然地扩展到支持多尺度渲染,并通过体素 cone tracing 提供适当的抗锯齿,类似于 Mip-NeRF[2]中的修改。另一个简单的补充是色调映射,以说明白平衡和曝光的变化,我们希望这将有助于特别是在真实的 360 度场景。与我们的稀疏数组实现相比,分层数据结构(如八叉树)可以提供额外的加速,前提是保留了可微分插值。
由于我们的方法比 NeRF 快两个数量级,我们相信它可能会使下游应用程序目前受到 NeRF 性能的瓶颈,例如,跨大型场景数据库的多重反弹照明和 3D 生成模型。通过将我们的方法与其他组件(如相机优化和大规模体素哈希)相结合,它可能为端到端逼真的 3D 重建提供实用的管道。