Voxurf

Title	Voxurf: Voxel-based Efficient and Accurate Neural Surface Reconstruction
Author	Tong Wu and Jiaqi Wang and Xingang Pan and Xudong Xu and Christian Theobalt and Ziwei Liu and Dahua Lin
Conf/Jour	ICLR
Year	2023
Project	wutong16/Voxurf: [ ICLR 2023 Spotlight ] Pytorch implementation for “Voxurf: Voxel-based Efficient and Accurate Neural Surface Reconstruction” (github.Com)
Paper	Voxurf: Voxel-based Efficient and Accurate Neural Surface Reconstruction (readpaper.com)

依赖 mask 即 rembg 技术

Abstract

神经表面重建的目的是基于多视图图像重建精确的三维表面。以前基于神经体绘制的方法大多是用 mlp 训练一个完全隐式的模型，这通常需要数小时的训练来处理单个场景。最近的研究探索了显式体积表示，通过记忆具有可学习体素网格的重要信息来加速优化。然而，现有的基于体素的方法往往难以重建细粒度的几何形状，即使与基于 sdf 的体绘制方案相结合也是如此。我们发现这是因为 1)体素网格倾向于打破有利于精细几何学习的颜色几何依赖;2)约束不足的体素网格缺乏空间一致性，容易受到局部极小值的影响。在这项工作中，我们提出了 Voxurf，一种基于体素的表面重建方法，既高效又准确。Voxurf 通过几个关键设计解决了上述问题，包括 1)一个两阶段的训练过程，获得连贯的粗形状并连续恢复精细细节，2)一个保持颜色几何依赖性的双色网络，以及 3)一个分层几何特征，以鼓励信息跨体素传播。大量的实验表明，Voxurf 同时实现了高效率和高质量。在 DTU 基准测试中，与之前的全隐式方法相比，Voxurf 以 20 倍的训练加速实现了更高的重建质量。

Introduction

基于多视图图像的神经表面重建 + 完全隐式 MLP
近年来，基于多视图图像的神经表面重建取得了巨大进展。受 Neural Radiance Fields (NeRF) (Mildenhall et al.， 2020)在 Novel View Synthesis (NVS)上的成功启发，最近的作品遵循神经体渲染方案，通过完全隐式模型(Oechsle et al.， 2021)使用有符号距离函数(SDF)或占用场表示 3D 几何形状。Yariv 等，2021;Wang 等人，2021)。这些方法训练了一个深度多层感知器(MLP)，它在每个相机光线上采集数百个采样点，并输出相应的颜色和几何信息。然后通过测量每条光线上累积的颜色与地面真实值之间的差异来应用逐像素监督。使用纯基于 mlp 的框架学习所有几何和颜色细节，这些方法需要对单个场景进行数小时的训练，这大大限制了它们在现实世界中的应用。

NeRF 显示体积方法
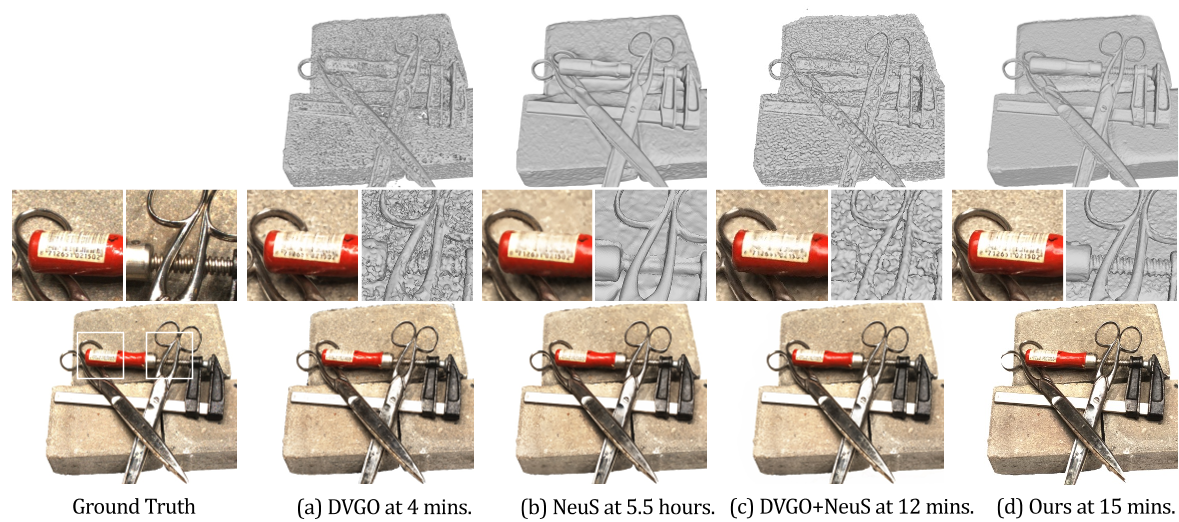
NeRF 的最新进展借助显式体积表示加速了训练过程(Sun et al.， 2022a;Yu et al.， 2022a;Chen et al.， 2022)。这些作品通过显式体素网格直接存储和优化几何和颜色信息。例如，查询点的密度可以很容易地从八个相邻点中插值出来，并且与视图相关的颜色要么用球面谐波系数表示(Yu 等人，2022a)，要么用将可学习的网格特征作为辅助输入的浅 mlp 预测(Sun 等人，2022a)。这些方法以更低的训练成本(< 20 分钟)获得具有竞争力的渲染性能。然而，它们的三维表面重建结果不能忠实地反映精确的几何形状，存在明显的噪声和孔洞(图 1 (a))。这是由于基于密度的体绘制方案固有的模糊性，而明确的体表示引入了额外的挑战。

本文 Voxurf
在这项工作中，我们的目标是利用显式体积表示进行有效的训练，并提出定制设计来获得高质量的表面重建。为此，一个简单的想法是嵌入基于 sdf 的体绘制方案(Wang et al.， 2021;Yariv 等人，2021)将其转化为明确的体积表示框架(Sun 等人，2022a)。然而，我们发现这个 naive 基线模型不能很好地工作，因为它丢失了大部分几何细节并产生了不希望的噪声(图 1 (c))。我们揭示了这个框架的几个关键问题如下。

• 首先，在完全隐式模型中，颜色网络将表面法线作为输入，有效地建立颜色几何依赖关系，促进精细几何学习。然而，在基线模型中，颜色网络倾向于更多地依赖于额外的欠约束体素特征网格输入，从而打破了颜色几何依赖性。
• 其次，由于优化体素网格的自由度很高，如果没有额外的约束，很难保持全局一致的形状。每个体素点的单独优化阻碍了整个体素网格的信息共享，这损害了表面的平滑性并引入了局部最小值。

为了应对挑战，我们引入了 Voxurf，这是一种高效的基于体素的精确表面重建管道:
1)我们利用两阶段的训练过程，获得连贯的粗形状并连续恢复精细细节。
2)我们设计了一个双色网络，它能够通过体素网格表示复杂的颜色场，并与协同工作的两个子网络保持颜色几何依赖性。
3)我们还提出了基于 SDF 体素网格的分层几何特征，以促进更大区域的信息共享，从而实现稳定的优化。
4)我们引入了几个有效的正则化项来提高平滑性和降低噪声。

具体实施+更好的结果
我们对 DTU (Jensen et al.， 2014)和 BlendedMVS (Yao et al.， 2020)数据集进行了实验，以进行定量和定性评估。实验结果表明，Voxurf 在 DTU (Jensen et al.， 2014)基准上实现了比竞争性全隐式方法 news (Wang et al.， 2021)更低的倒角距离，加速速度约为 20 倍。在 NVS 的辅助任务上也取得了显著的效果。如图 1 所示，与之前的方法相比，我们的方法在几何重建和图像渲染中都具有保留高频细节的优势。综上所述，我们的贡献如下:

• 与 SOTA 方法相比，我们的方法使训练速度提高了约 20 倍，在单个 Nvidia A100 GPU 上将训练时间从 5 个多小时减少到 15 分钟。
• 我们的方法实现了更高的表面重建保真度和新颖的视图合成质量，与以前的方法相比，在表面恢复和图像渲染方面都具有更好的细节表现。
• 我们的研究为表面重建的显式体表示框架的架构设计提供了深刻的观察和分析。

Related Work

Multi-view 3D reconstruction
最近，通过神经网络编码 3D 场景的几何形状和外观的隐式表示引起了人们的关注(Park 等人，2019;Chen & Zhang, 2019;Lombardi 等人，2019;Mescheder 等人，2019;Sitzmann et al.， 2019b;Saito 等人，2019;Atzmon 等人，2019;Jiang et al.， 2020;Zhang et al.， 2021;Toussaint et al.， 2022)。
其中，大量的论文探讨了从多视图图像中重建神经表面。基于表面渲染的方法(Niemeyer et al.， 2020;Yariv 等，2020;刘等，2020b;Kellnhofer et al.， 2021)将光线与表面交点的颜色作为最终渲染的颜色，同时要求精确的对象蒙版和仔细的权重初始化。
最近的研究方法(Wang et al.， 2021;Yariv 等，2021;Oechsle 等人，2021;Darmon et al.， 2022;Zhang et al.， 2022;刘等，2020a;Sitzmann et al.， 2019a)基于体绘制(Max, 1995)在统一模型中制定了辐射场和隐式表面表示，从而实现了两种技术的优点。
然而，在纯 MLP 网络中对整个场景进行编码需要很长的训练时间。与这些作品不同，我们利用可学习的体素网格和浅颜色网络进行快速收敛，并在表面和渲染图像中追求精细细节。

Explicit volumetric representation
尽管隐式神经表征在 3D 建模中取得了成功，但最近的进展已经集成了显式 3D 表征，例如点云、体素和 MPIs (Mildenhall 等人，2019)，并受到越来越多的关注(Wizadwongsa 等人，2021;Xu et al.， 2022;Lombardi 等人，2019;Wang et al.， 2022;Fang 等人，2022)。
Instant-ngp 使用多分辨率哈希进行高效编码，并实现了完全融合的 CUDA 内核。
Plenoxels (Yu et al.， 2022a)将场景表示为具有球面谐波的稀疏 3D 网格，其优化速度比 NeRF (Mildenhall et al.， 2020)快两个数量级。
TensoRF (Chen et al.， 2022)将全体积场视为 4D 张量，并将其分解为多个紧凑的低秩张量分量以提高效率。
与我们最相关的方法是 DVGO (Sun et al.， 2022a)，它采用混合架构设计，包括体素网格和浅 MLP。尽管它们在新视图合成方面取得了显著的成果，但它们都不是为了忠实地重建场景的几何形状而设计的。相比之下，我们的目标不仅是从新颖的视点绘制逼真的图像，而且还重建具有精细细节的高质量表面。

PRELIMINARIES

Volume rendering with SDF representation: NeuS
Eq1,2
$\hat{C}(r)=\sum_{i=1}^NT_i\alpha_ic_i,T_i=\prod_{j=1}^{i-1}(1-\alpha_j),$
$\alpha_i=\max\left(\frac{\Phi_s(f(p(t_i)))-\Phi_s(f(p(t_{i+1})))}{\Phi_s(f(p(t_i)))},0\right)$

Explicit volumetric representation: DVGO
Eq3,4
$\sigma=\operatorname{interp}(p,V^{(density)}),$ 三线性插值
$c=\mathrm{MLP}_{\Theta}(\mathrm{interp}(p,V^{(feat)}),p,v),$

Naive 组合。这两种技术的直接结合是用基于 sdf 的体绘制方案取代 DVGO 中的体绘制，如 Eqn. 1 和 Eqn. 2 所示。在这项工作中，它作为 naive 基线，很难产生令人满意的结果，如图 1 (c)所示。在下一节中，我们将通过实证研究来阐明这一现象。

STUDY ON ARCHITECTURE DESIGN FOR GEOMETRY LEARNING

几何学习的结构设计研究

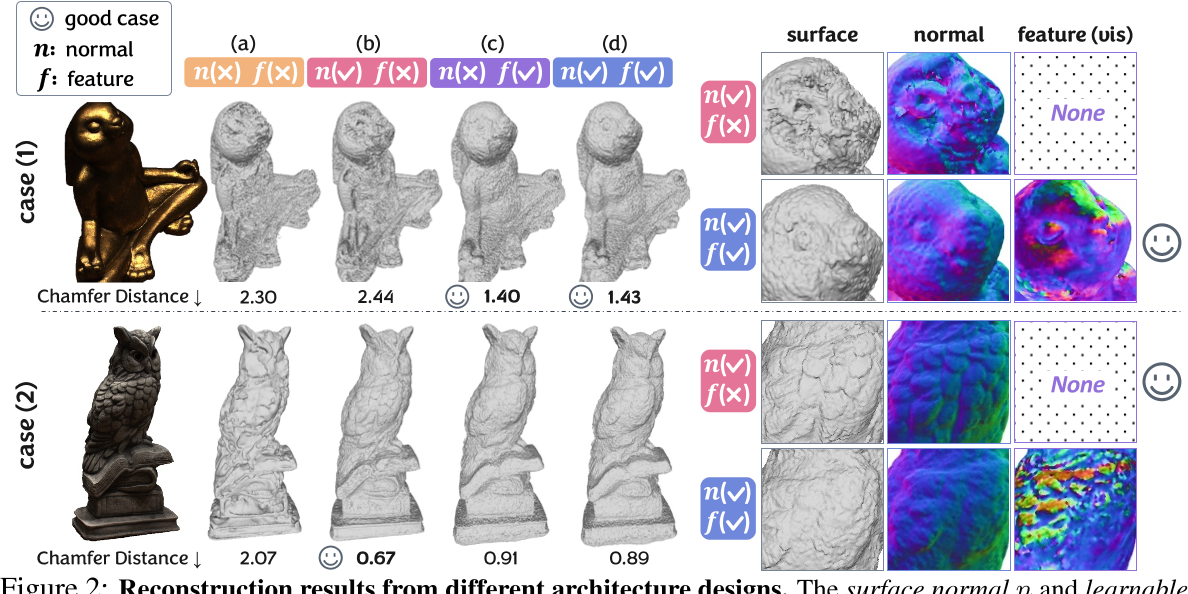
在本节中，我们对基线模型的变体进行了一些先前的实验，旨在找出本任务中架构设计的关键因素。具体来说，我们使用一个 SDF 体素网格 V (SDF)，并应用 Eqn. 2 进行α计算，手动定义 s 的调度。我们从一个浅 MLP 作为颜色网络开始，其中 1)从 $V^{(feat)}$ 插值的局部特征 f 和 2) $V^{(sdf)}$ 计算的法向量 n 都是可选的输入。良好的表面重建应具有连贯的粗结构、精确的精细细节和光滑的表面。接下来我们将关注这些因素，并分析不同架构设计的影响。

The key to maintaining a coherent coarse shape.
直观上，浅层 MLP 的容量是有限的，它很难表示具有不同材质、高频纹理和视依赖光照信息的复杂场景。当 ground truth 图像遇到快速的颜色移动时，在未拟合的颜色场上进行体绘制集成会导致几何结构损坏，如图 2 案例(1)(a)和(b)所示。结合局部特征 f 可以实现快速的颜色学习并提高网络的表示能力，并且问题得到明显缓解，如图 2 案例(1)所示，(a)和(c)， (b)和(d)之间的差异。

The key to reconstructing accurate geometry details.
然后，我们在图 2 中引入另一种情况(2)。它的纹理变化适度，由于漫反射，颜色与表面法线主要相关。尽管在图 2 情形(2)(a)中，在没有法向 n 或特征 fas 输入的情况下，几何图形仍然会崩溃，但在图 2 情形(2)(b)中，即使只有 n 作为输入，我们也可以观察到一些几何细节的合理重构。加入特征 f 不会进一步减小倒角距离(CD);相反，由于可学习特征干扰了几何-颜色依赖关系，即颜色与表面法线之间建立的关系，如图 2 案例(2)所示，(b)与(d)之间的差异。考虑到可学习局部特征的优缺点，设计一个框架是有价值的，利用它来实现一致的形状，并保持颜色-几何依赖于精细的细节。

作者观点：局部特征利于得到连贯的粗结构，但同时也会破坏颜色与表面法线之间的关系，导致精确的细节被破坏

The reason for noisy surfaces.
对于上述所有情况，结果都受到表面明显噪声的影响。与全局学习隐式表示相比，约束不足的体素网格缺乏空间一致性，容易受到局部极小值的影响，从而损害了表面的连续性和光滑性。一个直观的想法是利用来自一个区域而不是局部点的几何线索，这可以引入模型输入、网络组件和损失函数中

METHODOLOGY

受第 4 节中揭示的见解的启发，我们提出了几个关键设计:
1)我们采用两阶段训练程序，依次获得连贯的粗形状(第 5.1 节)和恢复精细细节(第 5.2 节);
2)提出了一种双颜色网络，以保持颜色几何依赖性，恢复精确表面和新视图图像;
3)设计分层几何特征，促进信息跨体素传播，实现稳定优化;
4)我们还引入了平滑先验，包括梯度平滑损失，以获得更好的视觉质量(第 5.3 节)。

COARSE SHAPE INITIALIZATION

我们初始化我们的 SDF 体素网格 $V^{(sdf)}$，在一个准备好的区域内使用椭球状零水平集进行重建，然后，我们在第 4 节中介绍的 $V^{(feat)}$ 的帮助下执行粗形状优化。具体来说，我们用法向量 n 和局部特征 f 作为输入，以及嵌入的位置和观看方向 V 来训练一个浅 MLP，为了促进稳定的训练过程和光滑的表面，我们建议在光滑的体素网格上进行插值，而不是 $V^{(sdf)}$ 的原始数据。

$\mathcal{G}(V,k_g,\sigma_g)$ 表示用高斯核对体素网格 V 进行三维卷积，权重矩阵遵循高斯分布：
$K_{i,j,k}~=~1/Z~\times \exp\left(-((\mathrm{i}-\lfloor\mathrm{k}_\mathrm{g}/2\rfloor)^2+(\mathrm{j}-\lfloor\mathrm{k}_\mathrm{g}/2\rfloor)^2+(\mathrm{k}-\lfloor\mathrm{k}_\mathrm{g}/2\rfloor)^2)/2\sigma_\mathrm{g}^2\right),\mathrm{i},\mathrm{j},\mathrm{k}\in\{0,1,…,\mathrm{k}_\mathrm{g}-1\},$
其中 Z 表示归一化项，$k_g$ 表示核大小，$σ_g$ 表示标准差。因此，查询任意点 p 的光滑 SDF 值 $d ‘$ 变为: $d^{\prime}=\mathrm{interp}(p,\mathcal{G}(V^{(sdf)},k_{g},\sigma_{g})).$

我们在 following Eqn1,2使用 $d ‘$ 进行射线行进积分，并计算重建损失。我们还应用了几个平滑先验，如第 5.3 节所述

FINE GEOMETRY OPTIMIZATION

在此阶段，我们的目标是在粗初始化的基础上恢复精确的几何细节。我们注意到挑战是双重的:
1) 第 4 节的研究揭示了特征体素网格引入的权衡，即以牺牲颜色几何依赖性为代价提高了颜色场的表示能力。
2) SDF 体素网格的优化是基于三线插值来查询三维点。该操作带来了快速收敛，但也限制了不同位置之间的信息共享，这可能导致退化解的局部最小值和次优平滑度。我们提出了一种双色网络和一种分层几何特征来分别解决这两个问题。

Dual color network.

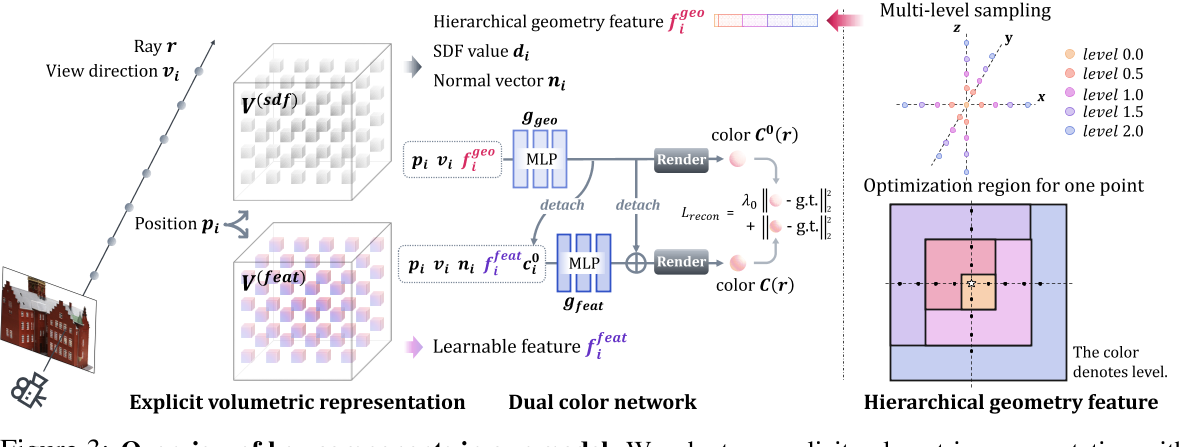
第4节的观察鼓励我们设计一个双色网络，利用从可学习的特征体素网格 $V^{(feat)}$ 插值的局部特征 $f_i^{feat}$，而不失去颜色几何依赖性。如图 3 所示，除了嵌入位置和视图方向外，我们还训练了两个具有不同附加输入的浅 mlp。第一个 MLPggeo 采用 geo 的分层几何特征(稍后将介绍)来构建颜色几何依赖;第二种方法同时采用简单的几何特征(即表面法线 ni)和局部特征 f I 作为输入，以实现更快、更精确的颜色学习，这反过来又有利于几何优化。这两个网络通过分离操作以残差方式组合:在输入 togf 之前分离 ggeo 的输出，表示为 c0，并将输出添加回 c0 的分离副本，以获得最终的颜色预测 c

第4节的观察结果鼓励我们设计一个双色网络，利用从可学习的特征体素网格 $V^{(feat)}$ 插值的局部特征 $f_i^{feat}$，而不失去颜色几何依赖性。如图3所示，除了嵌入位置和视图方向外，我们还训练了两个具有不同附加输入的浅 mlp。第一个 MLP $g_{geo}$ 采用分层几何特征 $f_i^{geo}$ (稍后将介绍)来构建 color-geometry 依赖关系;第二个 MLP $g_{feat}$ 同时使用一个简单的几何特征 (即表面法线 $n_i)$ 和局部特征 $f_i^{feat}$ 作为输入，以实现更快，更精确的颜色学习，从而有利于几何优化。这两个网络通过分离操作以残差方式组合在一起: $g_{geo}$ 的输出(表示为 $c_0$)在输入 $g_{feat}$ 之前被分离，然后将输出添加回 $c_{0}$ 的分离副本，以获得最终的颜色预测 $c$。

$g_{geo}$ 和 $g_{feat}$ 的输出都由地面真值图像和沿射线的集成颜色之间的重建损失来监督。具体来说，将它们的渲染颜色表示为 $C^0(r)$ 和 $C(r)$，整体重构损失表示为:
$\mathcal{L}_{recon}=\frac1{\mathcal{R}}\sum_{r\in\mathcal{R}}\left(||C(r)-\hat{C}(r)||_2^2+\lambda_0||C_0(r)-\hat{C}(r)||_2^2\right),$

式中 $\hat{C}(r)$ 表示真色，$\lambda_{0}$ 表示损失权值。$V^{(feat)}$ 和 MLP $g_{feat}$ 对场景的拟合速度较快，而 MLP $g_{geo}$ 对场景的拟合速度相对较慢。分离操作促进了 $g_{geo}$ 在自身重构损失的指导下的稳定优化，这有助于保持颜色几何依赖性。

Hierarchical geometry feature.

分层几何特征。使用表面法线 $n$ 作为颜色网络的几何特征是一个简单的选择，而它只从相邻的 $V^{(SDF)}$ 的网格中获取信息。为了扩大感知区域并鼓励信息跨体素传播，我们建议查看更大的 SDF 场区域，并将相应的 SDF 值和梯度作为颜色网络的辅助条件。具体来说，对于给定的 3D 位置 $p=(x,y,z)$，我们取体素大小 $v_s$ 的一半作为步长，并沿着 $x,y,z$ 坐标轴两侧定义它的邻居。以 X 轴为例,邻近的坐标定义为 $p_x ^ {l -} = (x ^ {l -}, y, z)$ 和 $p_x ^ {l +} = (x ^ {l +}, y, z)$,在 $X ^ {l -} = \max(x-l v_s, 0)$, $X ^ {l +} = \min (x + l v_s ,v_x ^ m), l \in[0.5, 1.0, 1.5,…]$ 表示相邻区域的“水平”，$v_x^m$ 表示体素网格在 $x$ 轴上的最大值。然后，我们通过将不同级别的邻居连接在一起，将定义扩展为分层方式，如下所示:
$\begin{aligned}d_k^l=[d_k^{l-},d_k^{l+}]&=[\text{interp}(p_k^{l-},V^{(sdf)}),\text{interp}(p_k^{l+},V^{(sdf)})],k\in\{x,y,z\},\\f_p^{sdf}(l)&=[d^0,d_x^{0.5},d_y^{0.5},d_z^{0.5},\cdots,d_x^{l},d_y^{l},d_z^{l}]^T,\end{aligned}$

其中 $d_x^l$ 表示在 $p_x^{l-}$ 和 $p_x^{l+}$ 位置从 $V^{(SDF)}$ 查询到的 SDF 值。当 $l= 0$ 时，f $_p^{sdf}(0) = d^0$，这正是位置 $p$ 本身的 sdf 值。然后，我们还将梯度信息合并到几何特征中。具体来说，我们可以得到梯度向量 $\delta_x^l=(d_x^{l+}-d_x^{l-})/(2lv_s)$。我们将 $[\delta_x^l，\delta_y^l，\delta_z^l]$ 归一化为 l 的 l2 范数，表示为 $n^l\in\mathbb{R}^3。$ normal 的分层版本公式为: $\begin{aligned}f_p^{normal}(l)=[n^{0.5},\cdots,n^l].\end{aligned}$
最后，在点 p 处的分层几何特征为预定义的水平 $l\in[0.5,1.0,1.5，…]$ 是 $f_p^{geo}(l)=[f_p^{sdf}(l),f_p^{normal}(l)].$，将 $f_p^{geo}(l)$ 输入进 MLP $g_{geo}$ 中辅助几何学习

SMOOTHNESS PRIORS

我们结合了两个有效的正则化项来提高训练过程中的表面平滑度。
(1)首先，我们采用了总变分(TV)正则化(Rudin & Osher, 1994):
$\mathcal{L}_{TV}(V)=\sum_{d\in[D]}\sqrt{\Delta_{x}^{2}(V,d)+\Delta_{y}^{2}(V,d)+\Delta_{z}^{2}(V,d)},$
其中 $\Delta_x^2(V,d)$ 表示 voxel $v:=(i;j;k)$ 和 voxel $(i+1;j;k)$ 中第 d 通道值之间的平方差，可以类似地扩展到 $\Delta_y^2(V,d)$ 和 $\Delta_z^2(V,d)$。我们将上面的 TV 项应用于 SDF 体素网格，表示为 $\mathcal{L}_{TV}(V^{(SDF)})$，这鼓励了连续和紧凑的几何结构。

(2)我们也假设表面在局部区域是光滑的，我们遵循第 5.1 节中高斯卷积的定义，引入光滑正则化，公式为:
$\mathcal{L}_{smooth}(V)=||\mathcal{G}(V,k_{g},\sigma_{g})-V||_{2}^{2},$
我们将上述平滑项应用于 SDF 体素网格的梯度，得到梯度平滑损失，记为 $\mathcal{L}_{smooth}(\nabla V^{(sdf)})$。它鼓励光滑的表面，减轻了自由空间中嘈杂点的问题。注意，由于 SDF 的显式表示，我们也可以在训练后自然地对 SDF 字段进行后处理。例如，在提取几何图形之前应用高斯核可以进一步提高表面的平滑度，从而获得更好的可视化效果。

最后，将整体训练损失表示为: $\mathcal{L}=\mathcal{L}_{recon}+\lambda_{tv}\mathcal{L}_{TV}(V^{(sdf)})+\lambda_{s}\mathcal{L}_{smooth}(\nabla V^{(sdf)}),$

EXPERIMENTS

使用 DTU 数据集定性定量的比较，再 BlenderMVS 数据集上定性的比较
比较的方法：IDR、NeuS、NeRF、DVGO、Point-NeRF，为所有方法提供了一个干净的背景，以便公平比较。

CONCLUSION

本文提出了一种基于体素的神经表面重构方法 Voxurf。它包括几个关键设计:两阶段框架获得连贯的粗形状，并依次恢复精细细节;双色网络有助于保持颜色几何依赖性，分层几何特征鼓励信息跨体素传播;有效平滑先验包括梯度平滑损失进一步提高视觉质量。大量的实验表明，Voxurf 同时实现了高效率和高质量。

复现

本机：只能使用 cuda11.1 版本

• Win10，torchvision 0.11.0+cu111 没有 windows 版本
  • 换 cu113 版本
• Wsl2，ubuntu 版本无法使用 cuda11.1

作者没有做好多版本 torch 和 cuda 的适配