| Title | DiffuStereo: High Quality Human Reconstruction via Diffusion-based Stereo Using Sparse Cameras |
|---|---|
| Author | Ruizhi Shao, Zerong Zheng, Hongwen Zhang, Jingxiang Sun, Yebin Liu |
| Conf/Jour | ECCV 2022 Oral |
| Year | 2022 |
| Project | DiffuStereo Project Page (liuyebin.com) |
| Paper | DiffuStereo: High Quality Human Reconstruction via Diffusion-based Stereo Using Sparse Cameras (readpaper.com) |
THUman2.0数据集demo结果好(除手、脸和脚),训练代码还未开源
Abstract
我们提出了 DiffuStereo,这是一种仅使用稀疏相机(本工作中有 8 个)进行高质量 3D 人体重建的新系统。其核心是一种新型的基于扩散的立体模型,将扩散模型这一功能强大的生成模型引入到迭代立体匹配网络中。为此,我们设计了一个新的扩散核和附加的立体约束来促进网络中的立体匹配和深度估计。我们进一步提出了一个多级立体网络架构来处理高分辨率(高达 4k)的输入,而不需要负担得起的内存占用。给定一组稀疏视图彩色人体图像,基于多层次扩散的立体网络可以生成高精度的深度图,然后通过高效的多视图融合策略将深度图转换为高质量的三维人体模型。总的来说,我们的方法可以自动重建人体模型,其质量与高端密集视角相机平台相当,这是使用更轻的硬件设置实现的。实验表明,我们的方法在定性和定量上都大大优于最先进的方法。
Introduction
贡献:
1)我们提出了 DiffuStereo,这是一个轻量级和高质量的系统,用于稀疏多视图相机下的人体体积重建。
2)据我们所知,我们提出了第一个将扩散模型引入立体和人体重建的方法。我们通过精心设计一个新的扩散核并在扩散条件中引入额外的立体约束来扩展香草扩散模型。
3)我们提出了一种新的多层次扩散立体网络,以实现准确和高质量的人体深度估计。我们的网络可以优雅地处理高分辨率(高达 4k)图像,而不会遭受内存过载的困扰。
Method

DiffuStereo 可以从稀疏的(少至 8 个)摄像机中重建高质量的人体模型(所有摄像机均匀分布在目标人周围的一个环上)。这种稀疏的设置给高质量的重建带来了巨大的挑战,因为两个相邻视图之间的角度可以大到 45 度。DiffuStereo 通过一种现成的重建方法 DoubleField[52]、一种基于扩散的立体网络和一种轻量级多视图融合模块的共同努力,解决了这些挑战。
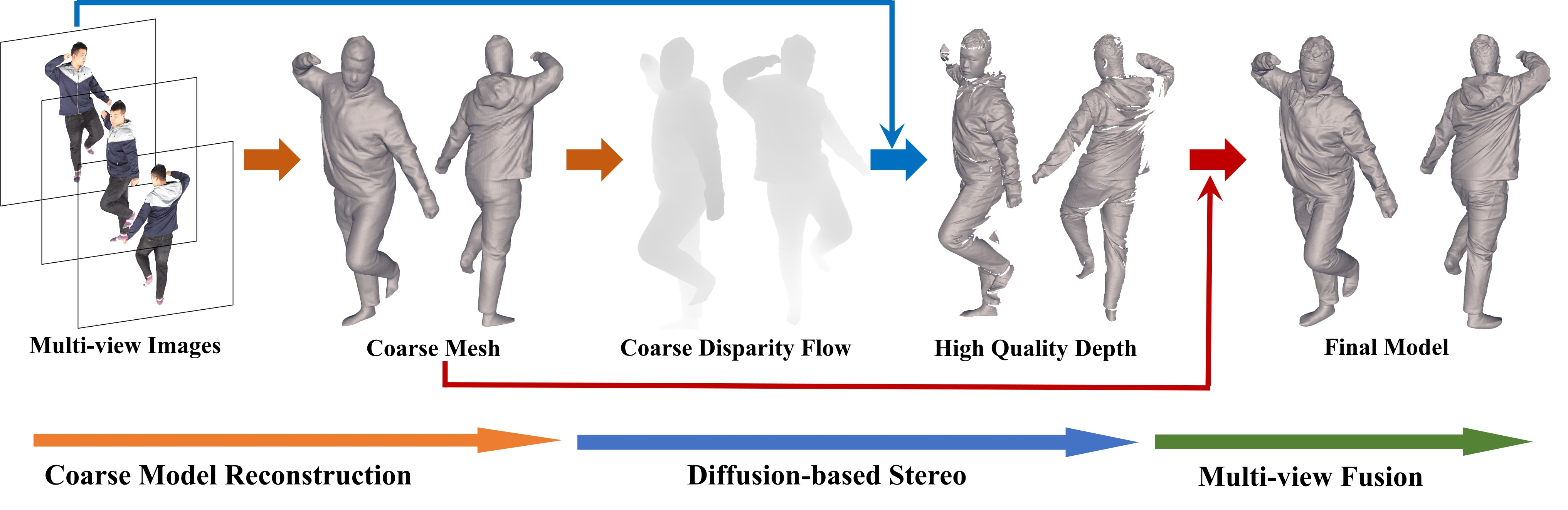
DiffuStereo 系统由三个关键步骤组成:
- 通过 DoubleField[52]预测初始人体网格,并渲染为粗视差流(第 3.1 节); 作者先前提出的 DoubleField,最新的最先进的人体重建方法之一,表面和辐射场被桥接以利用人体几何先验和多视图外观,在给定稀疏视图输入的情况下提供良好的网格初始化。
- 对于每两个相邻视图,在基于扩散的立体中对粗视差图进行细化,得到高质量的深度图(第 3.2 节);基于扩散的立体网络对每个输入视图的视差图有很强的改进能力,其中使用扩散过程进行连续的视差细化。
- 初始的人体网格和高质量的深度图被融合成最终的高质量人体网格(第 3.3 节),其中一个轻量级的多视图融合模块以初始网格作为锚点位置,有效地组装了部分精细的深度图。
Mesh, Depth, Disparity Initialization
DoubleField 得到初始人体 mesh,然后渲染为深度图
m 和 n 是两个相邻视图的索引,为了得到视图 m 到相邻视图 n 的粗视差图 $x_{c}$,取视图 m 的深度图 $D^m_c$,计算像素位置 o = (i, j)处的视差: $\mathbf{x}_c(\boldsymbol{o})=\pi^n\left((\pi^m)^{-1}\left([\boldsymbol{o},\mathbf{D}_c^m(\boldsymbol{o})]^\mathrm{T}\right)\right)-\boldsymbol{o}$ Eqn.1
其中 $(\pi^{m})^{-1}$ 将深度图 $D^m_c$ 中的点变换为世界坐标系,$π^n$ 将世界坐标系中的点投影为图像坐标系。
由于初始视差图是从粗糙的人体网格中计算的,因此可以在很大程度上缓解大位移和遮挡区域的问题。正如即将介绍的那样,这些视差图通过 Diffusion-based Stereo 进一步细化,以获得每个输入视点的高质量深度图
Diffusion-based Stereo for Disparity Refinement
现有的(stereo methods)立体方法 63MVSNet: Depth Inference for Unstructured Multi-view Stereo (readpaper.com) [9、20、23、68、33、63、69、70]采用 3D/4D 成本体离散预测视差图,难以实现亚像素级的流量 flow 估计。为了克服这一限制,我们提出了一种基于扩散的立体网络,使立体网络可以在迭代过程中学习连续流。
具体来说,我们的基于扩散的立体图像包含一个正演过程和一个反演过程,以获得最终的高质量视差图。在正演过程中,将初始视差图扩散到有噪声分布的图中。在反向的过程中,在具有多个立体相关特征的条件下,从噪声图中恢复出高质量的视差图。
下面,我们简要介绍了一般的扩散模型,然后介绍了我们将扩散模型的连续性与基于学习的迭代立体相结合的解决方案。此外,我们还提出了一个多层次的网络结构,以解决高分辨率图像输入的内存问题。
Generic Diffusion Model
More formally, the diffusion model can be written as two Markov Chains:
Eqn.2,3,4
其中 $q(\mathbf{y}_{1:T}|\mathbf{y}_{0})$ 为正向函数,$q(\mathbf{y}_t|\mathbf{y}_{t-1})$ 为扩散核,表示加入噪声的方式,$\mathcal{N}$ 为正态分布,I 是 the identical matrix,pθ()为反向函数,采用去噪网络 $\mathcal{F}_θ$ 对 $y_t$ 进行去噪,为附加条件。当 T→∞时,正反过程可以看作是连续过程或随机微分方程[55],这是连续 flows 估计的自然形式。正如之前的工作[55]所验证的那样,在参数更新中注入高斯噪声使迭代过程更加连续,并且可以避免陷入局部极小。在这项工作中,我们将展示,这样一个强大的生成工具也可以用来为以人为中心的立体任务产生连续的 flows。
与一般的扩散模型相比,我们的 diffusion-based stereo 采用了两种特定于任务的设计:
I)考虑到 stereo flow estimation 不是纯粹的生成任务,采用了一种新的扩散核;
Ii)反向过程中涉及与立体相关的特征和监督,以确保颜色的一致性和极线约束 epipolar constraints.。
Disparity Forward Process
本文扩散模型的输入 $\mathbf{y}_{0}$ 是地面真实视差图 $\mathbf{\hat{x}}$ 和粗视差图 $x_c$ 之间的残差视差 $\mathbf{\hat{y}}_0$,即 $\mathbf{\hat{y}}_0=\hat{\mathbf{x}}-\mathbf{x}_c$。
与现有的图像合成生成扩散模型利用 $\sqrt{1-\beta_t}$ 逐步减小 $\mathbf{y}_{t-1}$ 的尺度不同,我们设计了一个扩散核来保持 $\mathbf{y}_{t-1}$ 的尺度,线性漂移 $\mathbf{y}_{0}$ 到 $\mathbf{y}_{t}$,即 Eqn(3) 改写为:Eqn.5
$q(\mathbf{y}_{t}|\mathbf{y}_{t-1})=\mathcal{N}(\mathbf{y}_{t}|\mathbf{y}_{t-1}-\alpha_{t}\mathbf{y}_{0},\alpha_{t}\mathbf{I}),$
其中 $α_t$ 是缩放噪声的参数。基于这种新的扩散核,视差正向过程使用 Eqn(2) 和 (5)逐渐向地面真实残差视差 $\mathbf{\hat{y}}_0$ 添加噪声。在我们的实验中,我们发现我们的扩散内核使反向过程更加稳定,并且在推理时有效地减少了所需的迭代步数。我们新内核下的前向过程的推导与[24]相似,可以在 Supp 中找到
Stereo-conditioned Reverse Process.
Eqn.4
$p_{\theta}(\mathbf{y}_{0:T}|\mathbf{s}) =p(\mathbf{y}_T)\prod_{t=1}^Tp_\theta(\mathbf{y}_{t-1}|\mathbf{y}_t,\mathbf{s})$
基于扩散的立体的反向过程旨在利用 Eqn(4)从噪声 $\mathbf{y}_T$ 中恢复残差视差 $\mathbf{\hat{y}}_0$。在这个过程中,扩散立体网络充当 Eqn(4)中的去噪网络 $\mathcal{F}_θ$ 。通过将 $\mathbf{y}_{t}$ 和 s 作为输入并预测 $\widetilde{\mathbf{y}}_0.$。
由于扩散核也会影响反向过程,我们网络的去噪过程与我们的新核下的泛型去噪过程不同。给定方程式 5 中的内核,反向过程中每一步的公式可以写成:$p_{\theta}(\mathbf{y}_{t-1}|\mathbf{y}_{t},\mathbf{s})=\mathcal{N}(\mathbf{y}_{t-1}|\mu_{\theta}(\mathbf{y}_{t},\gamma_{t},\mathbf{s}),\sigma_{t}^{2}\mathbf{I}),$ Eqn.6
其中 $\gamma_{t}=\sum_{i=1}^{t}\alpha_{i},\sigma_{t}^{2}=\frac{\alpha_{t}\gamma_{t-1}}{\gamma_{t}},\mathrm{and}\mu_{\theta}()$ 为去噪网络 $\mathcal{F}_θ$ 的预测过程。此外,我们将预测的 $\widetilde{\mathbf{y}}_0$ 代入 $q(\mathbf{y}_{t-1}|\mathbf{y}_t,\mathbf{y}_0)$ 的后验分布,表示 $p_\theta(\mathbf{y}_{t-1}|\mathbf{y}_t)$ 的均值: $\mu_{\theta}(\mathbf{y}_{t},\gamma_{t},\mathbf{s})=\frac{\alpha_{t}}{\gamma_{t}}\widetilde{\mathbf{y}}_{0}+\frac{\gamma_{t-1}}{\gamma_{t}}\mathbf{y}_{t}.$ Eqn.7
the whole reverse process:$\mathbf{y}_{t-1}\leftarrow\frac{\alpha_{t}}{\gamma_{t}}\widetilde{\mathbf{y}}_{0}+\frac{\gamma_{t-1}}{\gamma_{t}}\mathbf{y}_{t}+\frac{\alpha_{t}\gamma_{t-1}}{\gamma_{t}}\epsilon_{t},\epsilon_{t}\sim\mathcal{N}(\mathbf{0},\mathbf{1}).$ Eqn.8
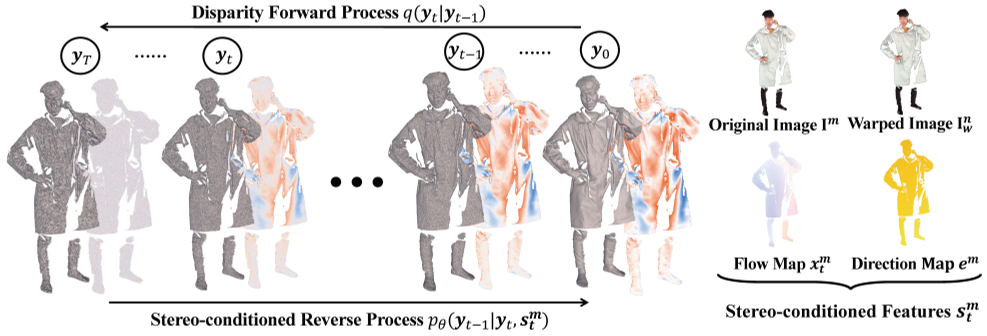
由于视差细化不是完全生成过程,扩散立体网络 $\mathcal{F}_θ$ 以附加条件作为输入来恢复高质量的视差流。在我们的解决方案中,四种类型的立体相关图(图 3 右)充当方程式(4)中的附加条件 s 保证反向过程每一步的颜色一致性和极线约束
- The original image $\mathbf{I}_m$ of the view m;
- The warped image $\mathbf{I}_w^n$ of view n, which is obtained by transforming pixels of $\mathbf{I}^n$ using current flow $\mathbf{x}_t^m=\mathbf{x}^m+\mathbf{y}_t$: $\mathbf{I}_w^n(\boldsymbol{o})=\mathbf{I}^n(\mathbf{x}_t^m(\boldsymbol{o})+\boldsymbol{o}).$
- The current flow map $\mathbf{x}_t^m$ ($\mathbf{x}_t^m=\mathbf{x}^m+\mathbf{y}_t$)
- The direction map $\mathbf{e}^m$ of epipolar line 极线, which is computed as: $\mathbf{e}^m=(\dot{\mathbf{x}}_c^m-\mathbf{x}_c^m)/|\dot{\mathbf{x}}_c^m-\mathbf{x}_c^m|_2,$
- 其中̇ $\dot{\mathbf{x}}_c^m$ 是基于粗深度图 $\mathbf{D}_c^m$ 和固定移位β变换的移位流图: $\dot{\mathbf{x}}_c^m(\boldsymbol{o})=\pi^n((\pi^m)^{-1}([\boldsymbol{o},\mathbf{D}_c^m(\boldsymbol{o})+\beta]^T))-\boldsymbol{o}.$
在上述四种条件下, $\mathbf{I}_m$ 和 $\mathbf{I}_w^n$ 鼓励网络意识到颜色一致性,而 $\mathbf{x}_t^m$ 和 $\mathbf{e}^m$ 提供了关于流向网络的提示以进行更好预测。我们通过将上述立体相关映射连接为 $\mathrm{s}_t^m=\bigoplus(\mathbf{I}^m,\mathbf{I}_w^n,\mathbf{x}_t^m,\mathbf{e}^m).$ 来约束网络。条件 $\mathrm{s}_t^m$ 与 $(\mathbf{y}_t^m,t)$ 进一步串联,并馈入扩散立体网络。此外,我们还将网络输出映射 R 约束为仅一个通道,以便预测的剩余 flow $\widetilde{\mathbf{y}}_t=\mathrm{e}^m\cdot R$ 被迫沿着极线移动。
当反向过程完成时,利用 Eqn(1)的逆公式,将最终流 $\mathbf{x}^m+\widetilde{\mathbf{y}}_0^m$ 转换回视图 m 的精细深度图 $\mathrm{D}_f^m$。
Multi-level Network Structure 解决 memory 问题
对于高质量的人体重建,利用高分辨率输入图像至关重要。当应用上述扩散立体网络时,当采用高分辨率图像(在我们的实验中为4K)作为输入时,会出现内存问题。受 PIFuHD[51]的启发,我们采用多层网络结构来解决这一问题,其中全局网络 $\mathcal{F}_{g}$ 与扩散立体网络 $\mathcal{F}_{\theta}$ 相结合。这样,$\mathcal{F}_{g}$ 和 $\mathcal{F}_{\theta}$ 可以分别在全局和扩散层面产生视差流。
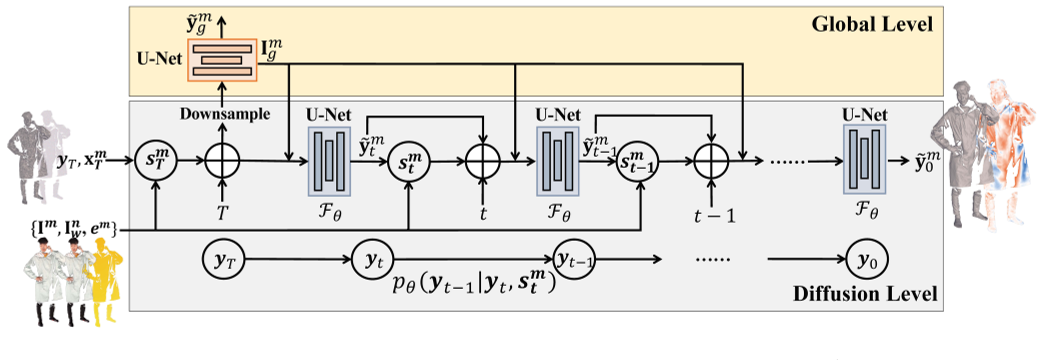
如图4所示,在全局级别上,粗初始流 $\mathrm{x}_c^m$ 和条件立体特征 $s^{m}$ 都被下采样到 512×512 的分辨率,然后被馈送到全局网络 $\mathcal{F}_{g}$ 中。其直接预测低分辨率残差流 $\widetilde{\mathbf{y}}_g^m.$ 注意,全局级别的流量估计不是扩散过程,而是学习包含人类语义信息的全局特征。在扩散级,我们采用来自全局网络的最后图像特征 $\mathbf{I}_g^m$ 作为扩散立体网络的附加条件。因此,本地级网络中的立体相关特征被修改为 $\bigoplus(\mathbf{I}^m,\mathbf{I}_w^n,\mathbf{x}_t^m,\mathbf{e}^m,\mathbf{I}_g^m).$ 得益于多级结构,由于可以以基于补丁的方式训练扩散立体网络,因此可以在很大程度上克服内存问题。此外,在全局特征 $\mathbf{I}_g^m$ 的指导下,我们的扩散立体网络可以更加专注于精细细节的恢复。
Training of Diffusion-based Stereo
Global Level. 我们将 GT 残差流下采样到512的分辨率,并用全局损失 $\mathcal{L}_g$ 训练全局网络 $\mathcal{F}_{g}$:
$\mathcal{L}_g=\frac{1}{HW}\sum_{i=1}^{H}\sum_{j=1}^{W}|\widetilde{\mathbf{y}}_g(i,j)-\mathbf{y}_0(i,j)|^2,$
全局损失促使网络学习人类语义特征进行流量估计。
Diffusion Level. Follow WaveGrad: Estimating Gradients for Waveform Generation (readpaper.com),我们随机选择一个时间步长 t,并将 GT 残余流 $\mathbf{y}_0$ 扩散到 $\mathbf{y}_t$,生成训练样本,使用: $q(\mathbf{y}_t|\mathbf{y}_0)=\mathcal{N}(\mathbf{y}_t|(1-\gamma_t)\mathbf{y}_0,\gamma_t\mathbf{I}).$
然后在第 t 步采用扩散损失 $\mathcal{L}_{d}=$ 来训练扩散立体网络 $\mathcal{F}_{\theta}$: $\mathcal{L}_{d}=\frac{1}{HW}\sum_{i=1}^{H}\sum_{j=1}^{W}|(\mathcal{F}_{\theta}(\mathbf{y}_{t},\mathbf{s}_{t},t))(i,j)-\mathbf{y}_{0}(i,j)|_{2}^{2}.$
Light-weight Multi-view Fusion
在本节中,我们提出了一种轻量级的多视图混合融合来融合精细的深度图 $\mathbf{D}_{f}^{1},…,\mathbf{D}_{f}^{n}$ 和粗网格 $\mathrm{m}_{c}$ 来重建最终模型。
在融合之前,我们首先使用侵蚀核去除深度边界,并将每个精细的深度图 $\mathbf{D}_f^i$ 转换为一个点云 $\mathbf{p}^{i}=(\pi^i)^{-1}(\mathbf{D}_f^i).$
由于标定误差在实际数据中是不可避免的,因此从多视角估计的精细化深度图可能无法准确对齐。为了解决这个问题,我们利用非刚性 ICP 对深度点云 $\mathrm{p}^{i}$ 和粗网格的点云 $\mathrm{p}^{c}$ 进行对齐,其中粗点云作为后续对齐的锚点模型。在我们的非刚性 ICP 中,优化目标 $\mathcal{L}_{icp}=\mathcal{L}_d+\mathcal{L}_s$ 由数据项 $\mathcal{L}_d$ 和光滑项 $\mathcal{L}_s$ 组成,
$\mathcal{L}_d=\sum_{i=1}^n\sum_{j=i+1}^n\sum_{(a,b)\in\widetilde{\mathbf{N}}^{i,j}}|\widetilde{\mathbf{p}}_a^i-\widetilde{\mathbf{p}}_b^j|^2+\lambda_d\sum_{i=1}^n\sum_{(a,b)\in\widetilde{\mathbf{N}}_c^i}|\widetilde{\mathbf{p}}_a^i-\mathbf{p}_b^c|^2$
$\mathcal{L}_s=\lambda_s\sum_{i=1}^n\sum_{(a,b)\in\mathbf{N_i}}|\widetilde{\mathbf{d}}_a^i-\widetilde{\mathbf{d}}_b^i|^2/|\mathbf{p}_a^i-\mathbf{p}_b^i|^2,$
式中 $\mathbf{d}^{i}$ 为深度点云 $\mathrm{p}^{i}$ 的位移,N 为搜索到的邻域对应关系的集合。我们采用最近邻算法搜索对应,搜索半径的阈值为 2mm。
优化后的最终点云 $p^{f}$ 是优化后的深度点云 ${\tilde{\mathrm{p}}}^{i}$ 与粗点云 $p ^{c}$ 的结合,而最终的网格可由最终点云 $p^{f}$ 使用泊松重建[32]重建。
Experiment
在我们的实现中,我们采用类似于 Diffusion Models Beat GANs on Image Synthesis[12]的 U-Net[47]模型作为全局网络 $\mathcal{F}_{g}$ 和扩散网络 $\mathcal{F}_{\theta}$ 的结构。我们的扩散模型 T 是30,在图像生成任务中比原始模型小得多。关于其他扩散参数,包括$\alpha_t,\gamma_t$ 和更多的实现细节,请参阅补充材料。
Training Data Preparation.
我们从Twindom[57]收集了300个模型,并渲染图像对进行训练。我们首先从360°角度密集渲染4K分辨率的图像和深度图。然后,我们在8个均匀分布视图的图像上运行DoubleField[52],预测分辨率为$512^3$的SDF体积,并使用marching cube进一步检索粗糙的人体网格。在我们的基于扩散的立体网络训练过程中,我们从同一模型的渲染图像中随机选择两个视图,并在[20,50]的间隔内约束它们的角度。我们还计算了两个视图之间的遮挡区域,并过滤掉不好的部分,以避免不稳定的训练。
Evaluation Data Preparation.
我们从THUman2.0[65]数据集中随机选择300个模型进行评估。4K分辨率的人物图像和深度图从360角度渲染。
Discussion
Conclusion.
我们介绍了DiffuStereo,一个从稀疏视图RGB图像重建高质量3D人体模型的新系统。通过对人类模型的初步估计,我们的系统利用基于扩散模型的新型迭代立体网络,从每两个相邻视图生成高精度的深度图。这种基于扩散的立体网络经过精心设计,可以处理稀疏视图、高分辨率输入。高质量的深度图可以组装来生成最终的3D模型。与现有的方法相比,我们的方法可以重建更清晰的几何细节,达到更高的精度。
Limitation.
我们的方法的主要限制是依赖于双场来估计一个初始的人类模型。此外,由于在稀疏视图设置中缺乏观测,我们的方法无法重建不可见区域的几何细节。