QiYun

Note

PlankAssembly

Posted on Edited on In
6.3k 23 mins.
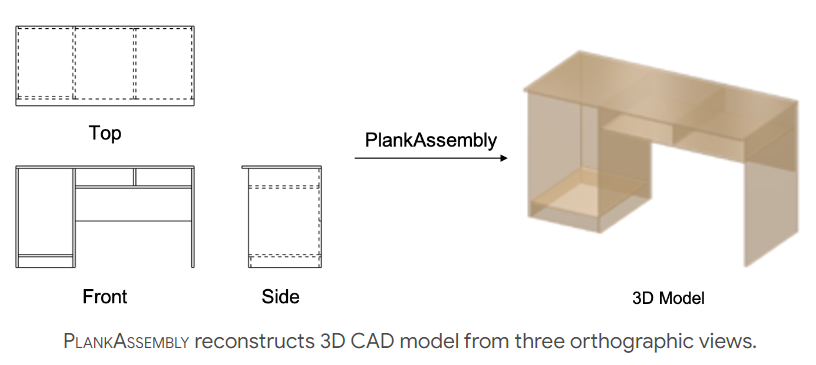
Title PlankAssembly: Robust 3D Reconstruction from Three Orthographic Views with Learnt Shape Programs
Author Wentao Hu Jia Zheng Zixin Zhang Xiaojun Yuan Jian Yin Zihan Zhou
Conf/Jour ICCV
Year 2023
Project PlankAssembly: Robust 3D Reconstruction from Three Orthographic Views with Learnt Shape Programs (manycore-research.github.io)
Paper PlankAssembly: Robust 3D Reconstruction from Three Orthographic Views with Learnt Shape Programs (readpaper.com)

image.png

贡献：

  • 基于Transform的自注意力提出模型，用于将2D的三个orthographic的line drawing转化为3D模型，可以实现从图纸不完美的输入中生成正确的3D模型
  • 输入的三个orthographic图纸被编码，输出的是3D模型程序的编码，最后解码后即3D模型对应的程序DSL

挑战：

  • 应用于无法获得甚至不存在大规模CAD数据的领域，例如建筑物或复杂的机械设备
  • 没有考虑图纸中的符号、图层等信息

Discussion&Conclusion

本文提出了一种基于三个正射影视图的三维CAD模型重建生成方法。从我们的实验中可以学到两个教训lessons:

  • 首先，与寻找2D线条图和3D模型之间的明确对应关系相比，注意机制在深度网络对不完美输入的鲁棒性中起着关键作用。
  • 其次，在生成模型中加入领域知识有利于重构和下游应用

有人可能会说，我们的实验仅限于橱柜家具，这是一种特殊的CAD模型。然而，我们强调我们的主要思想和经验教训是通用的，可以应用于任何CAD模型。例如，DeepCAD[35]等先前的工作已经开发出能够生成适合机械零件的CAD命令序列的神经网络。与橱柜家具不同，机械部件通常具有非矩形轮廓(但块状较少)。因此，将我们的方法扩展到这些领域是相对简单的。

一个更具挑战性的场景是尝试将我们的数据驱动方法应用于无法获得甚至不存在大规模CAD数据的领域，例如建筑物或复杂的机械设备。此外，我们目前的方法没有考虑CAD图纸中可用的其他信息，如图层、文本、符号和注释。近年来，人们提出了几种用于CAD图中全光学符号识别的方法[6,39,5]。我们相信这些信息对于从复杂的CAD图纸进行3D重建也是至关重要的。

AIR

在本文中，我们开发了一种新的方法来自动转换二维线条图从三个正射影到三维CAD模型。
该问题的现有方法通过将2D观测数据反向投影到3D空间来重建3D模型，同时保持输入和输出之间的显式对应。这种方法对输入中的错误和噪声很敏感，因此在实践中经常失败，因为人类设计师创建的输入图纸不完美。
为了克服这一困难，我们利用基于transformer的序列生成模型中的注意机制来学习输入和输出之间的灵活映射。此外，我们还设计了适合生成感兴趣对象的形状程序，以提高重建精度并促进CAD建模应用。
在一个新的基准数据集上的实验表明，当输入有噪声或不完整时，我们的方法明显优于现有的方法。

Introduction

在本文中，我们解决了计算机辅助设计(CAD)中一个长期存在的问题，即从三个正射影视图重建三维物体。在当今的产品设计和制造行业中，设计师通常使用二维工程图纸来实现，更新和分享他们的想法，特别是在初始设计阶段。但为了进一步分析(如有限元分析)和制造，这些2D设计必须在CAD软件中手动实现为3D模型。因此，如果有一种方法可以自动将二维图纸转换为三维模型，将大大简化设计过程，提高整体效率

作为2D绘图中最流行的描述物体的方式，正射影视图是物体在垂直于三个主轴之一的平面上的投影(图1)。在过去的几十年里，从三个正射影视图进行三维重建得到了广泛的研究，在适用对象的类型和计算效率方面有了显著的改进[25,10,19,37,38,28,18,21,8,9]。然而，据我们所知，这些技术并没有在CAD软件和商业产品中得到广泛采用。

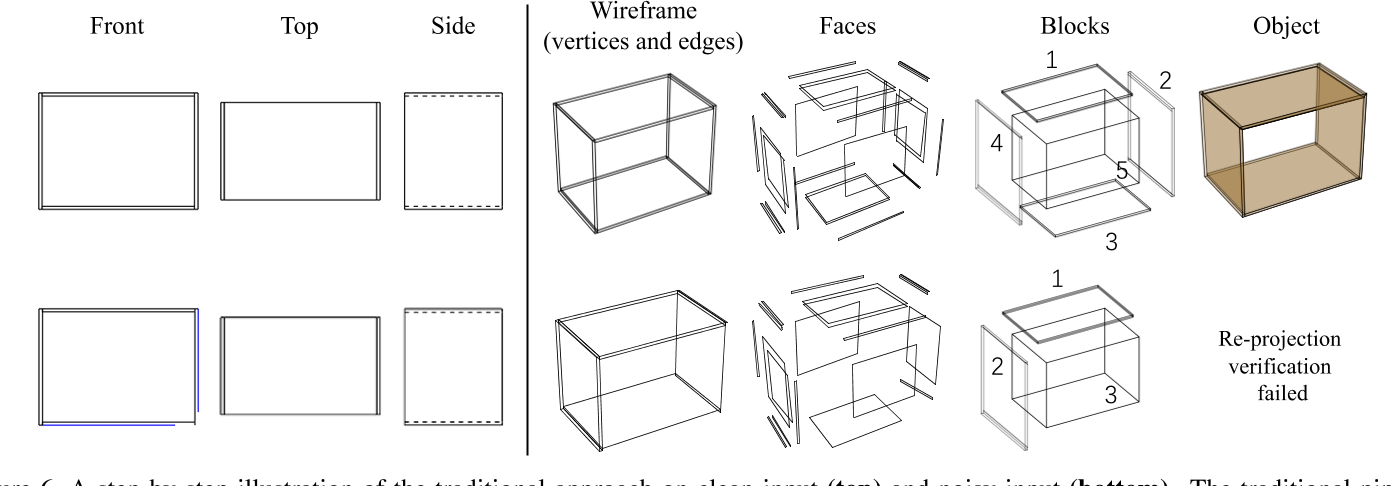
在现有的方法在实践中面临的挑战中，它们对图纸中的错误和缺失部件的敏感性可以说是最关键的。为了理解这个问题，我们注意到几乎所有现有的方法都遵循3D重建的标准程序，其中包括以下步骤:
(i)从2D顶点生成3D顶点;
(ii)从三维顶点生成三维边缘;
(iii)由三维边缘生成三维面;
(iv)从3D面构建3D模型(如图6所示)。遵循管道的一个主要好处是可以找到与输入视图匹配的所有解决方案，因为它在3D模型中的实体和绘图中的实体之间建立了显式的对应关系。但在实践中，设计师并不会花额外的精力去完善图纸，只要能传达他们的想法，他们就会认为一幅图纸足够好。因此，某些实体可能是错误的或缺失的。因此，前面提到的管道经常无法找到所需的解决方案。

image.png

因此，为了克服这一困难，有必要以更全面的方式对二维图形进行推理，并在输入和输出之间实现更灵活的映射。最近，Transformer[29]已经成为许多NLP和CV任务的标准架构。它在序列到序列(seq2seq)问题中特别有效，例如机器翻译，其中关于上下文的推理以及输入和输出之间的软对齐是至关重要的。受此启发，我们将问题转化为seq2seq问题，并提出了一种基于transformer的深度学习方法。直观上，自关注模块可以让模型捕捉到产品设计师的意图，即使他们的图纸不完美，交叉关注模块可以实现2D图纸和3D模型中几何实体之间的灵活映射。

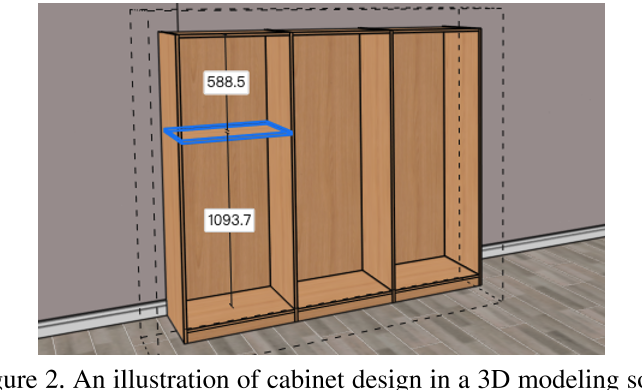
对几何实体使用学习表征和软对齐的另一个好处是，人们可以自由选择如何构建3D模型。这为我们提供了将领域知识合并到我们的方法中以提高其性能的机会。为了说明这一点，本文将重点放在一个特定类型的产品——橱柜家具上。如图2所示，一个橱柜通常是通过在3D建模软件中排列和连接一些木板(即木板)来构建的。为此，我们开发了一种简单的领域特定语言(DSL)，它基于声明木板，然后将它们彼此连接起来，这样每个柜子就可以用一个程序来表示。最后，给定输入的正交视图，我们训练基于transformer的模型来预测与机柜相关的程序。

image.png

为了系统地评估这些方法，我们为此任务构建了一个新的基准数据集，该数据集由26,000多个3D橱柜模型组成。其中大部分是由专业室内设计师使用商业3D建模软件创建的。大量的实验表明，我们的方法对不完美输入具有更强的鲁棒性。例如，当输入图纸中30%的线条损坏或缺失时，传统方法的F1分数为8.20%，而我们的方法的F1分数为90.14%。

总之，这项工作的贡献是:
(i)据我们所知，我们是第一个在三维CAD模型重建任务中使用深度生成模型的人。与现有方法相比，我们的模型学习了更灵活的输入和输出之间的映射，从而对有噪声或不完整的输入具有更强的鲁棒性。
(ii)我们提出了一种新的网络设计，它学习形状程序将木板组装成3D机柜模型。这样的设计不仅提高了重建的精度，而且方便了CAD模型编辑等下游应用。

3D reconstruction from three orthographic views 从三个正射视图中恢复三维模型的研究可以追溯到70年代和80年代[13,22,32,25,10]。关于这一主题的早期调查出现在[31]。根据[31]，为了获得边界表示(Brep)格式的3D对象，现有方法采用四阶段方案，在前几步的结果基础上逐步构建3D顶点、边、面和块。如前所述，该框架的一个关键优势是可以找到与输入视图完全匹配的所有可能的解决方案。
该任务的后续方法[37,38,28,18,21,8,9]也遵循相同的步骤，并侧重于扩展方法的适用范围以覆盖更多类型的对象。

  • 例如，Shin和Shin[28]开发了一种方法来重建由平面和有限二次面组成的物体，如圆柱体和环面，它们平行于一个主轴。
  • Liu等[21]为了消除对曲面轴线的限制，设计了一种将二次曲线的几何性质与仿射性质相结合的算法。
  • 后来，Gong等人[9]提出通过链接关系图(Link-Relation Graph, LRG)中基于提示的模式匹配来识别二次曲面特征，将适用范围扩大到包括具有交互二次曲面的对象。
  • 然而，所有这些方法都假设输入是干净的，并且正如我们将在实验部分所示，在存在误差和噪声的情况下很容易崩溃。

最近，Han等人[12]也训练了一个深度网络来从三个正射视图重建3D模型。然而，他们的方法以栅格图像作为输入，并产生非结构化点云格式的结果，这在CAD建模应用中几乎没有用处。相比之下，我们的方法直接使用矢量化的线条图作为输入，并生成结构化的CAD模型作为输出。

Deep generative models for CAD 随着ABC[17]和Fusion 360 Gallery[34]等大规模CAD数据集的可用性，最近的一系列工作训练深度网络以2D草图[33,7,27]或3D模型[35,14,11,36]的形式生成结构化CAD数据。这些方法都将其视为序列生成问题，但用于产生输出的DSLs有所不同。我们通过将木板模型组装在一起来生成橱柜家具的想法受到ShapeAssembly[15]的启发，ShapeAssembly学习以分层3D零件图的形式生成对象。然而，与上述研究关注生成模型本身不同，我们提出利用生成模型从三个正射影视图构建有效的三维CAD模型重建方法。

A Simple Assembly Language for Cabinets

在本节中，我们的目标是为感兴趣的形状(即橱柜家具)定义特定于领域的语言domain-specific language(DSL)。使用这种语言，每个机柜模型都可以用形状程序表示，然后将其转换为标记序列，作为基于transformer的seq2seq模型的输出。

我们以类似于人类设计师在3D建模软件中构建模型的方式来定义我们的DSL。如图2所示，一个机柜通常是由一列木板模型组装而成的。实际上，大多数木板都是轴线排列的长方体。因此，我们使用长方体作为我们语言中唯一的数据类型。在第6节中，我们将讨论如何扩展我们的方法以适应更复杂的形状(例如，具有非矩形轮廓的木板)。

轴向长方体有6个自由度(DOF)，分别对应三个轴的起始和结束坐标:
$\operatorname{Cuboid}(x_{\min},y_{\min},z_{\min},x_{\max},y_{\max},z_{\max}).$ Eq.1

在实践中，人类设计人员经常使用附件操作attachment operation，而不是为所有坐标指定数值。作为几何约束的一种形式，使用附件的好处至少是双重的:

  • 首先，它使用户能够快速指定木板的位置，而无需显式计算(一些)其坐标;
  • 其次，它促进了未来的编辑，因为对木板所做的任何更改都将自动传播到其他木板。
  • 以图2为例。当添加一个木板(以蓝色突出显示)时，设计师可以将它的四个侧面附加到现有的木板上(包括不可见的边界框)，同时以数值指定到顶部和底部的距离。

image.png

我们的语言采用编程语言(如c++)中常用的union结构，支持通过数值或附加操作来指定木板坐标。如右图所示，式(1)中的六个坐标可以是数值，也可以是指向另一个长方体(它所依附的长方体)对应坐标的指针。图3显示了一个通过强制执行程序命令(程序1)逐步构建的示例机柜。

1
union Coord{ float v; float* p; };

image.png

程序1：

1
2
3
4
5
6
7
8
bbox = Cuboid(-0.35, -0.23, -0.76, 0.35, 0.23, 0.76)
plank1 = Cuboid(bbox1 , bbox2 , bbox3 , -0.34, bbox5, bbox6 )
plank2 = Cuboid(0.34, bbox2 , bbox3 , bbox4 , bbox5 , bbox6 )
plank3 = Cuboid(plank14 , bbox2 , -0.70, plank21 , bbox5 , -0.69)
plank4 = Cuboid(plank14 , bbox2 , 0.75, plank21 , bbox5 , bbox6 )
plank5 = Cuboid(plank14 , 0.21, plank36 , plank21 , 0.22, plank43 )
plank6 = Cuboid(plank14 , bbox2 , bbox3 , plank21, -0.21, plank33 )
plank7 = Cuboid(plank14 , 0.21, bbox3 , plank21 , bbox5 , plank33 )

Shape program as a DAG

或者，我们可以将形状程序解释为有向无环图(DAG)。请注意，每个平板模型由六个面组成，其中每个面正好对应于轴向长方体中的一个自由度$(i.e.,{x_\mathrm{min}},y_\mathrm{min},z_\mathrm{min},x_\mathrm{max},y_\mathrm{max},z_\mathrm{max}).$。因此，每个程序都可以用图$\mathcal{G}=\{\mathcal{F},\mathcal{E}\},$来表征，其顶点$\mathcal{F}=\{f_1,\ldots,f_{|\mathcal{F}|}\}$表示木板模型的面，其边$\mathcal{E}=\{e_{1},\ldots,e_{|\mathcal{E}|}\}$表示面之间的依恋关系。每个有向边$e_{i{\to}j}$都是一对有序的顶点$(f_i,f_j)$，表示第i个面$f_{i}$连接到第j个面$f_{j}$。我们假设每个面最多可以与另一个面相连;也就是说，任何面$f_{i}$的输出度最多为1。进一步，这些边可以用邻接矩阵$A\in\mathbb{R}^{|\mathcal{F}|\times|\mathcal{F}|}$来表示。具体来说，如果$f_{i}$指向$f_{j}$, $A_{ij}$为1，否则为0。

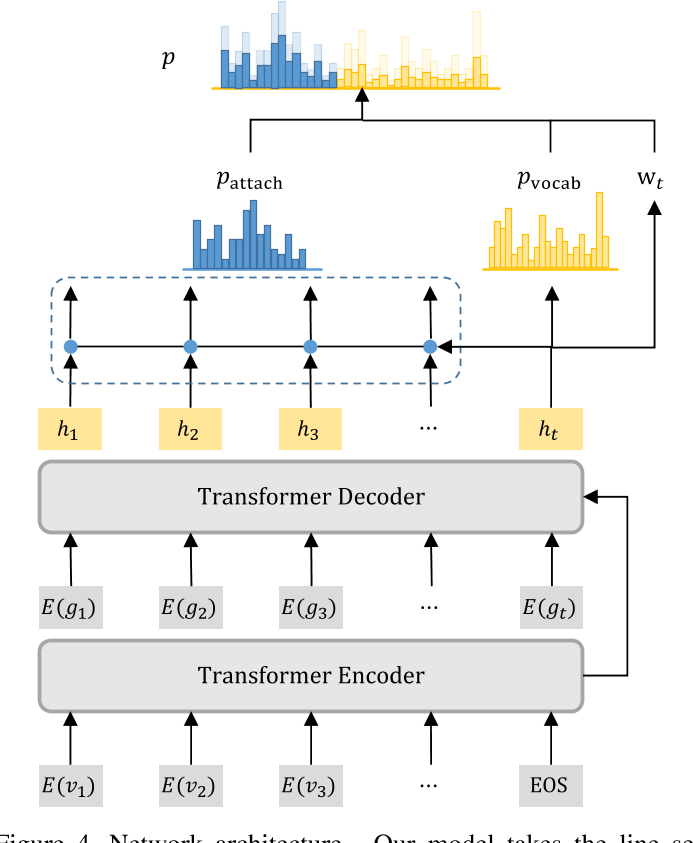
The PlankAssembly Model

如图1所示，我们假设输入由物体的三个正射影组成，即前视图、俯视图和侧视图:$\mathcal{V}=\{V_{F},V_{T},V_{S}\}$。每个视图都可以看作是一个二维边和边相交节点的平面图。我们用实线表示可见的边缘，虚线表示隐藏的边缘。我们的目标是重建由形状程序或等效DAG $\mathcal{G}$描述的三维机柜模型。

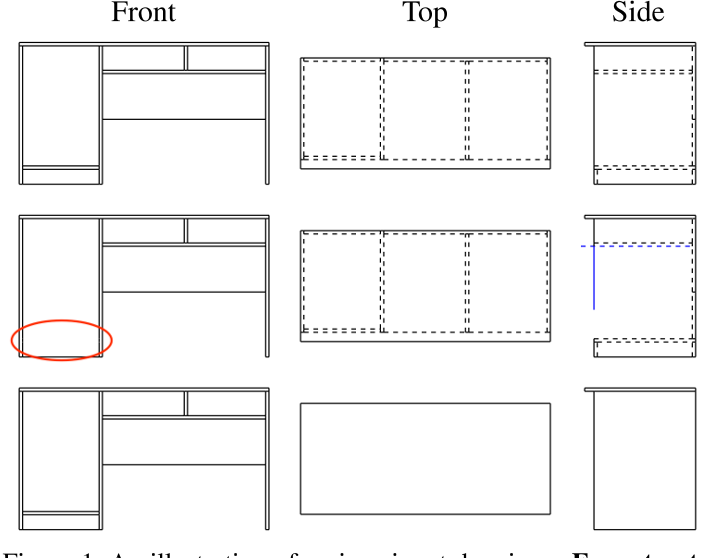
image.png

在本文中，我们把三维重建视为一个seq2seq问题。在4.1节和4.2节中，我们描述了如何将输入视图$\mathcal{V}$和形状程序$\mathcal{G}$分别编码为1D序列$\mathcal{V}^{seq}$和$\mathcal{G}^{seq}$。然后，我们在4.3节中介绍了我们的浮游装配模型的设计，该模型采用基于变压器的编码器-解码器架构来学习概率分布$p(\mathcal{G}^\mathrm{seq}\mid\mathcal{V}^\mathrm{seq}),$。最后，我们将在4.4节中介绍实现细节。

Input Sequences and Embeddings

对于输入条件，我们首先按视图$\mathcal{V}$对2D边进行排序。每条二维边都写成$(x_{1},y_{1},x_{2},y_{2})$，其中我们按照x坐标从低到高排序它的两个端点，然后是y坐标(如果$x_1 = x_2$)。然后，我们用$x_1, x_2, y_1, y_2$来排序一组二维边。接下来，我们将所有边平铺成1D序列$\mathcal{V}^{\mathrm{seq}}=\{v_{1},\ldots,v_{N_{v}}\}.$。注意，由于每条2D边都有四个自由度(即两个端点的x坐标和y坐标)，所以$\mathcal{V}_{\mathrm{seq}}$的长度为$N_{v}=4N_{\mathrm{edge}}$，其中$N_{\mathrm{edge}}$是所有三个正射影视图中2D边的总数。
我们将第 i 个标记 $v_{i}$ 嵌入为

$\begin{aligned}E(v_i)=E_{\mathrm{value}}(v_i)+E_{\mathrm{view}}(v_i)+E_{\mathrm{cdge}}(v_i)\+E_{\mathrm{coord}}(v_i)+E_{\mathrm{type}}(v_i),\end{aligned}$ Eq.2

  • 值嵌入$E_{\mathrm{value}}$表示token令牌的量化坐标值，
  • 视图嵌入$E_{\mathrm{view}}$表示2D边缘来自哪个视图(即前视图、前视图或侧视图)，
  • 边缘嵌入$E_{\mathrm{edge}}$表示2D边缘在对应视图中的相对位置，
  • 坐标嵌入$E_{\mathrm{coord}}$表示坐标在对应2D边缘的相对位置。
  • 最后，我们使用类型嵌入 Etype 来表示 2D 边缘是否可见或隐藏。

在本文中，我们将坐标值量化为 9 位整数，并为方程式中的每一项使用学习的 512-D 嵌入。 (2)。

Output Sequences and Embeddings

为了按顺序生成形状程序，我们需要将图 G 映射到序列 $\mathcal{G}^{\mathrm{seq}}$。这需要我们在 G 上定义一个顶点顺序 π：

  • 我们首先在拓扑上对顶点进行排序，确保直接后继者在其相应的直接前辈之前列出。
  • 然后，不直接连接的顶点按坐标值排序。

这给了我们一个排序图$\mathcal{G}^{\pi}$，其顶点 $\mathcal{F}^{\pi}$遵循顺序 π。

由于我们想捕获建模过程并促进未来的编辑，我们将附件关系优先于几何实体。与输入序列编码类似，我们展平 $\mathcal{G}^{\pi}$ 以获得一维序列 $\mathcal{G}^{seq}$。序列 $\mathcal{G}^{seq}$ 的第 i 个元素可以得到：

$g_i=\begin{cases}f_i^\pi,&\text{if}A_{ij}^\pi=0,\forall j,\\e_{i\to j}^\pi,&\text{if}A_{ij}^\pi=1.\end{cases}$ Eq.3

此外，我们使用两个特殊标记 [SOS] 和 [EOS] 分别表示输出序列的开始和结束

对于我们模型的解码器的输入，我们使用相关的面 $f_{i}^{\pi}$ 嵌入令牌 $g_{i}$，如下所示：
$E(g_i)=E(f_i^\pi)=E_{\text{value}}(f_i^\pi)+E_{\text{plank}}(f_i^\pi)+E_{\text{face}}(f_i^\pi).$ Eq.4

  • 值嵌入 $E_{\mathrm{value}}$ 表示量化的坐标值，该值用于输入和输出序列。
  • plank 嵌入 $E_{\mathrm{plank}}$表示柜模型中相应plank的位置，
  • 面嵌入$E_{\mathrm{face}}$ 表示面在plank内的相对位置。

如果令牌对应于 G 中的一条边 $e_{i\to j}^{\pi}$，我们将识别当前面$f_{i}^{\pi}$附加的人脸 $f_{j}^{\pi}$，并使用与$f_{j}^{\pi}$相同的值嵌入。

Model Design

为了解决这个 seq2seq 问题，我们将输出序列上的联合分布分解为一系列条件分布：
$p(\mathcal{G}^{\mathrm{seq}}\mid\mathcal{V}^{\mathrm{seq}})=\prod_{t}p\left(g_{t}\mid\mathcal{G}_{<t}^{\mathrm{seq}},\mathcal{V}^{\mathrm{seq}}\right).$ Eq.5

在这里，由于 $g_t$ 可以采用几何实体（即$f_{i}^{\pi}$ ）或附件关系（即 $e_{i\to j}^{\pi}$）的形式，我们需要在固定长度的词汇表集（量化坐标值）加上输出序列中的可变长度标记集 $\mathcal{G}_{<t}^{\mathrm{seq}}$上产生概率分布。

前者分布是一个分类分布，通常用于分类任务。设$\mathbf{h}_t$是解码器在时间 t 获得的隐藏特征，我们通过线性层将其投影到词汇表的大小，然后将其归一化以形成有效分布：

$p_{\mathrm{vocab}}(g_{t}\mid\mathcal{G}_{<t}^{\mathrm{seq}},\mathcal{V}^{\mathrm{seq}})=\mathrm{softmax}\left(\mathrm{linear}\left(\mathbf{h}_{t}\right)\right).$ Eq.6

为了生成输出序列 $\mathcal{G}_{<t}^{\mathrm{seq}}$ 在时间t 上的分布，我们采用指针网络 [30]。具体来说，我们首先使用线性层来预测指针。然后，通过点积将指针与所有前一步的隐藏特征进行比较。最后，输出序列上的分布是通过 softmax 层获得的：

$p_\mathrm{attach}(g_t\to g_k\mid\mathcal{G}_{<t}^\mathrm{seq},\mathcal{V}^\mathrm{seq})=\mathrm{softmax}_k\left(\mathrm{linear}\left(\mathbf{h}_t\right)^T\mathbf{h}_{<t}\right).$ Eq.7

我们没有直接比较这两个分布，而是遵循 Pointer-Generator Networks [26] 并引入附件概率 $w_{t}$ 来加权这两个分布。附件概率 $w_{t}$ 是通过线性层和 sigmoid 函数 σ(·) 获得的：$\sigma(\cdot) : w_{t}=\sigma(linear(\mathbf{h}_t))$。因此，最终分布是两个加权分布的串联concatenation：
$p(g_t\mid\mathcal{G}_{<t}^{\text{seq}},\mathcal{V}^{\text{seq}})=\text{concat}\left\{(1-w_t)\cdot p_{\text{vocab}},w_t\cdot p_{\text{attach}}\right\}.$ Eq.8

最后，给定一个训练集，可以通过标准的交叉熵损失最大化条件分布Eq.(8)来学习模型的参数。

Network architecture

我们使用标准 Transformer 块 [29] 作为我们 PlankAssembly 模型的基本块。给定输入嵌入 $\{E(v_1),E(v_2),\ldots\},$编码器将它们编码为上下文嵌入。在解码时间 t，解码器根据上下文嵌入和解码器输入 $\{E(g_{1}),E(g_{2}),\ldots\}.$生成隐藏特征 $\mathbf{h}_{t}$。我们为编码器和解码器使用 6 个 Transformer 层。每层的前馈维度为 1024 和 8 个注意力头。网络架构如图 4 所示。

image.png

Implementation Details

Training。我们使用 PyTorch Lightning [1] 实现我们的模型。我们为编码器和解码器使用 6 个 Transformer 层。每层的前馈维度为 1024 和 8 个注意力头。该网络在四个NVIDIA RTX 3090 GPU设备上训练了400K次迭代。我们使用学习率为 10−4 的 Adam 优化器 [16]。每个 GPU 的批量大小设置为 16。

Inference。在推理时，我们采取几个步骤来确保我们模型中的有效预测。首先，我们观察到两个附加面必须对应于同一轴上的相反自由度，以避免任何空间冲突。例如，一个 plank 的 $x_min$ 标记只能指向另一个 plank 的 $x_max$ 标记，反之亦然。因此，我们在推理过程中屏蔽所有无效位置。其次，我们过滤掉体积为零的预测计划。

Experiments

Experimental Setup

数据集。我们为此任务创建了一个大规模的基准数据集，利用来自Kujiale1的大型橱柜家具模型存储库，这是一个内部设计行业的在线 3D 建模平台。存储库中的大多数模型都是由专业设计师使用商业参数建模软件创建的，并用于现实世界的生产。
几个规则用于过滤数据：
(i) 我们根据三个正字法orthographic视图的相似性删除重复的 3D 模型；
(ii) 我们排除了少于四个 planks 的模型，超过 20 个 planks，或总共超过 300 个边缘。
其余数据被随机分成三部分：24039 个用于训练，1329 个用于验证，1339 个用于测试。
为了合成三个正字法视图，我们使用来自pythonOCC[3]的HLRBRep Algo API，该API建立在Open CASCADE技术建模内核[2]之上。

对于我们的任务，我们需要将每个参数柜模型解析为形状程序。我们首先提取橱柜模型中的几何实体来获得planks。请注意，在参数建模软件中，通常通过首先绘制 2D 轮廓然后应用挤压命令来创建 plank。因此，我们将每个 plank 的面分为侧面或端面，这取决于它们是否沿挤压方向。然后，给定来自两个不同planks的一对face，我们认为如果 (i) 两个face在 1mm 的距离阈值内，则存在附件关系，并且 (ii) 该对由一个侧面和一个结束面组成。最后，在G中添加了从端面到侧面的有向边

Evaluation metrics 为了评估 3D 重建结果的质量，我们使用了三个标准指标：精度precision、召回率recall和 F1 分数F1 score。
具体来说，对于橱柜模型，我们使用匈牙利匹配来匹配预测的planks和ground truth planks。如果具有一个gt的 3D intersection-over-union (IOU) 大于 0.5，则该预测被认为是真阳性。

Comparison to Traditional Methods

在本节中，我们系统地将我们的方法与从三个正字法视图进行 3D 重建的传统方法进行了比较。由于没有公开实现传统管道，我们通过紧跟之前的工作 [25, 28] 重新实现管道。回想一下，从输入视图开始，传统的管道逐步生成 3D 顶点、3D 边、3D 面和 3D 块。然后，通过枚举候选块的所有组合并检查它们的 2D 投影是否与输入视图匹配来找到解决方案。

Welcome to my other publishing channels