| Title | Recovering Fine Details for Neural Implicit Surface Reconstruction |
|---|---|
| Author | Decai Chen1, Peng Zhang1,2, Ingo Feldmann1, Oliver Schreer1, and Peter Eisert1,3 |
| Conf/Jour | WACV |
| Year | 2023 |
| Project | fraunhoferhhi/D-NeuS: Recovering Fine Details for Neural Implicit Surface Reconstruction (WACV2023) (github.com) |
| Paper | Recovering Fine Details for Neural Implicit Surface Reconstruction (readpaper.com) |
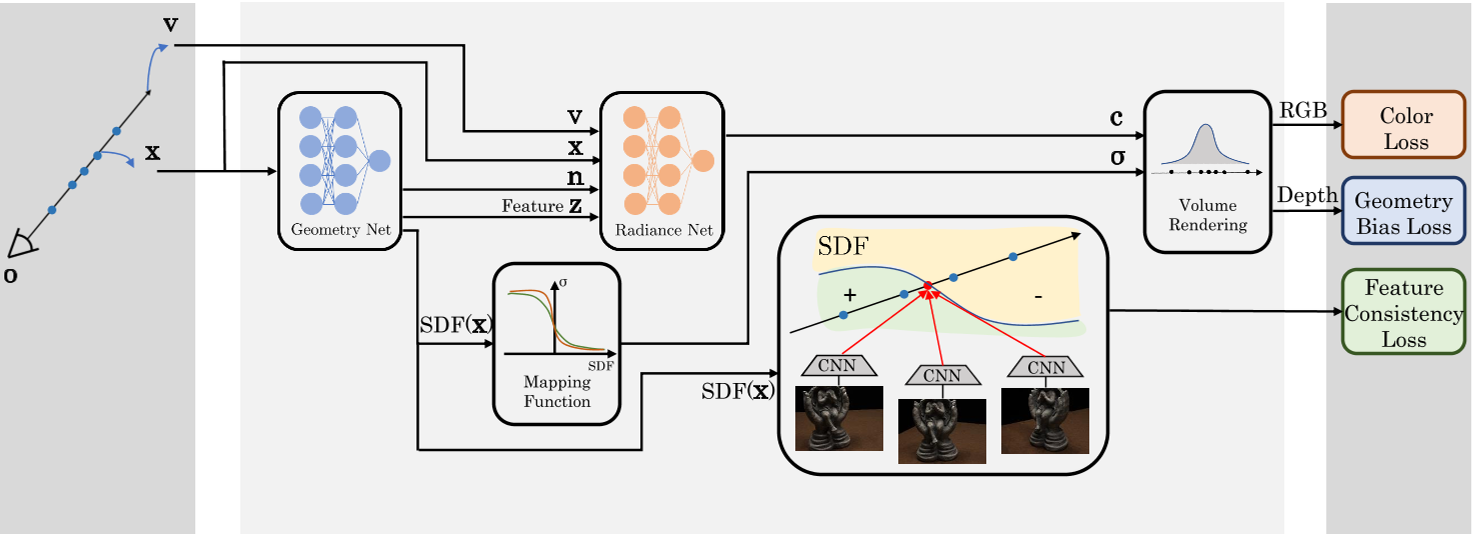
Idea:两个额外的损失函数
- 几何偏差损失:鼓励隐式SDF场和体渲染的亮度场之间的几何一致性
- 多视图特征一致性损失:多个观察视图在表面点处的特征一致
Abstract
最近关于内隐神经表征的研究取得了重大进展。利用体绘制学习隐式神经表面在无三维监督的多视图重建中得到了广泛的应用。然而,由于几何和外观表现的潜在模糊性,准确地恢复精细细节仍然具有挑战性。在本文中,我们提出了D-NeuS,一种基于体绘制的神经隐式表面重建方法,能够恢复精细的几何细节,它通过两个额外的损失函数来扩展NeuS,目标是提高重建质量。首先,我们鼓励从alpha合成中渲染的表面点具有零符号距离值,减轻了将SDF转换为体渲染密度所产生的几何偏差。其次,我们通过沿射线插值采样点的SDF归零来对表面点施加多视图特征一致性。大量的定量和定性结果表明,我们的方法重建高精度的表面与细节,并优于目前的状态。
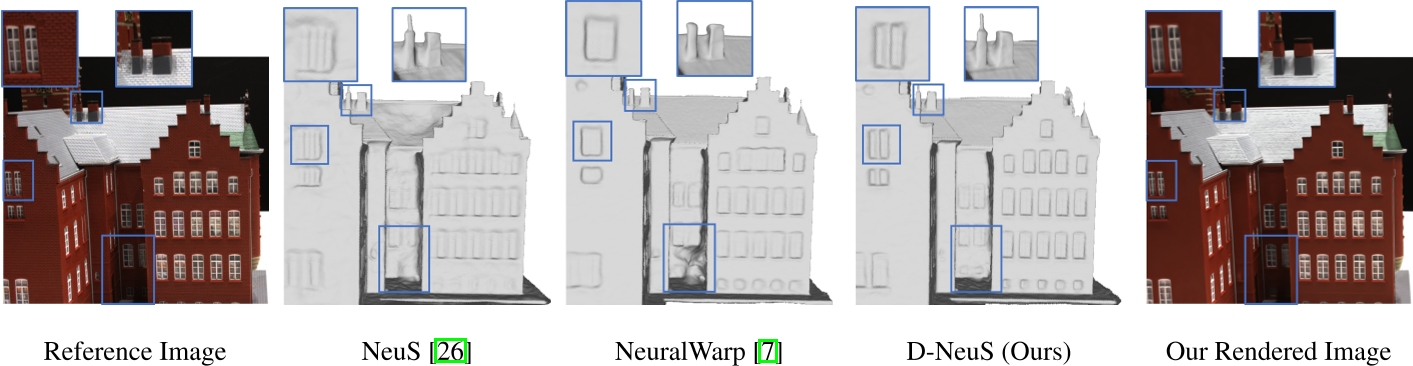
neus局限
neus的unregularized sdf导致体渲染积分和SDF隐式表面之间存在偏差,颜色亮度场和几何SDF场之间的不一致导致了不理想的表面重建
单一平面相交的简单情况下,密度和权函数在不同SDF分布下的表现,显示出了非线性SDF值导致几何表面(橙色虚线)和体积渲染表面点(蓝色虚线)之间的偏差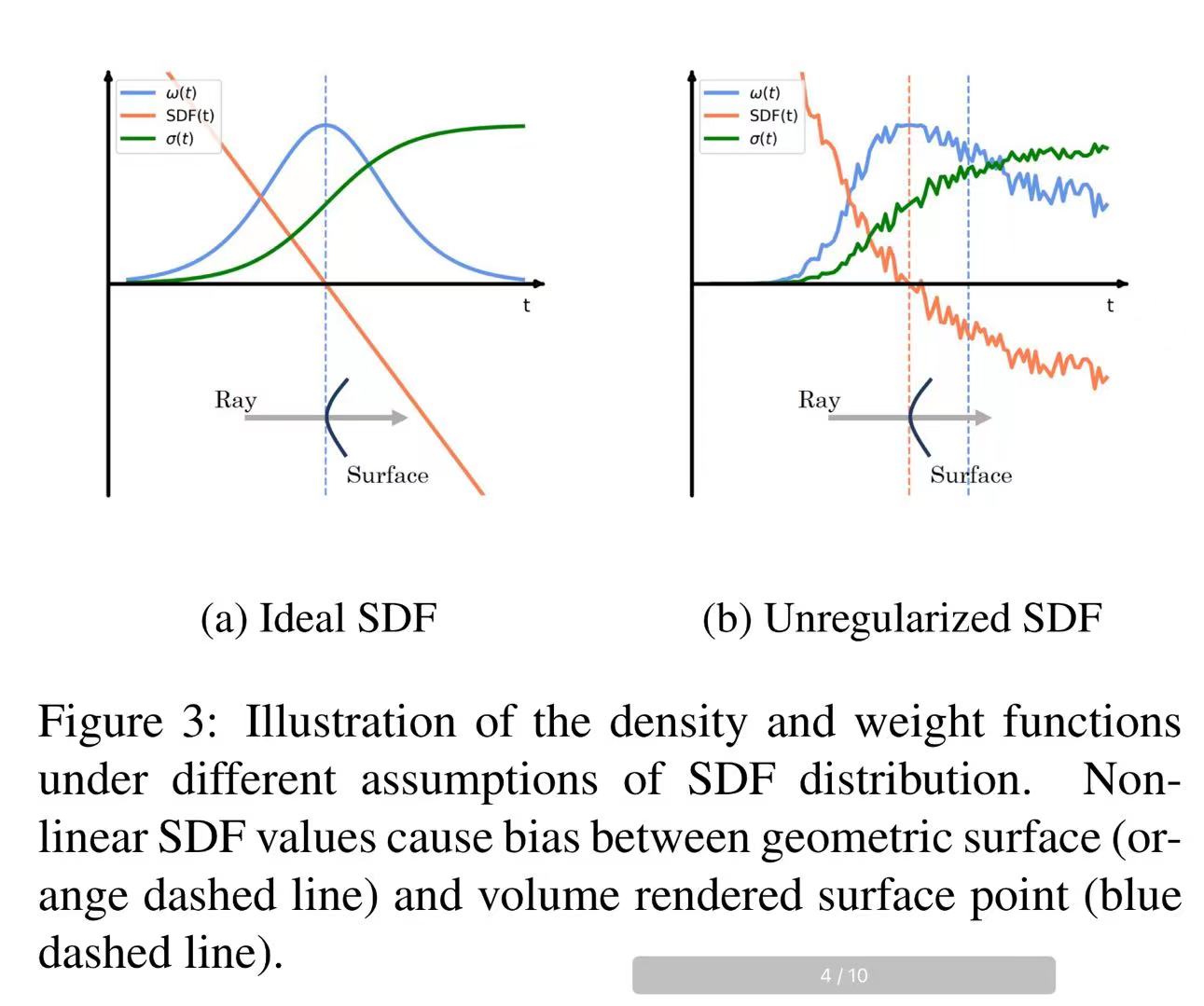
Method
添加了两个损失项:
几何偏差损失:鼓励隐式SDF场和体渲染的亮度场之间的几何一致性
$\mathcal{L}_{bias}=\frac1{|\mathbb{S}|}\sum_{\mathbf{x}_{rendered}\in\mathbb{S}}|f(\mathbf{x}_{rendered})|,$
- $t_{rendered}=\sum_{i}^{n}\frac{\omega_{i}t_{i}}{\sum_{i}^{n}\omega_{i}},$
- $\mathbf{x}_{rendered}=\mathbf{o}+t_{rendered}\mathbf{v}.$
- S为光线与表面的交点的集合
- 几何偏差损失与Eikonal损失相互支持,提高了重建质量
Multi-view Feature Consistency多视图特征一致性损失
首先找到光线与表面的交点:
- s点sdf值大于0,s的下个采样点sdf值小于0:$s=\arg\min_i\{t_i\mid f(\mathbf{x}(t_i))>0andf(\mathbf{x}(t_{i+1}))<0\}$
- 根据s点和s的下个采样点s+1,使用可微线性插值可以得到表面点:$\hat{\mathbf{x}}=\left\{\mathbf{x}(\hat{t})\mid\hat{t}=\frac{f(\mathbf{x}(t_s))t_{s+1}-f(\mathbf{x}(t_{s+1}))t_s}{f(\mathbf{x}(t_s))-f(\mathbf{x}(t_{s+1}))}\right\}.$
$\mathcal{L}_{feat.}=\frac{1}{N_{c}N_{v}}\sum_{i=1}^{N_{v}}|\mathbf{F}_{0}(\mathbf{p}_{0})-\mathbf{F}_{i}(\mathbf{K}_{i}(\mathbf{R}_{i}\hat{\mathbf{x}}+\mathbf{t}_{i}))|,$
- Nv和Nc分别为相邻源视图和特征通道的个数
- F为提取的特征映射
- p0为光线投射的像素
- {Ki, Ri, ti}为第i个源视图的相机参数
总损失:$\mathcal{L}=\mathcal{L}_{color}+\alpha\mathcal{L}_{eik.}+\beta\mathcal{L}_{bias}+\gamma\mathcal{L}_{feat.}.$
Experiments
数据集:BlendedMVS + DTU
Baseline:COLMAP, IDR [33], MVSDF [37], VolSDF [32], NeuS [26], NeuralWarp [7].