QiYun

Note

Instant-NSR代码理解

Posted on Edited on In
2.3k 8 mins.

对Instant-NSR代码的理解

训练流程图

神经网络结构

Neus网络

in network_sdf.py NeRFNetwork(NeRFRenderer)

Instant-NSR训练隐式模型的网络由两个串联的MLP组成：

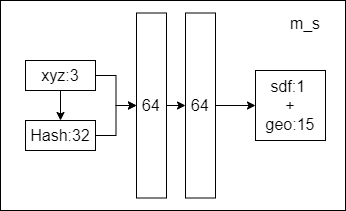
  • 一个具有2个隐藏层的SDF MLP $𝑚_{𝑠}$
    • 每个隐藏层宽度为64个神经元
    • 用Softplus替换了原始的ReLU激活函数，并且对所有隐藏层的激活函数设置了𝛽=100，SDF MLP使用哈希编码函数(NGP)将3D位置映射为32个输出值。
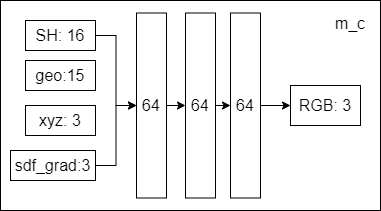
  • 一个具有3个隐藏层的颜色MLP $𝑚_{𝑐}$
    • 每个隐藏层宽度为64个神经元

$m_{s}$训练SDF的网络表示为:$(x,F_{geo})=m_{s}(p,F_{hash}).$

  • input
    • 每个三维采样点的3个输入空间位置值
    • 来自哈希编码位置的32个输出值
  • output
    • sdf值，然后我们将截断的函数应用于输出SDF值，该值使用sigmoid激活将其映射到[−1,1]：sigma = F.relu(h[..., 0])
    • 15维的$F_{geo}$值

m_s.png

$m_{c}$训练颜色的网络表示为：$\hat{C}=m_{c}(\mathrm{p},\mathrm{n},\mathrm{v},F_{geo}).$

  • input
    • 视角方向在球谐函数基础上分解为4阶及以下的前16个系数
    • SDF MLP的15维的输出值$F_{geo}$
    • 每个三维采样点的3个输入空间位置值
    • 用有限差分函数估计SDF梯度的3个正态值
  • output
    • RGB: 3

用sigmoid激活将输出的RGB颜色值映射到[0,1]范围

m_c.png

训练细节

我们在论文中证明了我们约10分钟的训练结果与原始NeuS的约8小时优化结果是可比较的。在优化阶段，我们假设感兴趣的区域最初位于单位球内。

  • 分层采样：我们在PyTorch实现中采用了NeRF的分层采样策略，其中粗采样和细采样的数量分别为64和64。我们每批次采样4,096条光线，并使用单个NVIDIA RTX 3090 GPU进行为期6,000次迭代的模型训练，训练时间为12分钟。
  • 法线计算：为了近似梯度以进行高效的法线计算，我们采用有限差分函数$𝑓 ′ (𝑥) = (𝑓 (𝑥 + Δ𝑥) − (𝑓 𝑥 − Δ𝑥))/2Δ𝑥$。在我们的PyTorch实现中，我们将近似步长设置为Δ𝑥 = 0.005，并在训练结束时将其减小到Δ𝑥 = 0.0005。
  • Loss：我们通过最小化Huber损失$L_{𝑐𝑜𝑙𝑜r}$和Eikonal损失$L_{𝑒𝑖𝑘}$来优化我们的模型。这两个损失使用经验系数𝜆进行平衡，在我们的实验中将其设置为0.1。
  • Adam：我们选择Adam优化器，初始学习率为$10^{−2}$，并在训练过程中将其降低到$1.6 \times 10^{-3}$。

有限差分法：

有限差分法 - 维基百科，自由的百科全书 (wikipedia.org)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def gradient(self, x, bound, epsilon=0.0005):
    #not allowed auto gradient, using fd instead
    return self.finite_difference_normals_approximator(x, bound, epsilon)

def finite_difference_normals_approximator(self, x, bound, epsilon = 0.0005): # 有限差分法
    # finite difference
    # f(x+h, y, z), f(x, y+h, z), f(x, y, z+h) - f(x-h, y, z), f(x, y-h, z), f(x, y, z-h)
    pos_x = x + torch.tensor([[epsilon, 0.00, 0.00]], device=x.device)
    dist_dx_pos = self.forward_sdf(pos_x.clamp(-bound, bound), bound)[:,:1]
    pos_y = x + torch.tensor([[0.00, epsilon, 0.00]], device=x.device)
    dist_dy_pos = self.forward_sdf(pos_y.clamp(-bound, bound), bound)[:,:1]
    pos_z = x + torch.tensor([[0.00, 0.00, epsilon]], device=x.device)
    dist_dz_pos = self.forward_sdf(pos_z.clamp(-bound, bound), bound)[:,:1]

    neg_x = x + torch.tensor([[-epsilon, 0.00, 0.00]], device=x.device)
    dist_dx_neg = self.forward_sdf(neg_x.clamp(-bound, bound), bound)[:,:1]
    neg_y = x + torch.tensor([[0.00, -epsilon, 0.00]], device=x.device)
    dist_dy_neg  = self.forward_sdf(neg_y.clamp(-bound, bound), bound)[:,:1]
    neg_z = x + torch.tensor([[0.00, 0.00, -epsilon]], device=x.device)
    dist_dz_neg  = self.forward_sdf(neg_z.clamp(-bound, bound), bound)[:,:1]

    return torch.cat([0.5*(dist_dx_pos - dist_dx_neg) / epsilon, 0.5*(dist_dy_pos - dist_dy_neg) / epsilon, 0.5*(dist_dz_pos - dist_dz_neg) / epsilon], dim=-1)

Neural Tracking Implementation Details

在第4节中，我们提出了一种神经跟踪流程，它将传统的非刚性跟踪和神经变形网络以一种由粗到精的方式结合在一起。我们通过高斯-牛顿方法解决非刚性跟踪问题，并在接下来的内容中介绍了详细信息。
跟踪细节: 在进行非刚性跟踪之前，我们通过计算规范网格上的测地距离来对ED节点进行采样。我们计算平均边长，并将其乘以一个半径比例，用于控制压缩程度，以获得影响半径𝑟。通过所有的实验，我们发现简单地调整为0.075也可以得到很好的结果。给定𝑟，我们按Y轴对顶点进行排序，并在距离𝑟之外时从现有ED节点集合中选择ED节点。此外，当ED节点影响相同的顶点时，我们可以将它们连接起来，然后提前构建ED图以进行后续优化。

$\mathrm{(c,\sigma)=\phi^{o}(p’+\phi^{d}(p’,t),d).}$
网络结构: 我们改进阶段的关键包括规范辐射场$𝜙^𝑜$和变形网络$𝜙^𝑑$。

  • $𝜙^𝑜$具有与Instant-NGP相同的网络结构，包括三维哈希编码和两个串联的MLP: 密度和颜色。

    • 三维坐标通过哈希编码映射为64维特征，作为密度MLP的输入。然后，密度MLP具有2个隐藏层（每个隐藏层有64个隐藏维度），并输出1维密度和15维几何特征。
    • 几何特征与方向编码连接在一起，并输入到具有3个隐藏层的颜色MLP中。最后，我们可以获得每个坐标点的密度值和RGB值。

  • $𝜙^{𝑑}$包括四维哈希编码和单个MLP。

    • 四维哈希编码具有32个哈希表，将输入（p′，𝑡）映射到64维特征。通过我们的2个隐藏层变形MLP（每个隐藏层具有128个隐藏维度），最终可以得到Δp′。

训练细节

训练细节。我们分别训练$𝜙^𝑜$和 $𝜙^{𝑑}$ 。我们首先利用多视图图像来训练规范表示 $𝜙^𝑜$。当 PSNR 值稳定下来（通常在100个epoch之后），我们冻结 $𝜙^𝑜$ 的参数。然后，我们训练变形网络 $𝜙^{𝑑}$ 来预测每帧的变形位移。我们构建了一个PyTorch CUDA扩展库来实现快速训练。我们首先将规范帧中的ED节点转换到当前帧，然后构建一个KNN体素。具体而言，我们的体素分辨率是2563到5123，并且对于KNN体素中的每个体素，我们通过堆查询4到12个最近邻的ED节点。基于KNN体素，我们可以快速查询体素中的任何3D点，并获取邻居和对应的蒙皮权重，以通过非刚性跟踪计算坐标。

Neural Blending Implementation Details

U-Net: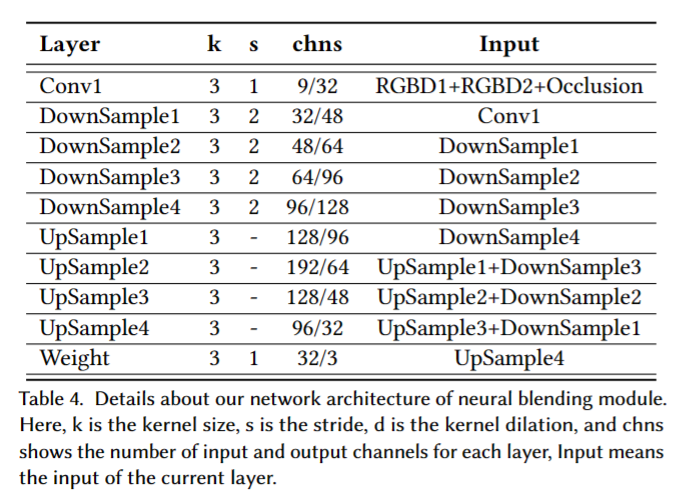
image.png

训练细节

在训练过程中，我们引入了一个称为遮挡映射的新维度，它是两个变形深度图之间的差异计算得出的。然后，我们将遮挡映射（1维）和两个变形的RGBD通道（4维）作为网络输入，进一步帮助U-net网络优化混合权重。在传统的逐像素神经纹理混合过程中，混合结果仅从两个变形图像生成。然而，如果目标视图在相邻虚拟视图中都被遮挡，将导致严重的伪影问题。因此，我们使用纹理渲染结果作为额外输入，以恢复由于遮挡而丢失的部分。为了有效地渲染，我们首先将输入图像降采样为512×512作为网络输入，然后通过双线性插值上采样权重映射以生成最终的2K图像。为了避免混合网络过度拟合额外的纹理渲染输入，我们在训练过程中应用高斯模糊操作来模拟低分辨率的纹理渲染图像。这个操作有助于网络专注于选定的相邻视图的细节，同时从额外的纹理渲染输入中恢复缺失的部分。此外，我们选择Adam [Diederik P Kingma et al.2014]优化器，初始学习率为1e-4，权重衰减率为5e-5。我们在一台单独的NVIDIA RTX 3090 GPU上使用Twindom [web.twindom.com]数据集对神经纹理混合模型进行了两天的预训练。

编码方式

Instant-NSR自己集成了cuda.C++程序，可以实现哈希编码而不需要安装tiny-cuda-nn扩展

encoding.py

hashencoder

psencoder

shencoder

Welcome to my other publishing channels