QiYun

Note

NeuS2

Posted on Edited on In
6.9k 25 mins.
Title NeuS2: Fast Learning of Neural Implicit Surfaces for Multi-view Reconstruction
Author Yiming Wang 1 Qin Han 1 Marc Habermann 2 Kostas Daniilidis 3 Christian Theobalt2 Lingjie Liu 2,3
Conf/Jour ICCV
Year 2023
Project NeuS2: Fast Learning of Neural Implicit Surfaces for Multi-view Reconstruction (mpg.de)
Paper NeuS2: Fast Learning of Neural Implicit Surfaces for Multi-view Reconstruction (readpaper.com)

image.png

在Neus基础上添加了：

  • 哈希编码加速
    • 定制的二阶导数反向传播计算
    • 渐进式学习策略(渐进添加高leve的哈希表)
  • 动态场景重建
    • 全局变换预测
    • 增量训练策略

主要代码通过cuda c++编写

Conclusion

局限:
虽然我们的方法以高质量重建动态场景的每一帧，但帧之间没有密集的表面对应。一种可能的方法是使网格模板变形，以适应我们为每一帧学习的神经表面，就像[9，71]中使用的网格跟踪一样。目前，我们还需要保存每帧（25M）的网络参数。作为未来的工作，可以探索对动态场景进行编码的此类参数的压缩

结论：
我们提出了一种基于学习的方法，以前所未有的运行时性能对静态和动态场景进行精确的多视图重建。为了实现这一点，我们将多分辨率哈希编码集成到神经SDF中，并根据我们的专用网络架构引入了二阶导数的简单计算。为了增强训练收敛性，我们提出了一种渐进式训练策略来学习多分辨率哈希编码。对于动态场景重建，我们提出了一种带有全局变换预测组件的增量训练策略，该策略利用了两个连续帧中的共享几何体和外观信息。

AIR

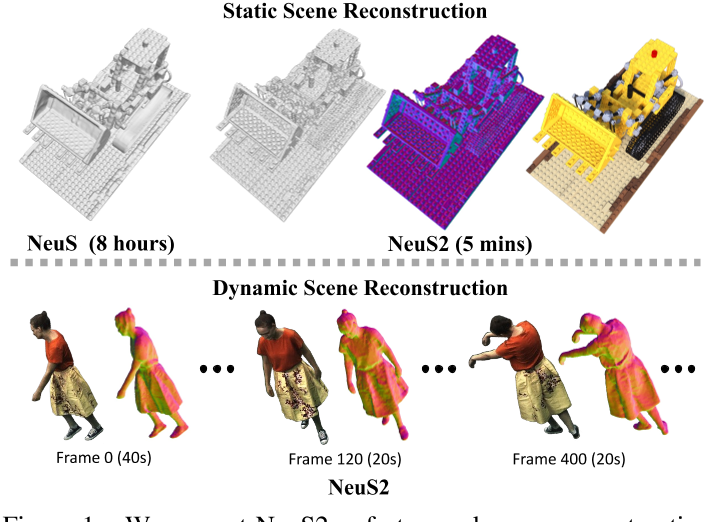
最近的神经表面表示和渲染方法，例如Neus[62]，已经证明了静态场景的高质量重建。然而，Neus的训练时间非常长(8小时)，这使得它几乎不可能应用到数千帧的动态场景中。我们提出了一种快速的神经表面重建方法，称为NeuS2，在不影响重建质量的情况下，在加速方面实现了两个数量级的改进。为了加速训练过程，我们通过多分辨率哈希编码参数化神经表面表示，并提出了一种针对我们的网络定制的二阶导数的新型轻量级计算，以利用CUDA并行性，实现了两倍的速度提升。为了进一步稳定和加速训练，提出了一种渐进式学习策略，将多分辨率哈希编码从粗到细进行优化。
我们扩展了动态场景的快速训练方法，提出了一种增量训练策略和一种新的全局变换预测组件，使我们的方法能够处理具有大运动和变形的具有挑战性的长序列。
我们在各种数据集上的实验表明，无论是静态场景还是动态场景，NeuS2在表面重建精度和训练速度方面都明显优于目前的技术水平。

Introduction

  • Reconstructing the dynamic 3D world from 2D images的应用：AR/VR、3D电影、游戏、telepresence、3D打印等等
    • 传统方法：如特征匹配，仍然相对缓慢，难以重建高质量的结果。
    • 基于隐式表示的三维重建：如Neus可以产生高质量的重建结果，但其训练过程非常缓慢
    • Instant-NGP通过利用多分辨率哈希表增强神经网络编码的辐射场，探索了神经辐射场(NeRF)的训练加速，但由于三维表示缺乏表面约束，从学习的密度场中提取的几何形状包含可识别的噪声

为了克服这些缺点，我们提出了NeuS2

  • 使用可学习特征向量的多分辨率哈希表参数化神经网络编码的SDF
  • 推导了一个针对基于relu的mlp的二阶导数的简单公式，该公式可以在显着降低计算成本的情况下，以较小的内存占用实现高效的CUDA
  • 引入了一种高效的渐进式训练策略，该策略以从粗到精的方式更新哈希表特征

我们进一步将该方法扩展到多视图动态场景重建中。我们提出了一种新的增量学习策略，以有效地学习具有大运动和变形的物体的神经动态表示，而不是单独训练序列中的每一帧。虽然一般来说，这种策略效果很好，但我们观察到，当两个连续帧之间的运动相对较大时，大多数图像中未观察到的遮挡区域的预测SDF可能会卡在前一帧的学习SDF中。
为了解决这个问题，我们预测了一个全局转换，在学习新框架的表示之前大致对齐这两个框架。

总结贡献：

  • 我们提出了一种新的方法NeuS2，用于从静态和动态场景的多视图RGB输入中快速学习神经表面表示，该方法在实现前所未有的重建质量的同时实现了最先进的速度
  • 提出了一种针对基于relu的mlp的二阶导数的简单公式，以实现GPU计算的高效并行化。
  • 提出了一种从粗到细的多分辨率哈希编码学习的渐进式训练策略，以实现更快更好的训练收敛性。
  • 我们设计了一种具有新的全局变换预测组件的增量学习方法，用于以高效和稳定的方式重建具有大运动的长序列(例如2000帧)。
  • Multi-view Stereo.传统的多视图三维重建方法可分为基于深度和基于体素的方法。
    • 基于深度的方法[5,13,14,52]通过识别图像之间的点对应关系来重建点云。然而，对应匹配的准确性严重影响重构的质量。
    • 基于体素的方法[11,6,54]通过使用光度一致性标准从多视图图像中恢复体素网格中的占用率和颜色，避开了显式对应匹配的困难。然而，由于体素网格的高内存消耗，这些方法的重建受到低分辨率的限制。
  • Classical Multi-view 4D Reconstruction.在多视图四维重建中，大量的工作使用预先计算的可变形模型，然后将其拟合到多视图图像中。相比之下，我们的方法不依赖于预先计算的模型，可以重建详细的结果，并处理拓扑变化。与我们的工作最相关的也是一种无模型方法。他们利用RGB和深度输入为每帧重建高质量的点云，然后产生时间相干几何。相反，我们只需要RGB作为输入，并且可以在每帧20秒内以端到端方式学习每帧的高质量几何形状和外观。
  • Neural Implicit Representations
    • NeRF[36]在新的视图合成任务中显示了高质量的结果，但由于几何表示缺乏表面约束，它无法提取高质量的表面。
    • Neus将3D表面表示为SDF，用于高质量的几何重建。但是，Neus的训练速度很慢，而且只适用于静态场景。
    • 相反，我们的方法要快100倍，当应用于动态场景重建时，可以进一步加速到每帧20秒
    • 一些基于nerf的作品[50,58,37]引入了voxelgrid特征来表示快速训练的3D属性。然而，这些方法不能提取高质量的表面，因为它们继承了体积密度场作为NeRF的几何表示[36]。
    • 相比之下，我们的方法可以实现高质量的表面重建和快速训练。对于动态场景建模，许多作品[59,41,46,42,29,65,27]提出将4D场景分解为共享规范空间和每帧可变形场
    • [12]表示具有时间感知体素特征的4D场景。[30]提出了一种用于快速动态场景学习的静态到动态学习范式。[26]提出了一种基于网格的逐帧高效重建辐射场的方法。[61]提出了一种新颖的傅立叶八叉树方法将动态场景压缩到一个模型中。这四种方法都集中在新颖的视图合成上，因此，它们并不是为了重建高质量的表面而设计的，这与我们获得高质量的表面几何和外观模型的目标不同。虽然这些工作提高了动态场景的训练效率，但训练仍然很耗时。此外，这些方法不能处理大的运动，只能重建中等质量的表面
    • 在人类行为建模中的一些工作[57,32,44,8,66,39,20,45,25,63]可以通过引入可变形模板作为先验来建模大型动作。相比之下，我们的方法可以处理大的移动，不需要可变形的模板，因此，不局限于特定的动态对象。此外，我们可以在每帧20秒的时间内学习动态场景的高质量表面。
    • Instant-NSR[71]提出了一种人体建模和渲染的方法。它首先为每一帧重建一个神经表面表示;然后应用非刚性变形获得时间相干网格序列。我们的工作主要集中在第一部分，即动态场景的快速重建，我们利用两个连续帧之间的时间一致性来加速动态表示的学习。因此，我们的工作与[71]是正交的，可以作为第一步整合到[71]中。
  • Concurrent Work
    • Voxurf[64]提出了一种基于体素的表面表示，用于快速多视图三维重建。虽然它在基线上实现了20倍的加速(即news[62])，但我们提出的方法比Voxurf快3倍以上，并且与他们论文中报道的Voxurf结果相比，实现了更好的几何质量。
    • Neuralangelo[28]提出了一种利用多分辨率哈希网格和数值梯度计算进行神经表面重建的新方法。它可以在牺牲训练成本的同时，通过多个精致的设计从多视图图像中获得密集和高保真的大规模场景几何重建结果，比我们的速度慢100倍。
    • 此外，Voxurf和Neuralangelo不是为动态场景重建而设计的。
    • 最后，Unbiased4d[22]通过扩展弯曲射线的NeuS公式，提出了一种单眼动态表面重建方法。与我们的方法形成鲜明对比的是，他们的重点在于证明在光线弯曲和具有挑战性的单目环境下也能保持无偏性，而不是在最快的速度下尽可能高的质量。

Background

Neus
给定标定过的静态场景多视图图像，NeuS[62]隐式地将场景的表面和外观表示为带符号的距离场$f(\mathbf{x}):\mathbb{R}^3\to \mathbb{R}$和辐射场$c(\mathbf{x},\mathbf{v}):\mathbb{R}^3\times\mathbb{S}^2\to\mathbb{R}^3$，其中x表示三维位置，$\textbf{v}\in\mathbb{S}^{2}$表示观看方向。通过提取$\text{SDF }\mathcal{S}=\{\mathbf{x}\in\mathbb{R}^3|f(\mathbf{x})=0\}$的零水平集，即可得到目标表面S。
为了将物体渲染成图像，Neus利用了体渲染。具体来说，对于图像的每个像素，我们采样点$\{\mathbf{p}(\mathbf{t_i})=\mathbf{o}+t_i\mathbf{v}|i=0,1,\ldots,n-1\}$，其中o为相机中心，v为观察方向。通过累积基于sdf的密度和样本点的颜色，我们可以计算光线的颜色。由于渲染过程是可微的，NeuS可以从多视图图像中学习符号距离场f和亮度场c。然而，训练过程非常缓慢，在单个GPU上需要大约8个小时。

InstantNGP
为了克服deep基于坐标的mlp训练时间慢的问题，这也是导致Neus性能缓慢的主要原因，最近，Instant-NGP[37]提出了一种多分辨率哈希编码，并证明了其有效性。具体来说，Instant-NGP假设要重建的对象在多分辨率体素网格中有界。每个分辨率的体素网格被映射到具有固定大小的可学习特征向量数组的哈希表。
对于一个3D位置$\mathrm{x\in\mathbb{R}^3}$，它在每一层得到一个哈希编码$h^i(\mathbf{x})\in\mathbb{R}^d$ (d是特征向量的维数，$i=1,…,L$)通过插值在这一层的周围体素网格上分配的特征向量。然后将所有L级别的哈希编码连接为多分辨率哈希编码$h(\mathbf{x})=\{h^i(\mathbf{x})\}_{i=1}^L\in \mathbb{R}^{L\times d}.$。除了哈希编码，训练加速的另一个关键因素是整个系统的CUDA实现，它利用了GPU的并行性。虽然运行时间得到了显著改善，但在几何重建精度方面，Instant-NGP仍然没有达到Neus的质量。

Challenges.
考虑到以上讨论，人们可能会问，Neus[62]和InstantNGP[37]的天真组合是否可以将两个世界的优点结合起来，即高的3D表面重建质量和高效的计算。我们强调，要实现像Instant-NGP[37]一样快的训练，同时实现像Neus[62]一样高质量的重建，绝非易事。具体来说，为了保证高质量的表面学习，Neus[62]中使用的Eikonal约束是必不可少的，如图2和图1，及补充材料。将Eikonal损失添加到基于cuda的mlp (Instant-NGP快速训练的关键因素[37])的关键挑战是如何有效地计算反向传播的二阶导数。

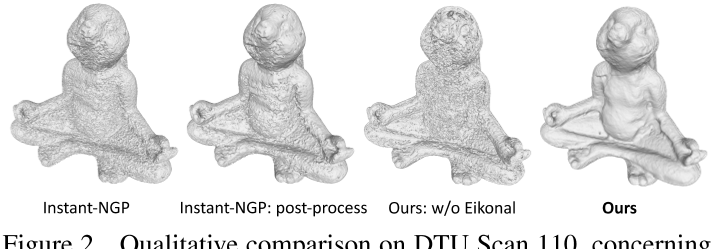
image.png

image.png

InstantNSR[71]通过使用有限差分近似二阶导数解决了这一问题，这种方法存在精度问题，并且可能导致训练不稳定。相反，我们提出了一种简单、精确、高效的针对mlp的二阶导数公式(第4.2节)，从而实现了快速、高质量的重建。我们的方法相对于Instant-NSR的优势见表1和图4所示。

image.png

image.png

对于动态场景重建，有两个关键的挑战:如何利用时间信息进行加速，以及如何处理具有大运动和变形的长序列。为了解决这些问题，我们首先提出了一种增量训练策略，利用两个连续帧共享的几何和外观信息的相似性，从而实现更快的收敛(第5.1节)。为了处理大的运动和变形，我们提出了一种新的全局变换预测组件，它可以防止预测的SDF训练陷入局部最小值。此外，它可以在小体积中绑定动态序列以节省内存并提高重建精度(第5.2节)。

Static Neural Surface Reconstruction

我们首先展示了我们的公式如何有效地从校准的多视图图像中学习静态场景的符号距离场(见图3a)。为了加速训练过程，我们首先演示了如何结合多分辨率哈希编码[37]来表示场景的SDF，以及如何应用体渲染将场景渲染成图像(第4.1节)。接下来，我们推导了针对基于relu的mlp的二阶导数的简化表达式，该表达式可以在定制的CUDA内核中有效地并行化(第4.2节)。最后，我们采用渐进式训练策略来学习多分辨率哈希编码，这导致更快的训练收敛和更好的重建质量(第4.3节)。

image.png

Volume Rendering of a Hash-encoded SDF

对于每个3D位置x，我们将其映射到具有可学习哈希表项Ω的多分辨率哈希编码$h_{\Omega}(\mathbf{x})$。由于$h_{\Omega}(\mathbf{x})$是空间位置的信息编码，因此将x映射到其SDF和颜色c的mlp可以非常浅，这将导致更有效的渲染和训练，而不会影响质量。

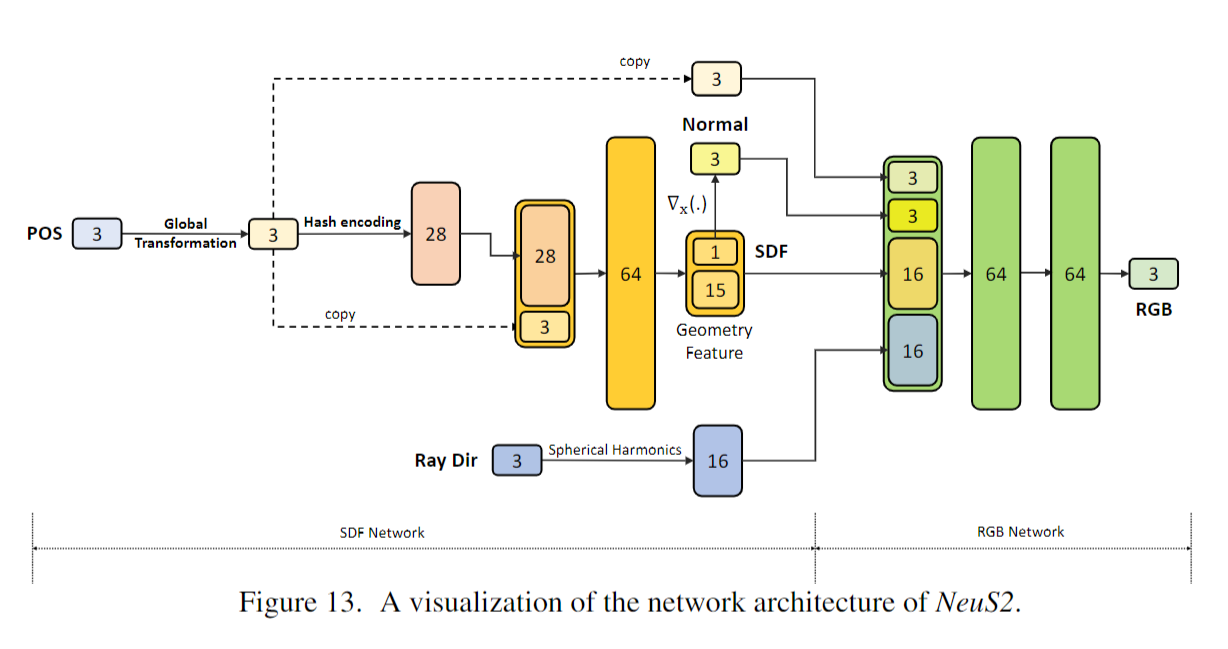
image.png

SDF Network.
$(d,\mathbf{g})=f_\Theta(\mathbf{e}),\quad\mathbf{e}=(\mathbf{x},h_\Omega(\mathbf{x})).$ Eq.1

权重为$\Theta$，以3D位置x及其哈希编码$h_{\Omega}(\mathbf{x})$作为输入，并输出SDF值d和几何特征向量$\mathbf{g}\in\mathbb{R}^{15}.$ Concatenating位置作为几何初始化[4]，导致更稳定的几何学习。

Color Network.
$\mathbf{n}=\nabla_{\mathbf{x}}d.$ Eq.2 法向$\nabla_{\mathbf{x}}d$表示SDF相对于x的梯度。
$\mathbf{c}=c_\Upsilon(\mathbf{x},\mathbf{n},\mathbf{v},d,\mathbf{g}),$ Eq.3预测了x的颜色c。

Volume Rendering.
为了渲染图像，我们采用了Neus的无偏体渲染[62]。此外，我们采用了在InstantNGP中使用的射线推进加速策略[37]。更多细节请参见support文档

Supervision
为了训练NeuS2，我们最小化渲染像素$\hat{C}_i$$i\in\{1,…,m\}$和相应的地面真值像素$C_{i}$之间的色差，无需任何3D监督。其中，m表示训练过程中的批大小。我们还使用了Eikonal项[15]来正则化学习到的带符号距离域，从而导致我们的最终损失为：$\mathcal{L}=\mathcal{L}_{\mathrm{color}}+\beta\mathcal{L}_{\mathrm{eikonal}},$ Eq.4

  • $\begin{aligned}\mathcal{L}_{\mathrm{color}}=\frac{1}{m}\sum_{i}\mathcal{R}(\hat{C}_{i},C_{i}),\end{aligned}$
  • $\mathcal{L}_{\mathrm{eikonal}}=\frac{1}{mn}\sum_{k,i}(||\mathbf{n}_{k,i}||-1)^{2}.$
    • k为沿着射线的第k个采样点$k\in\{1,…,n\}$
    • n为采样点数量
    • $\mathrm{n}_{k,i}$为采样点的法向量

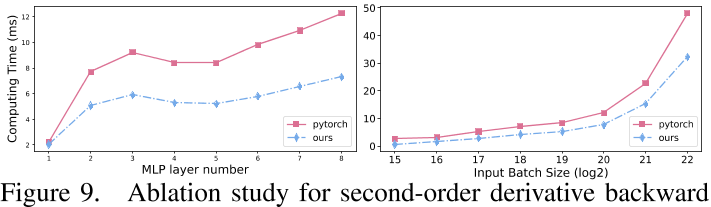
Efficient Handling of Second-order Derivatives

为了避免学习框架带来的计算开销，我们在CUDA中实现了整个系统。与Instant-NGP[37]在优化过程中只需要一阶导数相比，我们必须计算与输入到颜色网络$c_{\Upsilon}$(Eq. 3)的正态项$\mathbf{n}=\nabla_{\mathbf{x}}d$(Eq. 2)和Eikonal损失项$\mathcal{L}_{\mathrm{eikonal}}.$相关的参数的二阶导数。

二阶导数。为了加快计算速度，我们直接使用简化公式计算它们，而不是使用PyTorch的计算图[43]。具体来说，我们使用链式法则计算哈希表参数Ω和SDF网络参数Θ的二阶导数

  • $\frac{\partial\mathcal{L}}{\partial\Omega}=\frac{\partial\mathcal{L}}{\partial\mathbf{n}}(\frac{\partial\mathbf{e}}{\partial\mathbf{x}}\frac{\partial\frac{\partial d}{\partial\mathbf{e}}}{\partial\mathbf{e}}\frac{\partial\mathbf{e}}{\partial\Omega}+\frac{\partial d}{\partial\mathbf{e}}\frac{\partial\frac{\partial\mathbf{e}}{\partial\mathbf{x}}}{\partial\Omega})$ Eq.5
  • $\frac{\partial\mathcal{L}}{\partial\Theta}=\frac{\partial\mathcal{L}}{\partial\mathbf{n}}(\frac{\partial\mathbf{e}}{\partial\mathbf{x}}\frac{\partial\frac{\partial d}{\partial\mathbf{e}}}{\partial\Theta}+\frac{\partial d}{\partial\mathbf{e}}\frac{\partial\frac{\partial\mathbf{e}}{\partial\mathbf{x}}}{\partial\Theta})$ Eq.6

注意颜色网络$c_{\Upsilon}$只接受n作为输入，所以我们不需要计算颜色网络参数$\Upsilon$的二阶梯度。公式14和15的推导在补充文档中。
为了加快公式14和15的计算速度，我们发现基于relu的mlp可以大大简化上述项，从而减少计算开销。下面，我们将对此进行更详细的讨论，并在补充文件中提供该命题的证明。我们首先介绍如下一些有用的定义。

  • 定义1
    • 给定一个基于ReLU的MLP f，其中L个隐藏层以$x\in\mathbb{R}^{d}$为输入，它计算输出$y =H_{L}g(H_{L-1}\ldots g(H_{1}x))$，其中$\begin{aligned}H_l\in\mathbb{R}^{n_l}\times\mathbb{R}^{n_{l-1}}\end{aligned}$,$l \in \{1,\ldots,L\}$为层索引，g为ReLU函数。我们定义$P_l^j\in\mathbb{R}^{n_{l-1}}\times\mathbb{R}^1$, $\begin{aligned}S_l^i\in\mathbb{R}^1\times\mathbb{R}^{n_l}\end{aligned}$为：
      • $P_l^j=G_lH_{l-1}\ldots G_2H_1^{(_,j)}$
      • $S_l^i=H_L^{(i,_)}G_L\ldots H_{l+1}G_{l+1}$ Eq.7
        • $H_1^{(-,j)}$是$H_{1}$的第j列，$H_{L}^{(i,_)}$是$H_{L}$的第i行
        • $G_l=\begin{cases}1,H_{l-1}\ldots g(H_1x)>0\\0,otherwise\end{cases}$
    • 现在可以定义基于relu的MLP关于其输入层和中间层的二阶导数。
  • 定理1：基于relu的MLP二阶导数
    • 给定一个基于ReLU的MLP f 有L个隐藏层，与定义2中定义相同。MLP f的二阶导数为:
      • $\frac{\partial\frac{\partial y}{\partial x}_{(i,j)}}{\partial H_l}=(P_l^jS_l^i)^T,$ $\frac{\partial^2y}{\partial\mathbf{x}^2}=0$ Eq.8
        • $\frac{\partial y}{\partial x}_{(i,j)}$ 是$\frac{\partial\overline{y}}{\partial x}$的矩阵元素(i,j)
    • 回到我们最初的二阶导数(公式14和15)，根据定理2，我们得到$\frac{\partial\frac{\partial d}{\partial\mathbf{e}}}{\partial\mathbf{e}}=0.$。因为$\frac{\partial\mathbf{e}}{\partial\mathbf{x}}$与$\Theta$无关，所以我们有$\frac{\partial\frac{\partial\mathbf{e}}{\partial\mathbf{x}}}{\partial\Theta}=0.$。结果是下面的简化形式:
      • $\frac{\partial\mathcal{L}}{\partial\Omega}=\frac{\partial\mathcal{L}}{\partial\mathrm{n}}\frac{\partial d}{\partial\mathrm{e}}\frac{\partial\frac{\partial\mathbf{e}}{\partial\mathbf{x}}}{\partial\Omega}$ Eq.9
      • $\frac{\partial\mathcal{L}}{\partial\Theta}=\frac{\partial\mathcal{L}}{\partial\mathbf{n}}\frac{\partial\mathbf{e}}{\partial\mathbf{x}}\frac{\partial\frac{\partial d}{\partial\mathbf{e}}}{\partial\Theta}$ Eq.10
    • 对于二阶导数，这导致提高效率和更少的计算开销。$\frac{\partial\mathcal{L}}{\partial\Omega}$和$\frac{\partial\mathcal{L}}{\partial\Theta}$的最简单形式可以通过使用公式17替换$\frac{\partial\frac{\partial\mathbf{e}}{\partial\mathbf{x}}}{\partial\Omega}$和$\frac{\partial\frac{\partial d}{\partial\mathbf{e}}}{\partial\mathbf{\Theta}}$的项来获得。我们在图9中显示，使用Eq. 17的计算比PyTorch更有效。

image.png

Progressive Training

虽然我们高度优化的梯度计算已经改善了训练时间，但我们发现在训练收敛性和速度方面仍有改进的空间。此外，我们通过经验观察到，在低分辨率下使用网格会导致数据的欠拟合，其中几何重建是光滑的，缺乏细节，而在高分辨率下使用网格会导致过拟合，导致结果的噪声和伪像增加。因此，我们引入一种渐进式训练方法，通过逐渐增加空间网格编码的带宽，表示为:

$h_{\Omega}(\mathbf{x},\lambda)=\big(w_{1}(\lambda)h_{\Omega}^{1}(\mathbf{x}),\ldots,w_{L}(\lambda)h_{\Omega}^{L}(\mathbf{x})\big),$ Eq.11

其中$h_{\Omega}^i$为level i 的哈希编码，每个网格编码层的权重$w_{i}$由$w_{i}(\lambda)=I[i\leq\lambda]$定义，参数λ调制应用于多分辨率哈希编码的低通滤波器的带宽。较小的参数λ导致更快的训练速度，但限制了模型模拟高频细节的能力。因此，我们初始化λ为2，然后在所有实验中每2.5%的总训练步长逐渐增加1。

Dynamic Neural Surface Reconstruction

我们已经解释了NeuS2如何能够产生高度准确和快速的静态场景重建。接下来，我们将NeuS2扩展到动态场景重建。也就是说，给定一个运动物体的多视图视频和每个视图的摄像机参数，我们的目标是学习每个视频帧中物体的神经隐式表面(见图3b)。

Incremental Training

尽管我们的静态对象重建方法可以达到很好的效率和质量，但是通过单独训练每一帧来构建动态场景仍然很耗时。然而，从一帧到另一帧的场景变化通常很小。因此，我们提出了一种增量训练策略来利用两个连续帧之间共享的几何和外观信息的相似性，从而使我们的模型能够更快地收敛。具体来说，我们像静态场景重建中一样从头开始训练第一帧，然后根据学习到的前一帧的哈希网格表示对后续帧的模型参数进行微调。使用该策略，该模型能够对目标帧的神经表示进行良好的初始化，从而显著加快其收敛速度。

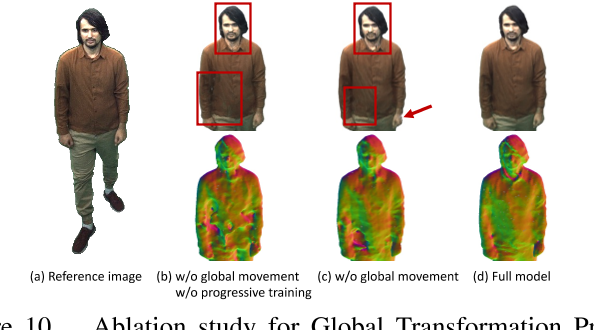
Global Transformation Prediction

我们在增量训练过程中观察到，预测的SDF很容易卡在前一帧学习到的SDF的局部极小值中，特别是当目标在相邻帧之间的移动比较大的时候。例如，当我们的模型从多视图图像中重建行走序列时，重建的表面看起来有许多孔，如图10所示。为了解决这个问题，我们提出了一个全局转换预测，在增量训练之前将目标SDF粗略地转换到一个规范空间。具体来说，我们预测了物体在两个相邻帧之间的旋转R和过渡T。对于坐标系i坐标空间中任意给定的三维位置$\mathrm{x}_i$，它被转换回前一坐标系i - 1的坐标空间，记作$\mathbf{x}_{i-1}$
$\mathbf{x}_{i-1}=R_i(\mathbf{x}_i+T_i).$ Eq.12

image.png

然后可以累积变换，将点xi转换回第一帧坐标空间中的$x_c$
$\mathbf{x}_{c}=R_{i-1}^{c}(\mathbf{x}_{i-1}+T_{i-1}^{c})=R_{i}^{c}(\mathbf{x}_{i}+T_{i}^{c}),$ Eq.13

  • $R_i^c=R_{i-1}^cR_i$
  • $T_{i}^{c}=T_{i}+R_{i}^{-1}T_{i-1}^{c}.$

全局变换预测还允许我们在小区域内对具有大移动的动态序列进行建模，而不是用大的哈希网格覆盖整个场景。由于哈希网格只需要对整个场景的一小部分进行建模，因此我们可以获得更准确的重建并降低内存成本。
值得注意的是，由于我们的方法的以下设计，我们的方法可以处理大的运动和变形，这对现有的动态场景重建方法[59]，[46]来说是具有挑战性的：
（1）全局变换预测，其解释了序列中的大的全局运动；
（2） 增量训练，学习两个相邻帧之间相对较小的可变形运动，而不是学习从每个帧到公共规范空间的相对较大的运动。
我们将增量训练与全局变换预测相结合作为一种端到端的学习方案来实现，如图所示。第3（b）段。在处理新帧时，我们首先独立预测全局变换，然后将模型的参数和全局变换一起微调，以有效地学习神经表示。

实验

3090 GPU

  • Static Scene Reconstruction
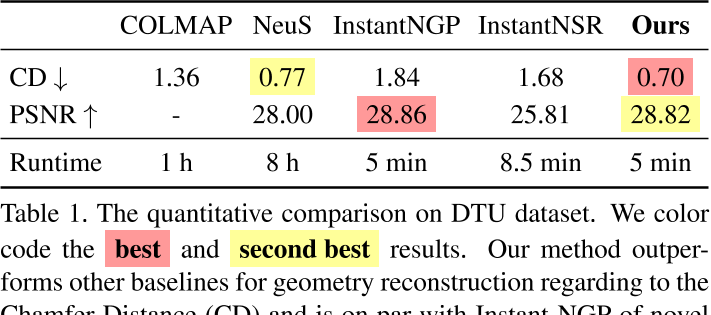
    • 数据集：DTU
    • Baseline：Neus、InstantNGP、Instant-NSR、Voxurf
    • quantitative：Chamfer Distance、PSNR
    • qualitative
  • Dynamic Scene Reconstruction
    • 数据集：
      • Synthetic Scenes：NeRF共享的乐高场景、Artemis提供的狮子序列、RenderPeople中的人类角色
      • Real Scenes：Dynacap数据集中选择了三个序列
    • Baseline：D-NeRF、TiNeuVox
    • quantitative：Chamfer Distance、PSNR
    • qualitative
  • Ablation
    • 高效二阶导反向传播计算 VS Pytorch
    • with or without :
      • GTP
      • PT

环境配置

PyTorch 1.11.0 | Python 3.8(ubuntu20.04) | Cuda 11.3

升级cmake 3.18以上
sudo apt-get install xorg-dev

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
git clone --recursive https://github.com/19reborn/NeuS2
cd NeuS2

cmake . -B build
cmake --build build --config RelWithDebInfo -j 

# conda create env
conda create -n neus2 python= your image
conda activate neus2
pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple
commentjson~=0.9.0
imageio~=2.16.0
numpy~=1.21.2
pybind11~=2.7.1
scipy~=1.7.1
tqdm~=4.62.2
opencv-python~=4.5.5.62
trimesh
tensorboard
https://pypi.tuna.tsinghua.edu.cn/simple

# install pytorch and pytorch3d
pip install torch
pip install "git+https://github.com/facebookresearch/pytorch3d.git@stable"

pytorch3d/INSTALL.md at main · facebookresearch/pytorch3d (github.com)

运行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# run c++
./build/testbed --scene ${data_path}/transform.json
## eg:
./build/testbed --scene ./data/neus/dtu_scan114/transform_train.json -n dtu.json --no-gui
## questions:
no output

# run python
python scripts/run.py --scene ${data_path}/transform.json --name ${your_experiment_name} --network ${config_name} --n_steps ${training_steps}
## eg: autodl-tmp/NeuS2/data/neus/dtu_scan114/transform_train.json
python scripts/run.py --scene ./data/neus/dtu_scan114/transform_train.json --name neus --network dtu.json --n_steps -1

# 数据转换
python tools/data_format_from_neus.py --dataset_name dtu_scan114 --copy_image
or 
python tools/data_format_from_neus.py --dataset_all --copy_image

Miku

1
python scripts/run.py --scene ./data/neus/Miku/transform_train.json --name Miku --network dtu.json --n_steps 20000

neuspp —> womask

1
python scripts/run.py --scene ./data/neus/Miku/transform_train.json --name Miku --network womask.json --n_steps -1

Welcome to my other publishing channels