PermutoSDF

Title	PermutoSDF: Fast Multi-View Reconstruction with Implicit Surfaces using Permutohedral Lattices
Author	Radu Alexandru Rosu, Sven Behnke
Conf/Jour	CVPR
Year	2023
Project	PermutoSDF (radualexandru.github.io)
Paper	PermutoSDF: Fast Multi-View Reconstruction with Implicit Surfaces using Permutohedral Lattices (readpaper.com)

创新：用permutohedral lattice替换voxel hash encoding

• simplex,3D中的单纯形就是正四面体

• 几何细节光滑，通过曲率损失来实现

• 带Lipschitz常数的颜色MLP来训练，使得高频颜色与高频几何特征相匹配
  • ref : [PDF] Learning Smooth Neural Functions via Lipschitz Regularization-论文阅读讨论-ReadPaper
  • $y=\sigma(\widehat{W}_ix+b_i),\quad\widehat{W}_i=m\left(W_i,\text{softplus}\left(k_i\right)\right)$

Conclusion

We proposed a combination of implicit surface representations and hash-based encoding methods for the task of reconstructing accurate geometry and appearance from unmasked posed color images.

We improved upon the voxel-based hash encoding by using a permutohedral lattice which is always faster in training and faster for inference in three and higher dimensions. Additionally, we proposed a simple regularization scheme that allows to recover fine geometrical detail at the level of pores毛孔 and wrinkles. Our full system can train in ≈ 30 min on an RTX 3090 GPU and render in real-time using sphere tracing. We believe this work together with the code release will help the community in a multitude of other tasks that require modeling signals using fast local features.

AIR

To NGP_MHE and Neus_SDF
We propose improvements to the two areas by replacing the voxel hash encoding with a permutohedral lattice置换面体晶格 which optimizes faster, especially for higher dimensions.

Accurate reconstruction geometry and appearance of scenes is an important component of many computer vision tasks. Recent Neural Radiance Field (NeRF)-like models represent the scene as a density and radiance field and, when supervised with enough input images, can render photorealistic novel views.

Speed：Works like INGP [18] further improve on NeRF by using a hash-based positional encoding which results in fast training and visually pleasing results. However, despite the photorealistic renderings, the reconstructed scene geometry can deviate severally from the ground-truth重建场景的几何表现不是很好 For example, objects with high specularity高镜面 or view-dependent effects视觉相关影响 are often reconstructed as a cloud of low density; untextured regions can have arbitrary density in the reconstruction.

• 无法处理高镜面、视觉相关的影响造成的低密度点云
• 无纹理区域在重建中密度随机

SDF：Another line of recent methods tackles the issue of incorrect geometry by representing the surfaces of objects as binary occupancy or Signed Distance Function (SDF). This representation can also be optimized with volumetric rendering techniques that are supervised with RGB images. However, parametrization of the SDF as a single fully-connected Multi-Layer Perceptron (MLP) often leads to overly smooth geometry and color.

• SDF参数化为单个全连接MLP通常导致几何和颜色过于平滑

In this work, we propose PermutoSDF, a method that combines the strengths of hash-based encodings and implicit surfaces. We represent the scene as an SDF and a color field, which we render using unbiased volumetric integration(Neus中提出的体积积分方法). A naive combination of these two methods would fail to reconstruct accurate surfaces however, since it lacks any inductive bias for the ambiguous cases like specular or untextured surfaces. 简单叠加NGP和Neus，依然对无纹理和镜面等模糊情况，缺乏任何归纳偏差
Attempting to regularize the SDF with a total variation loss or a curvature loss will produce a smoother geometry at the expense of losing smaller details. 如果使用总变异损失和曲率损失，几何更光滑，但是代价是丢失更小的细节

In this work:

In this work, we propose a regularization scheme that ensures both smooth geometry where needed and also reconstruction of fine details like pores and wrinkles 本文正则化方案，确保所需的平滑几何形状及可以重建毛孔、皱纹等细节
Furthermore, we improve upon the voxel hashing method of INGP by proposing permutohedral lattice hashing. The number of vertices per simplex (triangle, tetrahedron, . . . ) in this data structure scales linearly with dimensionality instead of exponentially as in the hyper-cubical voxel case 每个simplex的定点数随着维度数线性缩放，而不是指数缩放，We show that the permutohedral lattice performs better than voxels for 3D reconstruction and 4D background estimation.
Main contribution：

• a novel framework for optimizing neural implicit surfaces based on hash-encoding,
• an extension of hash encoding to a permutohedral lattice which scales linearly with the input dimensions and allows for faster optimization, and
• a regularization scheme that allows to recover accurate SDF geometry with a level of detail at the scale of pores and wrinkles.

Related Work

• Classical Multi-View Reconstruction
  • Multi-view 3D reconstruction has been studied for decades. The classical methods can be categorized as either depth map-based or volume-based
    • Depth map methods like COLMAP [25] reconstruct a depth map for each input view by matching photometrically consistent patches. The depth maps are fused to a global 3D point cloud and a watertight水密 surface is recovered using Poisson泊松 Reconstruction [12]. While COLMAP can give good results in most scenarios, it yields suboptimal次优 results on non-Lambertian surfaces.
    • Volume-based approaches fuse the depth maps into a volumetric structure (usually a Truncated Signed Distance Function) from which an explicit surface can be recovered via the marching cubes algorithm [15]. Volumetric methods work well when fusing multiple noisy depth maps but struggle with reconstructing thin surfaces and fine details
• NeRF Models
  • A recent paradigm shift in 3D scene reconstruction has been the introduction of NeRF
  • NeRFs represent the scene as density and radiance fields, parameterized by a MLP. Volumetric rendering is used to train them to match posed RGB images. This yields highly photorealistic renderings with view-dependent effects. However, the long training time of the original NeRF prompted a series of subsequent works to address this issue.
• Accelerating NeRF
  • Two main areas were identified as problematic: the large number of ray samples that traverse empty space and the requirement to query a large MLP for each individual sample.
  • [PDF] Neural Sparse Voxel Fields uses an octree to model only the occupied space and restricts samples to be generated only inside the occupied voxels. Features from the voxels are interpolated and a shallow MLP predicts color and density. This achieves significant speedups but requires complicated pruning剪枝 and updating of the octree structure.
  • DVGO similarly models the scene with local features which are stored in a dense grid that is decoded by an MLP into view-dependent color.
  • Plenoxels completely removes any MLP and instead stores opacity and spherical harmonics (SH) coefficients at sparse voxel positions.
  • Instant Neural Graphics Primitives proposes a hash-based encoding in which ray samples trilinearly interpolate features between eight positions from a hash map. A shallow MLP implemented as a fully fused CUDA kernel predicts color and density. Using a hash map for encoding has the advantage of not requiring complicated mechanisms for pruning or updating like in the case of octrees.
  • In our work, we improve upon INGP by proposing a novel permutohedral lattice-based hash encoding, which is better suited for interpolating in high-dimensional spaces. We use our new encoding to reconstruct accurate 3D surfaces and model background as a 4D space.
• Implicit Representation
  • Other works have focused on reconstructing the scene geometry using implicit surfaces.
  • SDFDiff discretizes离散化 SDF values on a dense grid and by defining a differentiable shading function can optimize the underlying geometry. However, their approach can neither recover arbitrary color values nor can it scale to higher-resolution geometry.
  • IDR and DVR represent the scene as SDF and occupancy map, respectively分别, and by using differentiable rendering can recover high-frequency geometry and color. However, both methods require 2D mask supervision for training which is not easy to obtain in practice.
  • In order to remove the requirement of mask supervision
    • UNISURF optimizes an binary occupancy function through volumetric rendering.
    • VolSDF extends this idea to SDFs.
    • NeuS analyzes the biases caused by using volumetric rendering for optimizing SDFs and introduces an unbiased and occlusion-aware weighting scheme无偏碰撞的权重方案 which allows to recover more accurate surfaces.
  • In this work, we reconstruct a scene as SDF and color field without using any mask supervision. We model the scene using locally hashed features in order to recover finer detail than previous works. We also propose several regularizations which help to recover geometric detail at the level of pores and wrinkles.

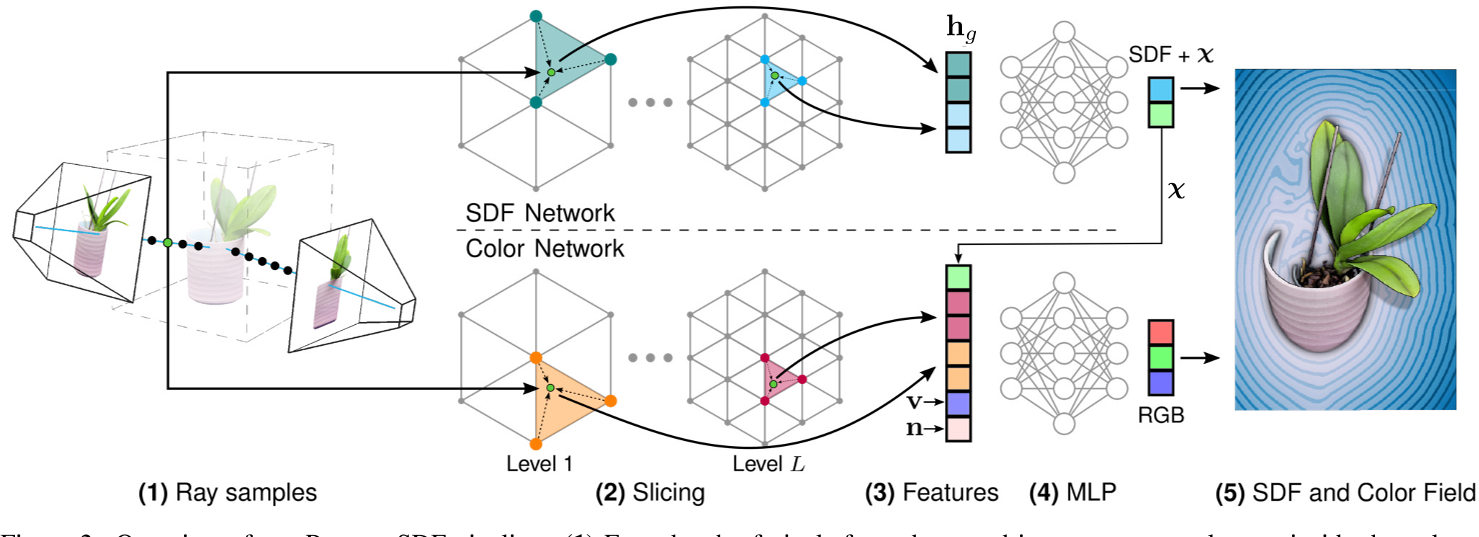
Method Overview

Given a series of images with poses $\{\mathcal{I}_{k}\}$, our task is to recover both surface S and appearance of the objects within.
We define the surface S as the zero level set of an SDF:$\mathcal{S}=\{\mathrm{x}\in\mathbb{R}^3|g(\mathrm{x})=0\}.$

$SDF,\chi = g(\operatorname{enc}(\mathbf{x};\theta_g);\Phi_g)$

• 输入坐标x
  $Color = c(\mathbf{h}_c,\mathbf{v},\mathbf{n},\chi;\Phi_c)$
• $\mathbf{h}_c=\operatorname{enc}(\mathbf{x};\theta_c)$
• $\mathbf{v}$为观察方向
• $\mathbf{n}$为法向方向，sdf梯度
• a learnable geometric feature $\chi$ which is output by the sdf network

Note, that using two separate networks is crucial as we want to regularize each one individually in order to recover high-quality geometry.

Permutohedral Lattice SDF Rendering

We now detail each network, the permutohedral lattice, and our training methodology.

Volumetric Rendering

$\hat{C}(\mathbf{p})=\int_{t=0}^{+\infty}w(t)c(\mathbf{p}(t),\mathbf{v},\mathbf{n},\chi;\Phi_c),$

$\rho(t)=\max\left(\frac{-\frac{\mathrm{d}\psi_s}{\mathrm{d}t}(g(\mathbf{p}(t);\Phi_g))}{\psi_s(g(\mathbf{p}(t);\Phi_g))},0\right),$$\psi_s(x)=\frac{1}{1+e^{-ax}}$

$w(t)=T(t)\rho(t),\mathrm{~where~}T(t)=\exp\left(-\int_0^t\rho(u)\mathrm{d}u\right)$

Hash Encoding with Permutohedral Lattice

In order to facilitate learning of high-frequency details, INGP [18] proposed a hash-based encoding which maps a 3D spatial coordinate to a higher-dimensional space. The encoding maps a spatial position x into a cubical grid and linearly interpolates features from the hashed eight corners of the containing cube. A fast CUDA implementation interpolates over various multi-resolutional grids in parallel. The hash map is stored as a tensor of L levels, each containing up to T feature vectors with dimensionality F .

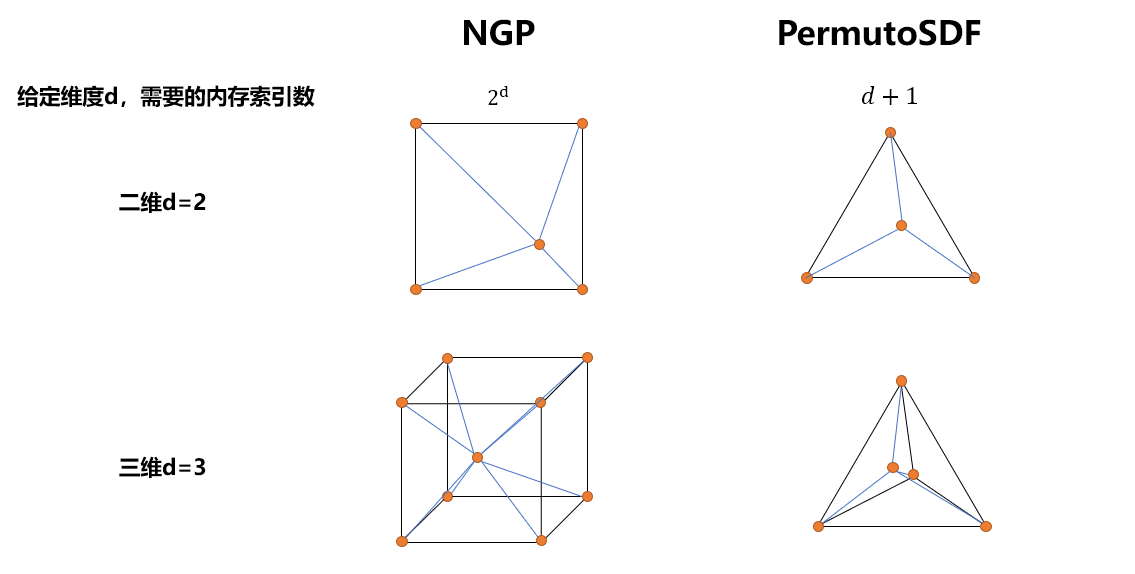
The speed of the encoding function is mostly determined by the number of accesses to the hash map as the operations to determine the eight hash indices are fast. Hence, it is of interest to reduce the memory accesses required to linearly interpolate features for position x. By using a tetrahedral lattice instead of a cubical one, memory accesses can be reduced by a factor of two as each simplex has only four vertices instead of eight. This advantage grows for higher dimensions when using a permutohedral lattice [1].[PDF] Fast High‐Dimensional Filtering Using the Permutohedral Lattice-论文阅读讨论-ReadPaper

The permutohedral lattice divides the space into uniform simplices均匀单纯形 which form triangles and tetrahedra in 2D and 3D, respectively. The main advantage of this lattice is that given dimensionality d the number of vertices per simplex is d+1, which scales linearly instead of the exponential growth $2^{d}$ for hyper-cubical voxels. This ensures a low number of memory accesses to the hashmap and therefore fast optimization.

Given a position x, the containing simplex can be obtained in $O(d^{2})$. Within the simplex, barycentric coordinates are calculated and d-linear interpolation is performed similar to INGP.
Similarly to INGP, we slice from lattices at multiple resolutions and concatenate the results. The final output is a high-dimensional encoding $h = enc(x; θ)$ of the input x given lattice features θ.

4D Background Estimation

For modeling the background, we follow the formulation of NeRF++ which represents foreground volume as a unit sphere and background volume by an inverted sphere.

Points in the outer volume are represented using 4D positions (x′, y′, z′, 1/r) where (x′, y′, z′) is a unit-length directional vector and 1/r is the inverse distance.
对4D的背景进行编码时，a cubical voxel（NGP）需要查询16个顶点的特征值，而permutohedral lattice只需要查询5个顶点的特征值
We directly use this 4D coordinate to slice from a 4-dimensional lattice and obtain multi-resolutional features. A small MLP outputs the radiance and density which are volumetrically rendered and blended with the foreground. Please note that in 4D, the permutohedral lattice only needs to access five vertices(4d+1) for each simplex while a cubical voxel would need 16($2^{4}$). Our linear scaling with dimensionality is of significant advantage in this use case.

PermutoSDF Training and Regularization

简单融合使用loss：

• $\mathcal{L}_{\mathrm{rgb}}=\sum_p\lVert\hat{C}(\mathbf{p})-C(\mathbf{p})\rVert_2^2$
• $\mathcal{L}_{\mathrm{eik}}=\sum_{x}\left(|\nabla g(\mathrm{enc}(\mathrm{x}))|-1\right)^2,$

A naive combination of hash-based encoding and implicit surfaces can yield undesirable surfaces, though. While the model is regularized by the Eikonal loss, there are many surfaces that satisfy the Eikonal constraint.
For specular or untextured areas, the Eikonal regularization doesn’t provide enough information to properly recover the surface. To address this issue, we propose several regularizations that serve to both recover smoother surfaces and more detail.

SDF Regularization—>smoother surfaces

In order to aid the network in recovering smoother surfaces in reflective or untextured areas, we add a curvature loss on the SDF
Calculating the full 3×3 Hessian matrix can be expensive; so we approximate curvature as local deviation of the normal vector. Recall that we already have the normal $n = ∇g(enc(x))$ at each ray sample since it was required for the Eikonal loss. With this normal, we define a tangent vector切向量 $η$ by cross product with a random unit vector τ such that $η = n × τ$.Given this random vector in the tangent plane, we slightly perturb our sample x to obtain $\mathrm{x}_\epsilon=\mathrm{x}+\epsilon\eta.$. We obtain the normal at the new perturbed point as $\mathbf{n}_\epsilon=\nabla g(\mathrm{enc}(\mathbf{x}_\epsilon))$ and define a curvature loss based on the dot product between the normals at the original and perturbed points:
curvature loss: $\mathcal{L}_\mathrm{curv}=\sum_x(\mathbf{n}\cdot\mathbf{n}_\epsilon-1)^2.$

物理含义：表面上相邻两点的法向量应该是平行的

Color Regularization详细解析深度学习中的 Lipschitz 条件 - 知乎 (zhihu.com)

While the curvature regularization helps in recovering smooth surfaces, we observe that the network converges to an undesirable state where the geometry gets increasingly smoother while the color network learns to model all the high-frequency detail in order to drive the $\mathcal{L}_{rgb}$ to zero. Despite lowering $\mathcal{L}_{curv}$ during optimization, the SDF doesn’t regain back the lost detail. We show this behavior in Fig. 8. Recall that the color network is defined as $Color = c(\mathbf{h}_c,\mathbf{v},\mathbf{n},\chi;\Phi_c)$, with an input encoding of $h = enc(x; θ_{c})$. We observe that all the high-frequency detail learned by the color network has to be present in the weights of the MLP $Φ_{c}$ or the hashmap table $θ_{c}$ as all the other inputs are smooth. 颜色网络学习到的高频细节都在MLP的权重$Φ_{c}$或哈希表$θ_{c}$中，因为其他所有输入$\mathbf{v},\mathbf{n},\chi$都是平滑的

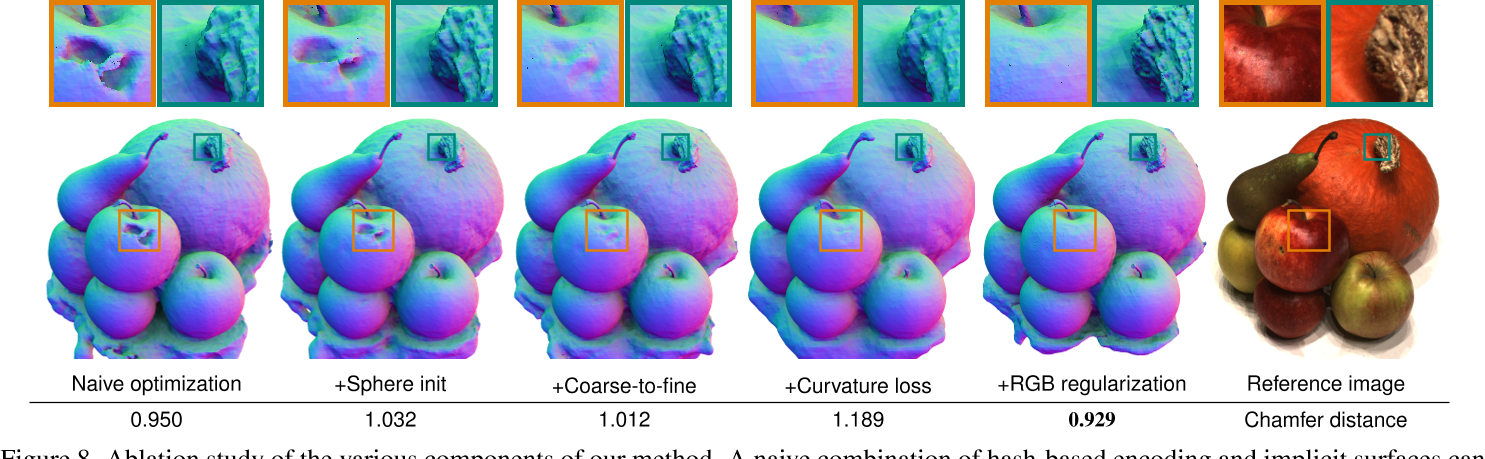
In order to recover fine geometric detail, we propose to learn a color mapping network that is itself smooth w.r.t. to its input such that large changes in color are matched with large changes in surfaces normal. Function smoothness can be studied in the context of Lipschitz continuous networks. A function f is k-Lipschitz continuous if it satisfies: $\underbrace{|f(d)-f(e)|}_{\text{change in the output}}\leq k\underbrace{|d-e|}_{\text{change in the input}}$
Intuitively, it sets k as an upper bound上限 for the rate of change of the function. We are interested in the color network being a smooth function (small k) such that high-frequency color is also reflected in high-detailed geometry. There are several ways to enforce Lipschitz smoothness on a function . Most of them impose a hard 1-Lipschitz requirement or ignore effects such as network depth which makes them difficult to tune for our use case

修改后的颜色MLP网络

The recent work of Liu et al. [PDF] Learning Smooth Neural Functions via Lipschitz Regularization-论文阅读讨论-ReadPaper provides a simple and interpretable framework for softly regularizing the Lipschitz constant of a network. Given an MLP layer $y =σ(W_{i}x+b_{i})$and a trainable Lipschitz bound $k_{i}$ for the layer, they replace the weight matrix $W_{i}$with:
$y=\sigma(\widehat{W}_ix+b_i),\quad\widehat{W}_i=m\left(W_i,\text{softplus}\left(k_i\right)\right)$

• $\text{softplus }(k_i)=\ln(1+e^{k_i})$
• the function m(.) normalizes the weight matrix by rescaling each row of $W_{i}$ such that the absolute value of the row-sum is less than or equal to softplus (ki).

import jax.numpy as jnp 
def normalization(Wi, softplus_ci): # L-inf norm
    absrowsum = jnp.sum(jnp.abs(Wi), axis=1) 
    scale = jnp.minimum(1.0, softplus_ci/absrowsum) 
return Wi * scale[:,None]

y = sigma(normalization(Wi, softplus(ci))*x + bi)

Since the product of per-layer Lipschitz constants $k_{i}$ is the Lipschitz bound for the whole network, we can regularize it using:

$\mathcal{L}_{\mathrm{Lipschitz}}=\prod_{l}^{i=1}\text{softplus}\left(k_{i}\right).$

In addition to regularizing the color MLP, we also apply weight decay of 0.01 to the color hashmap $θ_{c}$.

Lipschitz in DL

详细解析深度学习中的 Lipschitz 条件 - 知乎 (zhihu.com)

$\underbrace{|f(d)-f(e)|}_{\text{change in the output}}\leq k\underbrace{|d-e|}_{\text{change in the input}}$
$||f(x,y_1)-f(x,y_2)||\leq L||y_1-y_2||,$

Lipschitz continuous含义：存在一个实数 L ，使得对于函数f(x) 上的每对点，连接它们的线的斜率的绝对值不大于这个实数L。最小的 L 称为该函数的 Lipschitz 常数，意味着函数被一次函数上下夹逼。

eg：$f:[-3,7]\to\mathbb{R},f(x)=x^2:$ 符合利普希茨连续条件, L=14

(Bi-Lipschitz continuous $\begin{aligned}\frac{1}{L}||y_1-y_2||\leq||f(x,y_1)-f(x,y_2)||\leq L||y_1-y_2||,\end{aligned}$)

$\left\{\begin{array}{c}f(y)\leq f(x)+L||y-x||\\f(y)\geq f(x)-L||y-x||\end{array}\right.$
可以看出，x确定后，f(y) 被一个一次函数bound在一定的范围内

[PDF] Learning Smooth Neural Functions via Lipschitz Regularization-论文阅读讨论-ReadPaper

Training Schedule

Several scheduling considerations must be observed for our method. In Eq. 3, the sigmoid function $ψ_{s}(.)$ is parametrized with 1/a which is the standard deviation that controls the range of influence of the SDF towards the volume rendering. In NeuS 1/a is considered a learnable parameter which starts at a high value and decays towards zero as the network converges

However, we found out that considering it as a learnable parameter can lead to the network missing thin object features due to the fact that large objects in the scene dominate the gradient towards a. Instead, we use a scheduled linear decay 1/a over 30 k iterations which we found to be robust for all the objects we tested.

30k iteration前，1/a不变，30k以后，对1/a做线性衰减
100k前，loss：

In order to recover smooth surfaces, we train the first 100 k iterations using curvature loss:
$\mathcal{L}=\mathcal{L}_{\mathrm{rgb}}+\lambda_{1}\mathcal{L}_{\mathrm{eik}}+\lambda_{2}\mathcal{L}_{\mathrm{curv}}.$

后100k，loss：
For further 100 k iterations, we recover detail by removing the curvature loss and adding the regularization of the color network $λ_3 \cdot \mathcal{L}_{\mathrm{Lipschitz}}$

初始10k，从粗到精，退火哈希map的水平L(多分辨率)
In addition, we initialize our network with the SDF of a sphere at the beginning of the optimization and anneal the levels L of the hash map in a coarse-to-fine manner over the course of the initial 10 k iterations.

Acceleration

Similar to other volumetric rendering methods, a major bottleneck for the speed is the number of position samples considered for each ray. We use several methods to accelerate both training and inference.

Occupancy Grid

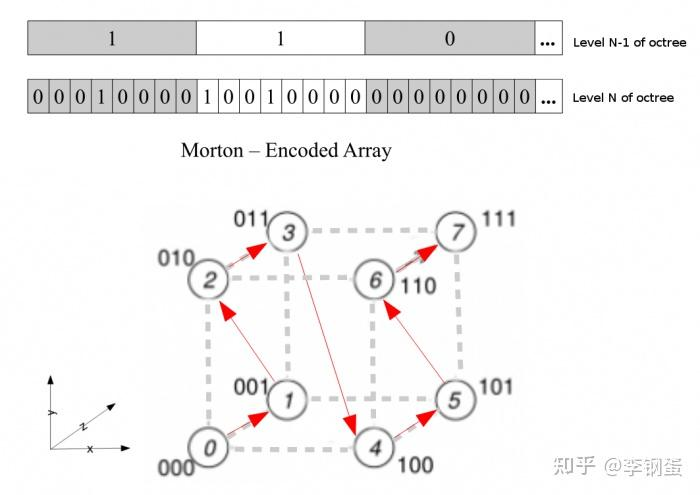
In order to concentrate more samples near the surface of the SDF and have fewer in empty space, we use an occupancy grid modeled as a dense grid of resolution $128^{3}.$ We maintain two versions of the grid, one with full precision, storing the SDF value at each voxel, and another containing only a binary occupancy bit. The grids are laid out in Morton order to ensure fast traversal. Note that differently from INGP, we store signed distance and not density in our grid. This allows us to use the SDF volume rendering equations to determine if a certain voxel has enough weight that it would meaningfully contribute to the integral Eq. 2 and therefore should be marked as occupied space.

Morton order:

• ref : Morton code理解 - 知乎 (zhihu.com)
  

Sphere Tracing

Having an SDF opens up a possibility for accelerating rendering at inference time by using sphere tracing. This can be significantly faster than volume rendering as most rays converge in 2-3 iterations towards the surface.
We create a ray sample at the first voxel along the ray that is marked as occupied. We run sphere tracing for a predefined number of iterations and march not-yet-converged samples towards the surface (indicated by their SDF being above a certain threshold). Once all samples have converged or we reached a maximum number of sphere traces, we sample the color network once and render.

Implementation Details

在CUDA kernel中实现：

• permutohedral lattices，slices in parallel from all resolutions
• The backward pass for updating the hashmap $\frac{∂h}{∂θ}$
  • We use the chain rule to backpropagate the upstream gradients as:$\frac{\partial\mathcal{L}}{\partial\mathbf{h}}\frac{\partial\mathbf{h}}{\partial\theta}.$
• the partial derivative of encoding $h = enc(x; θ_{g})$ w.r.t. to spatial position x
  • $\mathbf{n}=\nabla g(\mathrm{enc}(\mathbf{x}))$
  • Again, the chain rule is applied with the autograd partial derivative of g(.) as: $\frac{\partial g}{\partial\mathbf{h}}\frac{\partial\mathbf{h}}{\partial\mathbf{x}}$ to obtain the normal.
• Furthermore, since we use this normal as part of our loss function Leik, we support also double backward operations, i.e., we also implement CUDA kernels for $\partial(\frac{\partial\tilde{\mathcal{L}}}{\partial\mathbf{x}})/\partial\theta$ and $\partial(\frac{\partial\mathcal{L}}{\partial\mathbf{x}})\big/\partial(\frac{\partial\mathcal{L}}{\partial\mathbf{h}})$ Hence, we can run our optimization entirely within PyTorch’s autograd engine, without requiring any finite differences.
  将梯度计算和反向传播在CUDA kernel中部署，可以在Pytorch中使用autograd实现反向传播，而不需要进行有限差分获得梯度