Title	Flexible Isosurface Extraction for Gradient-Based Mesh Optimization
Author	Shen, Tianchang and Munkberg, Jacob and Hasselgren, Jon and Yin, Kangxue and Wang, Zian and Chen, Wenzheng and Gojcic, Zan and Fidler, Sanja and Sharp, Nicholas and Gao, Jun
Conf/Jour	ACM Trans. on Graph. (SIGGRAPH 2023)
Year	2023
Project	Flexible Isosurface Extraction for Gradient-Based Mesh Optimization (FlexiCubes) (nvidia.com)
Paper	Flexible Isosurface Extraction for Gradient-Based Mesh Optimization (nv-tlabs.github.io)

一种新的Marching Cube的方法

AIR

这项工作考虑了基于梯度的mesh优化，其中我们通过将其表示为标量场的等值面来迭代优化3D表面mesh，这是一种越来越普遍的应用范例，包括摄影测量，生成建模和逆物理。现有的实现采用经典的等值面提取算法，如Marching Cubes或Dual contoring;这些技术旨在从固定的、已知的区域中提取mesh，在优化设置中，它们缺乏自由度来表示高质量的特征保留mesh，或者遭受数值不稳定性的影响。我们介绍FlexiCubes，这是一种专为优化几何、视觉甚至物理目标的未知mesh而设计的等面表示。我们的主要见解是在表示中引入额外的精心选择的参数，这允许对提取的mesh几何形状和连接性进行局部灵活调整。当针对下游任务进行优化时，这些参数通过自动微分与底层标量字段一起更新。我们基于双行军立方体的提取方案来改进拓扑特性，并提供扩展以可选地生成四面体和层次自适应mesh。大量的实验验证了FlexiCubes在合成基准测试和实际应用中的应用，表明它在mesh质量和几何保真度方面提供了显着的改进。

KW：

Computing methodologies → Mesh geometry models;Shape representations; Reconstruction.
isosurface extraction, gradient-based mesh optimization, photogrammetry摄影测量, generative models

Introduction

从计算机图形学到机器人技术，表面mesh在表示、传输和生成3D几何图形方面发挥着无处不在的作用。在许多其他优点中，表面mesh提供了任意表面的简明而准确的编码，受益于高效的硬件加速渲染，并支持在物理模拟和几何处理中求解方程

然而，并不是所有的mesh都是一样的——上面的属性通常只有在高质量的mesh上才能实现。事实上，mesh中有过多的元素，suffer from self-intersections和sliver elements，或poorly捕获底层几何，可能完全不适合下游任务。因此，生成特定形状的高质量mesh非常重要，但远非微不足道，通常需要大量的手工工作。

最近算法内容创建和生成式3D建模工具的爆炸式增长导致对自动mesh生成的需求增加。事实上，制作高质量mesh的任务，传统上是熟练的技术艺术家和建模者的领域，越来越多地通过自动算法管道来解决。这些通常基于可微分mesh生成，即参数化三维表面mesh空间，并通过基于梯度的技术对各种目标进行优化。例如，逆渲染等应用[Hasselgren et al. 2022;Munkberg et al. 2022]，结构优化[Subedi et al. 2020]，生成式3D建模[Gao et al. 2022;Lin等人。2022]都利用了这个基本构建块。在一个完美的世界里，这样的应用程序将简单地对一些mesh表示执行naïve梯度下降来优化他们想要的目标。然而，从如何优化不同拓扑的mesh的基本问题到现有公式缺乏稳定性和鲁棒性导致不可挽回的低质量mesh输出，许多障碍阻碍了这种工作流程的实现。在这项工作中，我们提出了一种新的公式，使我们更接近这一目标，显着提高了各种下游任务中可微mesh生成的易用性和质量。

直接优化mesh的顶点位置很容易成为退化和局部最小值的受害者，除非非常仔细地初始化，重新mesh化和正则化使用[Liu et al. 2019;Nicolet et al. 2021;Wang et al. 2018]。因此，一个常见的范例是在空间中定义和优化标量场或符号距离函数(SDF)，然后提取一个接近该函数的水平集的三角形mesh。标量函数表示和mesh提取方式的选择对管道整体优化的性能影响很大。从标量场中提取mesh的一个微妙但重要的挑战是可能生成的mesh空间可能受到限制。正如我们稍后将展示的那样，用于提取三角形mesh的特定算法的选择直接决定了生成形状的属性。

为了解决这些问题，我们确定了mesh生成过程应该提供的两个关键属性，以便对下游任务进行简单、高效和高质量的优化:

Grad：对于mesh的微分定义良好，并且基于梯度的优化在实践中有效收敛。
Flexible：mesh顶点可以单独和局部调整，以适应表面特征，并找到具有少量元素的高质量mesh。

然而，这两个属性本质上是冲突的。增加的灵活性提供了更多的能力来表示退化几何和自交，这阻碍了基于梯度的优化的收敛。
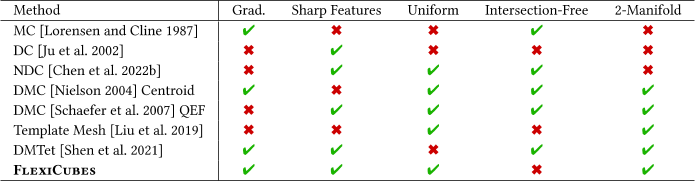
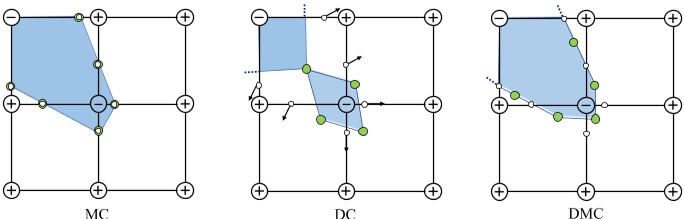
因此，现有的技术[Lorensen and Cline 1987;Remelli et al. 2020;Shen et al. 2021]通常会忽略两个属性中的一个(表1)。

例如，广泛使用的Marching Cubes过程[Lorensen and Cline 1987]并不灵活，因为顶点总是沿着固定的晶格，因此生成的mesh永远不会与非轴向对齐的尖锐特征对齐(图1)。
广义的Marching技术会使底层grid变形[Gao et al. 2020;Shen et al. 2021]，但仍然不允许调整单个顶点，导致sliver elements和不完美拟合。另一方面，双轮廓(Dual contourting) [Ju et al. 2002]因其捕捉尖锐特征的能力而广受欢迎，但缺乏grad。使用线性系统定位顶点会导致不稳定和无效的优化。第2节和表1对过去的工作进行了详细分类。

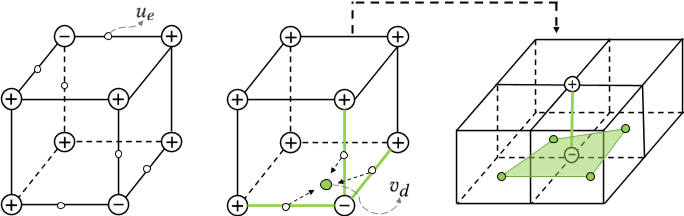
在这项工作中，我们提出了一种名为FlexiCubes的新技术，它满足了这两个期望的特性。我们的见解是采用特定的双行进立方体公式(Dual Marching Cubes)，并引入额外的自由度，以灵活地定位每个提取的顶点在其双单元内。我们仔细地约束了公式，使其在绝大多数情况下仍然产生无相交的流形和水密mesh，从而实现相对于底层mesh的良好微分(Grad.)。

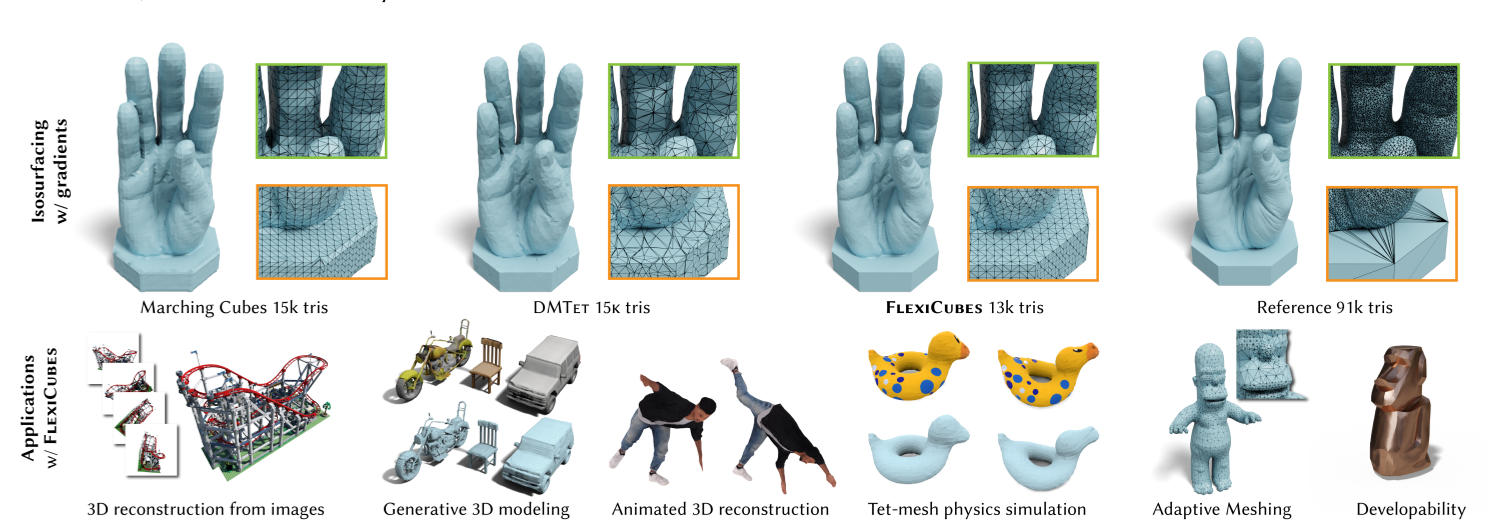
该公式最重要的特性是基于梯度的mesh优化在实践中始终成功。为了评估这种固有的经验问题，我们将本工作的重要部分用于FlexiCubes在几个下游任务上的广泛评估。具体来说，我们证明了我们的配方为各种mesh生成应用提供了显着的好处，包括反向渲染，优化物理和几何能量，以及生成3D建模。所得的mesh在低元素计数下简洁地捕获所需的几何形状，并易于通过梯度下降进行优化。此外，我们还提出了FlexiCubes的扩展，如通过分层细化自适应调整mesh分辨率，并自动对域内部进行四面体化。与过去的方法相比，基准测试和实验显示了该技术的价值，我们相信它将成为许多应用领域中高质量mesh生成的有价值的工具。

Isosurface Extraction

传统的等值面方法提取一个表示标量函数的水平集的多边形mesh，这个问题已经在多个领域得到了广泛的研究。在这里，我们回顾了特别相关的工作，并建议读者参考De Araújo等人[2015]的优秀调查(# A Survey on Implicit Surface Polygonization)，以获得全面的概述。根据De Araújo等人[2015]，我们将等表面处理方法分为三类，并将最常用的方法分类在表1中。

Spatial Decomposition.第一类方法通过空间分解获得等值面，将空间划分为立方体或四面体等单元，并在包含曲面的单元内创建多边形[Bloomenthal 1988;Bloomenthal et al. 1997]。
- 行进立方体(Marching Cubes, MC) [Lorensen and Cline 1987]是这一类中最具代表性的方法。正如最初提出的那样，Marching Cubes遭受拓扑模糊性的困扰，难以表示尖锐的特征。
- 随后的工作改进了为立方体分配多边形类型的查找表[Chernyaev 1995;Hege et al. 1997;Lewiner et al. 2003;Montani et al. 1994;尼尔森2003;Scopigno 1994]或将立方体划分为四面体[Bloomenthal 1994]，并使用类似的Marching tetrahedra [Doi and Koide 1991]来提取等值面。
- 为了更好地捕捉尖锐特征，Dual Contouring (DC) [Ju et al. 2002]将mesh顶点提取到每个单元格的双重表示，并提出根据局部等值面细节估计顶点位置。双轮廓扩展到自适应mesh划分[Azernikov和Fischer 2005]，可以输出四面体mesh。
- 另一种改进的方法是双行进立方体(DMC) [Nielson 2004]，它利用了行进立方体和双轮廓的好处。
- 最近，Neural Marching Cubes [Chen and Zhang 2021]和Neural Dual contourting (NDC) [Chen et al. 2022b]提出了一种数据驱动的方法，将提取的mesh定位为输入域的函数。尽管在已知标量场的提取方面取得了很大进展，但将等曲面方法应用于基于梯度的mesh优化仍然具有挑战性。
Surface Tracking.第二类方法利用曲面跟踪，利用曲面样本之间的相邻信息提取等值面。
- 行进三角形[Hilton et al. 1996,1997]是最早的代表性方法之一，它在Delaunay约束下从初始点迭代地对表面进行三角化。以下工作旨在纳入适应性[Akkouche和Galin 2001;Karkanis and Stewart 2001]或与尖锐特征对齐[McCormick and Fisher 2002]。然而，在曲面跟踪框架中基于梯度的mesh优化需要通过离散的迭代更新过程进行微分，这是一项非常重要的工作。
Shrink Wrapping.第三类的方法依赖于缩小球面mesh[Van Overveld and Wyvill 2004]，或者膨胀临界点[Stander and Hart 1995]来匹配等值面。默认情况下，这些方法仅适用于有限的拓扑情况，并且需要手动选择临界点[Bottino et al. 1996]以支持任意拓扑。此外，通过收缩过程的微分也不是直截了当的，因此这些方法不太适合基于梯度的优化。

Gradient-Based Mesh Optimization in ML

随着机器学习(ML)的最新进展，一些研究探索了用神经网络生成3Dmesh，神经网络的参数通过基于梯度的优化在一些损失函数下进行优化。早期的方法试图预先定义生成形状的拓扑结构，例如球体[Chen等人，2019;Hanocka et al. 2020;Kato et al. 2018;Wang et al. 2018]，原语联合[Paschalidou et al. 2021;Tulsiani et al. 2017]或一组分段部分[Sung et al. 2017;Yin et al. 2020;Zhu et al. 2018]。然而，它们泛化到具有复杂拓扑的对象的能力有限。

为了解决这个问题，AtlasNet [Groueix等人，2018]将3D形状表示为参数表面元素的集合，尽管它不编码连贯表面。Mesh R-CNN [Gkioxari等人，2019]首先预测粗结构，然后细化为表面mesh。这种两阶段方法可以生成具有不同拓扑的mesh，但由于第二阶段仍然依赖于mesh变形，因此无法纠正第一阶段的拓扑误差。
PolyGen [Nash et al. 2020]渐进式生成mesh顶点和边缘，但它们在需要3D地面真实数据方面受到限制。
cvnet [Deng等人，2019]和BSPNet [Chen等人，2020]试图使用形状或二进制平面的凸分解来进行空间划分，但是将它们扩展到mesh上定义的各种目标是非常重要的。

最近，许多研究探索了可微mesh重建方案，该方案从隐函数中提取等值面，通常通过卷积网络或隐神经场进行编码。

Deep Marching Cubes [Liao et al. 2018]计算立方体内可能拓扑的期望，随着grid分辨率的增加，其可扩展性很差。
MeshSDF [Remelli et al. 2020]通过mesh提取提出了一种专门的梯度采样方案，而Mehta et al.[2022]则仔细阐述了神经环境下的水平集进化。
Def Tet [Gao et al. 2020]预测了一个可变形的四面体grid来表示3D对象。
与我们的方法最相似的是DMTet [Shen et al. 2021]，它利用可微的Marching Tetrahedra层来提取mesh。第3节提供了对DMTet的深入分析。

BACKGROUND AND MOTIVATION

在这里，我们首先讨论了常见的现有等面提取方案，以了解它们的缺点并激励我们在第4节中提出的方法。

Problem Statement.
如第1节所述，我们寻求可微mesh优化的表示，其中基本管道是:
i)在空间中定义标量带符号距离函数
ii)将其0-等值面提取为三角形mesh
iii)评估该mesh上的目标函数
iv)将梯度反向传播到底层标量函数。
目前广泛应用于等值面提取的几种流行算法在这种可微环境下仍然存在显著的问题。主要的挑战是，基于梯度的优化的有效性很大程度上取决于等值面提取的特定机制:在基于梯度的优化中使用时，限制性参数化、数值不稳定表达式和拓扑障碍都会导致失败和工件。
我们强调，我们的FlexiCubes表示不是用于从固定的、已知的标量场中提取等值面，这是过去工作中考虑的主要情况。相反，我们特别考虑可微mesh优化，其中底层标量场是未知的，并且在基于梯度的优化过程中执行多次提取。这种设置提供了新的挑战，并激发了专门的方法。

Notation.
我们考虑的所有方法都是从标量函数中提取等值面s: $\mathbb{R}^3\to\mathbb{R},$，在规则grid的顶点采样，并在每个单元内插值。函数s可以直接离散为grid顶点处的值，或者从底层神经网络中评估等，精确参数化s对等值面提取没有影响。为了清楚起见，集合X用单元格C表示grid的顶点，而$M=(V,F)$表示最终提取的mesh与顶点V和面F．我们含蓄地超载了$v\in V{\mathrm{~or~}}x\in X$指一个逻辑顶点，或者指那个顶点在空间中的位置，$x\in\mathbb{R}^3.$。

Marching Cubes & Tetrahedra四面体

最直接的方法是提取grid上有顶点的mesh，每个grid单元内有一个或多个mesh面，如Marching Cubes [Lorensen and Cline 1987]， Marching Tetrahedra [Doi and Koide 1991]，以及许多推广方法。mesh顶点沿着grid边缘提取，其中线性插值的标量函数改变符号
$u_e=\frac{x_a\cdot s(x_b)-x_b\cdot s(x_a)}{s(x_b)-s(x_a)}.$ Eq.1

廖等[2018];Remelli等人[2020]观察到这个表达式包含一个奇点，当$s(v_a)=s(v_b)$，这可能会阻碍微分优化，尽管Shen等人[2021]注意到，在提取过程中，等式1从未在奇异条件下求值。生成的mesh总是无自交(self-intersection-free)和流形(manifold)的
然而，通过构造，通过marching提取得到的mesh顶点只能位于grid边缘的稀疏格上。这样可以防止mesh适合尖锐的特征，并且不可避免地在等面线经过顶点附近时创建质量较差的三角形。最近的方法提出了超越朴素自微分的方案来计算底层标量场的改进梯度[Mehta et al. 2022;Remelli等人2020]，但这并没有解决mesh有限的输出空间。
一种有希望的补救措施是允许底层grid顶点变形[Gao等人，2020;Shen et al. 2021]。虽然这种泛化显著提高了性能，但提取的mesh顶点仍然不能独立移动，导致星形的窄三角形伪像，因为mesh顶点围绕grid上的一个自由度聚集。我们的方法受到Shen等人[2021]的启发，也利用了grid变形，但增加了额外的自由度，以允许顶点的独立重新定位，如图4所示。

Dual Contouring

顾名思义，双重轮廓(Dual Contouring, DC) [Ju et al. 2002]转向双重表示，提取通常可以定位在grid单元内的mesh顶点，以更好地捕捉尖锐的几何特征。每个mesh顶点的位置是通过最小化局部二次误差函数(QEF)来计算的，这取决于标量函数的局部值和空间梯度。
$v_{d}=\underset{v_{d}}{\mathrm{argmin}}\sum_{u_{e}\in\mathcal{Z}_{e}}\nabla s(u_{e})\cdot(v_{d}-u_{e}).$ Eq.2
$u_{e}\in\mathcal{Z}_{e}$是线性插值标量函数沿单元格边缘的过零点。

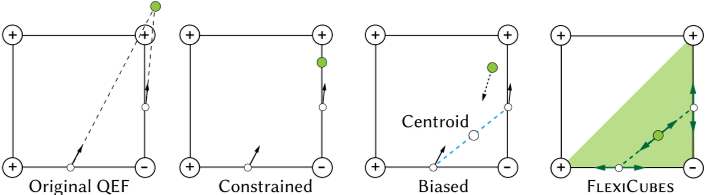
Grad issue in DC左:当求解二次误差函数(QEF)时，结果顶点不能保证在立方体内部。这导致几何和拓扑情况之间的差异。此外，当法线共面时，QEF中存在一个奇异点。虽然已有技术可以通过约束QEF的解空间或使QEF具有正则化损失的偏置来提高直流电的稳定性，但它们在优化设置中不容易适应。前者(第二种)在某些方向上将梯度归零。后者(第三种)很难调整，并且具有很强的正则化将降低DC在灵活性方面的优势。我们的版本(第四版)FlexiCubes提供了额外的自由度，这样对于这个特定的配置，双顶点可以放置在绿色三角形内的任何地方

当从固定的标量函数中提取单个mesh时，双轮廓擅长于拟合尖锐特征，但一些特性阻碍了它在微分优化中的使用。最重要的是，公式2不能保证提取的顶点位于grid单元内。事实上，共面梯度向量$\nabla s(u_{e})$创建退化配置，其中顶点爆炸到一个遥远的位置，导致自相交和数值上不稳定的优化，通过公式进行微分。明确地将顶点限制在单元格中，使梯度归零，并对方程2进行正则化以解决这个问题，从而消除了拟合尖锐特征的能力(图2和图4)。此外，得到的mesh连通性可能是非流形的，输出mesh包含非平面四边形，当它们被分割成三角形时，会引入误差(图3)。

最近关于对双轮廓的推广[Chen et al. 2022b]用学习的神经网络代替了方程2，提高了从不完美但固定的标量函数中提取的质量。然而，当针对底层函数进行优化时，通过额外的神经网络进行区分会进一步使优化环境复杂化，并阻碍收敛(图4)。

我们的方法从这些方法中获得灵感，并且在单元格内自由定位每个顶点的重要性。然而，我们没有明确地将提取的顶点定位为标量场的函数，而是引入了额外的精心选择的自由度，这些自由度被优化为局部调整顶点位置。我们可以通过将我们的方案基于类似但不太为人所知的对偶行进立方体来解决流形问题。

Dual Marching Cubes

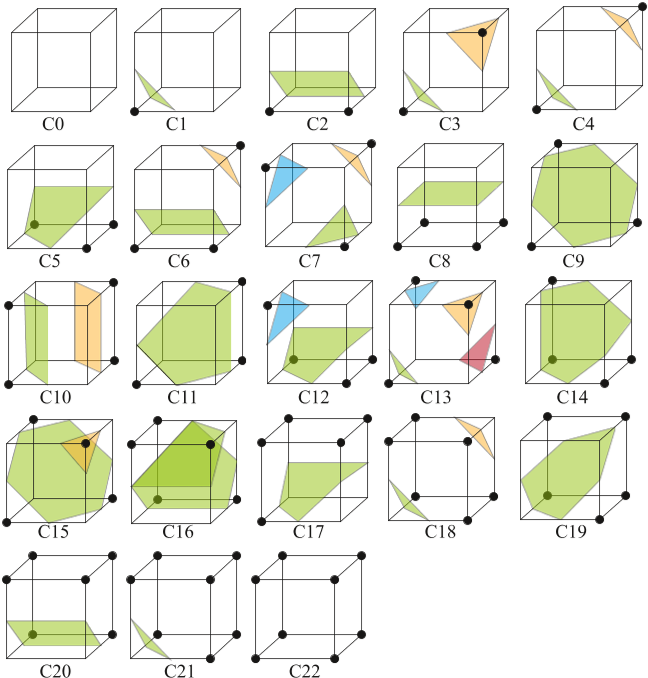
就像双重轮廓一样，双重移动立方体[Nielson 2004]提取grid单元内的顶点。然而，它不是沿着grid的双重连通性提取mesh，而是沿着mesh的双重连通性提取mesh，这些mesh将由Marching Cubes提取。这允许所有配置的流形mesh输出，通过在需要时在单个grid单元内发射多个mesh顶点。提取的顶点位置被定义为类似于双重轮廓的QEF的最小化器[Schaefer等人，2007]，或者作为原始mesh几何的几何函数[Nielson 2004]，如面部质心。

一般来说，与双轮廓相比，双行进立方体提高了提取mesh连通性，但如果使用QEF进行顶点定位，它会受到许多与双轮廓相同的缺点的影响。如果顶点位于原始mesh的质心，则该公式缺乏拟合单个尖锐特征的自由度。在随后的文本中，除非另有说明，否则每当我们提到双行进立方体时，我们指的是质心方法。

我们的方法建立在Dual Marching Cube提取的基础上，但我们引入了额外的参数来定位顶点，从而推广了质心方法。基于一种即使在困难的配置中也能发出正确拓扑的方案是我们成功的关键之一。

METHOD

我们提出了可微mesh优化的FlexiCubes表示。该方法的核心是grid上的标量函数，通过双步立方提取三角形mesh。我们的主要贡献是引入了三组额外的参数，精心选择以增加mesh表示的灵活性，同时保持鲁棒性和易于优化:

Interpolation weights: $\alpha\in\mathbb{R}_{>0}^8,\beta\in\mathbb{R}_{>0}^{12}$ per grid cell, to position dual vertices in space 4.2
Splitting weights: $\gamma\in\mathbb{R}_{>0}$ per grid cell, to control how quadrilaterals四边形 are split into triangles 4.3
Deformation vectors：$\delta\in\mathbb{R}^{3}$ per vertex of the underlying grid for spatial alignment 4.4

这些参数与标量函数一起优化s通过自动分化拟合一个mesh到所需的目标。我们还提出了FlexiCubes表示的扩展，以提取体积的四面体mesh(第4.5节)，并表示具有自适应分辨率的分层meshes(第4.6节)。

Dual Marching Cubes Mesh Extraction

我们首先根据每个grid顶点x标量函数s(x)的值提取Dual Marching Cubes mesh的连通性。正如Nielson [2004];Schaefer等[2007]。The signs of s(x)在立方体角处确定连通性和邻接关系(图7)。与沿着grid边缘提取顶点的普通行军立方体不同，双行军立方体为单元格中的每个原始面提取一个顶点;通常是单个顶点，但也可能多达四个(图7，案例C13)。相邻单元中提取的顶点通过边连接形成双mesh，由四边形面组成(图5)。所得mesh保证是流形的，尽管由于下面描述的额外自由度，它可能很少包含自交;参见7.2节。

AIR