| Title | Geo-Neus: Geometry-Consistent Neural Implicit Surfaces Learning for Multi-view Reconstruction |
|---|---|
| Author | Fu, Qiancheng and Xu, Qingshan and Ong, Yew-Soon and Tao, Wenbi |
| Conf/Jour | NeurIPS |
| Year | 2022 |
| Project | GhiXu/Geo-Neus: Geo-Neus: Geometry-Consistent Neural Implicit Surfaces Learning for Multi-view Reconstruction (NeurIPS 2022) |
| Paper | Geo-Neus: Geometry-Consistent Neural Implicit Surfaces Learning for Multi-view Reconstruction (readpaper.com) Geo-Neus: Geometry-Consistent Neural Implicit Surfaces Learning for Multi-view Reconstruction 基于神经隐式学习的多视图三维重建算法研究 - 中国知网 |
推到了SDF-based Volume Rendering 渲染的颜色监督会造成表面颜色和几何的偏差。(对渲染贡献权重最大的颜色值的位置并不是物体的表面) Bias in color rendering
几何先验:使用COLMAP产生的稀疏点来作为SDF的显示监督—>可以捕获强纹理的复杂几何细节
具有多视图立体约束的隐式曲面上的几何一致监督—>大面积的光滑区域
Conclusion
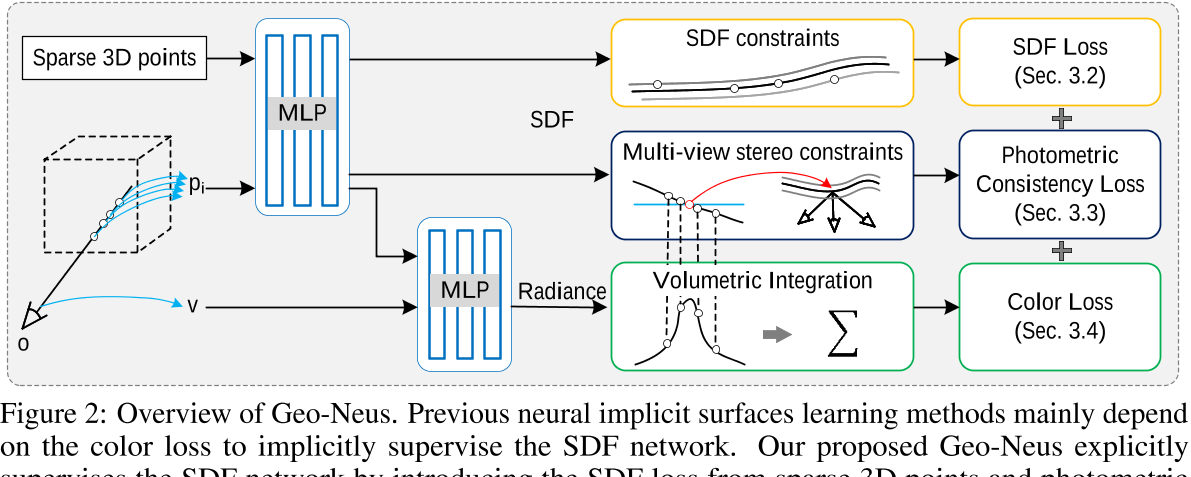
我们提出了 Geo-Neus,这是一种通过执行显式 SDF 优化来执行神经隐式表面学习的新方法。在本文中,我们首先提供了理论分析,即体绘制集成和神经SDF学习之间存在差距。有了这个理论支持,我们建议通过引入两个多视图几何约束来显式优化神经 SDF 学习:来自SFM的稀疏 3D 点和多视图立体中的光度一致性。
通过这种方式,Geo-Neus 在复杂的薄结构和大的光滑区域生成高质量的表面重建。因此,它大大优于最先进的技术,包括传统和神经隐式表面学习方法。我们注意到,虽然我们的方法大大提高了重建质量,但其效率仍然有限。未来,通过快速逐场景辐射场优化方法探索通过体绘制加速神经隐式表面学习将是有趣的。我们没有看到我们工作的直接负面社会影响,但准确的 3D 模型可以从malevolence.中使用。
AIR
近年来,通过体绘制的神经隐式曲面学习成为多视图重建的热门方法。然而,一个关键的挑战仍然存在: 现有的方法缺乏明确的多视图几何约束,因此通常无法生成几何一致的表面重建。为了解决这一挑战,我们提出了几何一致的神经隐式曲面学习用于多视图重建。我们从理论上分析了体绘制积分与基于点的有符号距离函数(SDF)建模之间的差距。为了弥补这一差距,我们直接定位SDF网络的零级集,并通过利用多视图立体中的结构来自运动的稀疏几何(SFM)和光度一致性显式地执行多视图几何优化。这使得我们的SDF优化无偏,并允许多视图几何约束专注于真正的表面优化。大量实验表明,我们提出的方法在复杂薄结构和大面积光滑区域都能实现高质量的表面重建,从而大大优于目前的技术水平。
Introduction
- 传统方法管线:需要深度图或点云来生成表面网格。这些中间表示不可避免地为最终重建的几何引入累积误差。
- 新的方法:从图像中直接重建曲面,有可能减轻累积误差并产生高质量的重建。为了实现这一点,现有的方法将表面表示为神经隐式表示,并利用体积渲染来优化它们。
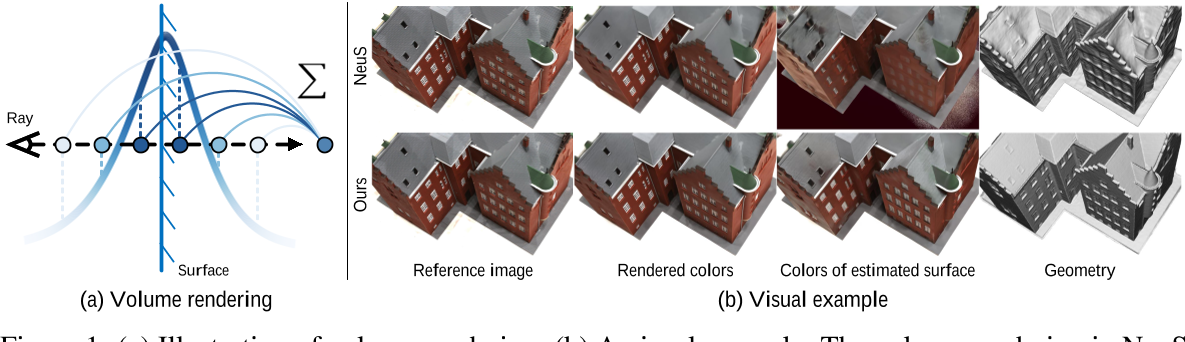
使用rendered的color进行监督,不可避免地会 fail to preserve object geometry information,并且渲染地颜色与估计表面颜色存在着偏差
为了解决上述问题,提出了Geo-Neus,设计一个明确和精确的神经几何优化模型,用于几何一致的神经隐式曲面的体绘制学习,从而实现更好的多视图三维重建。具体而言,我们直接定位SDF网络的零水平集,并通过利用多视图立体中的结构运动稀疏几何(SFM)和光度一致性明确地进行多视图几何优化。
这种模式有几个好处。
- 首先,直接定位SDF网络的零水平集保证了我们的几何建模是无偏的。这使我们的方法能够专注于真正的表面优化。
- 其次,我们证明了在SDF网络的定位零水平集上显式地强制多视图几何约束使我们的方法能够生成几何一致的表面重建。以往的神经隐式曲面学习主要利用渲染损失来隐式优化SDF网络。这导致了训练优化过程中的几何模糊。我们引入的两种类型的明确的多视图约束鼓励我们的SDF网络推理正确的几何形状,包括复杂的薄结构和大的光滑区域。
综上所述,我们的贡献是:
1)我们从理论上分析了体绘制积分和基于点的SDF建模之间存在差距。这表明直接监督SDF网络是促进神经内隐表面学习的必要条件。
2)在理论分析的基础上,提出直接定位SDF网络的零水平集,利用多视图几何约束明确监督SDF网络的训练。通过这种方式,SDF网络被鼓励专注于真正的表面优化。
大量的实验进一步验证了我们的理论分析和提出的SDF网络直接优化的有效性。我们的研究表明,我们提出的Geo-Neus能够重建复杂的薄结构和大的光滑区域。因此,它大大优于目前最先进的表面重建方法,包括传统方法和神经隐式表面学习方法。
Related Work
Traditional multi-view 3D reconstruction
- SFM
- MVS
- Screened Poisson Surface Reconstruction
但由于它们的多个中间步骤没有构成一个整体,在某些情况下存在表面不完备性。
Implicit representation of surface.
根据表面的表示形式,表面重建方法一般可分为显式方法和隐式方法。显式表示包括体素[5,29]和三角网格[3,4,14],它们受到分辨率的限制。隐式表示法使用隐式函数来表示曲面,因此是连续的。可以使用隐式函数在任意分辨率下提取曲面。传统的重建方法,如筛选泊松曲面重建[13],使用基本函数构成隐函数。在基于学习的方法中,最常用的形式是占用函数[20,26]和以网络为代表的有符号距离函数(SDF) [25]
Neural implicit surface reconstruction.
神经隐式场是一种表示物体几何形状的新方法。随着NeRF[21]首次在新颖视图合成中使用多层感知机(Multi-Layer Perceptron, MLP)代表的神经辐射场,大量使用神经网络来表示场景的作品[16,18,30]层出不穷。
- IDR[40]通过将几何表示为被认为是SDF的MLP的零水平集,用神经网络重构曲面。
- MVSDF[41]从MVS网络中导入信息以获得更多的几何先验。
- VolSDF[39]和Neus[33]在渲染过程中使用涉及SDF的权重函数使颜色和几何更接近。
- UNISURF[24]探索了表面绘制和体绘制之间的平衡。
- 与传统的多视图重建方法相比,神经网络重建的曲面具有更好的完备性,特别是在处理非兰伯特情况non-Lambertian cases时。然而,复杂的结构并没有得到很好的处理。同时,平面和尖角也无法保证。
Method
给定目标的多视图图像,我们的目标是在没有mask监督的情况下,通过神经体绘制重建表面。目标的空间场用有符号距离函数(SDF)表示,并利用SDF的零水平集提取相应的表面。在体绘制过程中,我们的目标是优化有符号距离函数。
在本节中,我们首先分析了导致渲染颜色与隐式几何之间不一致的颜色渲染中的固有偏差。然后引入显式SDF优化来实现几何一致性。我们的方法概述如图2所示。

Bias in color rendering
在体渲染的过程中,渲染的颜色与物体的几何形状之间存在间隙。渲染的颜色与表面的真实颜色不一致。
对于不透明实体$\Omega\in\mathbb{R}^3,$其不透明度可以用指标函数$\mathcal{O}(p)$表示:
$\mathcal{O}(\boldsymbol{p})=\left\{\begin{array}{l}1,\boldsymbol{p}\in\Omega\\0,\boldsymbol{p}\notin\Omega\end{array}\right..$ Eq.1
基于不透明固体物体固有的光学特性,我们近似假设图像集$\{I_{i}\}$的颜色C为与对应相机位置o的光线v相交的物体的颜色C:
$C\left(\boldsymbol{o},\boldsymbol{v}\right)=\left.c\left(\boldsymbol{o}+t^*\boldsymbol{v}\right),\right.$ Eq.2
其中$t^*=\operatorname{argmin}\{t|\boldsymbol{o}+t\boldsymbol{v}=\boldsymbol{p},\boldsymbol{p}\in\partial\Omega,t\in(0,\infty)\}.$ ∂Ω表示几何曲面。假设是合适的,因为:
- 透过不透明物体的光可以被忽略。
- 光的强度在穿过不透明物体表面时急剧衰减到零左右。
让我们用带符号的距离函数在数学上表示物体的表面。有符号距离函数sdf (p)是空间点p与曲面∂Ω之间的有符号距离。这样,曲面∂Ω可以表示为:
$\partial\Omega=\left\{\boldsymbol{p}|sdf\left(\boldsymbol{p}\right)=0\right\}.$ Eq.3
通过神经体绘制,我们通过多层感知器(MLP)网络$F_{\Theta}\mathrm{and} G_{\Phi}$估计有符号距离函数$\hat{sdf}$和$\hat{c}$
$\hat{sdf}\left(p\right)=F_{\Theta}\left(p\right),$ Eq.4
$\hat{c}\left(\boldsymbol{o},\boldsymbol{v},t\right)=G_{\Phi}\left(\boldsymbol{o},\boldsymbol{v},t\right).$ Eq.5
因此,相机位置为$\text{o}$的图像的估计颜色可以表示为:$\hat{C}=\int_{0}^{+\infty}w\left(t\right)\hat{c}\left(t\right)dt,$ Eq.6
其中,t是从0点向v方向的射线的深度,$w(t)$是t点的权值。为简单起见,省略了注释o和v。为了得到$w$和$\hat{c}$的离散对应项,我们也沿着射线对$t_{i}$进行离散采样,并使用黎曼和:
$\hat{C}=\sum_{i=1}^nw\left(t_i\right)\hat{c}\left(t_i\right).$ Eq.7
值得注意的是,新视图合成的目标是准确预测颜色$\hat{C},$并努力最小化地面真实图像C与预测图像$\hat{C}$之间的颜色差异:
$C=\hat{C}=\sum_{i=1}^{n}w\left(t_{i}\right)\hat{c}\left(t_{i}\right).$ Eq.8
而在表面重建任务中,我们更关注的是物体的表面而不是颜色。这样,上式可改写为:
- $\hat{sdf}(\hat{t^*})=0,$ 表示估计地表面位置
- $t_{\boldsymbol{j}}$表示离$\hat{t^{*}}$最近的样本点,(表面点可能没有被采样到)
- $\varepsilon_{sample}$表示采样操作引起的偏差,
- $\varepsilon_{weight}$表示体积绘制加权累加操作引起的偏差。(表面点颜色被分到了空气中透明位置)
由式(2)可改写为:
其中,物体表面颜色与估计表面颜色的总偏差为:
相对偏差是:
当$w\left(t_{j}\right)$趋于1时, $\varepsilon_{weight}$趋于0,$\delta c$趋于$\varepsilon_{sample}/c(t^{*})$。在这种情况下,总偏差仅由离散抽样引起,它很小(但仍然存在)。
现有几种神经重构方法的模拟权值如图3所示。可以看出,在实践中几乎不可能做到这一点,特别是在没有任何几何约束的情况下。此外,当处理occlusion的情况时,这个问题变得更加棘手。因此,体绘制积分的加权方式引入了隐式几何建模的bias。由于整个网络的监督几乎完全依赖于渲染颜色和地面真色的差异,这种bias会使表面的颜色和SDF网络难以监督,导致颜色和几何之间的gap。
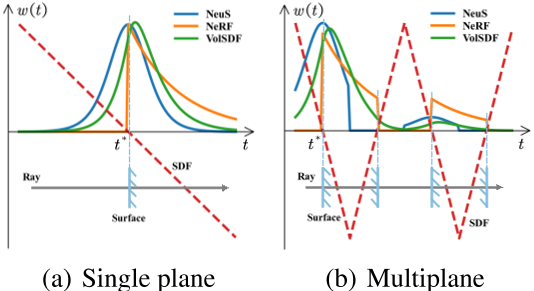
一个简单的解决方案是直接监督对象的几何形状。因此,我们设计了SDF网络上的显式监督和具有多视图约束的几何一致监督。
Explicit supervision on SDF network
SDF网络估计从任意空间点到物体表面的带符号距离,是我们需要优化的关键网络。因此,我们提出了一种对SDF网络进行显式监督的方法,直接利用三维空间中的点来保证其精度。
为了减少额外成本,我们使用由SFM生成的点[27,31]来监督SDF网络。实际上,SFM是一种计算输入图像相机参数的规范解决方案,其中2D特征匹配X和稀疏的3D点P也作为副产品生成。因此,这些稀疏的三维点可以作为“自由的”显式几何信息。近似地,我们假设这些稀疏点在物体表面。即稀疏点的SDF值为零:$sdf\left(\boldsymbol{p}_{i}\right)=0$,其中$\boldsymbol{p}_{i}\in\boldsymbol{P}.$。在实际中,在获得稀疏的3D点后,使用半径滤波器来排除一些离群点[43]。
Occlusion handling
因为我们关注的是不透明的物体,所以物体的某些部分从相机的特定位置来看是不可见的。因此,每个视图中只有一些稀疏点可见。对于相机位置为$o_{i}$的图像$I_{i}$,可见点$P_{i}$与$I_{i}$的特征点$X_{i}$一致:
$X_{i}=K_{i}\left[R_{i}|t_{i}\right]P_{i},$ Eq.14
其中$K_{i}$为内部定标矩阵,$R_i$为旋转矩阵,$t_i$为图像$I_{i}$的平移向量。$X_i\mathrm{~and~}P_i$的坐标都是齐次坐标。为简单起见,省略了$X_{\boldsymbol{i}}$之前的标度指数。根据每张图像的特征点,我们得到每个视图的可见点,并在从对应视图渲染图像时使用它们来监督SDF网络。
View-aware SDF loss.
在从视图$V_{i}$渲染图像$I_i$时,我们使用SDF网络估计可见点$P_{i}\mathrm{~of~}V_{i}$的SDF值。基于稀疏点的SDF值为零的近似,我们提出了视图感知的SDF损失:
$\mathcal{L}_{SDF}=\sum_{p_j\in\boldsymbol{P}_i}\frac{1}{N_i}|\hat{sd}f\left(\boldsymbol{p}_j\right)-sdf\left(\boldsymbol{p}_j\right)|=\sum_{\boldsymbol{p}_j\in\boldsymbol{P}_i}\frac{1}{N_i}|\hat{sd}f\left(\boldsymbol{p}_j\right)|,$ Eq.15
式中,$N_{i}$为$P_{i}$中点的个数,|·|为L1距离。值得注意的是,我们用来监督SDF网络的损失根据所呈现的视图而变化。这样,引入的SDF损耗与显色过程是一致的。
通过对SDF网络的显式监督,我们的网络可以更快地收敛,因为使用了几何先验。此外,由于纹理强烈的复杂几何结构是稀疏点的集中分布区域,因此我们的方法可以捕捉到更细致的几何形状。
Geometry-consistent supervision with multi-view constraints
使用SDF损失,我们的网络可以捕获具有强纹理的复杂几何细节。由于稀疏的3D点主要对纹理丰富的区域提供显式约束,因此大面积的光滑区域仍然缺乏显式的几何约束。为了更进一步,我们设计了具有多视图立体约束的隐式曲面上的几何一致监督
Occlusion-aware implicit surface capture
我们使用曲面的隐式表示,并利用隐式函数的零水平集提取曲面。隐曲面根据式(3),估计曲面为:
$\hat{\partial\Omega}=\left\{\boldsymbol{p}|\hat{sdf}(\boldsymbol{p})=0\right\}.$Eq.16
我们的目标是在不同视图之间使用几何一致的约束来优化$\partial\hat{\Omega}$。因为曲面上的点的数量是无限的,所以在实践中我们需要从$\partial\hat{\Omega}$中采样点。为了与使用视图光线的显色过程保持一致,我们对这些光线上的表面点进行采样。正如3.1中提到的,我们沿着视图射线离散采样,并使用黎曼和来获得渲染的颜色。在采样点的基础上,采用线性插值方法得到曲面点。
在射线上采样点t,对应的三维点为$p=o+tv,$ 预测的SDF值为$\hat{sdf(p)}$,为简单起见,我们进一步将$\hat{sdf(p)}$表示为 $\hat{sdf(t)}$,这是t的函数。我们找到样本点$t_{i}$,其SDF值的符号与下一个样本点$t_{i+1}$不同。由$t_{i}$形成的样本点集T为:
$T=\left\{t_i|\hat{sdf}(t_i)\cdot\hat{sdf}(t_{i+1})<0\right\}.$ Eq.17
在这种情况下,线$t_it_{i+1}$与曲面$\partial\hat{\Omega}.$相交。相交点集合$\hat{T^}$为:
$\hat{T^}=\left\{t|t=\frac{\hat{sd}f(t_i)t_{i+1}-\hat{sd}f(t_{i+1})t_i}{\hat{sd}f(t_i)-\hat{sd}f(t_{i+1})},t_i\in T\right\}.$ Eq.18
与物体相互作用的光线可能与物体表面有不止一个交点。具体来说,可能至少有两个交叉点。与SDF监督机制类似,考虑到遮挡问题,我们只使用沿光线的第一个交点
$t^=\operatorname{argmin}\left\{t|t\in\hat{T^}\right\}.$ Eq.19
$t^*$的选择保证隐式曲面的样本点在对应的视图中都是可见的,并且使监督与显色过程一致。
Multi-view photometric consistency constraints
我们捕获估计的隐式曲面,其几何结构在不同的视图中应该是一致的。基于这种直觉,我们使用多视图立体(MVS)中的光度一致性约束[8,9,34]来监督我们提取的隐式表面。
对于表面上的一个小面积s, s在图像上的投影是一个小的像素斑q。除了遮挡情况外,s对应的斑在不同视图之间应该是几何一致的。与传统MVS方法中的补片变形类似,我们用中心点及其法线表示s。为方便起见,我们在参考图像$I_{r}$的相机坐标中表示s的平面方程:
$n^Tp+d=0,$ Eq.20
式中,p为式(19)计算得到的交点,$n^{T}$为SDF网络在p点自动微分计算得到的法线,则参考图像$I_{r}$的像素patch $q_{i}$中的图像点x与源图像$I_{s}$的像素patch $q_{i}$中的对应点x′通过平面诱导的单应性H相关联[11]
$x=Hx^{\prime},H=K_s(R_sR_r^T-\frac{R_s(R_s^Tt_s-R_r^Tt_r)n^T}{d})K_r^{-1},$ Eq.21
其中K为内部校准矩阵,R为旋转矩阵,t为平移向量。索引显示捐赠属于哪个图像。为了集中几何信息,我们将彩色图像$\left\{I_{i}\right\}$转换为灰度图像$\left\{I’_{i}\right\}$,并利用$\left\{I’_{i}\right\}$中斑块间的光度一致性来监督隐式表面。
Photometric consistency loss.
为了测量光度一致性,我们使用参考灰度图像$\left\{I’_{r}\right\}$和源灰度图像$\left\{I’_{s}\right\}$中斑块patches的归一化互相关(NCC):
$NCC(I_{r}’(q_{i}),I_{s}’(q_{is}))=\frac{Cov(I_{r}’(q_{i}),I_{s}’(q_{is}))}{\sqrt{Var(I_{r}’(q_{i}))Var(I_{s}’(q_{is}))}},$ Eq.22
其中Cov表示协方差,var表示方差。在对图像进行颜色渲染时,我们使用以被渲染像素为中心的patch, patch的大小为11 × 11。我们将渲染图像作为参考图像,并计算其采样补丁与所有源图像上相应补丁之间的NCC分数。为了处理遮挡,我们为每个采样patch找到计算出的NCC分数中最好的四个[9],并使用它们来计算相应视图的光度一致性损失:
$\mathcal{L}_{photo}=\frac{\sum_{i=1}^{N}\sum_{s=1}^{4}1-NCC(I_{r}^{\prime}(q_{i}),I_{s}^{\prime}(q_{is}))}{4N},$ Eq.23
其中N是渲染图像上采样像素的数量。在光度一致性损失的情况下,保证了隐式曲面在多视图间的几何一致性。
Loss function
在渲染特定视图的颜色时,我们的总损失是:
$\mathcal{L}=\mathcal{L}_{color}+\alpha\mathcal{L}_{reg}+\beta\mathcal{L}_{SDF}+\gamma\mathcal{L}_{photo}.$ Eq.24
$\mathcal{L}_{color}=\frac1N\sum_{i=1}^N|C_i-\hat{C}_i|.$
$\mathcal{L}_{reg}=\frac1N\sum_{i=1}^{N}(|\nabla\hat{sd}f(\boldsymbol{p}_{i})|-1)^{2}.$ eikonal项用来正则化SDF网络的梯度
在我们的实验中,我们选择α, β和γ分别为0.3,1.0和0.5。
Experiments
Datasets
- DTU
- BlendedMVS
Baselines
- COLMAP
- IDR
- VolSDF
- NeuS
- NeuralWarp
Implementation details.
- MLP SDF : 256x8
- MLP color:256x4
- PE:L=6—>x , L=4—>dirs
- bathsize rays = 512
- 单个2080Ti 16h
- 提取mesh resolution = $512^{3}$
Comparisons
- quantitative results
- Qualitative results
Analysis
- Ablation study
- Geometry bias of volumetric integration.
- Convergence speed.