| Title | HF-NeuS: Improved Surface Reconstruction Using High-Frequency Details |
|---|---|
| Author | _Yiqun Wang, Ivan Skorokhodov, Peter Wonka_ |
| Conf/Jour | NeurIPS |
| Year | 2022 |
| Project | yiqun-wang/HFS: HF-NeuS: Improved Surface Reconstruction Using High-Frequency Details (NeurIPS 2022) (github.com) |
| Paper | Improved surface reconstruction using high-frequency details (readpaper.com) |
贡献:
- 新的SDF与透明度$\alpha$关系函数,相较于NeuS更简单
- 将SDF分解为两个独立隐函数的组合:基和位移。并利用自适应尺度约束对隐函数分布不理想的区域进行重点优化,可以重构出比以往工作更精细的曲面
Limitation
如图5所示,我们的方法仍然存在挑战。我们给出了参考地面真值图像、相应的重建图像和重建表面。对于船舶的绳索网格,仍然观察到对地面真实辐射的一些过拟合。具体来说,绳子的网格在图像中是可见的,但表面没有精确地重建。另一个限制是缺少单根细绳。我们还可视化了表1的一个坏情况,其中误差大于其他方法的误差,如补充材料中的图14 DTU Bunny所示。在这种情况下,这个模型的光线变化,纹理不那么明显,因此很难重建腹部的细节。

Conclusion
介绍了一种基于高频细节的多视点表面重建新方法HF-NeuS。我们提出了一个新的推导来解释符号距离和透明度之间的关系,并提出了一类可以使用的函数。通过将符号距离场分解为两个独立隐函数的组合,并利用自适应尺度约束对隐函数分布不理想的区域进行重点优化,可以重构出比以往工作更精细的曲面。
实验结果表明,该方法在定量重建质量和视觉检测方面都优于目前的技术水平。目前的一个限制是,HF-NeuS需要优化一个额外的隐式函数,因此它需要更多的计算资源,并产生额外的编码复杂性。此外,由于缺乏3D监督,我们仍然在一定程度上观察到对地面真实度的过拟合。
未来工作的一个有趣的方向是探索不同照明方式下场景的重建。最后,我们不期望与我们的研究直接相关的负面社会影响。不过,一般来说,地表重建可能产生负面的社会影响
AIR
神经渲染可以在没有三维监督的情况下重建形状的隐式表示。然而,目前的神经表面重建方法难以学习高频几何细节,因此重建的形状往往过于光滑。本文提出了一种提高神经绘制中表面重建质量的新方法HF-NeuS。我们遵循最近的工作,将曲面建模为有符号距离函数(sdf)。
首先,我们推导了SDF、体积密度、透明度函数和体积渲染方程中使用的加权函数之间的关系,并提出了将透明度建模为转换后的SDF。
其次,我们观察到,试图在单个SDF中联合编码高频和低频分量会导致不稳定的优化。
我们提出将SDF分解为基函数和位移函数,采用由粗到精的策略,逐步增加高频细节。最后,我们设计了一种自适应优化策略,使训练过程专注于改进那些靠近表面的sdf有伪像的区域。我们的定性和定量结果表明,我们的方法可以重建细粒度的表面细节,并获得比现有技术更好的表面重建质量
NeRF —> Neus、VolSDF表面重建 —> HF-Neus
- 首先,我们分析了符号距离函数与体积密度、透明度和权重函数之间的关系。我们从我们的推导中得出结论,最好是建模一个将有符号距离映射到透明度的函数,并提出一类满足理论要求的函数
- 其次,我们观察到,如图2所示,单符号距离函数很难直接学习高频细节。因此,我们建议在相关工作之后将SDF分解为基函数和位移函数。我们将这一思想应用于可微分的NeRF渲染框架和NeRF训练方案。
- 第三,可以选择将距离转换为透明度的函数有一个参数,我们称之为尺度s,它控制函数的斜率(或导数的偏差)。参数s控制表面被定位的精确程度,以及远离表面的颜色对结果的影响程度。
- 在之前的工作中,这个参数s是全局设置的,但它是可训练的,因此它可以在迭代之间改变。我们提出了一种新的空间自适应加权方案来影响该参数,使优化更加关注距离场中的问题区域

RW:
- Multi-view 3D reconstruction.
- Neural implicit surfaces.
- DVR、IDR、NeRF++、UNISURF、VolSDF、Neus、NeuralPatch
- High-frequency detail reconstruction.
- SIREN、MipNeRF、
Method
输入N张图片$I=\{I_1,I_2…I_N\}$及对应相机内外参$\Pi=\{\pi_1,\pi_2…\pi_N\}.$
1)首先,我们展示了如何将带符号的距离函数嵌入到体绘制的公式中,并讨论了如何建模距离和透明度之间的关系。
2)然后,我们提出利用额外的位移符号距离函数将高频细节添加到基本符号距离函数中。
3)最后,我们观察到将带符号距离映射到透明度的函数由一个参数s控制,该参数s决定了函数的斜率。我们提出了一种方案,根据距离场的梯度范数以空间变化的方式设置该参数s,而不是在单个训练迭代中对整个体积保持恒定。
Modeling transparency as transformed SDF
NeRF
光线$\mathbf{r}(t)=\mathbf{o}+\mathbf{t}\mathbf{d},$
对应像素的颜色$C(\mathbf{r})=\int_{t_n}^{t_f}T(t)\sigma(\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t),\mathbf{d})dt$
透明度$T(t)=\exp\left(-\int_{t_{n}}^{t}\sigma(\mathbf{r}(s))ds\right),$是一个单调递减函数
为了将SDF转换为密度,需要找到一个函数
- VolSDF中提出的密度函数:$\sigma(\mathbf{r}(t))=\Psi\left(f\left(\mathbf{r}(t)\right)\right)$
- Neus中提出的权重函数:$w((t))=\Psi\left(f\left(\mathbf{r}(t)\right)\right)$
- 本文给出了密度函数σ表达式的一个复杂推导
- $T(t)=\Psi\left(f\left(\mathbf{r}(t)\right)\right),$
- $\sigma(\mathbf{r}(t_{i}))=s\left(\Psi\left(f\left(\mathbf{r}(t_{i})\right)\right)-1\right)\nabla f\left(\mathbf{r}(t_{i})\right)\cdot\mathbf{d}$
- $\alpha_i=1-exp\left(-\sigma_i\left(t_{i+1}-t_i\right)\right)$,并将$\alpha$clamp在0,1之间
与NeuS相比,我们得到了更简单的密度σ的离散化计算公式,减少了NeuS中除法带来的数值问题。此外,我们的方法不需要涉及两个不同的采样点,即截面点和中点,这使得它更容易满足无偏加权函数。由于不需要为两个不同的点集分别计算SDF和颜色,因此与NeuS相比,颜色和几何形状更加一致。与VolSDF[32]相比,由于透明度函数是显式的,因此我们的方法可以使用逆CDF计算的逆分布抽样来满足近似质量。因此不需要像VolSDF那样复杂的采样方案。图3显示了一个直观的比较。
Implicit displacement field without 3D supervision
为了实现多尺度拟合框架,我们建议将SDF建模为基距离函数和沿基距离函数法线的位移函数的组合。隐式位移函数是一个附加的隐式函数。这样设计的原因是单个隐式函数很难同时学习低频和高频信息。隐式位移函数可以补充基本隐式函数,从而更容易学习高频信息。
与从点云中学习隐式函数的任务相比,从多幅图像中重建三维形状使得高频内容的学习更加困难。我们建议使用神经网络在多个尺度上学习频率,并以由粗到细的方式逐步增加频率内容。
基面的隐式函数$f_{b}$
位移隐式函数$f_{d’}$:将基面上点$x_{b}$沿着法向$n_{b}$,映射到表面点x
$f_d$将基面上点x沿着法向$n_{b}$映射到表面点$x_{b}$,因此$\mathop{:}f_{d^{\prime}}(\mathbf{x}_{b})=f_{d}(\mathbf{x}).$
由于隐函数的性质,这两个函数之间的关系可以表示为:$f_b(\mathbf{x}_b)=f(\mathbf{x}_b+f_{d^{\prime}}\left(\mathbf{x}_b\right)\mathbf{n}_b)=0$
$\mathbf{n}_b=\frac{\nabla f_b(\mathbf{x}_b)}{|\nabla f_b(\mathbf{x}_b)|},$ 是$x_{b}$在基面上的法线。为了计算隐函数f的表达式,引入$\mathbf{x}_b=\mathbf{x}-f_{d^{\prime}}\left(\mathbf{x}_b\right)\mathbf{n}_b$并得到组合隐函数的表达式:$f(\mathbf{x})=f_b(\mathbf{x}-f_d\left(\mathbf{x}\right)\mathbf{n}_b)$
因此,我们可以用基隐函数和位移隐函数来表示组合隐函数。
然而,出现了两个挑战
- 首先,只有当点x在表面上时,才满足式10。
- 其次,当只知道位置x时,很难估计点$x_{b}$处的法线。
我们依靠两个假设来解决问题
- 一个假设是,这种变形可以应用于所有等面,即$f_b(\mathbf{x}_b)=f(\mathbf{x}_b+f_{d^{\prime}}\left(\mathbf{x}_b\right)\mathbf{n}_b)\stackrel{\cdot}{=}c.$。这样,假设方程对体积中的所有点都有效,而不仅仅是在表面上。
- 另一假设是$x_{b}$和x距离不太远,则可以将式(10)中x点上的$\mathbf{n}_b$替换为法向$\mathbf{n}$。我们使用位移约束$4\Psi_{s}^{\prime}(f_{b})$来控制隐式位移函数的大小。
$f(\mathbf{x})=f_b(\mathbf{x}-4\Psi_{(0.01s)}^{\prime}(f_b)f_d\left(\mathbf{x}\right)\mathbf{n})$
为了精确控制频率,我们采用位置编码对基隐函数和位移隐函数分别进行编码。频率可以通过一种从粗到精的策略来明确控制,而不是简单地使用两个具有两个不同频率级别的Siren网络
$\gamma(\mathbf{x})=[\gamma_0(\mathbf{x}),\gamma_1(\mathbf{x}),…,\gamma_{L-1}(\mathbf{x})]$
每个分量由不同频率的sin和cos函数组成$\gamma_j(\mathbf{x})=\left[\sin\left(2^j\pi\mathbf{x}\right),\cos\left(2^j\pi\mathbf{x}\right)\right]$
直接学习高频位置编码会使网络容易受到噪声的影响,因为错误学习的高频会阻碍低频的学习。如果有三维监控,这个问题就不那么明显了,但是图像的高频信息很容易以噪声的形式引入到表面生成中。我们使用Park等人Nerfies[24]提出的从粗到精的策略,逐步增加位置编码的频率。
$\gamma_{j}(\mathbf{x},\mathbf{\alpha})=\omega_{j}\left(\mathbf{\alpha}\right)\gamma_{j}(\mathbf{x})=\frac{\left(1-\cos\left(clamp\left(\alpha L-j,0,1\right)\pi\right)\right)}2\gamma_{j}(\mathbf{x})$
$\alpha\in[0,1]$是控制所涉及频率信息的参数。在每次迭代中,α增加$1/n_{max}$,直到它接近1,其中$n_{max}$是最大迭代次数。
我们利用两种不同参数$\alpha_b.$和$\alpha_d.$的位置编码$\gamma(\mathbf{x},\alpha_b),\gamma(\mathbf{x},\alpha_d)$。为简单起见,我们设$\alpha_{b}=0.5\alpha_{d}$,只控制$\alpha_d$。我们还使用了两个MLP函数$MLP_{b},MLP_{d}$来拟合基函数和位移函数。
$f(\mathbf{x})=MLP_{b}(\gamma(\mathbf{x},\alpha_{b})-4\Psi_{s}^{\prime}(f_{b})MLP_{d}\left(\gamma(\mathbf{x},\alpha_{d})\right)\mathbf{n}),$
$\begin{array}{rcl}\mathbf{n}&=&\frac{\nabla f_b(\mathbf{x})}{|\nabla f_b(\mathbf{x})|}\end{array}$ 可以通过MLP b的梯度来计算
$\Psi_s^{\prime}(f_b)\quad=\Psi_s^{\prime}(MLP_b(\gamma(\mathbf{x},\alpha_b))).$
训练时应clamp位移约束的s。
我们将这个隐式函数带入Eq.(6)来计算透明度,这样图像的亮度(颜色)$\hat{C}_{s}$就可以通过体积渲染方程来计算。
为了训练网络,我们使用了损失函数$\mathcal{L}=\mathcal{L}_{rad}+\mathcal{L}_{reg}.$,它包含了带符号距离函数的辐射损失和Eikonal正则化损失。对于正则化损失,我们同时约束了基本隐函数和详细隐函数。$\mathcal{L}=\frac{1}{M}\sum_{s}\left|\hat{C}_{s}-C_{s}\right|_{1}+\frac{1}{N}\sum_{k}\left[\left(|\nabla f_{b}(\mathbf{x}_{k})|_{2}-1\right)^{2}+\left(|\nabla f(\mathbf{x}_{k})|_{2}-1\right)^{2}\right]$
Modeling an adaptivate transparency function
在前面的小节中,透明度函数被定义为sigmoid函数,由一个标度s控制。该参数控制着sigmoid函数的斜率,同时也是导数的标准差。我们也可以说它控制着函数的平滑度。当s较大时,随着位置远离表面,s型函数的值急剧下降。相反,当s较小时,该值平稳减小。然而,每次迭代选择单个参数会在体块的所有空间位置产生相同的行为。
由于需要重构两个带符号的距离函数,特别是在高频叠加之后,很容易出现Eikonal方程不满足的情况,即SDF的梯度范数在某些位置不为1。即使有正则化损失,也不可能避免这个问题。
我们建议使用带符号距离场的梯度范数以空间变化的方式对参数s进行加权。当沿射线方向的梯度范数大于1时,我们增加s。这意味着当梯度的范数大于1时,隐函数的变化更剧烈,这表明了一个需要改进的区域。在某些区域使距离函数更大,需要更精确的距离函数,并且由于不正确的距离函数而放大误差,特别是在表面附近。为了自适应地修改量表s,我们提出如下公式:
$T(t)=\left(1+e^{-s\exp\left(\sum_{i=1}^{K}\omega_i|\nabla f_i|-1\right)f(\mathbf{r}(t))}\right)^{-1},$
其中∇f为带符号距离函数的梯度,K为采样点个数
$ω_i$ 为归一化后的$\Psi_s^{\prime}(f_i)$作为权值,$\sum_{i=1}^{K}\omega_{i}=1.$
该方法既可用于控制透明度函数,也可用于标准NeRF提出的分层采样阶段。通过局部增大s,在距离值变化较快的表面附近会产生更多的样本。这种机制也有助于优化集中在这些区域的体积。
Experiments
Baselines:Neus、VolSDF、NeRF
Datasets:DTU、BlendedMVS
Evaluation metrics:CD(chamfer distance)、PSNR
Implementation details:
- GPU A100 40GB
- lr = 5e-4
- 首先64个均匀采样点,计算点的SDF和梯度,然后计算s参数增益,根据增益自适应更新权重
- 然后根据权重额外采样64个点
- 当$\alpha^{0}_{d}=0$时产生光滑的结果,本文使用$\alpha^{0}_{d}=0.5$ ,$\alpha^{0}_{b}=0.5 \alpha^{0}_{d}=0.25$
- 位置编码L=16
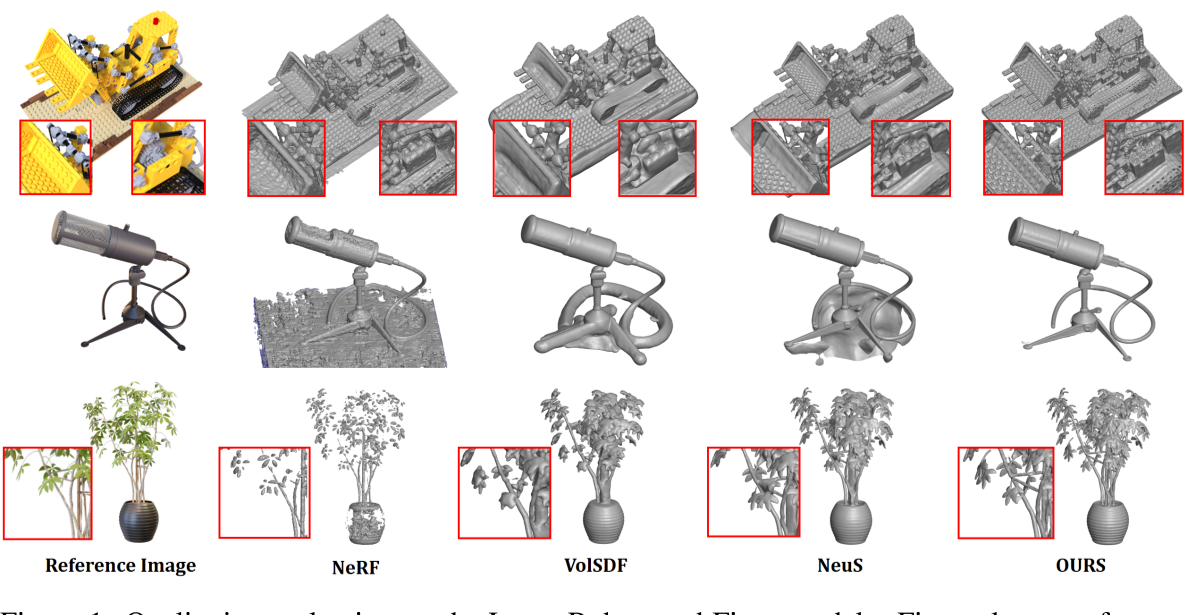
Comparison:
- 定性+定量
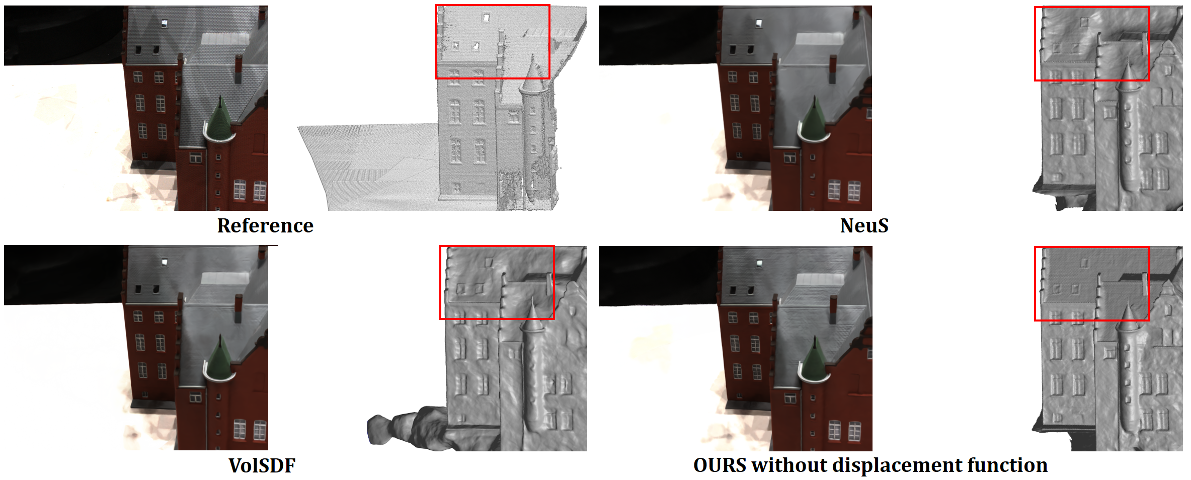
Ablation study.
- Coarse2Fine module
- Implicit displacement function module
- Position-adaptive s module