| Title | Multiview Neural Surface Reconstruction by Disentangling Geometry and Appearance |
|---|---|
| Author | Lior Yariv, Yoni Kasten, Dror Moran, Meirav Galun, Matan Atzmon, Ronen Basri, Yaron Lipman |
| Conf/Jour | NeurIPS |
| Year | 2020 |
| Project | Multiview Neural Surface Reconstruction by Disentangling Geometry and Appearance (lioryariv.github.io) |
| Paper | Multiview Neural Surface Reconstruction by Disentangling Geometry and Appearance (readpaper.com) |
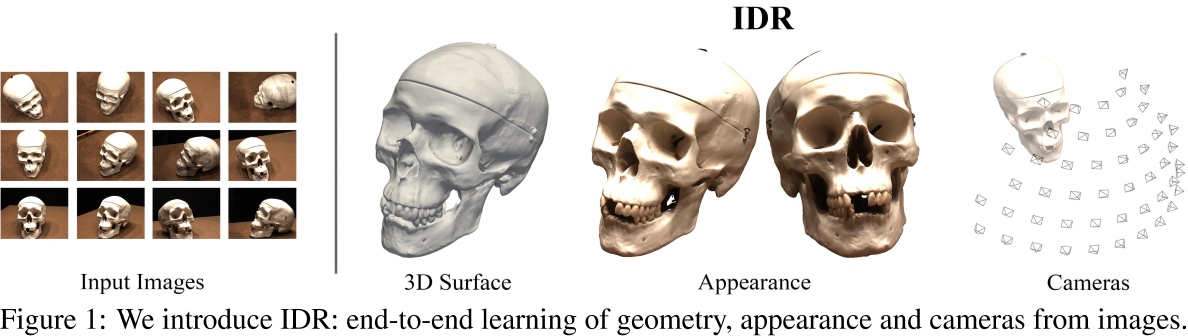
端到端的IDR:可以从masked的2D图像中学习3D几何、外观,允许粗略的相机估计
Conclusion
我们介绍了隐式可微分渲染器(IDR),这是一个端到端的神经系统,可以从masked 2D图像和噪声相机初始化中学习3D几何、外观和相机。仅考虑粗略的相机估计允许在现实场景中,准确的相机信息不可用稳健的3D重建。
我们的方法的一个限制是,它需要一个合理的相机初始化,不能工作在随机相机初始化。
未来有趣的工作是
- 将IDR与直接从图像中预测相机信息的神经网络结合起来。
- 另一个有趣的未来工作是进一步将表面光场(公式5中的M0)分解为材料(BRDF, B)和场景中的光(Li)。
最后,我们希望将IDR整合到其他计算机视觉和学习应用中,例如3D模型生成,以及从野外图像中学习3D模型。
AIR
在这项工作中,我们解决了多视图三维表面重建的挑战性问题。我们引入了一个神经网络架构,它可以同时学习未知的几何形状、相机参数和一个神经渲染器,它可以近似地从表面反射到相机的光。几何图形表示为神经网络的零水平集,而从渲染方程导出的神经渲染器能够(隐式地)对各种照明条件和材料进行建模。我们在来自DTU MVS数据集的具有不同材质属性、光照条件和噪点相机初始化的物体的真实世界2D图像上训练我们的网络。我们发现我们的模型可以产生高保真度、分辨率和细节的最先进的3D表面重建。
Introduction
NeRF:基于NN的方法可以从2D图像中学习3D形状
- Differential rendering: 基于ray casting/tracing或rasterization光栅化
- 3D geometry represent : pointcloud , triangle meshes , implicit representations defined over volumetric grids, neural implicit representations
neural implicit representations主要优点是它们在表示任意形状和拓扑的表面方面的灵活性,以及无网格性(即,没有固定的先验离散化,如体积网格或三角形网格)。but: 到目前为止,具有隐式神经表征的可微渲染系统[30,31,40]并没有纳入在图像中产生faithful3D几何外观所需的照明和反射特性,也没有处理可训练的摄像机位置和方向。
目标是设计一个end-to-end neural architecture system该系统可以从masked的2D图像和粗略的相机估计中学习3D几何形状,并且不需要额外的监督。为了实现这一目标,我们将像素的颜色表示为场景中三个未知数的可微分函数:几何、外观和相机。在这里,外观是指定义表面光场的所有因素的总和,不包括几何形状,即表面双向反射分布函数(BRDF)和场景的照明条件。我们称这种架构为隐式可微分渲染器(IDR)。我们表明,IDR能够近似从3D形状反射的光,3D形状表示为神经网络的零水平集。该方法可以处理某一限定族的表面外观,即所有表面光场都可以表示为表面上的点、其法线和观测方向的连续函数。此外,将全局形状特征向量合并到IDR中可以增加其处理更复杂外观(例如,间接照明效果)的能力。
与我们的论文最相关的是DVR[40],该论文首先引入了隐式神经占用函数的完全可微渲染器Occupy Network[37],这是上文定义的隐式神经表示的一个特定实例。虽然他们的模型可以表示任意的颜色和纹理,但它不能处理一般的外观模型,也不能处理未知的、有噪声的相机位置。例如,我们表明[40]中的模型以及其他几个基线无法生成Phong反射模型[8]。此外,我们通过实验证明,IDR可以从2D图像以及精确的相机参数中产生更精确的3D形状重建。值得注意的是,虽然基线在高光场景中经常产生形状伪影,但IDR对这种照明效果具有鲁棒性。我们的代码和数据可在https://github.com/lioryariv/idr上获得。
贡献:
- 端到端架构,处理未知的几何形状、外观和相机。
- 表达神经隐式曲面对摄像机参数的依赖关系。
- 从现实生活中的2D图像,通过精确和noise的相机信息,产生具有广泛外观的不同物体的最先进的3D表面重建。
Previous work
用于学习几何的可微渲染系统(主要)有两种风格:可微光栅化[32,23,10,29,4]和可微光线投射。由于目前的工作属于第二类,我们首先集中讨论这一类工作。然后介绍了多视图曲面重建和神经视图合成的相关工作。
Implicit surface differentiable ray casting
可微光线投射主要用于隐式形状表示,如在体积网格上定义的隐式函数或隐式神经表示,其中隐式函数可以是占位函数[37,5],有符号距离函数(SDF)[42]或任何其他有符号隐式[2]。
- 在一项相关工作中,[20]SDFDiff使用体积网格来表示SDF并实现光线投射可微分渲染器。它们近似于每个体积单元中的SDF值和表面法线。
- [31]DIST使用预训练的DeepSDF模型[42]的球体跟踪,并通过区分球体跟踪算法的各个步骤来近似深度梯度与DeepSDF网络的潜在代码;
- [30]使用现场探测来促进可微射线投射。与这些作品相比,IDR利用了精确可微的曲面点和隐曲面的法线,并考虑了更一般的外观模型,并处理了噪声相机。
Multi-view surface reconstruction
在图像的捕获过程中,深度信息会丢失。假设已知摄像机,经典的多视点立体(Multi-View Stereo, MVS)方法[9,48,3,54]试图通过匹配视图间的特征点来重现深度信息。然而,要产生有效的三维水密表面重建,需要深度融合[6,36]的后处理步骤,然后是泊松表面重建算法[24]。
- 最近的方法使用场景集合来训练深度神经模型,用于MVS管道的子任务,例如特征匹配[27]或深度融合[7,44],或用于端到端MVS管道[16,56,57]。当相机参数不可用时,给定一组来自特定场景的图像,应用运动结构(SFM)方法[51,47,22,19]来重现相机并进行稀疏的3D重建。
- Tang和Tan[53]BA-Net使用具有集成可微束调整[55]层的深度神经结构提取参考帧深度的线性基础,并从附近图像中提取特征,并优化每个前向通道的深度和相机参数。与这些工作相反,IDR使用来自单个目标场景的图像进行训练,从而产生精确的水密3D表面重建。
Neural representation for view synthesis.
最近的工作训练神经网络从已知相机的有限图像集预测 3D 场景或对象的新视图和一些几何表示。
- [50]SRN使用 LSTM 对场景几何进行编码以模拟光线行进过程。
- [38]NeRF使用神经网络来预测体积密度和视相关的发射辐射,从一组具有已知相机的图像中合成新的视图。
- [41]Learning Implicit Surface Light Fields使用神经网络从输入图像和几何中学习表面光场,并预测未知视图和/或场景照明。与IDR不同的是,这些方法不会产生场景几何的三维表面重建,也不处理未知的相机
Method
我们的目标是从具有可能粗糙或嘈杂的相机信息的masked 2D 图像中重建物体的几何形状。有三个未知数:
(i)几何,由参数$\theta\in\mathbb{R}^m$表示;
(ii)外观,用$\gamma\in\mathbb{R}^n$表示;
(iii)由$\tau\in\mathbb{R}^k.$表示的摄像机。符号和设置如图 2 所示。
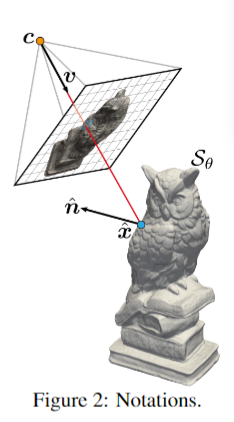
我们将几何图形表示为神经网络 (MLP) f 的零水平集,$\mathcal{S}_\theta=\left\{x\in\mathbb{R}^3\mid f(\mathbf{x};\theta)=0\right\},$ Eq.1
可学习参数$\theta\in\mathbb{R}^m$。为了避免任何地方 0 解,f 通常进行正则化 [37, 5]。我们选择 f 将符号距离函数 (SDF) 建模为其零水平集 $s_{\theta}$[42]。我们使用隐式几何正则化 (IGR) [11] 强制执行 SDF 约束,稍后详细介绍。
SDF在我们的上下文中有两个好处:首先,它允许使用球体跟踪算法进行有效的光线投射[12,20];其次,IGR具有有利于光滑和逼真的表面的隐式正则化。
IDR forward model.
给定一个由 p 索引的像素,与某个输入图像相关联,让 $R_p(\tau)=\{c_p+t\mathbf{v}_p\mid t\geq0\}$ 通过像素 p 表示射线,其中 $c_p=c_p(\tau)$ 表示相应相机的未知中心,$\mathbf{v}_p=\mathbf{v}_p(\tau)$ 射线的方向(即从$c_{p}$指向像素p的向量)。令$\hat{\mathbf{x}}_{p}=\hat{\mathbf{x}}_{p}(\mathbf{\theta},\tau)$表示射线 $R_{p}$ 和表面$\mathcal{S}_{\theta}$ 的第一个交集。沿$R_{p}$的传入射线,它确定像素 $L_{p}=L_{p}(\theta,\gamma,\tau)$的呈现颜色,是$\hat{x}_{p}$处表面属性的函数,$\hat{x}_{p}$处的传入辐射,以及观看方向 $v_{p}$。反过来,我们假设表面属性和传入的辐射是表面点$\hat{x}_{p}$的函数,及其对应的表面正态$\hat{\mathbf{n}}_{p}=\hat{\mathbf{n}}_{p}(\theta),$查看方向$v_{p}$和全局几何特征向量$\hat{\mathbf{z}}_p=\hat{\mathbf{z}}_p(\hat{\mathbf{x}}_p;\theta)$。因此,IDR 前向模型是:
$L_p(\theta,\gamma,\tau)=M(\hat{x}_p,\hat{n}_p,\hat{z}_p,v_p;\gamma),$ Eq.2
其中 M 是第二个神经网络 (MLP)。我们在比较 $L_{p}$和像素输入颜色$I_{p}$的损失中使用 $L_{p}$ 来同时训练模型的参数 $\theta,\gamma,\tau.$。接下来,我们提供有关等式 2 中模型不同组件的更多详细信息。
Differentiable intersection of viewing direction and geometry
此后(直到第 3.4 节),我们假设一个固定的像素 p,并删除下标 p 符号以简化符号。第一步是将交点 $\hat{\mathbf{x}}(\theta,\tau):$表示为参数为 θ, τ 的神经网络。这可以通过对几何网络 f 稍作修改来完成。
令$\hat{\mathbf{x}}(\theta,\tau)=c+t(\theta,c,v)\mathbf{v}$表示交点。由于我们的目标是在类似梯度下降的算法中使用 $\hat{x}$,我们需要确保我们的推导在当前参数的值和一阶导数中是正确的,用 $\theta_0,\tau_0$表示;因此,我们将$c_{0}=c(\tau_{0}),$ $v_0=v(\tau_0),$ $t_0=t(\theta_0,c_0,v_0),$ $\mathrm{and~}$ $x_0=\hat{x}(\theta_0,\tau_0)=c_0+t_0v_0.$
设$S_{\theta}$定义为式1。射线$R(\tau)$与表面$\mathcal{S}_{\theta}$的交点可以用公式表示
$\hat{x}(\theta,\tau)=c+t_0\mathbf{v}-\frac v{\nabla_xf(x_0;\theta_0)\cdot v_0}f(\mathbf{c}+t_0\mathbf{v};\theta),$ Eq.3
在$\theta=\theta_{0}.$和$\tau=\tau_{0}.$时,θ和τ的值和一阶导数是准确的。
为了证明$\hat{x}$对其参数的功能依赖性,我们使用隐式微分 [1, 40],即区分方程 $f(\hat{\mathbf{x}};\theta)\equiv0\text{ w.r.t. }v,c,\theta$并求解 t 的导数。然后,可以检查等式 3 中的公式具有正确的导数。更多细节在补充材料中。我们将方程 3 实现为神经网络,即我们添加了两个线性层(参数为 c, v):
one before and one after the MLP f .等式 3 将 [1] 中的样本网络公式和 [40]DVR 中的可微深度统一起来,并将它们推广到考虑未知相机。$\hat{\mathbf{x}}$处的${\mathcal{S}}_{\theta}$的法向量可由下式计算:
$\hat{n}(\theta,\tau)=\nabla_{\mathbf{x}}f(\hat{x}(\theta,\tau),\theta)/\left|\nabla_{\mathbf{x}}f(\hat{\mathbf{x}}(\theta,\tau),\theta)\right|_{2}.$ Eq.4
请注意,对于 SDF,分母为 1,因此可以省略
Approximation of the surface light field
表面光场辐射 L 是从$\mathcal{S}_{\theta}$在$\hat{x}$处反射的光量,方向为 -v 到达 c。它由两个函数决定:描述表面的反射率和颜色属性的双向反射率分布函数 (BRDF) 和场景中发出的光(即光源)。
BRDF函数$B(x,\mathbf{n},\mathbf{w}^{o},\mathbf{w}^{i})$描述了反射亮度(即光通量)在某些波长(即颜色)下的比例,相对于从方向$w^{i}$的入射辐射的方向$w^{o}$处法向n离开表面点x。我们让 BRDF 也依赖于一个点处的法线到表面。场景中的光源由函数 $L^e(x,\mathbf{w}^o)$ 描述,该函数测量点 x 处某个波长的光在方向 $w^{o}$处的发射辐射。方向v到达c的光量等于方向$\mathbf{w}^o=-\mathbf{\upsilon}$中$\hat{x}$反射的光量,用所谓的渲染方程[21,17]描述:
$L(\hat{x},w^o)=L^e(\hat{x},w^o)+\int_{\Omega}B(\hat{x},\hat{n},w^i,w^o)L^i(\hat{x},w^i)(\hat{n}\cdot w^i)dw^i=M_0(\hat{x},\hat{n},v),$ Eq.5
其中$L^i(\hat{\mathbf{x}},\mathbf{w}^i)$编码方向$w^{i},$$\hat{x}$处的入射辐射,项$\hat{n}\cdot w^{i}$补偿光不正交地撞击表面的事实;Ω是以$\hat{n}$为中心的半球体。函数 $M_{0}$ 将表面光场表示为局部表面几何 $\hat{\mathbf{x}},\hat{\mathbf{n}},$和观察方向 v 的函数。该渲染方程适用于每个光波长;如后面所述,我们将将其用于红色、绿色和蓝色 (RGB) 波长。
我们将注意力限制在可以用连续函数 M0 表示的光场上。我们用 $\mathcal{P}=\{M_{0}\}$表示这种连续函数的集合(有关 P 的更多讨论,请参阅补充材料)。用(足够大的)MLP近似M(神经渲染器)替换$M_0$提供了光场近似:
$L(\theta,\gamma,\tau)=M(\hat{x},\hat{n},v;\gamma).$ Eq.6
几何和外观的解纠缠需要可学习的M来近似所有输入x, n, v的$M_0$,而不是记忆特定几何的亮度值。给定任意选择光场函数$M_{o}\in\mathcal{P}$,存在权重$\gamma=\gamma_{0}$的选择,使得M对于所有x, n, v(在某些有界集合中)近似于$M_0$。这可以通过 MLP 的标准普适定理来证明(详见补充)。然而,M 可以学习正确的光场函数 $M_0$ 的事实并不意味着在优化过程中保证学习它。然而,能够近似任意 x, n, v 的 M0 是解开几何(用 f 表示)和外观(用 M 表示)的必要条件。我们将此必要条件命名为 P-university。
Necessity of viewing direction and normal
对于 M 能够表示从表面点 x 反射的正确光,即 P-universal,它必须作为参数 v, n 接收。即使我们期望 M 适用于固定几何形状,观察方向 v 是必要的;例如,用于模拟镜面反射。另一方面,正常的 n 可以被 M 记忆为 x 的函数。然而,为了解开几何,即允许 M 独立于几何学习外观,还需要结合法线方向。这可以在图 3 中看到:
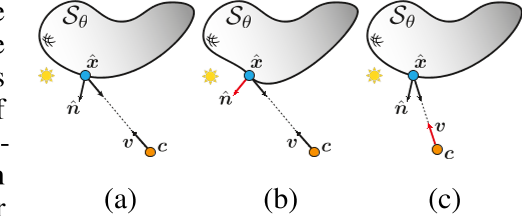
没有法线信息的渲染器M将在情况(A)和(b)中产生相同的光估计,而没有观看方向的渲染器M将在情况(A)和(c)中产生相同的光估计。在补充中,我们提供了这些渲染器在Phong反射模型下无法产生正确亮度的详细信息[8]。先前的作品,例如[40],已经考虑了$L(\theta,\gamma)=M(\hat{x};\gamma).$如上所述,从M中省略n和/或v将导致non-P-universal。在实验部分,我们证明了在渲染器M中加入n确实可以成功地解除几何和外观的纠缠,而忽略它则会损害解除纠缠。
Accounting for global light effects.
P-universal是学习一个可以从集合P中模拟外观的神经渲染器M的必要条件。然而,P不包括二次照明和自阴影等全局照明效果。我们通过引入一个全局特征向量来进一步提高IDR的表达能力。这个特征向量允许渲染器对几何$S_{\theta}$进行全局推理。为了得到向量z,我们将网络f扩展如下$F(x;\theta)=\left[f(x;\theta),z(x;\theta)\right]\in\mathbb{R}\times\mathbb{R}^{\ell}.$。一般来说,z可以编码相对于表面样本x的几何$S_{\theta}$;Z被馈送到渲染器中:$\hat{\mathbf{z}}(\theta,\tau)=\mathbf{z}(\hat{\mathbf{x}};\theta)$,以考虑与当前感兴趣的像素p相关的表面样本$\hat{\mathbf{x}}$。我们现在已经完成了IDR模型的描述,如公式2所示。
Masked rendering
另一种用于重建3D几何体的2D监督类型是遮罩;掩码是二值图像,表示对于每个像素p,感兴趣的对象是否占用该像素。掩码可以在数据中提供(如我们假设的那样),也可以使用掩码或分割算法计算。我们想考虑以下指示函数来识别某个像素是否被渲染对象占用(记住我们假设某个固定像素p):
$S(\theta,\tau)=\begin{cases}1&R(\tau)\cap\mathcal{S}_\theta\neq\emptyset\\0&\text{otherwise}\end{cases}$
由于这个函数在θ上不可微,在τ上也不可连续,我们使用一个几乎处处可微的近似:
$S_\alpha(\theta,\tau)=\text{sigmoid}\left(-\alpha\min_{t\geq0}f(c+t\mathbf{v};\theta)\right),$ Eq.7
其中α > 0是一个参数。由于按照惯例,几何内部f < 0,外部f > 0,因此可以证明$\begin{aligned}S_\alpha(\theta,\tau)\xrightarrow{\alpha\to\infty}S(\theta,\tau)\end{aligned}$。请注意,微分方程7w.r.t. ${\mathbf{c}},v$可以使用包络定理来完成,即$\partial_{\mathbf{c}}\operatorname{min}_{t\geq0}f(\mathbf{c}+t\mathbf{v};\theta)=\partial_{\mathbf{c}}f(\mathbf{c}+t_{x}\mathbf{v};\theta),$
其中$t_{x}$是达到最小值的参数,即$f(c_0+t_{x}v_0;\theta)=\min_{t\geq0}f(c_0+tv_0;\theta)$,$∂_{v}$也是类似的。因此,我们将$S_{\alpha}$实现为神经网络$\text{sigmoid}(-\alpha f(\mathbf{c}+t_{x}\mathbf{v};\theta)).$。注意这个神经网络在$c = c_{0}$和$v = v_{0}$处有精确的值和一阶导数。
Loss
设$\begin{aligned}I_p\in[0,1]^3,O_p\in\{0,1\}\end{aligned}$为相机$c_{p}(\tau)$和方向$v_{p}(\tau)$拍摄的图像中像素p对应的RGB和掩码值(resp.),其中$p∈P$表示图像输入集合中的所有像素,$\tau\in\mathbb{R}^k$表示场景中所有相机的参数。损失函数的形式是
$\mathrm{loss}(\theta,\gamma,\tau)=\mathrm{loss}_{\mathrm{RGB}}(\theta,\gamma,\tau)+\rho\mathrm{loss}_{\mathrm{MASK}}(\theta,\tau)+\lambda\mathrm{loss}_{\mathrm{E}}(\theta)$ Eq.8
我们在P的小批量像素上训练这个损失;为了使记号简单,我们用P表示当前的小批。对于每个$p∈P$,我们使用球体跟踪算法[12,20]来计算射线$R_p(\tau)$与$S_θ$的第一个交点$c_p+t_{p,0}v_p,$设$P^{\mathrm{in}}\subset P$是像素P的子集,其中存在交集且$O_p=1.\text{ Let }L_p(\theta,\gamma,\tau)=M(\hat{x}_p,\hat{n}_p,\hat{z}_p,v_p;\gamma),$其中,$\hat{x}_{p},\hat{n}_{p}$定义为式3和式4,$\hat{\mathbf{z}}_{p}=\hat{\mathbf{z}}(\hat{x}_{p};\theta)$如3.2节和公式2所示。
RGB损失为
$\mathrm{loss}_{\mathrm{RGB}}(\theta,\gamma,\tau)=\frac{1}{|P|}\sum_{p\in P^{\mathrm{in}}}\left|I_{p}-L_{p}(\theta,\gamma,\tau)\right|,$ Eq.9
$P^\mathrm{out}=P\setminus P^\mathrm{in}$表示小批中没有射线几何相交或$O_p = 0$的指标。掩膜损失是
$\mathrm{loss}_{\mathrm{MASK}}(\theta,\tau)=\frac1{\alpha|P|}\sum_{p\in I^{\mathrm{pout}}}\mathrm{CE}(O_{p},S_{p,\alpha}(\theta,\tau)),$ Eq.10
CE是交叉熵损失
最后,我们通过隐式几何正则化(IGR)使f近似为带符号距离函数[11],即结合Eikonal正则化
$\mathrm{loss}_{\mathrm{E}}(\theta)=\mathbb{E}_{\mathbf{x}}\big(\left|\nabla_{\mathbf{x}}f(x;\theta)\right|-1\big)^2$ Eq.11, 其中x均匀分布在场景的边界框中。
Implementation details
Experiments
Multiview 3D reconstruction
Dataset
- DTU
- MVS
Evaluation
- PSNR
- Chamfer-$L_1$
- compare with DVR、Colmap、Furu
- Quantitative results
Small number of cameras.