| Title | LoD-NeuS: Anti-Aliased Neural Implicit Surfaces with Encoding Level of Detail |
|---|---|
| Author | Zhuang, Yiyu and Zhang, Qi and Feng, Ying and Zhu, Hao and Yao, Yao and Li, Xiaoyu and Cao, Yan-Pei and Shan, Ying and Cao, Xun |
| Conf/Jour | arXiv |
| Year | 2023 |
| Project | NeIF (nju-3dv.github.io) |
| Paper | Anti-Aliased Neural Implicit Surfaces with Encoding Level of Detail (readpaper.com) |
AIR
我们提出了LoD-NeuS,一种用于高频几何细节恢复和抗锯齿新视图渲染的高效神经表示。从具有细节水平(LoD)的基于体素的表示中获得灵感,我们引入了一种基于多尺度三平面的场景表示,该场景表示能够捕获符号距离函数(SDF)的LoD和空间亮度。我们的表示从沿射线的截锥内的多卷积特征中聚集空间特征,并通过可微分渲染优化LoD特征体积。此外,我们提出了一种误差引导采样策略来指导优化过程中SDF的增长。定性和定量评估表明,与最先进的方法相比,我们的方法实现了更好的表面重建和逼真的视图合成。
- In particular, we firstly present a novel position encoding based on multi-scale tri-planes to enable continuous levels of details
- To alleviate aliasing, we consider the size of cast cone rays and specifically design multi-convolved features to approximate the cone sampling
- Meanwhile, we observe that thin surface reconstruction using SDF is challenging, thus propose a refined solution involving an error-guided sampling strategy to facilitate SDF growth
Method
Multi-scale Tri-plane Encoding
InstantNGP 哈希冲突、内存占用大
TensoRF 三平面编码 在处理复杂几何和有效的空间正则化方面提供了更大的灵活性,本文将多尺度三平面表示合并到一个基于neus的框架中,用于复杂的表面重建和高质量的渲染。
多分辨率三平面:$\{R_{l}\}_{l=1}^{L}$
级联特征与输入的x:$\mathbf{\vec{F}}=(\mathbf{x},\mathbf{F}_1,…,\mathbf{F}_L),$
Anti-aliasing Rendering of Implicit Surfaces
NeuS没有考虑像素的形状,这种近似可能导致高频信息的欠采样或模糊表示,并导致混叠伪影。为了缓解这个问题,我们通过将射线定义为圆锥体来重新制定体渲染,同时考虑到像素大小。这样可以实现连续的LoD,并从欠采样图像中恢复高质量的SDF,从而更准确地捕获和重建场景的细节。
- 超采样,将锥体光线离散成一批光线,计算成本和时间成本高
- Cone Discrete Sampling.锥采样:通过相机像素的投射锥射线被划分为一系列锥形截体
- Mip-NeRF侧重于以不同分辨率渲染场景,而不是恢复场景细节
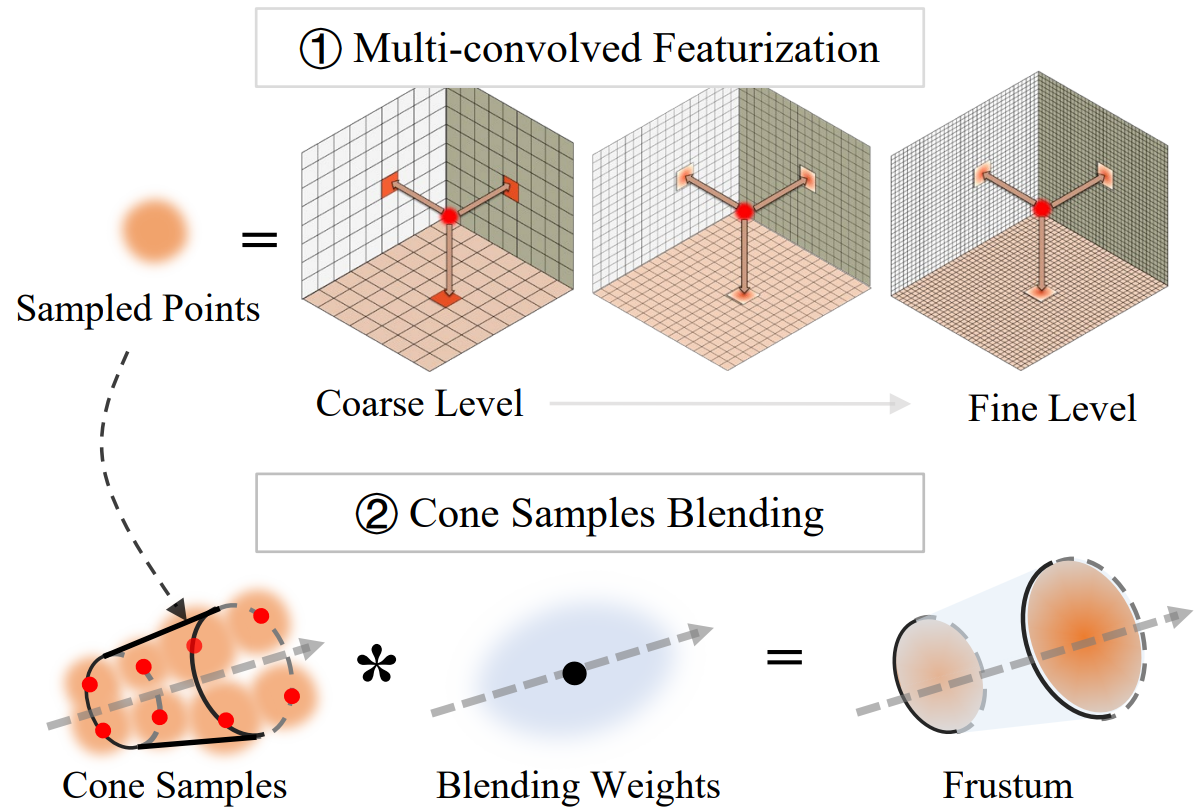
- 利用我们基于三平面的表示,我们通过像素角投射了四条额外的光线,从而考虑了像素的大小和形状。然后,沿锥体的每个锥形截锥由八个顶点表示。给定任何三维采样位置x在一个锥形截体内,我们使用递减权值混合每个顶点$x_𝑣$的三平面特征,$W(\mathbf{x},\mathbf{x}_{\boldsymbol{\upsilon}})=\exp(-k|\mathbf{x}_{\boldsymbol{\upsilon}}-\mathbf{x}|),$ 它随着顶点x𝑣与采样点x之间的距离而减小。𝑘是一个可学习的参数,我们最初将其设置为80,并在训练期间与其他参数一起更新。重要的是要注意,递减函数应该意识到锥形截锥体的大小。锥台越小,函数衰减越快
- Mulit-convolved Featurization.
- 虽然利用相邻顶点沿相邻射线的多尺度特征进行圆锥采样,但由于圆锥截体内的样本稀疏,这种近似可能不够。一种直接的方法是引入更多离散样本,但这会增加计算成本和内存负担。
- 利用每个三平面的二维高斯函数来表示圆锥截锥体应该集成的区域。结合我们的锥形离散采样,我们提出了一个多重高斯卷积特征来表示邻近顶点的特征,这些顶点近似于采样点及其相应的锥形截锥体
- $\mathbf{G}_{\boldsymbol{\upsilon}}(\mathbf{x}_{\boldsymbol{\upsilon}})=G(\vec{\mathbf{F}}_{\boldsymbol{\upsilon}},\{\tau_{\boldsymbol{\upsilon}}\}_{\boldsymbol{l}=1}^{L})=\sqcup_{\boldsymbol{l}=1}^{L}\mathcal{G}\left(\mathbf{F}_{\boldsymbol{l}},\tau_{\boldsymbol{l}}\right),$
- $\mathrm{Z}(\mathrm{x})=\sum_{v=1}^VW(\mathrm{x},\mathrm{x}_v)\mathrm{G}_v(\mathrm{x}_v),$ V=8为圆锥体的顶点数
Training and Loss
$L_{rgb}=\frac{1}{n}\sum_{p}\left|\hat{C_{p}}-C_{p}\right|_{1}.$
$L_{eikonal}=\frac{1}{nm}\sum_{i}(|\nabla f(x_{i})|_{2}-1)^{2}.$
$L_{mask}=\frac{1}{n}\sum_{p}\mathrm{BCE}(M_{p},\hat{O}_{p}),$
其中opacity:$\hat{O}_k=\sum_j^mT_j(1-\exp(-\sigma_j\delta_j))$
SDF Growth Refinement
- 表示一个薄物体需要在SDF中快速翻转,这对于神经网络来说是困难的
- 与其他区域相比,薄物体对应的图像区域可能具有更少的样本,使其更难学习
一个直接的解决方案可能是增加该区域周围的采样频率,但只有位于该区域周围的采样射线被证明有助于这种重建
本文利用来自2D图像的信息,从缺失的细段与表面相遇的空间点引导SDF生长
- 我们在每个训练视点呈现训练后的SDF,使用L1距离对输入计算误差图,顺序二值化该图并将其扩展到候选区域𝑀𝑒。为了找到我们的生长方法的起点,我们使用Zhou等人方法(End-to-End Wireframe Parsing)来检测线端点并将其扩展到我们选择的区域𝑀𝑠
Experiments
Baseline:NeuS、HF-NeuS、NeRF
Metrics:PSNR、CD
Datasets:DTU(with mask)