Title	MonoSDF: Exploring Monocular Geometric Cues for Neural Implicit Surface Reconstruction
Author	Zehao Yu1 Songyou Peng2,3 Michael Niemeyer1,3 Torsten Sattler4 Andreas Geiger1,3
Conf/Jour	NeurIPS
Year	2022
Project	MonoSDF (niujinshuchong.github.io)
Paper	MonoSDF: Exploring Monocular Geometric Cues for Neural Implicit Surface Reconstruction (readpaper.com) [MonoSDF: Exploring Monocular Geometric Cues for Neural Implicit Surface Reconstruction \	PDF](https://arxiv.org/pdf/2206.00665)

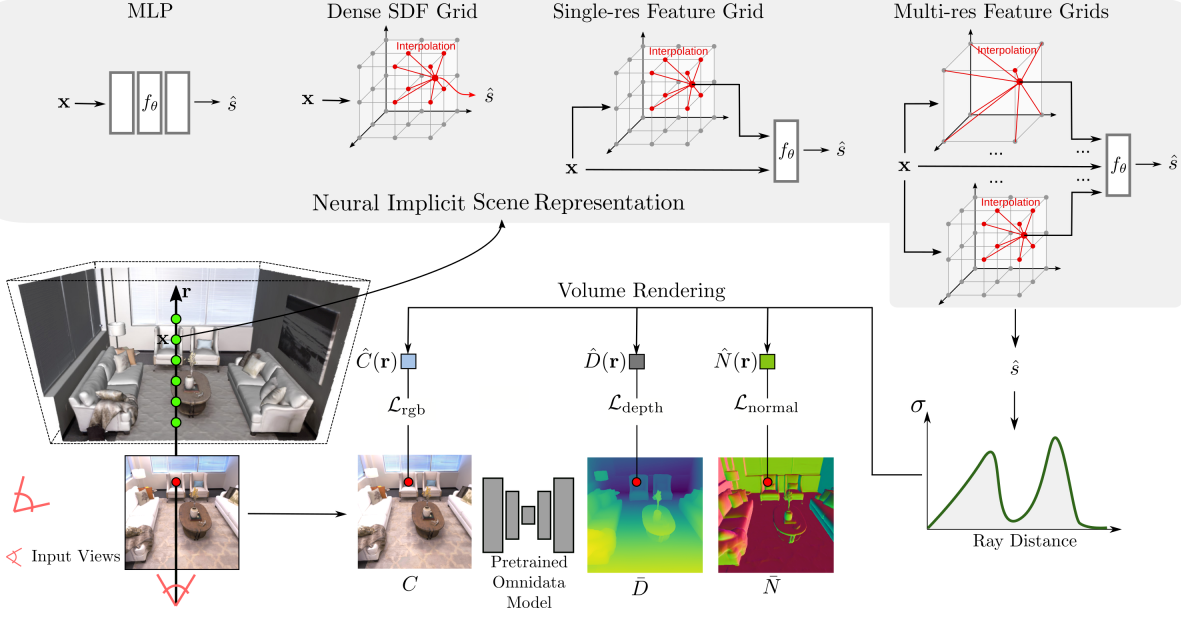
深度+法向量监督

AIR

目前的 neural implicit surface reconstruction方法无法处理大的、复杂的和稀疏视图的场景重建。主要是由于RGB 重建loss的内在模糊性无法提供足够的约束，in particular in less-observed and textureless areas

本文 demonstrate that depth and normal cues, predicted by general-purpose monocular estimators, significantly improve reconstruction quality and optimization time. 都有着提升

不管是什么表示方法：monolithic MLP models over single-grid to multi-resolution grid representations.
也不管是什么场景：small-scale single-object as well as large-scale multi-object scenes

Method

Implicit scene representations：$f:\mathbb{R}^3\to\mathbb{R}\quad\mathrm{~x}\mapsto s=\mathrm{SDF}(\mathbf{x})$ 根据3Dpoint 坐标得到该点的SDF值

SDF Prediction

Dense SDF Grid
Single MLP
Single-Resolution Feature Grid with MLP Decoder
Multi-Resolution Feature Grid with MLP Decoder

Color Prediction：$\hat{\mathbf{c}}=\mathbf{c}_\theta(\mathbf{x},\mathbf{v},\hat{\mathbf{n}},\hat{\mathbf{z}})$

其中$\hat{\mathbf{n}}$为SDF函数的分析梯度 torch.autograd.grad
特征向量$\hat{\mathbf{z}}$为SDF网络的输出

Volume Rendering of Implicit Surfaces (VolSDF)

Density values $\sigma_\beta(s)=\begin{cases}\frac{1}{2\beta}\exp\left(\frac{s}{\beta}\right)&\text{if} s\leq0\\\frac{1}{\beta}\left(1-\frac{1}{2}\exp\left(-\frac{s}{\beta}\right)\right)&\text{if} s>0\end{cases}$ $\beta$ 是一个可学习的参数
$\hat{C}(\mathbf{r})=\sum_{i=1}^MT_\mathbf{r}^i\alpha_\mathbf{r}^i\hat{\mathbf{c}}_\mathbf{r}^i$
$T_\mathbf{r}^i=\prod_{j=1}^{i-1}\left(1-\alpha_\mathbf{r}^j\right)$
$\alpha_\mathbf{r}^i=1-\exp\left(-\sigma_\mathbf{r}^i\delta_\mathbf{r}^i\right)$

rendering 深度or法向量

$\hat{D}(\mathbf{r})=\sum_{i=1}^MT_\mathbf{r}^i \alpha_\mathbf{r}^i t_\mathbf{r}^i$
$\hat{N}(\mathbf{r})=\sum_{i=1}^MT_\mathbf{r}^i \alpha_\mathbf{r}^i \hat{\mathbf{n}}_\mathbf{r}^i$

guided 深度or法向量：使用 pretrained Omnidata model 来当作 monocular depth/normal map predictor

损失函数：$\mathcal{L}=\mathcal{L}_\mathrm{rgb}+\lambda_1\mathcal{L}_\mathrm{eikonal}+\lambda_2\mathcal{L}_\mathrm{depth}+\lambda_3\mathcal{L}_\mathrm{normal}$

$\mathcal{L}_{\mathrm{rgb}}=\sum_{\mathbf{r}\in\mathcal{R}}\left|\hat{C}(\mathbf{r})-C(\mathbf{r})\right|_1$
$\mathcal{L}_{\mathrm{eikonal}}=\sum_{\mathbf{x}\in\mathcal{X}}(\left|\nabla f_\theta(\mathbf{x})\right|_2-1)^2$
$\mathcal{L}_{\mathrm{depth}}=\sum_{\mathbf{r}\in\mathcal{R}}\left|(w\hat{D}(\mathbf{r})+q)-\bar{D}(\mathbf{r})\right|^2$
- $w$ and $q$ are scale and shift used to aligh $\hat{D}$与$\bar{D}$ 每个batch需要被独立估计??
- $(w,q)=\underset{w,q}{\arg\min}\sum\limits_{\mathbf{r}\in\mathcal{R}}\Big(w\hat{D}(\mathbf{r})+q-\bar{D}(\mathbf{r})\Big)^2$ solve w and q with a least-squares criterion
- $\mathbf{h}^{\mathrm{opt}}=\underset{\mathbf{h}}{\operatorname*{\arg\min}}\sum_{\mathbf{r}\in\mathcal{R}}\left(\mathbf{d}_{\mathbf{r}}^T\mathbf{h}-\bar{D}(\mathbf{r})\right)^2$ $:\text{Let h}=(w,q)^T\text{ and }\mathbf{d_r}=(\hat{D}(\mathbf{r}),1)^T$
- $\mathbf{h}=\left(\sum_\mathbf{r}\mathbf{d_r}\mathbf{d_r}^T\right)^{-1}\left(\sum_\mathbf{r}\mathbf{d_r}\bar{D}(\mathbf{r})\right)$
- 对一个从单张图中随机采样光线的一个batch必须被独立估计由于depth maps predicted by the monocular depth predictor can differ in scale and shift and the underlying scene geometry changes at each iteration.
$\mathcal{L}_{\mathrm{normal}}=\sum_{\mathrm{r}\in\mathcal{R}}|\hat{N}(\mathbf{r})-\bar{N}(\mathbf{r})|_1+|1-\hat{N}(\mathbf{r})^\top\bar{N}(\mathbf{r})|_1$

Experiments

深度图的作用没那么明显，并且depth和normal先验都无法重建出开关处的细节

Discussion

Future：

使用更加精确的 depth or normal estimator
exploring other cues such as occlusion edges, plane, or curvature is an interesting future direction
更加高分辨率的 depth or normal cues
相机噪声Joint optimization of scene representations and camera parameters [4, 92] is another interesting direction, especially for multi-resolution grids, in order to better handle noisy camera poses.