| Title | NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis |
|---|---|
| Author | Ben Mildenhall*Pratul P. Srinivasan*Matthew Tancik*Jonathan T. BarronRavi RamamoorthiRen Ng |
| Conf/Jour | ECCV 2020 Oral - Best Paper Honorable Mention |
| Year | 2020 |
| Project | NeRF: Neural Radiance Fields (matthewtancik.com) |
| Paper | NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis (readpaper.com) |
NeRF(Neural Radiance Fields)是一种用于生成逼真三维场景的计算机图形学方法。通过神经网络对场景中的每个空间点进行建模,NeRF可以估计每个点的颜色和密度信息。利用渲染方程,NeRF能够合成高质量的逼真图像。相较于传统的渲染方法,NeRF能够处理复杂的光照和反射效果,广泛应用于虚拟现实、增强现实、电影制作和游戏开发等领域。然而,NeRF方法仍面临一些挑战,如计算复杂度和对训练数据的依赖性。研究人员正在不断改进NeRF,以提高其效率和扩展性。
其他参考文献
大佬的公式推导+代码分析NeRF: A Volume Rendering Perspective | Will (yconquesty.github.io)
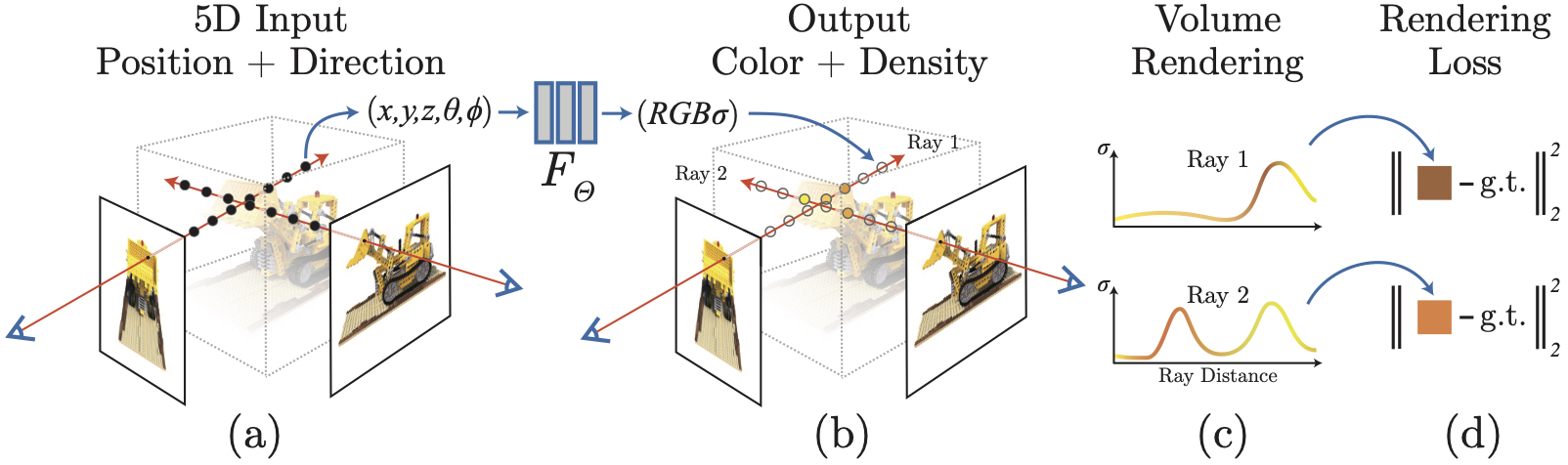
输入多张不同视角的图片,通过训练出的MLP模型$F_{\theta}$,输出一个隐式表达的模型,该模型包含粒子的坐标、颜色和不透明度等信息。通过体渲染函数生成新视角的图片。
原理:
- 从相机原点出发,经过图片上的某点像素,生成一条光线 $r(t)=\textbf{o}+t \textbf{d}$ ,$\textbf{o}$为相机原点,$\textbf{d}$为光线的方向向量。
- 在光线上采样N个点,并得到这些点(粒子)的空间坐标xyz,同一条光线上,通过d也可得出粒子的方向坐标$(\theta,\phi)$。
- 对粒子坐标$(x,y,z,\theta,\phi)$做位置编码,将低维信息转化为高维的信息。(神经网络在表示颜色和几何形状的高频变化方面表现不佳。他人的研究也表明深度神经网络倾向于学习低频信息,可以通过在输入之前将高频函数映射到高维空间的方法来增强高频信息的拟合能力。)
- 构建MLP网络,输入为粒子坐标的高维信息,输出为粒子的RGB颜色和不透明度,然后根据体渲染函数,由粒子的RGB和不透明度计算出图片像素的颜色值。loss为该图片像素颜色和ground truth的均方差损失。
- 根据粗采样后得到的网络,进行精采样。由粗网络得到的点云模型,根据体渲染函数,计算出权重,对权重大的地方,采样的点多一点,根据精采样+粗采样得到的粒子,重复3、4步,最后训练出一个更精细的网络模型。
- 多张不同视角图片—>MLP网络—>隐式点云模型,确定的相机位姿—>生成光线得到点云的坐标—>隐式点云模型—>点云的密度和颜色—>新视角图片
隐式表达模型:输入的是点云的位置坐标信息,输出时该点的不透明度和颜色值。根据某个确定的相机位姿以及图片的大小,每个像素生成一条光线,并在光线上进行采样得到点云,根据点云中每个点的位置坐标进行编码并输入进网络得到该点的密度值和颜色值,然后通过体渲染函数,计算出每个像素点处的颜色值,最终得到一张新视角出的图片。
体渲染函数
T(t):$t_{n}$到t的透明度的累计
- 光线距离越远 $\int_{t_n}^t\sigma(\mathbf{r}(s))ds$ 越大,T(t)就越小
- T(t)作用:离相机近的不透明的粒子,会遮挡住后面的粒子,在渲染时的权重较大
- 类似:无偏,给定一束光线,在其表面处的点,占得权重应该最大;此外如果两个点,后面被前面堵塞,那么模型应该可以感知到。具体来说,前面的权重应该大于后面的权重。
主要思想:分段连续
离散化:
某个点的不透明度 $\sigma_i$
该点与相邻点之间的距离 $\delta_{i} = t_{i+1} - t_{i}$
体渲染函数根据光线上采样点的RGB和不透明度,得到该光线所经过的图片像素的颜色值。
位置编码
神经网络在表示颜色和几何形状的高频变化方面表现不佳。他人的研究也表明深度神经网络倾向于学习低频信息,可以通过在输入之前将高频函数映射到高维空间的方法来增强高频信息的拟合能力。
- 空间坐标xyz,L=10,10组sin和cos,总共转化为
20*3=60个向量 - 方向两项$\theta \phi$,L=4,4组sin和cos,总共转化为
8*3=24个向量(为了方便计算,使用相机7的xyz参数替代)
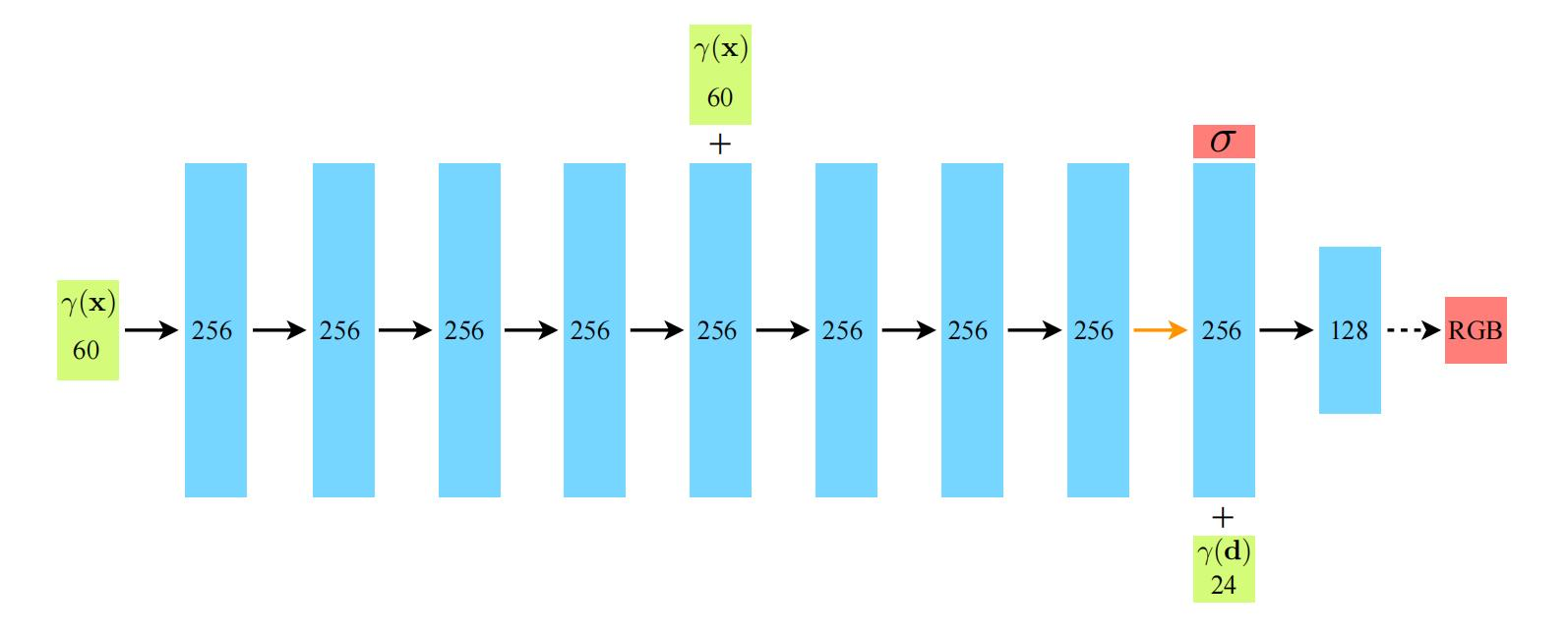
神经网络
网络:MLP
输入:$(x,y,z,\theta,\phi)$编码后的信息
- 粒子的空间坐标 xyz
- 粒子的方向坐标 $(\theta,\phi)$
输出:$R G B$ ${\sigma}$
- 粒子的RGB颜色,由空间和方向信息共同得出
- 粒子的不透明度${\sigma}$,仅由空间信息得出,粒子的不透明度与观察方向无关
分层采样
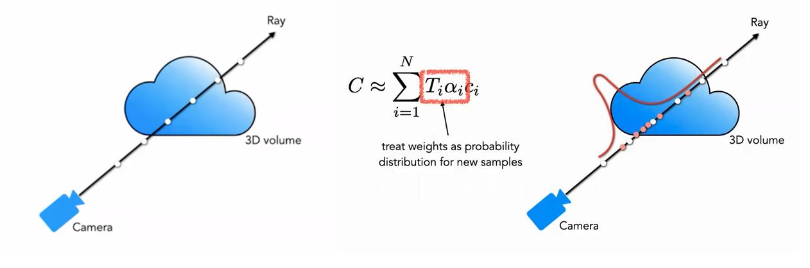
目的:目标区域采样点多,其他区域采样点少
粗网络采样:$N_{c}$
采样$N_{c}$个点:
对权重作标准化:
产生沿射线的分段常数概率分布函数(piecewise-constant PDF),从此分布中,利用逆变换采样采样出$N_{f}$个位置
精网络采样:
使用所有的$N_{c}$和$N_{f}$来计算最终的渲染颜色
参考资料
- Video:
NeRF源码解析_哔哩哔哩_bilibili
论文解读:《NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis》 - 知乎 (zhihu.com)
【原创】NeRF 三维重建 神经辐射场 建模 算法详解 NeRF相关项目汇总介绍。_哔哩哔哩_bilibili
光线采集+归一化采样点_哔哩哔哩_bilibili- Blog:
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
逆变换采样 - 知乎 (zhihu.com)
NeRF 的实现过程 - 知乎 (zhihu.com)
新视角合成 (Novel View Synthesis) - (4) NeRF 实现细节 - 知乎 (zhihu.com)
计算机图形学 - 知乎 (zhihu.com)
光线生成
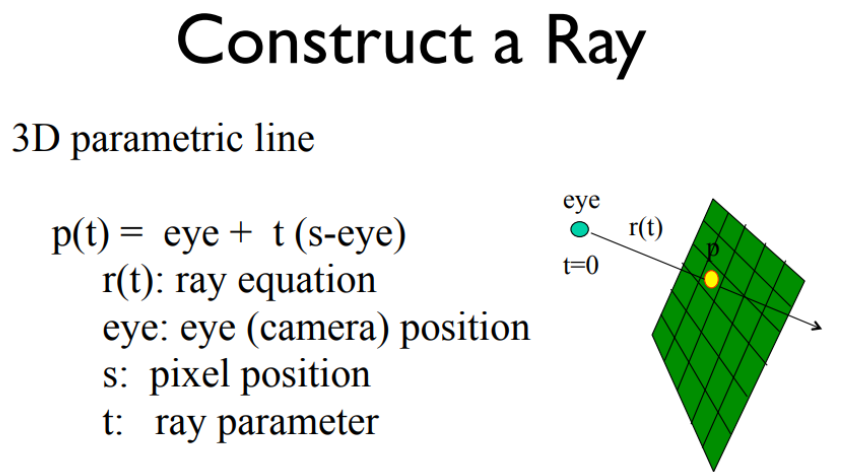
$r(t)=\textbf{o}+t\textbf{d}$ ,$\textbf{o}$是相机原点,$\textbf{d}$为方向向量
t通过 $t_{i} \sim \mathcal{U}\left[t_{n}+\frac{i-1}{N}\left(t_{f}-t_{n}\right), t_{n}+\frac{i}{N}\left(t_{f}-t_{n}\right)\right]$ ,在 $t_{near}$ 和 $t_{far}$ 之间,等间距获取N个点
根据相机原点和图片上随机一点像素,生成一条光线,并将该光线的坐标转换到世界坐标系。
已知:图片大小,所选图片上的像素位置,相机参数(焦距、相机位姿)。光线经过坐标变换:图片二维的像素坐标构建—>相机三维坐标—>世界坐标,得到光线在世界坐标系下的原点和方向向量, 然后对ray_o和ray_d进行NDC坐标变换,将锥形区域变换为一个2x2x2的正方体区域。(LLFF数据集)
从世界坐标系到相机坐标系的投影我们称为相机外参矩阵(反之为相机姿态矩阵),而从相机坐标系到像素坐标系的投影我们称为相机内参矩阵(用K来表示,由相机焦距与中心点决定)。旷视3d CV master系列训练营三:NeRF在实际场景中的应用 - 知乎 (zhihu.com)
图片二维坐标—>相机三维坐标 $X_{c}, Y_{c},Z_{c}$
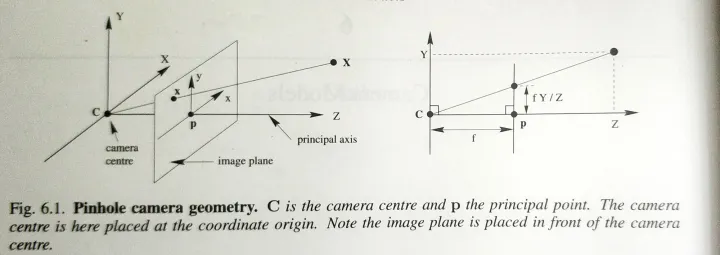
1 | 相机内参矩阵 |
相机三维坐标—>世界三维坐标XYZ
NeRF: How NDC Works | Will (yconquesty.github.io)
计算机图形学二:视图变换(坐标系转化,正交投影,透视投影,视口变换) - 知乎 (zhihu.com)
NDC 标准化设备坐标系
相机坐标系中坐标—>投影变换—>NDC中坐标
NeRF中是直接从世界坐标系转换到的NDC中的坐标
Projection transformation 分为 透视变换和正交变换
透视投影变换
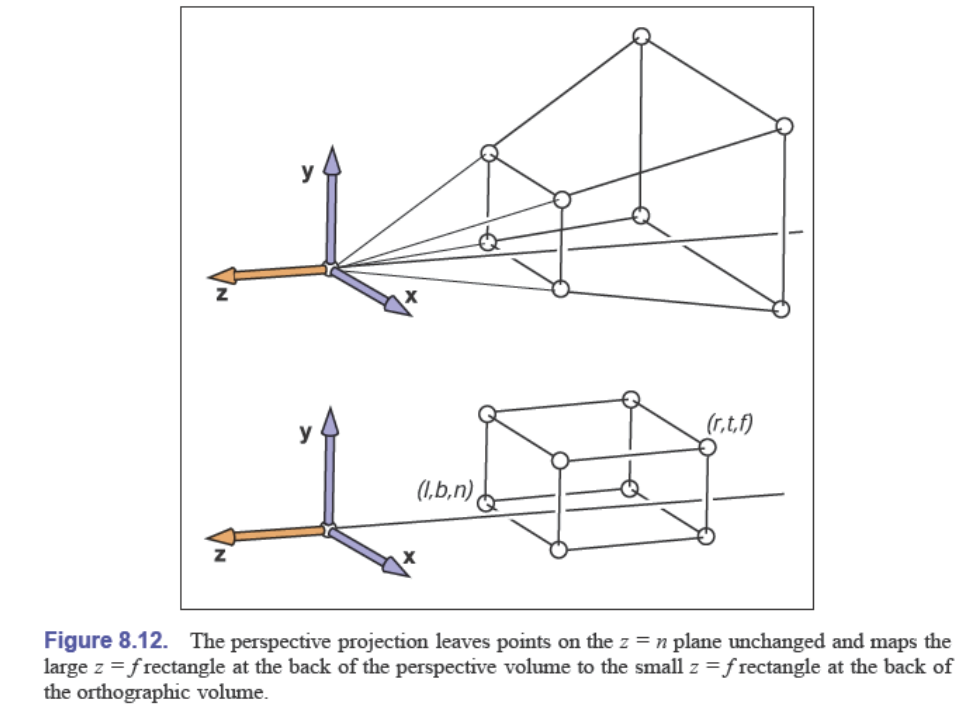
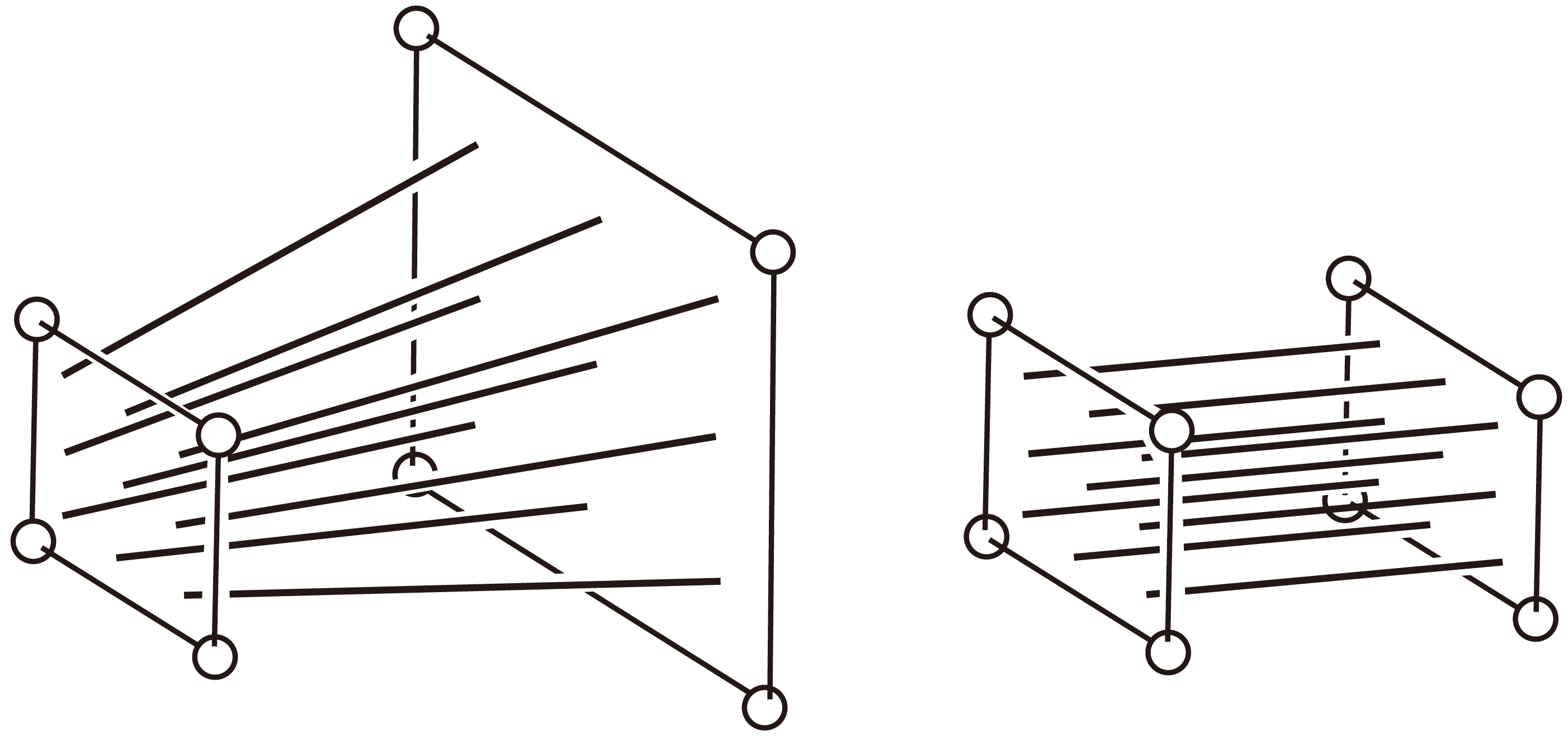
正交投影变换
光线平行,将原空间中物体,变换到一个2x2x2的立方体中
投影变换矩阵
将齐次坐标左乘投影矩阵,即可得到在NDC下的坐标:
因此对于光线:
$\begin{pmatrix}a_x\frac{o_x+td_x}{o_z+td_z}\\ a_y\frac{o_y+td_y}{o_z+td_z}\\ a_z+\frac{b_z}{o_z+td_z}\end{pmatrix}=\begin{pmatrix}o_x’+t’d_x’\\ o_y’+t’d_y’\\ o_z’+t’d_z’\end{pmatrix}.$
其中:
$\begin{aligned}&a_{x} :=-\frac{n}{r} \\&a_y :=-\frac nt \\&a_z :=\frac{f+n}{f-n} \\&b_z :=\frac{2nf}{f-n}\end{aligned}$
$\mathbf{o}’=\begin{pmatrix}o’_x\\ o’_y\\ o’_z\end{pmatrix}=\begin{pmatrix}a_x\frac{o_x}{o_z}\\ a_y\frac{o_y}{o_z}\\ a_z+\frac{b_z}{o_z}\end{pmatrix}=\pi(\mathbf{o}).$
交换顺序:
可得:
$\begin{aligned}& t^{\prime}=\frac{t d_{z}}{o_{z}+t d_{z}}=1-\frac{o_{z}}{o_{z}+t d_{z}} \\& \mathbf{d}^{\prime}=\left(\begin{matrix}{a_{x}\left(\frac{d_{x}}{d_{z}}-\frac{o_{x}}{o_{z}}\right)}\\ {o_{y}\left(\frac{d_{y}}{d_{z}}-\frac{o_{y}}{o_{z}}\right)}\\ {-b_{z}\frac{1}{o_{z}}}\end{matrix}\right). \end{aligned}$
又由:
$\begin{aligned}a_{x}& =-\frac{n}{r}=\frac{f_\mathrm{camera}}{\frac{W}{2}} \\a_y& =-\frac{n}{t}=\frac{f_{\mathrm{camera}}}{\frac{H}{2}} \\\lim\limits_{f\to\infty}a_z& =\lim\limits_{f\to\infty}\frac{f+n}{f-n}=1 \\\lim\limits_{f\to\infty}b_z& =\lim\limits_{f\to\infty}-\frac{2nf}{n-f}=2n \end{aligned}$
结果:
- in NeRF :
One final detail in our implementation: we shift o to the ray’s intersection with the near plane at z = −n (before this NDC conversion) by taking on = o + tndfor tn = −(n + oz )/dz . Once we convert to the NDC ray, this allows us to simply sample t′ linearly from 0 to 1 in order to get a linear sampling in disparity fromn to ∞ in the original space. - TL;DR: 在NDC变换之前,将o移动到近平面z=-n的地方,令near=0,因此可以简单的从0线性采样t’到1,以便在原始空间中从 n 到 ∞ 的视差中获得线性采样
- 对应代码中的ndc_rays函数