| Title | Strivec: Sparse Tri-Vector Radiance Fields |
|---|---|
| Author | Quankai Gao and Qiangeng Xu and Hao su and Ulrich Neumann and Zexiang Xu |
| Conf/Jour | ICCV |
| Year | 2023 |
| Project | Zerg-Overmind/Strivec (github.com) |
| Paper | Strivec: Sparse Tri-Vector Radiance Fields (readpaper.com) |
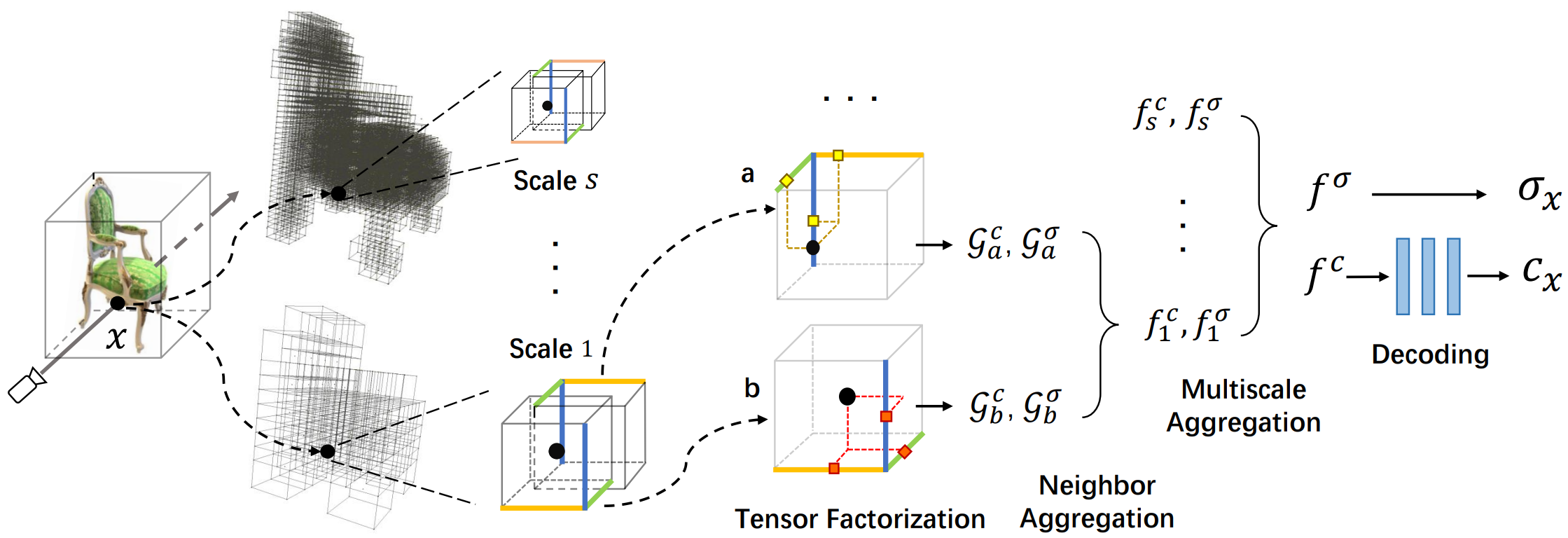
- 局部CP分解,三向量
- 多尺度,占用网格方式
Conclusion
在这项工作中,我们提出了一种高质量的神经场景重建和逼真的新视图合成的新方法。我们提出了一种新的基于张量分解的场景表示,它利用CP分解将3D场景紧凑地建模为表达局部亮度场的多尺度三向量张量的稀疏集。我们的表示利用了稀疏性和空间局部一致性,并导致复杂场景几何和外观的准确和有效的建模。我们证明了稀疏的三向量辐射场可以比以前最先进的神经表示(包括TensoRF和iNGP)获得更好的渲染质量,同时使用更少的参数。
AIR
我们提出了Strivec,一种新的神经表示,它将3D场景建模为具有稀疏分布和紧凑分解的局部张量特征网格的辐射场。我们的方法利用张量分解,在最近的工作TensoRF[7]之后,对张量网格建模。与使用全局张量并专注于其向量矩阵分解的TensoRF相反,我们建议使用局部张量云并应用经典的CANDECOMP/PARAFAC (CP)分解[5]将每个张量分解为三个向量,这些向量表示沿空间轴的局部特征分布并紧凑地编码局部神经场。我们还应用多尺度张量网格来发现几何和外观的共性,并利用三向量分解在多个局部尺度上的空间一致性。
最终的亮度场属性是通过聚合神经特征从多个局部张量在所有尺度上回归。我们的三向量张量稀疏分布在实际场景表面周围,通过快速粗重建发现,利用3D场景的稀疏性。我们证明了我们的模型可以在使用比以前的方法(包括TensoRF和InstantNGP)更少的参数的情况下获得更好的渲染质量[27]。
Introduction
NeRF,将3D场景表示为亮度场[26]已经实现了逼真的渲染质量,并成为3D视觉和图形应用中流行的设计选择。
TensoRF[7]和Instant-NGP[27],已经证明了在速度,紧凑性和质量方面使用共享全局特征编码进行辐射场建模的优势。然而,这些方法在场景中均匀地共享和分配神经特征(使用张量因子或哈希表),假设场景内容在整个空间中同样复杂,这可能是低效的(需要高模型容量),无法准确地模拟复杂的局部场景细节(见图1)。
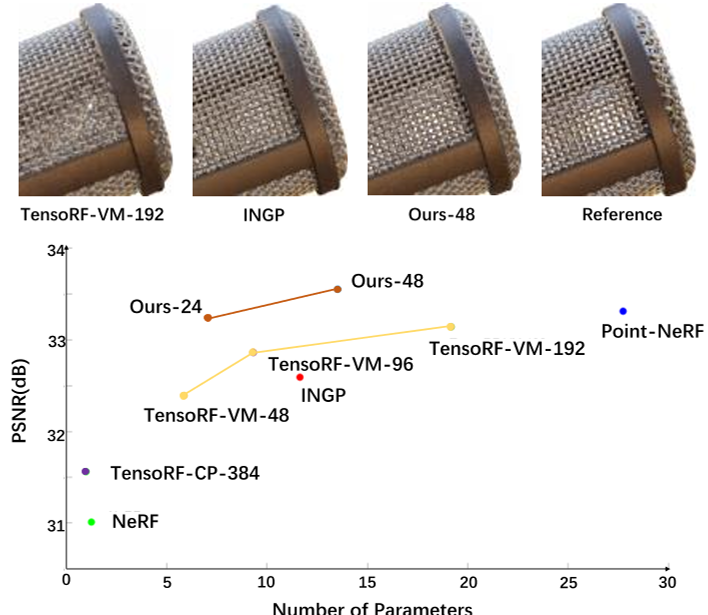
我们的目标是准确而紧凑地建模一个3D场景,并重现复杂的局部细节。为此,我们提出了Strivec,一种新的神经场景表示,它利用稀疏分布和紧凑分解的局部张量网格来模拟高质量的新视图合成的体积辐射场。如图1所示,我们的方法能够准确地模拟出复杂的场景结构,而这些结构是以前的方法无法很好地恢复的。更重要的是,我们卓越的渲染质量是用更少的模型容量实现的。
- TensoRF应用CP和向量矩阵(VM)分解技术将一个场分解为向量和矩阵,并将整个场景建模为一个全局分解张量
- TensoRF中的全局CP分解导致了一个高度紧凑的模型,但无法达到与VM分解相当的渲染质量。这是因为三向量CP分量是一级的,而整个3D场景的全局特征网格通常是复杂和高秩的,需要大量(不切实际的)CP分量来实现高精度。TensoRF通过在VM分解中引入矩阵因子来解决这个问题,本质上是增加每个张量分量的秩。
- 我们利用分布在场景表面周围的多个小局部张量的稀疏集来代替单个全局张量,以实现更有效的场景建模。具体来说,我们的每个张量都表示其局部边界框内的局部辐射场,并基于CP分解用分解的三重向量紧凑建模。
- 我们的模型由多个小张量网格组成,利用场景中的局部空间共性。与全局张量相比,我们的局部张量不那么复杂,等级也低得多,从而有效地减少了所需的CP分量(每个张量)的数量,并通过高度紧凑的三向量因子实现了实际的高质量辐射场重建。与TensoRF的VM模型相比,我们的局部三向量张量可以带来更好的渲染质量和紧凑性(见图1)。我们还观察到,我们的局部张量在空间轴方向上通常比全局张量更robust(这会影响张量的秩,从而影响质量;见图2)
重要的是,采用局部张量(而不是全局张量)也使我们能够根据实际场景分布灵活地分配神经特征,从而比全局表示更有效地进行场景建模和更好地利用模型参数。为此,我们预先获取粗糙的场景几何形状——这可以通过快速RGBσ体积重建(如DVGO[36])或多视图立体(如Point-NeRF[43])轻松实现——直接在实际场景表面周围分布局部张量,从而产生稀疏的场景表示,避免不必要地对空场景空间进行建模。请注意,虽然以前的方法也利用了辐射场的稀疏表示(使用体素[22,45]Plenoxels或Point-NERF[43]),但它们的局部特征是独立建模和优化的。
我们的模型将局部框内的一组局部特征关联起来,并用三向量紧凑地表示它们,独特地利用了沿轴的局部空间相干性,并通过张量分解在特征编码中施加了局部低秩先验。此外,与以往仅使用单尺度特征网格或点云的稀疏表示不同,我们通过分布多尺度局部张量,以分层方式在多尺度上有效地建模场景几何和外观。特别是,对于任意的3D位置,我们在所有尺度上聚合其相邻三向量分量的神经特征,并从聚合特征中解码体积密度和视图相关颜色,用于亮度场渲染。
我们的方法采用了最好的以前的局部和全局的亮度场表示。与TensoRF和Instant-NGP等全局表示相比,我们的模型更直接地利用了场景的稀疏性;与Plenoxels和PointNeRF等局部表示相比,我们的模型利用了场景几何和外观的局部平滑性和一致性。正如我们在合成数据集和真实数据集上的实验结果所示,我们的模型能够在这些数据集上实现最先进的渲染质量,优于以前的方法,包括TensoRF和Instant-NGP,同时使用更少的模型参数,展示了我们模型的优越表征能力。
Related Work
Scene representations.
为了表示三维场景,传统的和基于学习的方法研究了各种表示方法,如深度图[16,21]、网格[18,40,34]、点云[32,1,39]和隐式函数[10,25,28,44]。近年来,连续神经场表征在单视图三维重建[42,14]、曲面补全[11,30]、多视图重建[28]和新视图合成[26,24]等各种三维任务中表现突出。与传统的离散表示相比,连续场不受空间分辨率的限制,例如体积分辨率或点的数量。它也可以自然地用神经网络来表示,比如MLP,它以很好地逼近复杂函数而闻名。
Neural field representations.
具体来说,NeRF[26]将3D场景表示为具有全局坐标MLP的亮度场,它联合建模几何、光照和纹理信息,从而在新颖的视图合成中实现了逼真的渲染质量。除了其优势外,纯粹基于mlp的NeRF模型[3,38]在建模高度复杂或大规模场景时,由于模型容量有限,优化速度慢,以及建模空白空间的成本,通常存在效率低下的问题[2]。
为了更有效地建模辐射场,最近的工作已经探索了将神经场与各种传统的3D表示相结合,包括体素[22,45,36,48]和点[43]。还研究了低秩表示,如三平面[6,13]和张量分解[7,29]。
特别是,DVGO[36]和Plenoxels[45]分别使用具有神经特征的密集体素和稀疏体素进行辐射场建模。虽然优化效率高,但这些基于局部特征网格的表示导致模型尺寸较大,并且在特征分辨率非常高时可能面临过拟合问题。因此,DVGO也可以与低分辨率网格一起工作,而Plenoxels需要额外的空间正则化条款。
另一方面,最近的研究采用全局特征编码来表达高分辨率特征网格,包括将空间特征散列成多尺度哈希表的Instant-NGP[27]和将特征网格分解成矢量和矩阵因子的TensoRF[7]。这些全局特征编码方法利用了整个场景空间的空间相关性,导致了快速和紧凑的重建,并且在渲染质量上超越了以前基于mlp或基于网格的表示。然而,与NeRF类似,当表示高度复杂或大规模的内容时,这种全局表示也会受到其模型容量的限制。
相反,我们的方法结合了局部和全局代表。我们的三向量场在场景中是稀疏分布的,类似于局部表示(如plenoxels和Point-NeRF); 同时,像TensoRF一样,每个域的特征由局部区域共享的三向量分量表示,利用了空间特征的共性。我们的模型利用了空间稀疏性和相干性,比以前的局部和全局表示具有更高的紧凑性和更好的重建质量(见表1)。
与我们的工作相关,以前的方法,如KiloNeRF[33]和BlockNeRF[37]也利用多个本地mlp来表示一个场景。具体来说,KiloNeRF关注和加速NeRF,牺牲了它们的渲染质量;BlockNeRF本质上使用多个nerf来增加总模型容量。我们的工作不是纯粹的mlp,而是建立在TensoRF[7]中基于张量分解的特征编码上,实际上我们在降低模型容量的同时实现了卓越的渲染质量。
Sparse Tri-Vector Field Representation
我们现在提出了我们的新辐射场表示。本质上,我们的模型由多尺度的小局部三向量张量组成,旨在利用稀疏性和多尺度空间相干性(见图2)。
三向量张量云 $\mathcal{T}=\{\tau_n|n=1,…,N\}$
每个局部张量τ位于p,覆盖一个边长为l的局部立方体空间ω。这个三向量张量云代表了3D空间的辐射场: $\Omega=\bigcup_{n=1}^N\omega_n.$ Eq.1
在这里,每个张量τ编码一个局部多通道特征网格,其中包括一个(单通道)密度网格$A_{\sigma}$和一个(多通道)外观网格$A_{c}$,类似于TensoRF中的张量网格[7]。与在TensoRF中使用单个全局张量[7]相比,我们使用多个局部张量对体积密度和视图相关颜色进行建模。特别地,对于任意位置$\chi\in\Omega$,我们选择M个覆盖$χ$的最近张量。在选择的张量中,我们将提取的密度和由它们的三向量因子恢复的外观特征进行聚合,用于辐射场属性回归,其中在聚合后直接获得体积密度σ,并通过小MLP $ψ$随观察方向回归与视图相关的颜色c。连续辐射场可表示为:
$\sigma_{\chi},c_{\chi}=A_{\sigma}(\{\mathcal G^{\sigma}(\chi)\}),\psi(A_{c}(\{\mathcal G^{c}(\chi)\}),\mathbf{d}).$ Eq.2
Local tri-vector tensors.
我们应用经典的正则多进(CP)分解[5]来模拟具有三向量分量的局部张量。
CP decomposition.
CP分解将M维张量$\tau\in\mathbb{R}^{I_1\times I_2\times\ldots\times I_M}$因式分解为R个rank-1张量的线性组合:
$\tau=\sum_{r=1}^{R}\lambda_{r}\mathbf{v}_{r}^{0}\otimes\mathbf{v}_{r}^{1}\otimes…,\otimes\mathbf{v}_{r}^{M},$ Eq.3
式中⊗表示外积;权重因子$λ_{r}$可以吸收成向量$\colon\{\mathbf{v}_{r}^{0},…,\mathbf{v}_{r}^{M}\}.$。
Density and appearance tensors.
在我们建模3D辐射场的例子中,我们将几何网格$\mathcal{G}^{\sigma}\in \mathbb{R}^{I\times J\times K}$设置为3D张量。多通道外观网格$\mathcal{G}^c\in\mathbb{R}^{I\times J\times K\times P}$对应一个4D张量。第四种外观mode是较低的维度(与空间模式相比),代表发送到MLP解码器网络的特征的最终维度。
根据Eqn.3,我们通过CP分解对每个张量的特征网格$\mathcal{G}^{\sigma}$和$\mathcal{G}^{c}$进行分解:
$\mathcal{G}^\sigma=\sum_{r=1}^{R_\sigma}\mathcal{A}_{\sigma,r}=\sum_{r=1}^{R_\sigma}\mathrm{v}_{\sigma,r}^X\otimes\mathrm{v}_{\sigma,r}^Y\otimes\mathrm{v}_{\sigma,r}^Z,$ Eq.4
$\mathcal{G}^c=\sum_{r=1}^{R_c}\mathcal{A}_{c,r}\otimes\mathbf{b}_r=\sum_{r=1}^{R_c}\mathbf{v}_{c,r}^X\otimes\mathbf{v}_{c,r}^Y\otimes\mathbf{v}_{c,r}^Z\otimes\mathbf{b}_r,$ Eq.5
其中,$R_{\sigma}$和$R_{c}$表示组分数;$\mathcal{A}_{\sigma,r}$和$\mathcal{A}_{c,r}$是空间分解的分量张量;$\mathbf{V}_{\sigma,r}^{X},…,\mathbf{V}_{c,r}^{X},…$分别为分辨率为I、J、K的一维矢量,沿X、Y、z轴对场景几何形状和外观进行建模; $R_{\sigma}$和$R_{c}$为组分数;$\mathbf{b}_{r}$表示特征维度
正如在TensoRF[7]中所做的那样,我们将所有特征模式向量$\mathbf{b}_{r}$作为列堆叠在一起,最终得到$P\times R_{c}$外观矩阵B。该矩阵对张量的外观特征变化进行建模,并发挥外观字典的作用。注意,像TensoRF这样天真的CP分解将为每个局部张量分配不同的外观矩阵。相反,我们建议利用在整个局部张量云上共享的全局外观矩阵Bc,从而产生一个全局外观字典,解释整个场景的颜色相关性。这进一步提高了模型的计算效率和模型紧凑性。
因此,每个局部张量都由它们唯一的局部三向量因子$\mathbf{v}_{r}^{X},\mathbf{v}_{r}^{Y},\mathbf{v}_{r}^{Z}.$表示。
Feature evaluation.
为了获得一个连续的场,我们在评估张量网格特征时考虑了三线性插值。对于位置$χ$,我们首先计算其相对于位于$p$处的选定张量的位置$\tilde{X}$:
$\tilde{x},\tilde{y},\tilde{z}=x-p_x,y-p_y,z-p_z.$ Eq.6
然后,例如,为了得到在$(\tilde{x},\tilde{y},\tilde{z})$处的$\mathcal{A}_{\sigma,r}$ ,我们可以在角上计算并三线性插值8个$\mathcal{A}_{\sigma,r}$。
如[7]所述,首先对每个向量进行线性插值在数学上是等价的,可以减少计算成本。根据外积法则,有$\mathcal{A}_{r,i,j,k}=\mathbf{v}_{r,i}^{X}\mathbf{v}_{r,j}^{Y}\mathbf{v}_{r,k}^{Z},$则在$χ$位置插值的密度特征为:
$\mathcal{G}^{\sigma}(\chi)=\sum_{r}\mathbf{v}_{\sigma,r}^{X}(\tilde{x})\mathbf{v}_{\sigma,r}^{Y}(\tilde{y})\mathbf{v}_{\sigma,r}^{Z}(\tilde{z})=\sum_{r}\mathcal{A}_{\sigma,r}(\tilde{\chi}),$ Eq.7
其中$\mathbf{v}_{\sigma,r}^{X}(\tilde{x})$是$\mathrm{v}_{\sigma,r}^X$在x轴(x)处的线性插值值。这里,$\mathcal{G}^{\sigma}(\chi)$是一个标量。
同样,插值后的外观特征可以计算为: Eq.8,9,10
其中“⊕”表示串联concatenation,“·”表示点积。外观特征$\mathcal{G}^c(\chi)\in\mathbb{R}^P$是一个向量。
Feature aggregation.
我们建议聚合来自M个相邻张量的特征,以联合建模每个3D位置的体积密度和外观χ。特别是,受Point-NeRF的启发,我们利用基于逆距离的加权函数来直接聚合多张量特征。具体来说,这个权重可以表示为$w_m=\frac{1}{|p_m-\chi|}.$ Eq.11
有了这个权函数,我们直接通过加权和得到密度特征:
$f^{\sigma}(\chi)=\frac{1}{\sum w_{m}}\sum_{m=1}^{M}w_{m}\mathcal{G}_{m}^{\sigma}(\chi).$ Eq.12
同样,外观特征聚合也可以用类似的方式表示,同时使用跨局部张量的共享外观矩阵(如第3.1节所述): Eq.13,14,15
注意,由于在张量之间共享外观矩阵,我们将计算复杂度从Eqn.14中的$O(M\cdot P\cdot R_c)$降低到Eqn.15中的$O((M+P)\cdot R_{c})$。
Multi-scale tri-vector fields.
复杂的3D场景通常包含多频几何和外观细节。这促使我们构建多尺度张量云,以发现多尺度下的局部几何和外观共性。我们最终的亮度场是由多个三向量张量云在S不同的尺度。不同的云由不同分辨率的张量组成
为了回归位置$χ$的密度和外观,我们从覆盖$χ$的一组张量云中收集密度和外观特征,$\{\mathcal{T}_{s}|1\leq s\leq S,\chi\in\Omega_{s}\}$。请注意,某些尺度的张量云可能没有覆盖位置,因此$\mathfrak{l}|\{\mathcal{T}_{s}\}|\leq S.$。我们简单地计算这些尺度上的平均特征:
$f^{\sigma}(\chi)=\frac{1}{|\{\mathcal{T}_{s}\}|}\sum_{s}f_{s}^{\sigma}(\chi),$ Eq.16
$f^{c}(\chi)=\frac{1}{|\{\mathcal{T}_{s}\}|}\sum_{s}f_{s}^{c}(\chi).$ Eq.17
注意,$f^{\sigma}(\chi)$和$f^{c}(\chi)$是我们在多个尺度和多个相邻张量上聚合的最终密度和外观特征。
Decoding.
我们对密度特征$f^{\sigma}(\chi)$应用softplus激活来获得最终的体积密度,并通过将外观特征$f^{c}(\chi)$和观察方向d发送到MLP解码器$ψ$来回归与视图相关的颜色。
Rendering and Reconstruction
Volume Rendering
我们评估每个像素的颜色与基于物理的体积渲染通过可微分射线推进。根据NeRF[26],我们在$\{\chi_{q}\mid q=1,…,Q\}$沿射线,并按密度累积辐照度: Eq.18
$c=\sum_{q=1}^{Q}T_{q}(1-\exp(-\sigma_{q}\delta_{q}))c_{q},$
$T_{q}=\exp(-\sum_{t=1}^{q-1}\sigma_{t}\delta_{t}).$
$\sigma_q\mathrm{~and~}c_q$为遮光点的密度和亮度; $δ_{t}$为每一步的行进距离;T为透光率。
Distributing local tensors
首先,为了更好地利用场景的稀疏性,我们首先获得一个大致覆盖场景几何的几何先验。几何先验可以是任何常用的形式,例如点云、占用网格、八叉树或网格顶点。然后我们可以在几何的空间邻域中均匀分布张量。对于多尺度模型,每个尺度都是独立分布的。对于我们的大多数结果,我们快速地从多视图图像中优化一个粗糙的RGBA体积,并使用优化的占用网格作为先验几何,就像在DVGO中所做的那样[36],这在几秒钟内完成。
为了保持训练的稳定性和速度,每个张量$τ$的位置$p$和覆盖范围$ω$一旦确定就固定。我们还初始化了每个正态分布张量的$3(Rσ + Rc)$向量$(\mathbf{v}_{\sigma,r}^X,…,\mathbf{v}_{c,r}^X,…)$。对于每个尺度s, $P\times R_{c}$外观矩阵$\mathrm{B}_{s}^{c}$由该尺度的所有三向量张量共享。具体来说,Eqn.15中的“$\mathbf{B}^{c}\cdot()$”可以高效地实现为全连接神经层。因此,每个尺度的$B^{c}$和全局外观MLP $ψ$将被实现为神经网络,并通过默认方法初始化[15]。
Optimization and objectives.
给定一组具有相机姿态的多视图RGB图像,在地面真实像素颜色的监督下,对稀疏三向量辐射场进行逐场景优化以重建辐射场。根据体渲染方程18,L2渲染损失可以回溯到全局MLP和聚合特征,然后,一直到局部张量的外观矩阵和特征向量。
我们使用渲染损失来监督重建,并在密度特征向量$\mathbf{V}_{\sigma,r}$上应用L1正则化损失来提高几何稀疏性,并避免像TensoRF[7]中所做的那样过拟合:
$\mathcal{L}_r=|C-\tilde{C}|_2^2,$ Eq.19
$\mathcal{L}_{L1}=\frac{1}{N}\sum_{r}^{R_{\sigma}}|\mathbf{v}_{\sigma,r}|,$ Eq.20
式中,$\tilde{C}$为地面真值像素颜色,$|\mathbf{v}_{\sigma,r}|$为密度向量上各元素绝对值之和,N为元素总数。总损失为:
$\mathcal{L}=\mathcal{L}_{r}+\alpha\mathcal{L}_{L1}.$ Eq.21
我们将稀疏项α的权值默认设置为1e−5。
Implementation
获得粗糙的场景几何:30s内获得$100^{3}$的占据体积,如果存在可用的几何数据,我们可以跳过这一步
默认尺度数为3
在[-1,1]的场景框中,我们将场景几何(被占用的体素中心或点)栅格化到3个不同体素大小的网格上,例如$0.4^{3},0.2^{3},0.1^{3}$。对于每个网格,我们在其占用体素的中心分布三向量张量。3个尺度的张量空间覆盖度分别为$0.6^{3}、0.3^{3}、0.15^{3}$。对于每个尺度,我们查询M = 4个附近张量
据[36],我们的特征解码网络$ψ$是一个具有128个通道的2层MLP。对于每个尺度,其外观矩阵$B^{c}$由27个通道的单一线性层实现
我们在PyTorch[17]中使用自定义的CUDA操作来实现该框架。在优化过程中,我们采用[7]中的粗到细策略,将向量的维数(I, J, K)从29线性上采样到121,从15上采样到61,从7上采样到31。上采样发生在第2000、3000、4000、5500和7000步。我们使用Adam优化器[19],初始学习率为向量的0.02,网络的0.001。在单个3090 RTX GPU上,我们训练每个模型30000步,而每个批次包含4096条射线。请在补充材料中找到更多的细节。
Experiments
- Evaluation on the NeRF Synthetic Dataset.
- Evaluation on the real datasets.
- The ScanNet dataset.
- The Tanks and Temples dataset.
- Ablation study