| Title | TensoRF: Tensorial Radiance Fields |
|---|---|
| Author | Anpei Chen*, Zexiang Xu*, Andreas Geiger, Jingyi Yu, Hao Su |
| Conf/Jour | ECCV |
| Year | 2022 |
| Project | TensoRF: Tensorial Radiance Fields (apchenstu.github.io) |
| Paper | TensoRF: Tensorial Radiance Fields (readpaper.com) |
Conclusion
我们提出了一种高质量场景重建和渲染的新方法。我们提出了一种新的场景表示TensoRF,它利用张量分解技术将辐射场紧凑地建模和重建为分解的低秩张量分量。虽然我们的框架包含了经典的张量分解技术(如CP),但我们引入了一种新的向量矩阵分解VM,从而提高了重建质量和优化速度。
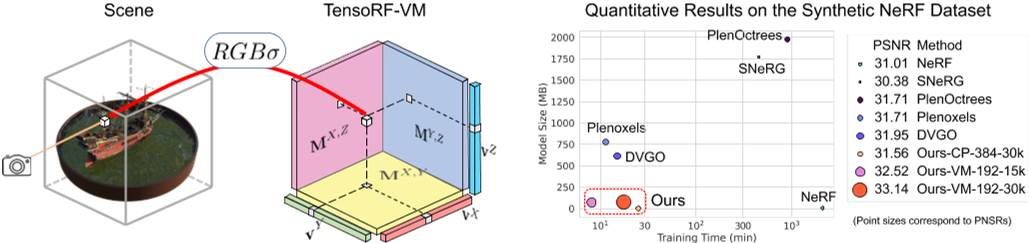
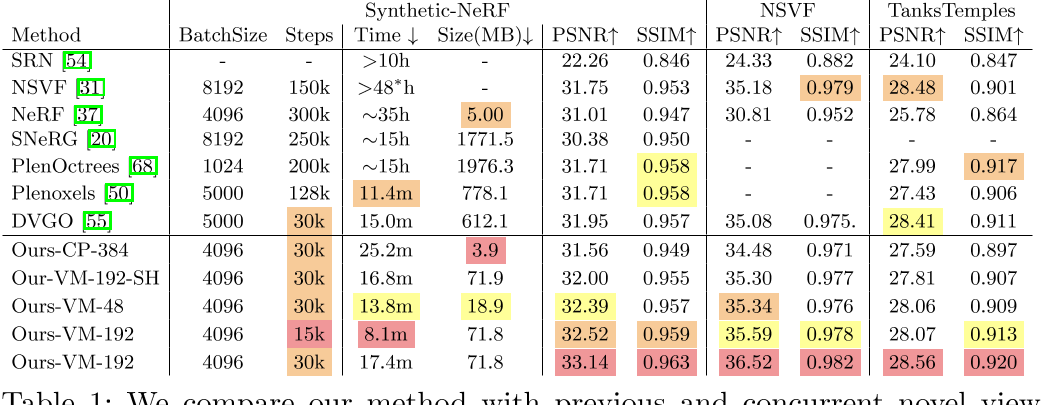
我们的方法可以在每个场景不到30分钟的时间内实现高效的辐射场重建,与需要更长的训练时间(20多个小时)的NeRF相比,可以获得更好的渲染质量。此外,我们基于张量分解的方法实现了高紧凑性,导致内存占用小于75MB,大大小于许多其他先前和并发的基于体素网格的方法。我们希望我们在张张化低秩特征建模方面的发现可以对其他建模和重建任务有所启发。
AIR
我们提出了一种新的建模和重建辐射场的方法——TensoRF。与纯粹使用mlp的NeRF不同,我们将场景的亮度场建模为4D张量,它代表具有每体素多通道特征的3D体素网格。我们的中心思想是将4D场景张量分解成多个紧凑的低秩张量分量。我们证明,在我们的框架中应用传统的CANDECOMP/PARAFAC (CP)分解-将张量分解为具有紧向量的秩一分量-可以改善vanilla NeRF。
为了进一步提高性能,我们引入了一种新的向量矩阵(VM)分解,该分解放松了张量的两种模式的低秩约束,并将张量分解为紧凑的向量和矩阵因子。除了卓越的渲染质量之外,与之前和并发的直接优化每体素特征的工作相比,我们使用CP和VM分解的模型显著降低了内存占用。实验证明,与NeRF相比,具有CP分解的TensoRF实现了快速重建(< 30分钟),具有更好的渲染质量,甚至更小的模型大小(< 4 MB)。此外,具有VM分解的TensoRF进一步提高了渲染质量,优于以前最先进的方法,同时减少了重建时间(< 10分钟)并保留了紧凑的模型大小(< 75 MB)。
Introduction
建模和重建3D场景作为支持高质量图像合成的表示对于计算机视觉和图形在视觉效果,电子商务,虚拟和增强现实以及机器人技术中的各种应用至关重要。
最近,NeRF[37]及其许多后续工作[70,31]已经成功地将场景建模为辐射场,并实现了具有高度复杂几何和视图依赖外观效果的场景的逼真渲染。尽管(纯粹基于mlp的)NeRF模型需要很小的内存,但它们需要很长时间(数小时或数天)来训练。在这项工作中,我们追求一种新颖的方法,既有效的训练时间和紧凑的内存占用,同时达到最先进的渲染质量。
为了做到这一点,我们提出了TensoRF,这是一种新颖的亮度场表示,它非常紧凑,也可以快速重建,实现高效的场景重建和建模。与NeRF中使用的基于坐标的mlp不同,我们将亮度场表示为显式的特征体素网格。
需要注意的是,目前尚不清楚体素网格表示是否能提高重建的效率: 虽然之前的工作使用了特征网格[31,68,20],但它们需要较大的GPU内存来存储尺寸随分辨率呈立方增长的体素,有些甚至需要预先计算NeRF进行蒸馏,导致重建时间很长。
我们的工作在一个原则框架中解决了体素网格表示的低效率问题,从而产生了一系列简单而有效的方法。我们利用了一个事实,即特征网格可以自然地被视为一个4D张量,其中三个模式对应于网格的XYZ轴,第四个模式代表特征通道维度。这开启了利用经典张量分解技术进行辐射场建模的可能性,该技术已广泛应用于各个领域的高维数据分析和压缩[27]。因此,我们建议将亮度场张量分解为多个低阶张量分量,从而获得准确而紧凑的场景表示。注意,我们的中心思想张量化辐射场是一般的,可以潜在地采用任何张量分解技术。
在这项工作中,我们首先尝试了经典的CANDECOMP/PARAFAC (CP)分解[7]。我们表明,使用CP分解的TensoRF已经可以实现逼真的渲染,并产生比纯粹基于MLP的NeRF更紧凑的模型(见图1和表1)。然而,在实验中,为了进一步提高复杂场景的重建质量,我们必须使用更多的组件因子,这增加了训练时间。
因此,我们提出了一种新的向量矩阵(VM)分解技术,该技术有效地减少了相同表达能力所需的组件数量,从而实现更快的重建和更好的渲染。特别是,受CP和分块项分解[13]的启发,我们提出将辐射场的全张量分解为每个张量分量的多个矢量和矩阵因子。与CP分解中纯向量外积的和不同,我们考虑向量-矩阵外积的和(见图2)。实质上,我们通过在一个矩阵因子中联合建模两个模态来放松每个分量的两个模态的秩。虽然与CP中纯粹的基于向量的分解相比,这增加了模型的大小,但我们使每个分量能够表达更高阶的更复杂的张量数据,从而显着减少了辐射场建模所需的分量数量。
通过CP/VM分解,我们的方法紧凑地编码了体素网格中空间变化的特征。可以从特征中解码出体积密度和依赖于视图的颜色,支持体积亮度场渲染。因为张量表示离散数据,我们还启用了高效的三线性插值来表示连续场。我们的表示支持具有不同解码函数的各种类型的每体素特征,包括神经特征(依赖于MLP从特征中回归与视图相关的颜色)和球面谐波(SH)特征(系数)——允许从固定的SH函数进行简单的颜色计算,并导致没有神经网络的表示。
我们的张量辐射场可以有效地从多视图图像中重建,并实现现实的新视图合成。与之前直接重建体素的工作相比,我们的张量因式分解将空间复杂度从$\mathcal{O}(n^3)$降低到$\mathcal{O}(n)$(CP)或$\mathcal{O}(n^2)$ (VM),显著降低内存占用。请注意,虽然我们利用了张量分解,但我们不是在解决分解/压缩问题,而是基于梯度体面的重建问题,因为特征网格/张量是未知的。从本质上讲,我们的CP/VM分解在优化中提供了低秩正则化,从而获得了高渲染质量。我们通过各种设置对我们的方法进行了广泛的评估,包括CP和VM模型、不同数量的组件和网格分辨率。我们证明,所有模型都能够实现逼真的新颖视图合成结果,与之前最先进的方法相当或更好(见图1和表1)。更重要的是,我们的方法具有较高的计算和内存效率。所有TensoRF模型都能在30分钟内重建高质量的辐射场;我们最快的虚拟机分解模型需要不到10分钟,这比NeRF和许多其他方法要快得多(约100倍),同时比以前的基于体素的并行方法需要更少的内存。请注意,与需要独特数据结构和定制CUDA内核的并发工作[50,38]不同,我们的模型的效率收益是使用标准PyTorch实现获得的。据我们所知,我们的工作是第一次从张量的角度来看待辐射场建模,并将辐射场重建问题作为低秩张量重建问题之一。
Related Work
Tensor decomposition.
张量分解[27]已经研究了几十年,在视觉、图形学、机器学习和其他领域有不同的应用[43,24,59,14,1,23]。一般来说,应用最广泛的分解是Tucker分解[58]和CP分解[7,19],这两种分解都可以看作是矩阵奇异值分解(SVD)的推广。CP分解也可以看作是一种特殊的Tucker分解,其核心张量是对角的。通过将CP和Tucker分解相结合,提出了块项分解(block term decomposition, BTD)及其多种变体[13],并将其用于许多视觉和学习任务[2,67,66]。在这项工作中,我们利用张量分解进行辐射场建模。我们直接应用了CP分解,并引入了一种新的向量矩阵分解,它可以看作是一种特殊的BTD。
Scene representations and radiance fields.
各种场景表示,包括网格[18,61]、点云[47]、体[22,48]、隐式函数[35,46],近年来得到了广泛的研究。许多神经表示[10,71,53,33,4]被提出用于高质量的渲染或自然信号表示[52,56,29]。NeRF[37]引入了辐射场来解决新的视图合成并实现照片逼真的质量。这种表示已迅速扩展并应用于各种图形和视觉应用,包括生成模型[9,40]、外观获取[3,5]、表面重建[62,42]、快速渲染[49,68,20,17]、外观编辑[64,32]、动态捕获[28,44]和生成模型[41,8]。虽然导致逼真的渲染和紧凑的模型,但NeRF的纯基于mlp的表示在缓慢的重建和渲染方面存在已知的局限性。最近的方法[68,31,20]利用了辐射场建模中的特征体素网格,实现了快速渲染。然而,这些基于网格的方法仍然需要较长的重建时间,甚至导致较高的内存成本,牺牲了NeRF的紧凑性。基于特征网格,我们提出了一种新的张量场景表示,利用张量分解技术,实现快速重建和紧凑建模。
其他方法设计了跨场景训练的可通用网络模块,以实现依赖图像的亮度场渲染[57,69,63,12]和快速重建[11,65]。我们的方法侧重于亮度场表示,只考虑每个场景的优化(如NeRF)。我们表明,我们的表示已经可以导致高效率的辐射场重建,而无需任何跨场景泛化。我们把扩展留给一般化的设置作为将来的工作。
Concurrent work
在过去的几个月里,辐射场建模领域的发展非常快,许多并行的作品已经出现在arXiv上作为预印本。DVGO[55]和Plenoxels[50]还优化了(神经或SH)特征的体素网格,以实现快速辐射场重建。然而,它们仍然像以前基于体素的方法一样直接优化每体素特征,因此需要大的内存。我们的方法将特征网格分解为紧凑的组件,从而显著提高了内存效率。Instant-NGP[38]使用多分辨率哈希来实现高效编码,并导致高紧凑性。该技术与我们基于因子分解的技术是正交的; 潜在地,我们的每个向量/矩阵因子都可以用这种散列技术进行编码,我们将这种组合留到未来的工作中。EG3D[8]使用三平面表示3D gan;它们的表示类似于我们的VM分解,可以看作是具有常量向量的特殊VM版本。
CP and VM Decomposition
我们将亮度场分解成紧凑的组件用于场景建模。为此,我们应用了经典的CP分解和新的向量矩阵(VM)分解; 两者如图2所示。我们现在用一个3D(3阶)张量的例子来讨论这两种分解。我们将介绍如何在辐射场建模中应用张量因式分解(与4D张量)在第4节。

张量分解。左:CP分解(Eqn. 1),它将张量分解为向量外积的和。右:我们的向量矩阵分解(Eqn. 3),它将张量分解为向量矩阵外积的和。
CP decomposition
给定一个三维张量$\mathcal{T}\in\mathbb{R}^{I\times J\times K}$,CP分解将其分解为向量的外积和(如图2所示):
$\mathcal{T}=\sum_{r=1}^R\mathbf{v}_r^1\circ\mathbf{v}_r^2\circ\mathbf{v}_r^3$ Eq.1
其中$\mathbf{v}_r^1\circ\mathbf{v}_r^2\circ\mathbf{v}_r^3$对应一个rank-one张量分量,$\mathbf{v}_r^1\in\mathbb{R}^I$,$\mathbf{v}_r^2\in\mathbb{R}^{\boldsymbol{J}}$, $\mathbf{v}_r^3\in\mathbb{R}^K$是第r个分量三种模态的因式分解向量。上标表示每个因子的模态;◦表示外积。因此,每个张量元素$T_{ijk}$是标量积的和: $\mathcal{T}_{ijk}=\sum_{r=1}^R\mathbf{v}_{r,i}^1\mathbf{v}_{r,j}^2\mathbf{v}_{r,k}^3$ Eq.2
其中i j k表示三种模态的indices。
CP分解将一个张量分解为多个向量,表示多个紧化秩一分量。CP可以直接应用于我们的张量辐射场建模,得到高质量的结果(见表1)。但是,由于CP分解的紧凑性太高,需要很多组件来建模复杂场景,导致辐射场重构的计算成本很高。受块项分解(BTD)的启发,我们提出了一种新的VM分解方法,从而更有效地重建辐射场。
Vector-Matrix (VM) decomposition
与利用纯矢量因子的CP分解不同,VM分解将一个张量分解为多个矢量和矩阵,如图2所示。它表示为
$\mathcal{T}=\sum_{r=1}^{R_1}\mathrm{v}_r^1\circ\mathrm{M}_r^{2,3}+\sum_{r=1}^{R_2}\mathrm{v}_r^2\circ\mathrm{M}_r^{1,3}+\sum_{r=1}^{R_3}\mathrm{v}_r^3\circ\mathrm{M}_r^{1,2}$Eq.3
$\begin{aligned}\mathrm{M}_{r}^{2,3}\in\mathbb{R}^{J\times K},\mathrm{M}_{r}^{1,3}\in\mathbb{R}^{I\times K},\mathrm{M}_{r}^{1,2}\in\mathbb{R}^{I\times J}\end{aligned}$是三种模态中两个(用上标表示)的矩阵因子。对于每个组件,我们将其两个模态秩放宽为任意大,同时将第三个模态限制为秩一; 例如,对于分量张量$\mathbf{v}_{r}^{1}\circ\mathbf{M}_{r}^{2,3}$,其模1秩为1,模2和模3秩可以是任意的,这取决于矩阵$\mathrm{M}_{r}^{2,3}$的秩。一般来说,在CP中,我们不是使用单独的向量,而是将每两个模态结合起来并用矩阵表示它们,允许每个模态用较少的分量充分参数化。R1、R2、R3可设置不同,应根据每种模式的复杂程度进行选择。我们的VM分解可以看作是一般BTD的一个特例。
注意,每个分量张量都比CP分解中的分量有更多的参数。虽然这会导致较低的紧凑性,但VM分量张量可以表达比CP分量更复杂的高维数据,从而减少了对相同复杂函数建模时所需的分量数量。另一方面,与密集网格表示相比,VM分解仍然具有非常高的紧凑性,将内存复杂度从$\mathcal{O}(N^3)$降低到$\mathcal{O}(N^2)$。
Tensor for scene modeling.
在这项工作中,我们的重点是建模和重建辐射场的任务。在这种情况下,三个张量模式对应于XYZ轴,因此我们直接用XYZ表示模式以使其直观。同时,在3D场景表示中,我们对大多数场景考虑$R_{1}=R_{2}=R_{3}=R$,这反映了一个场景可以沿着它的三个轴分布和呈现同样复杂的事实。因此,Eqn. 3可以改写为
$\mathcal{T}=\sum_{r=1}^R\mathbf{v}_r^X\circ\mathbf{M}_r^{Y,Z}+\mathbf{v}_r^Y\circ\mathbf{M}_r^{X,Z}+\mathbf{v}_r^Z\circ\mathbf{M}_r^{X,Y}$ Eq.4
此外,为了简化符号和后面章节的讨论,我们还将三种类型的分量张量表示为$\mathcal{A}_r^X=\mathbf{v}_r^X\circ\mathbf{M}_r^{YZ},$$\mathcal{A}_r^Y=\mathrm{v}_r^Y\circ\mathrm{M}_r^{XZ},\mathrm{~and~}\mathcal{A}_r^Z=\mathrm{v}_r^Z\circ\mathrm{M}_r^{XY}$这里A的上标XYZ表示不同类型的组件。据此,张量元素$T_{ijk}$表示为
$\mathcal{T}_{ijk}=\sum_{r=1}^R\sum_m\mathcal{A}_{r,ijk}^m$ Eq.5
其中$m\in XYZ,\mathcal{A}_{r,ijk}^X=\mathrm{v}_{r,i}^X\mathrm{M}_{r,jk}^{YZ},\mathcal{A}_{r,ijk}^Y=\mathrm{v}_{r,j}^Y\mathrm{M}_{r,ik}^{XZ},\mathrm{~and~}\mathcal{A}_{r,ijk}^Z=\mathrm{v}_{r,k}^Z\mathrm{M}_{r,ij}^{XY}.$同样,我们也可以将CP分量表示为$\mathcal{A}^\gamma=\mathbf{v}_r^X\circ\mathbf{v}_r^Y\circ\mathbf{v}_r^Z,$并且Eqn. 5也可以通过考虑$\begin{aligned}m=\gamma,\end{aligned}$来表示CP分解,其中m的求和可以去掉。
Tensorial Radiance Field Representation
我们现在提出了张量辐射场表示(TensoRF)。为简单起见,我们专注于用我们的VM分解来表示TensoRF。CP分解较为简单,其分解方程只需稍加修改即可直接应用(如Eqn. 5)。
Feature grids and radiance field.
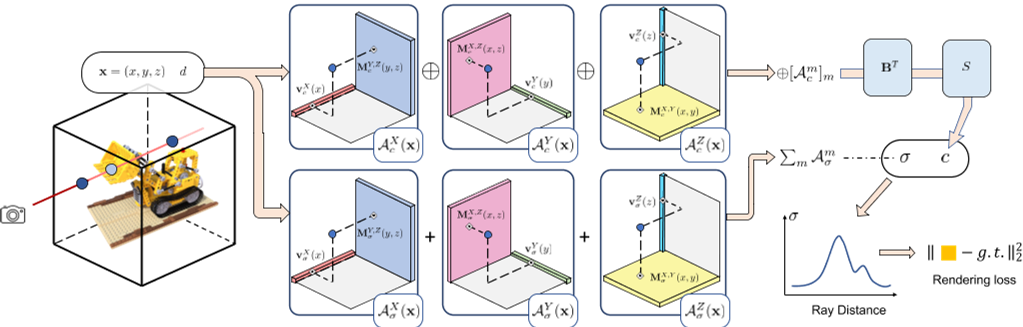
我们的目标是建模一个辐射场,它本质上是一个将任何3D位置x和观看方向d映射到其体积密度σ和视图相关颜色c的函数,支持可微分的射线行进进行体渲染。我们利用具有每体素多通道特征的常规3D网格$\mathcal{G}$来建模这样的函数。我们(通过特征通道)将其分成几何网格$\mathcal{G}_{\sigma}$和外观网格,分别对体积密度σ和视图相关颜色c进行建模。
我们的方法支持$\mathcal{G}_{c}$中的各种类型的外观特征,这取决于预先选择的函数S,它将外观特征向量和观看方向d转换为颜色c。例如,S可以是一个小的MLP或球面谐波(SH)函数,其中$\mathcal{G}_{c}$分别包含神经特征和SH系数。我们证明MLP和SH函数在我们的模型中都能很好地工作(见表1)。另一方面,我们考虑单通道网格$\mathcal{G}_{\sigma},$其值直接表示体积密度,不需要额外的转换函数。连续的基于网格的辐射场可以写成
$\sigma,c=\mathcal{G}_\sigma(\mathrm{x}),S(\mathcal{G}_c(\mathrm{x}),d)$ Eq.6
其中,$\mathcal{G}_{\sigma}$,$\mathcal{G}_{c}$表示来自位置x的两个网格的三线性插值特征。我们将$\mathcal{G}_{\sigma}$和$\mathcal{G}_{c}$建模为因式张量。
Factorizing radiance fields
$\mathcal{G}_\sigma\in\mathbb{R}^{I\times J\times K}$是三维张量,$\mathcal{G}_c\in\mathbb{R}^{I\times J\times K\times P}$是4D张量。其中I、J、K分别代表特征网格在X、Y、Z轴上的分辨率,p代表外观特征通道的个数。
我们将这些辐射场张量分解为紧化分量。特别是使用VM分解。将三维几何张量$\mathcal{G}_{\sigma}$分解为
$\mathcal{G}_\sigma=\sum_{r=1}^{R_\sigma}\mathrm{v}_{\sigma,r}^X\circ\mathrm{M}_{\sigma,r}^{YZ}+\mathrm{v}_{\sigma,r}^Y\circ\mathrm{M}_{\sigma,r}^{XZ}+\mathrm{v}_{\sigma,r}^Z\circ\mathrm{M}_{\sigma,r}^{XY}=\sum_{r=1}^{R_\sigma}\sum_{m\in XYZ}A_{\sigma,r}^m$ Eq.7
外观张量$\mathcal{G}_{c}$具有与特征通道维度相对应的附加模式。请注意,与XYZ模式相比,此模式通常具有较低的维度,从而导致较低的排名。因此,我们不将该模态与其他模态结合在矩阵因子中,而是在分解中仅使用向量$\mathbf{b}_{r}$表示该模态。具体地说,$\mathcal{G}_{c}$被分解为Eq.8
注意,我们有$3R_{c}$向量$\mathbf{b}_{r}$来匹配分量的总数。
总的来说,我们将整个张量辐射场分解为$3R_{\sigma}+3R_{c}$矩阵$(\mathbf{M}_{\sigma,r}^{YZ},…,\mathbf{M}_{c,r}^{YZ},…)$和$3R_{\sigma}+6R_{c}$向量$(\mathbf{v}_{\sigma,r}^{X},…,\mathbf{v}_{c,r}^{X},…,\mathbf{b}_{r}).$。一般而言,我们采用$R_{\sigma}\ll I,J,K$, $R_{c}\ll I,J,K$,从而形成高度紧凑的表示,可以对高分辨率的密集网格进行编码。本质上,xyz模向量和矩阵因子,$\mathbf{v}_{\sigma,r}^{X},\mathbf{M}_{\sigma,r}^{YZ},\mathbf{v}_{c,r}^{X},\mathbf{M}_{c,r}^{YZ},…,$描述场景几何和外观沿其相应轴的空间分布。另一方面,外观特征模态向量$\mathbf{b}_{r}$表示全局外观相关性。通过将所有$\mathbf{b}_{r}$作为列叠加在一起,我们得到一个$P\times3R_{c}$矩阵B; 这个矩阵B也可以被视为一个全局外观字典,它抽象了整个场景的外观共性。
Efficient feature evaluation.
我们基于因子分解的模型可以以低成本计算每个体素的特征向量,每个xyz模式向量/矩阵因子只需要一个值。我们还为我们的模型启用了有效的三线性插值,从而导致连续场。
Direct evaluation.
通过VM分解,单个体素在指标ijk处的密度值$\mathcal{G}_{\sigma,ijk}$可以通过公式5直接有效地求出:
$\mathcal{G}_{\sigma,ijk}=\sum_{r=1}^{R_\sigma}\sum_{m\in XYZ}\mathcal{A}_{\sigma,r,ijk}^{m}$ Eq.9
在这里,计算每个$\mathcal{A}_{\sigma,r,ijk}^m$只需要索引和乘以对应向量和矩阵因子的两个值。
对于外观网格$\mathcal{G}_{c}$,我们总是需要计算一个完整的P通道特征向量,着色函数S需要作为输入,对应于固定XYZ索引ijk的$\mathcal{G}_{c}$的1D切片:
$\mathcal{G}_{c,ijk}=\sum_{r=1}^{R_{c}}\mathcal{A}_{c,r,ijk}^X\mathbf{b}_{3r-2}+\mathcal{A}_{c,r,ijk}^Y\mathbf{b}_{3r-1}+\mathcal{A}_{c,r,ijk}^Z\mathbf{b}_{3r}$ Eq.10
在这里,特征模式没有额外的索引,因为我们计算了一个完整的向量。我们通过重新排序计算进一步简化Eqn. 10。为此,我们将$\oplus[\mathcal{A}_{c,ijk}^m]_{m,r}$表示为叠加$m=X,Y,Z$和 $r=1,…,R_{c}$所有$\mathcal{A}_{c,r,ijk}^{m}$值的向量,它是一个$3R_{c}$维的向量;在实践中,⊕也可以被看作是将所有标量值(1通道向量)连接成$3R_{c}$通道向量的连接运算符。使用矩阵B(在4.1节中介绍)堆叠所有的$\mathbf{b}_{r}$, Eqn. 10等价于矩阵向量积: $\mathcal{G}_{c,ijk}=\mathbf{B}(\oplus[\mathcal{A}_{c,ijk}^m]_{m,r})$ Eq.11
注意,公式11不仅在形式上更简单,而且在实践中也导致了更简单的实现。具体来说,当并行计算大量体素时,我们首先计算并连接所有体素的$\mathcal{A}_{c,r,ijk}^{m}$作为矩阵中的列向量,然后将共享矩阵B乘以一次。
Trilinear interpolation.
我们用三线性插值法对连续场进行建模。Na ively实现三线性插值是昂贵的,因为它需要评估8个张量值并对它们进行插值,与计算单个张量元素相比,计算量增加了8倍。然而,我们发现,由于三线性插值和外积的线性之美,对分量张量的三线性插值自然等同于对相应模态的向量/矩阵因子的线性/双线性插值。
例如,给定一个分量张量$\mathcal{A}_{r}^{X}=\mathrm{v}_{r}^{X}\circ\mathrm{M}_{r}^{YZ}$及其每个张量元素$\mathcal{A}_{r,ijk}=\mathrm{v}_{r,i}^{X}\mathrm{M}_{r,jk}^{YZ},$,我们可以计算其插值值为: $\mathcal{A}_r^X(\mathrm{x})=\mathrm{v}_r^X(x)\mathrm{M}_r^{YZ}(y,z)$ Eq.12
其中$\mathcal{A}_r^X(\mathrm{x})$是$\mathcal{A}_r$在三维空间中位置x = (x, y, z)处的三线性插值值,$\mathrm{v}_{r}^{X}(x)$是$\mathrm{v}_{r}^{X}$在x轴上在x处的线性插值值,$\mathrm{M}_{r}^{YZ}(y,z)$是$\mathrm{M}_{r}^{YZ}$在YZ平面上在(y, z)处的二线性插值值。类似地,我们有$\mathcal{A}_{r}^{Y}(\mathbf{x})=\mathbf{v}_{r}^{Y}(y)\mathbf{M}_{r}^{XZ}(x,z)$和$\mathcal{A}_{r}^{Z}(\mathbf{x})=\mathbf{v}_{r}^{Z}(z)\mathbf{M}_{r}^{XY}(x,y)$(对于CP分解,$\mathcal{A}_{r}^{\gamma}(\mathbf{x})=\mathbf{v}_{r}^{X}(x)\mathbf{v}_{r}^{Y}(y)\mathbf{v}_{r}^{Z}(z)$也是有效的)。因此,对两个网格进行三线性插值表示为
$\mathcal{G}_\sigma(\mathrm{x})=\sum_r\sum_m\mathcal{A}_{\sigma,r}^m(\mathrm{x})$ Eq.13
$\mathcal{G}_c(\mathrm{x})=\mathbf{B}(\oplus[\mathcal{A}_{c,r}^m(\mathrm{x})]_{m,r})$ Eq.14
这些方程与公式9和11非常相似,只是用插值值替换张量元素。我们避免了恢复8个单独的张量元素进行三线性插值,而是直接恢复插值值,从而降低了运行时的计算和内存成本。
Rendering and reconstruction.
方程6,12 - 14描述了我们模型的核心组成部分。结合公式6、13、14,分解后的张量辐射场可表示为
$\sigma,c=\sum_{r}\sum_{m}\mathcal{A}_{\sigma,r}^{m}(\mathrm{x}),S(\mathbf{B}(\oplus[\mathcal{A}_{c,r}^{m}(\mathrm{x})]_{m,r}),d)$ Eq.15
也就是说,在给定任何3D位置和观看方向的情况下,我们获得连续的体积密度和与视图相关的颜色。这允许高质量的辐射场重建和渲染。请注意,这个方程是通用的,并且描述了具有CP和VM分解的TensoRF。我们的辐射场重建和VM分解渲染的完整管道如图3所示。
Volume rendering.
为了渲染图像,我们使用可微体渲染,遵循NeRF[37]。具体来说,对于每个像素,我们沿着一条射线前进,沿着射线采样q个阴影点并计算像素颜色
$C=\sum_{q=1}^Q\tau_q(1-\exp(-\sigma_q\Delta_q))c_q,\tau_q=\exp(-\sum_{p=1}^{q-1}\sigma_p\Delta_p)$ Eq.16
其中,$\sigma_q,c_q$是我们的模型在它们的采样位置$\mathbf{x}_{q}$计算出的相应的密度和颜色;$\Delta_{q}$为射线步长,$τ_{q}$为透射率。
Reconstruction.
给定一组具有已知相机姿势的多视图输入图像,我们的张量辐射场通过梯度下降来优化每个场景,最小化L2渲染损失,仅使用地面真实像素颜色作为监督。
我们的辐射场由张量分解解释,并由一组全局向量和矩阵建模,作为优化中整个场的关联和正则化的基本因素。然而,这有时会导致梯度下降中的过拟合和局部最小问题,导致观测值较少的区域出现异常值或噪声。我们利用压缩感知中常用的标准正则化术语,包括向量和矩阵因子上的L1范数损失和TV(总变化)损失,有效地解决了这些问题。我们发现仅应用L1稀疏性损失对于大多数数据集是足够的。然而,对于输入图像很少的真实数据集(如LLFF[36])或不完美的捕获条件(如坦克和寺庙[26,31],具有不同的曝光和不一致的掩模),TV损失比L1范数损失更有效。
为了进一步提高质量和避免局部极小值,我们应用粗到细重建。不像以前的粗到细技术,需要对其稀疏选择的体素集进行独特的细分,我们的粗到细重建只是通过线性和双线性上采样我们的xyz模式向量和矩阵因子来实现。
Implementation details
特征接码函数S : MLP或SH函数,P=27个特征
- SH:对应于具有RGB通道的三阶SH系数
- Neural Features:使用带有两个FC层(128通道隐藏层)和ReLU激活的小型MLP
Adam优化
- 张量因子lr = 0.02
- MLP解码器lr = 0.001
GPU:Tesla V100 16GB
Experiments
提出了一个广泛的评估我们的张量辐射场。我们首先分析分解技术、组件数量、网格分辨率和优化步骤。然后,我们将我们的方法与之前和并发的360度对象和面向数据集的工作进行比较。
- Analysis of different TensoRF models.
- Optimization steps
- Comparisons on 360◦ scenes
- Forward-facing scenes