| Title | Tri-MipRF: Tri-Mip Representation for Efficient Anti-Aliasing Neural Radiance Fields |
|---|---|
| Author | Wenbo Hu Yuling Wang |
| Conf/Jour | ICCV |
| Year | 2023 |
| Project | Tri-MipRF: Tri-Mip Representation for Efficient Anti-Aliasing Neural Radiance Fields (wbhu.github.io) |
| Paper | Tri-MipRF: Tri-Mip Representation for Efficient Anti-Aliasing Neural Radiance Fields (readpaper.com) |
2023.7.26 SOTA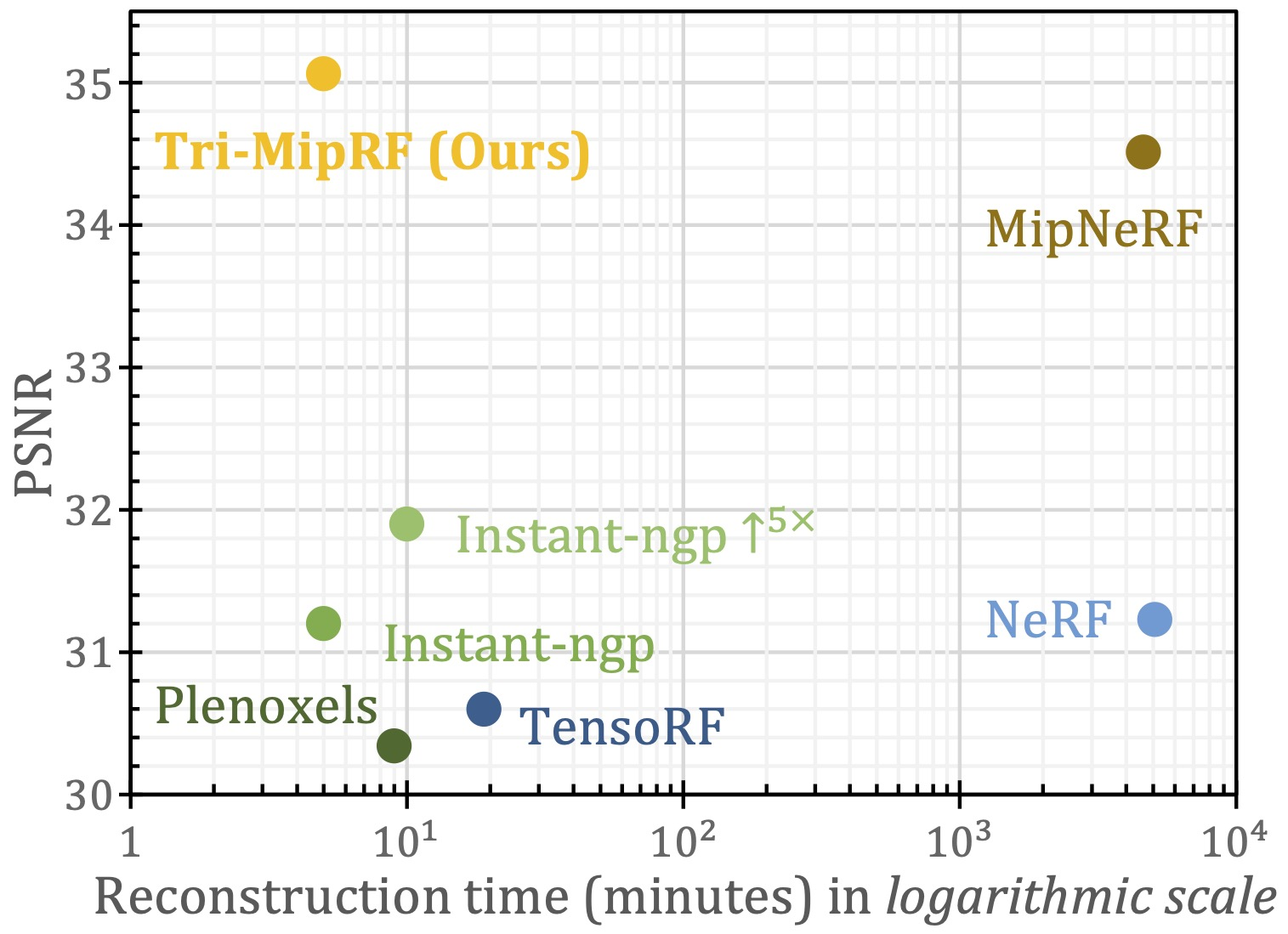
like TensoRF: Tensorial Radiance Fields (apchenstu.github.io)+ Mip-NeRF + NGP
类似Mip-NeRF中的采样锥形方法,但是Tri-MipRF使用了与圆锥相切的采样球S=(x,r),代替Mip-NeRF中的多元高斯圆锥体
- 采样球的半径通过像素圆盘半径$\dot r$(由像素大小in world Coordinate),焦距f和$t_i$确定
类似TensoRF中的分解方法,将空间采样球分解到三个平面上,编码类似NGP中的HashGrid 使用2D平面来存取特征值,构建一个base level:$M^{L_{0}}$,通过downscaling来获得其他level的2D grid平面。
- 通过base level中interest space的AABB求出$\ddot r$,并联合采样球半径r得到采样球在平面投影的level,根据此level和投影到平面上的二维坐标,在相邻两level $\mathcal{M}_{XY}^{\lfloor l\rfloor}$和$\mathcal{M}_{XY}^{\lceil l\rceil}$的2D grid中采用3线性插值得到采样球的特征值,最后三个分解平面的特征值cat起来作为MLP的一个输入
一种更好的渲染视图方法:Hybrid Volume-Surface Rendering
- 通过在密度场中marching cubes和网格抽取来获得代理网格,粗略确定相机原点到物体表面的距离
- 对代理网格进行有效栅格化,以获得圆锥体中轴线表面上的命中点,然后我们在距圆锥体中轴线命中点∆t距离内均匀采样球体,这产生2∆t采样间隔。
- 优点:可以减少需要采样点的数量,且不会影响渲染出来图片的质量
优点:
- fine-grained details in close-up views
- and free of aliasing in distant views
- 5 minute and smaller model parameters
缺点:
- 需要使用multi-view segmentation methods将In-the-wildIn数据集中感兴趣的物体提取出来
- 即需要mask
- 需要使用multi-view segmentation methods将In-the-wildIn数据集中感兴趣的物体提取出来
Conclusion
In this work, we propose a Tri-Mip radiance fields, TriMipRF, to make the renderings contain
- fine-grained details in close-up views
- and free of aliasing in distant views while maintaining efficient reconstruction, i.e. within five minutes, and compact representation, i.e. 25% smaller model size than Instant-ngp.
- This is realized by our novel Tri-Mip encoding and cone casting.
- The Tri-Mip encoding featurizes the 3D space by three mipmaps to model the pre-filtered 3D feature space, such that the sample spheres from the cone casting can be encoded in an area-sampling manner.
We also develop a hybrid volume-surface rendering strategy to enable real-time rendering (> 60 FPS) on consumer-level devices.
Extensive quantitative and qualitative experiments demonstrate our Tri-MipRF achieves state-of-the-art rendering quality while having a super-fast reconstruction speed. Also, the reconstruction results on the in-the-wild captures demonstrate the applicability of our Tri-MipRF.
AIR
- MipNeRF[3]呈现了精细的和抗锯齿渲染,但需要几天的训练
- Instant-ngp[37]可以在几分钟内完成重建,但由于忽略采样区域,在不同距离或分辨率下渲染时存在模糊或混像
为此,我们提出了一种新颖的Tri-Mip encoding(“mipmap”),可以实现神经辐射场的即时重建和抗混叠高保真渲染
- 将预滤波的三维特征空间分解成三个正交的mipmap,通过这种方式,我们可以利用2D预滤波特征图高效地进行3D区域采样,在不牺牲效率的情况下显著提高了渲染质量。为了处理新颖的Tri-Mip表示,我们提出了一种锥形渲染技术,在考虑像素成像和观察距离的情况下,使用Tri-Mip编码有效地采样抗锯齿3D特征。
Introduction
- NeRF: MLP进行训练隐式模型
- MipNeRF通过集成位置编码对预过滤的亮度场进行建模,进一步突破了渲染质量的界限。然而,如此令人印象深刻的视觉质量,在重建和渲染阶段都需要昂贵的计算,例如,MipNeRF[3]需要三天以上的重建时间,渲染一帧需要几分钟。
- InstantNGP另一方面,最近的研究提出了显式或混合表示来实现高效渲染[43,17,56,20,10,6]或重构[14,47,9,37],例如哈希编码[37]将重构时间从几天大大缩短到几分钟,实现了实时渲染。但是他们的渲染模型在基于点的采样上都存在缺陷,导致近景渲染过于模糊,远景渲染过度混叠。
- 由于缺乏支持有效区域采样的表示,我们面临着质量和效率之间权衡的困境。
在本文中,我们的目标是设计一个既支持高保真抗混叠渲染又支持高效重建的RF(radiance field)表示。为了解决混叠和模糊问题,
超采样
- 离线
- 通过对每个像素的足迹进行多重光线的超采样会大大增加计算成本
预滤波(又称区域采样), NGP中的占据网格,只对感兴趣的区域进行采样
- 实时渲染
- 直接对3D体积进行预滤波也会占用大量内存和计算量,这与效率的目标相冲突
- 由于哈希冲突,预过滤用哈希编码表示的亮度字段也不是很简单
我们通过新颖的Tri-Mip辐射场(Tri-MipRF)实现了这一具有挑战性的目标。如图1所示,我们的Tri-MipRF实现了最先进的渲染质量,在特写视图中呈现高保真细节,并且在远处视图中没有混叠。同时,它可以超快地重建,即在单个GPU上5分钟内,而哈希编码的超采样变体Instant-ngp 5x需要大约10分钟的重建时间,并且渲染质量要低得多。
通过三个2D mip (multum in parvoto)地图来呈现3D空间。Tri-Mip编码首先将3D空间分解为三个平面(planeXY, planeXZ和planeY Z),灵感来自于[PDF] Efficient Geometry-aware 3D Generative Adversarial Networks-论文阅读讨论-ReadPaper中3D内容生成的分解,然后用一个mipmap表示每个平面。
它巧妙地利用二维mipmaps的不同层次对预滤波的三维特征空间进行建模。我们的Tri-MipRF属于混合表示,因为它通过Tri-Mip编码和一个微小的MLP来建模辐射场,这使得它在重建过程中收敛得很快。我们的方法的模型大小相对紧凑,因为MLP非常浅,而Tri-Mip编码只需要三个2D地图来存储mipmap的base level。
为了处理Tri-Mip编码,我们提出了一种有效的锥形投射渲染技术,该技术将像素作为一个圆盘,并为每个像素发出一个锥形。与MipNeRF用多元高斯对圆锥体进行采样不同,我们采用圆锥体内切的球体。球体根据其占用的面积进一步以Tri-Mip编码为特征。这样做的原因是mipmaps中的特征是各向同性预过滤的。Tri-MipRF编码对预滤波后的三维特征空间进行建模,锥形投射自适应渲染距离和分辨率,它们通过采样球的占用面积有效地连接在一起,使我们的Tri-MipRF渲染结果在近距离视图中没有模糊,在远距离视图中没有混叠。此外,我们还开发了一种混合体面渲染策略,以便在消费级gpu上实现实时渲染,例如在Nvidia RTX 3060显卡上实现60 FPS。
我们在公共基准和野外拍摄的图像上广泛评估了我们的Tri-MipRF。定量和定性结果均证明了该方法在高保真渲染和快速重建方面的有效性。我们的贡献总结如下
- 我们提出了一种新颖的Tri-Mip编码,通过利用多级2D mipmaps对预滤波的3D特征空间进行建模,从而通过有效的区域采样实现抗混叠体渲染。
- 我们提出了一种新的锥体投射渲染技术,该技术可以有效地为每个像素发出一个锥体,同时在Tri-Mip编码的3D空间上优雅地用球体对锥体进行采样
- 我们的方法实现了最先进的渲染质量和重建速度(在单个GPU上5分钟内),同时仍然保持了紧凑的表示(模型尺寸比Instantngp小25%)。由于混合体面渲染策略,我们的方法在部署在消费者级设备上时也实现了实时渲染。
Related Work
Anti-aliasing in rendering.抗混叠是计算机图形学和图像处理中的一个基本问题,在渲染界得到了广泛的研究。从数学上讲,混叠是采样率不足导致频率分量重叠的结果。超采样和预滤波(区域采样)分别是离线和实时渲染算法中减少混叠的两种典型方法。超采样抗混叠(Super-sampling anti-aliasing, SSAA)方法[15,11,32,19,51]直接提高采样率以接近奈奎斯特频率,而多采样抗混叠(multi-sampling anti-aliasing, MSAA)[1]是现代图形处理器和api事实上支持的方法。基于预过滤的方法[25,39,22,2,52,23]通过在渲染前预先计算内容的过滤版本,减轻了这一负担,因此,这种方法流更适合实时渲染。
- 在NeRF的背景下,超级采样可以通过每像素投射多个光线并聚合渲染结果来产生最终颜色来实现。这种简单的策略很有用,但代价很高,因为计算成本随着采样率的增加而显著增加。另一方面,最近的研究(MipNeRF/360, BACON)通过提出的集成位置编码或带限坐标网络将预滤波思想引入神经辐射场,以学习场景的预滤波表示,从而使其渲染在近距离视图中不模糊,在远距离视图中不混联。但是,它们的渲染和重建速度非常慢,例如MipNeRF[3]重建一个场景大约需要三天,渲染一帧需要几分钟,这阻碍了它们的适用性。相比之下,我们的Tri-MipRF可以在5分钟内重建,并在相同的硬件上实现实时渲染,同时我们的方法在近景和远景上都比MipNeRF具有更好的渲染质量。
Accelerating NeRF NeRF[35]隐式地表示MLP中的场景,这导致了非常紧凑的存储,但它的重建和渲染非常慢。一些研究致力于加速渲染,通过将场景分成许多单元[42,43]来降低推理复杂性,学习减少每条射线的样本[27,38],或缓存训练好的字段值[20,17,56,6]来减少渲染中的计算。另一项工作侧重于通过直接优化显式表示或利用混合表示,如低秩张量[9]和哈希表[37]来加快收敛速度,从而减少重构时间。特别是,哈希编码可以在5分钟左右的时间内实现即时重建和实时渲染。
- 但是,以上几种方法的渲染模型都存在将像素作为单个点进行采样而忽略对应区域的缺陷,这会导致近景渲染过于模糊,远景渲染过度混叠。上面提到的超级采样技术可以缓解这个问题,但需要每像素投射多次光线,这大大增加了重建和渲染成本。由于哈希冲突,将预过滤与哈希编码结合起来[37]是non-trivial的。我们的方法通过提出的Tri-Mip编码来解决这个问题,有效地对预过滤的3D特征空间进行建模,这与哈希编码一样有效,但能够产生抗混叠的高保真渲染。
Compact 2D representation for 3D content 直接在volumes中表示3D内容是内存和计算密集型的,而且由于3D内容总是稀疏的,因此是冗余的。Peng等[41]提出将点云的特征投影到多个平面进行三维几何重建。最近的研究[21,54,55]表明,3D内容可以在2D图像中紧凑地表示,并忠实地还原。在生成模型的背景下,EG3D[8]提出了一种三平面表示,将3D体积分解为三个二维平面进行3D内容生成,并在后续的许多生成方法中采用了这种表示[16,44,45,48,5,53,12]。此外,将这种表示进一步推广到四维空间中,以模拟动态场景[7,13]。我们的Tri-Mip编码就是受到这一行作品的启发,但是以上的表示都不能实现我们的目标,即对预滤波的3D特征空间进行建模,以实现有效的面积采样。
Method
Overview

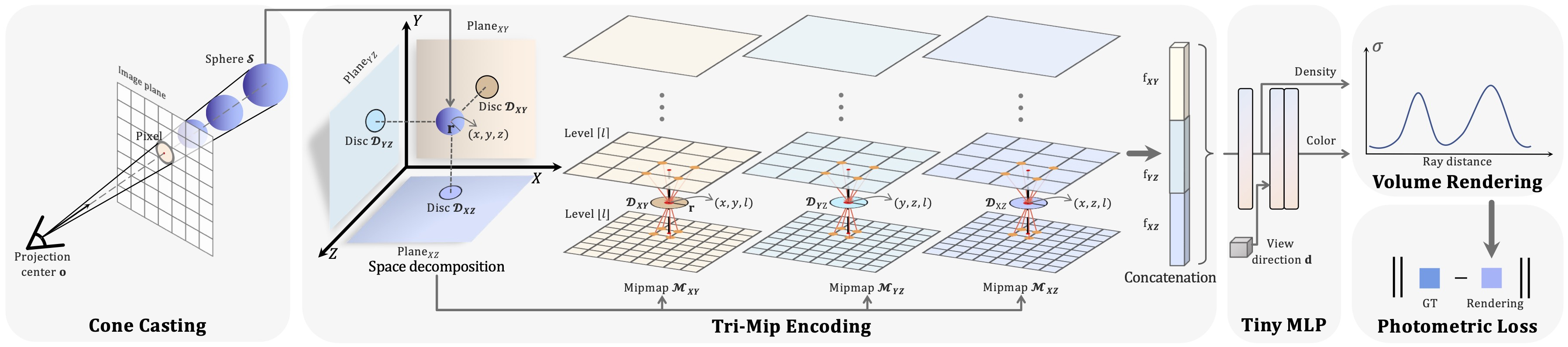
- 从相机原点出发,向成像平面上的像素圆盘发射一个圆锥C,并用一组与该圆锥内嵌的球体S对该圆锥进行采样
- 通过Tri-Mip Encoding(由三个minmaps M参数化)将球体S特征化为特征向量f,这是使我们的渲染图在近处视图中包含细粒度细节和在远处视图中没有混化的关键,因为Tri-Mip编码通过利用mipmap中的不同level有效地建模预过滤的3D特征空间。
- 然后,我们使用一个由权重Θ参数化的微小MLP将球体S的特征向量f和视图方向d非线性映射到球体的密度τ和颜色c :$[\tau,c]=\mathrm{MLP}(\mathbf{f},\mathbf{d};\Theta).$
- 最后,利用估算的圆锥体内球体的密度和颜色,通过[33]中的数值正交近似体绘制积分,绘制圆锥体对应像素的最终颜色:
$\begin{aligned}\mathbf{C}(\mathbf{t},\mathbf{d},\Theta,\mathcal{M})&=\sum_iT_i(1-\exp(-\tau_i(t_{i+1}-t_i)))c_i,\\\mathrm{with}\quad T_i&=\exp\left(-\sum_{k<i}\tau_k(t_{k+1}-t_k)\right)\end{aligned}$
- 通过计算loss,并反向传播优化MLP的权重参数$\Theta$和Tri-Mip编码中mipmaps的参数M
Cone Casting
PE/IPE: 位置编码,与显式或混合体积特征编码不兼容
HashGrid Encoding: 显式或混合体积特征编码
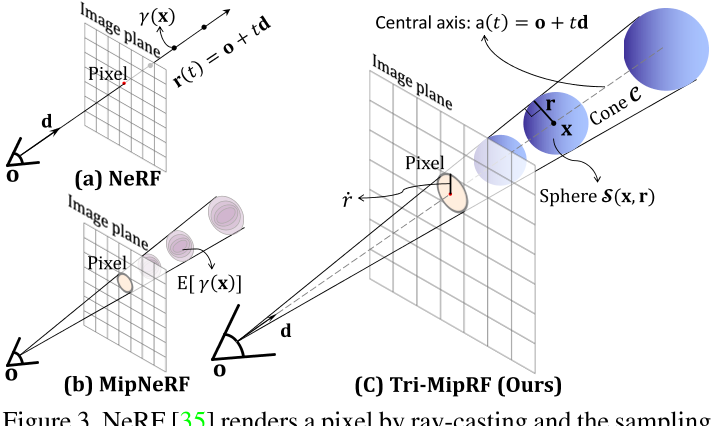
- NeRF:将像素看成一个点,从相机原点向像素点发出光线,沿着光线采样点的坐标,并利用位置频率编码$\gamma(\cdot)$对其进行特征化,得到点的特征向量
- 该公式将像素建模为单个点,而忽略像素的面积,这与现实世界的成像传感器有很大不同。大多数NeRF作品[47,56,14,9,10],包括instant-ngp[37],都遵循了这个公式。当捕获/渲染的视图处于大致恒定的距离时,它可以近似于现实世界的情况,但当在非常不同的距离上观看时,它会导致明显的伪影,例如,在特写视图中模糊,在远距离视图中混化,因为采样与距离无关。(近处的采样与远处的采样都是一个点)
- MipNeRF:为每个像素发出一个锥体,并对锥体进行多元高斯采样,再通过集成位置编码(IPE)对其进行特征化。IPE由E[γ(x)]对高斯范围内点的PE积分推导而来,如图3 (b)所示。
- 然而,该策略对于扩展到显式或混合表示以实现高效重建和渲染并非易事,例如,哈希编码[37],因为IPE是基于坐标的位置编码的积分,这与显式或混合体积特征编码不兼容。
- 相比之下,我们的高效锥形投射策略可以有效地与我们的Tri-Mip编码一起在体绘制期间进行区域采样。如图3 (c)所示,我们将像素表示为图像平面上的一个圆盘,而不是忽略像素面积的单个点。圆盘的半径可通过$\dot r = \sqrt{(∆x·∆y)/π}$计算,其中∆x和∆y为像素在世界坐标下的宽度和高度,可由标定后的相机参数导出。对于每个像素,我们从相机的投影中心沿方向$\mathbf{d} = \mathbf{p_{o}} - \mathbf{o}$发射一个圆锥C,其中$p_{o}$是像素的中心。圆锥体的顶点位于相机的光学中心,圆锥体与成像平面的交点是像素对应的圆盘。我们可以推导出圆锥的中轴线为$\mathbf{a(t)} = \mathbf{o} + t\mathbf{d}$。为了对锥体进行采样,我们不能遵循MipNeRF[3]使用多元高斯,因为多元高斯是各向异性的,而我们的Tri-Mip编码中的预滤波是各向同性的。
- 因此,我们用一组球体(x, r)对圆锥体进行采样,这些球体的圆心为x,半径为r。圆心x位于圆锥体的中心轴,半径为r,使球体与圆锥体相切,可以写成:
$\begin{aligned}\mathrm{x}&=\mathrm{o}+t\mathrm{d},\\\mathrm{r}&=\frac{|\mathrm{x}-\mathrm{o}|_2\cdot f\dot{r}}{|\mathrm{d}|_2\cdot\sqrt{\left(\sqrt{|\mathrm{d}|_2^2-f^2}-\dot{r}\right)^2+f^2},}\end{aligned}$
- 焦距f
- $\dot r = \sqrt{(∆x·∆y)/π}$
可得:采样球体S(x,r) 可以由$t_{i} \in t$确定
我们在摄像机预定义的近平面$t_{n}$和远平面$t_{f}$之间,或者在感兴趣的3D空间的圆锥体中心轴和轴向边界盒(AABB)之间的两个交点之间均匀地采样$t_{i} \in t$。为了进一步利用3D空间的稀疏性来加速cone casting,我们采用了一种二元占用网格,它粗略地标记了空与非空的空间,类似于(NGP or NerfAcc),这样我们可以便宜地跳过空区域的样本,并将样本集中在表面附近,以避免浪费计算。
Tri-Mip Encoding
为了实现我们的目标,即在近距离视图中呈现细粒度细节,在保持重建和渲染效率的同时避免在远距离视图中混叠,我们应该根据采样球体的占用面积对其S(x, r)进行constructively 特征化,这与计算机图形学中的区域采样(即预滤波)的动机相似。在instant-ngp中提出的哈希编码[37]可以通过查找哈希表和三线性插值来有效地表征采样点,然而,它不能轻易地扩展到表征球体S(x, r)。一个可行的解决方案是将超采样策略与哈希编码结合起来,以近似球体的特征。然而,超采样极大地增加了计算成本,出乎意料地牺牲了高效重构和渲染的能力。
为此,我们提出了一种新颖的Tri-Mip编码,由三个可训练的mipmap M参数化,以表征采样球体S(x, r):
$\begin{aligned}\mathbf{f}&=\text{Tri-Mip}(\mathbf{x},\mathbf{r};\mathcal{M}),\\\mathcal{M}&=\{\mathcal{M}_{XY},\mathcal{M}_{XZ},\mathcal{M}_{YZ}\}.\end{aligned}$
如图2所示,Tri-Mip编码使用正交投影将三维空间分解为三个平面(planeXY、planeXZ和planeYZ),然后用mipmap ($\mathcal{M}_{XY},\mathcal{M}_{XZ},\mathcal{M}_{YZ}$)表示每个平面,对预滤波的特征空间进行建模。对于每个mipmap,基层$M^{L_{0}}$是一个形状为H × W × C的特征图,其中H、W、C分别为通道的高度、宽度和数量。基层$M^{L_{0}}$随机初始化,可在重构过程中进行训练,其他层次$(M^{L_{i}}, i = 1,2,…, N)$是通过先前水平$M^{L_{i−1}}$沿高度和宽度降2倍而得到。该预滤波策略保持了mipmap各层之间的一致性,这是实现重建目标在不同距离上的相干性的关键。

为了查询球体S(x, r)对应的特征向量f,我们首先将S正交投影到三个平面上,得到三个discs圆盘$\mathcal{D} = \{\mathcal{D}_{XY}, \mathcal{D}_{XZ}, \mathcal{D}_{YZ}\}$,如图2所示。对于每个圆盘,我们从相应的mipmap中查询一个特征向量。
以磁盘$\mathcal{D}_{XY}$为例,我们从mipmap $\mathcal{M}_{XY}$中查询其特征$f_{XY}$。基于正交投影的性质,圆盘$\mathcal{D_{XY}}$与被采样球体具有相同的半径r,并且DXY的中心xDXY的二维坐标为被采样球体中心x(x, y, z)的偏坐标(x, y)。对于mipmap $\mathcal{M}_{XY}$的query level $l$,我们将其赋值为:
- $\ddot{r}$为基层$\mathcal{M}^{L_{0}}$特征元素的半径
- $\mathcal{B}_max$ 和$\mathcal{B}_{min}$分别是interested-3D space的AABB(Axis Aligned Bounding Box)最大和最小角
- 目的是将球体的半径r与mipmap $\mathcal{M}^{l}_{XY}$的某level 的特征元素的半径进行匹配。
在获得查询坐标(x, y, l)后,我们可以通过三线性插值从mipmap $\mathcal{M}_{XY}$得到特征向量$f_{XY}$。如图2所示,我们首先找到mipmap的两个最近的层$\mathcal{M}_{XY}^{\lfloor l\rfloor}$和$\mathcal{M}_{XY}^{\lceil l\rceil}$然后我们将圆盘$\mathcal{D}_{XY}$的中心坐标(x, y)投影到mipmap的两层(以红点表示);接下来,我们分别找到它们的四个邻居(用橙色点表示);最后,我们根据八个相邻点到光盘$\mathcal{D}_{XY}$中心的距离进行插值,得到特征向量$f_{XY}$。三线性插值不仅提高了层次和空间分辨率的有效精度,而且产生了连续的编码空间,有利于提高训练效率。同样,我们可以分别得到圆盘$\mathcal{D}_{XZ}$和$\mathcal{D}_{YZ}$的特征向量$f_{XZ}$和$f_{YZ}$。采样球体S的最终查询特征向量f是三个圆盘特征向量$\{f_{XY}, f_{XZ}, f_{YZ}\}$的连接。
我们的 Tri-Mip 编码以预过滤的方式有效地对 3D 空间进行特征化,以便我们可以对体积渲染执行区域采样以产生没有混叠的高质量渲染。特征查询过程也很有效,即在现代 GPU 中查询 mipmap是已经高度优化的,这促进了快速重建。
此外,我们的 Tri-Mip 编码的存储是三个 2D 特征图,即三个 mipmap $M^{l_{0}}$ 的基本级别,因为其他级别由基础级别通过downscaling导出,这使得我们的模型足够紧凑以便于分布。请注意,Tri-Mip 编码还促进了训练的收敛速度比隐式表示 MLP 中的场景更快,例如,我们的方法只需要 25K 次迭代收敛,而 MipNeRF [3] 需要 1M 次迭代,因为 mipmap M 中的特征可以直接优化,而不是通过 MLP 的可优化权重从 IPE 映射。
Hybrid Volume-Surface Rendering
虽然我们的方法可以有效地重建辐射场,但直接在消费级gpu上进行渲染,例如。Nvidia RTX 3060显卡只能达到30 FPS左右。这是因为体积渲染固有地为每个像素在锥体内采样多个球体,尽管我们可以通过二进制占用网格跳过一些采样。
观察到多边形网格的高效栅格化对实时表面渲染的好处,我们开发了一种混合体面渲染策略来进一步提高渲染速度除了重建的辐射场外,我们的混合体面渲染策略还需要一个代理网格来有效地确定从相机光学中心到物体的粗略距离。幸运的是,我们可以通过在重建的密度场上marching cubes[PDF] Marching cubes: A high resolution 3D surface construction algorithm-论文阅读讨论-ReadPaper,然后mesh decimation网格抽取来获得代理网格。我们的Tri-MipRF生成的代理网格即使在复杂的结构细节中也具有高保真的质量,如图4 (a)的左侧所示,而Instant-ngp[37]和neus[49]生成的结果作为参考显示在右侧。
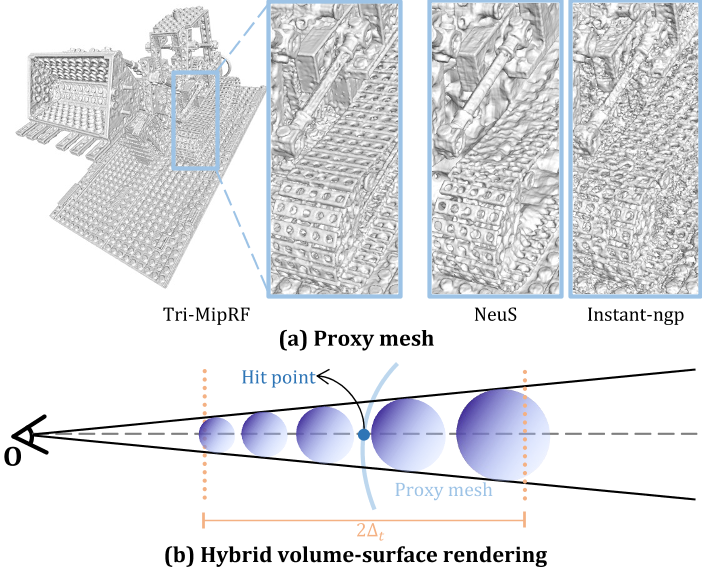
一旦代理网格可用,我们首先对其进行有效栅格化,以获得圆锥体中轴线表面上的命中点(如图4 (b)所示),然后我们在距圆锥体中轴线命中点∆t距离内均匀采样球体,这产生2∆t采样间隔。这种混合体面渲染策略显著减少了样本数量,从而在消费者级gpu上实现实时渲染(>60 FPS)。请参阅补充材料中的视频,以获得实时交互式渲染演示
Experimental Evaluation
Implementation
- 我们将每个像素的损失按其在图像平面上的足迹面积进行缩放,称为“面积损失”:$\mathcal{L}_{area}$
- 使用tiny-cuda-nn扩展来实现
- 使用nvdiffrast库实现Tri-Mip编码[PDF] Modular Primitives for High-Performance Differentiable Rendering-论文阅读讨论-ReadPaper (zhihu.com)
- mipmap基层形状$M^{L_{0}}$被经验地设置为H = 512, W = 512, C = 16
- MLP:
- 使用AdamW优化器:25K iteration
- weight decay set to $1 × 10^{−5}$
- learning ratelearning :$2 × 10^{-3}$
- MultiStepLR scheduled
- 使用AdamW优化器:25K iteration
- Encoding:
- lr : $2 × 10^{-2}$
Evaluation on the Multi-scale Blender Dataset
比较指标: