Zip-NeRF

Title	Zip-NeRF: Anti-Aliased Grid-Based Neural Radiance Fields
Author	Jonathan T. BarronBen MildenhallDor VerbinPratul P. SrinivasanPeter Hedman
Conf/Jour	ICCV
Year	2023
Project	Zip-NeRF (jonbarron.info)
Paper	Zip-NeRF: Anti-Aliased Grid-Based Neural Radiance Fields (readpaper.com)

Zip-NeRF在抗混叠(包括NeRF从空间坐标到颜色和密度的学习映射的空间混叠，以及沿每条射线在线蒸馏过程中使用的损失函数的z-混叠)方面都取得了很好的效果，并且速度相比前作Mip-NeRF 360 提高了24X

mipNeRF 360+基于网格的模型(如Instant NGP)的技术

• 错误率下降8~77%，并且比Mip-NeRF360提速了24X
• 主要贡献：
  • 多采样
  • 预滤波

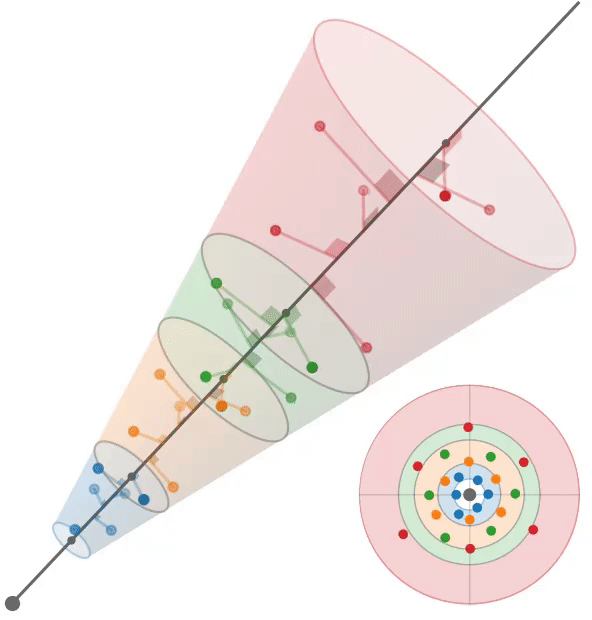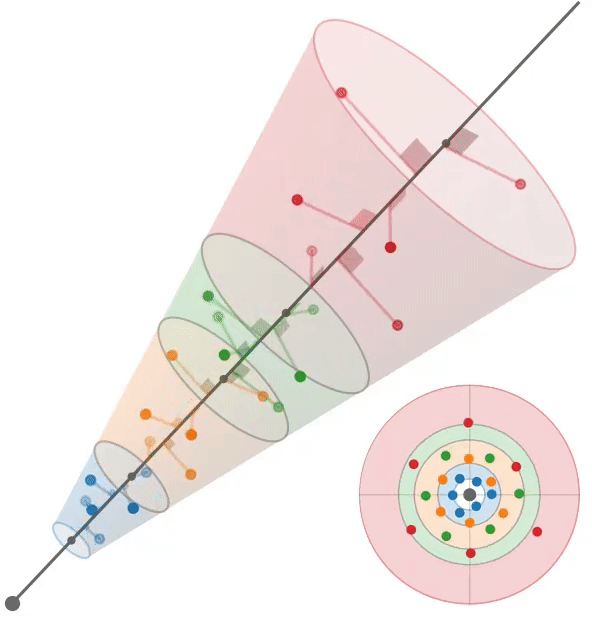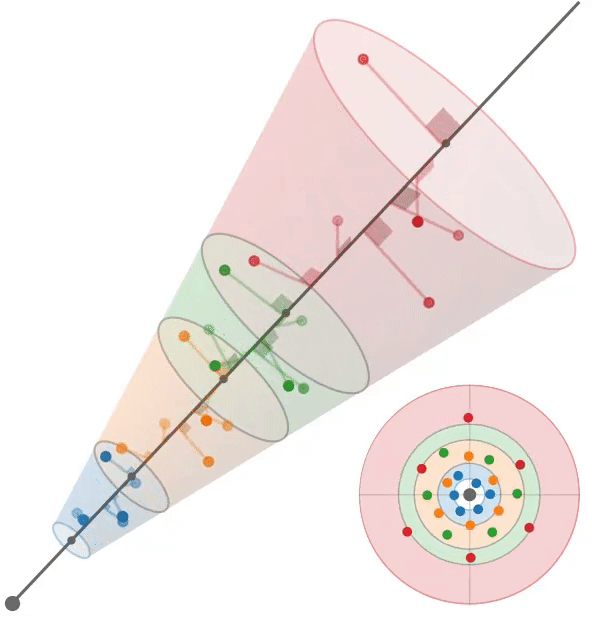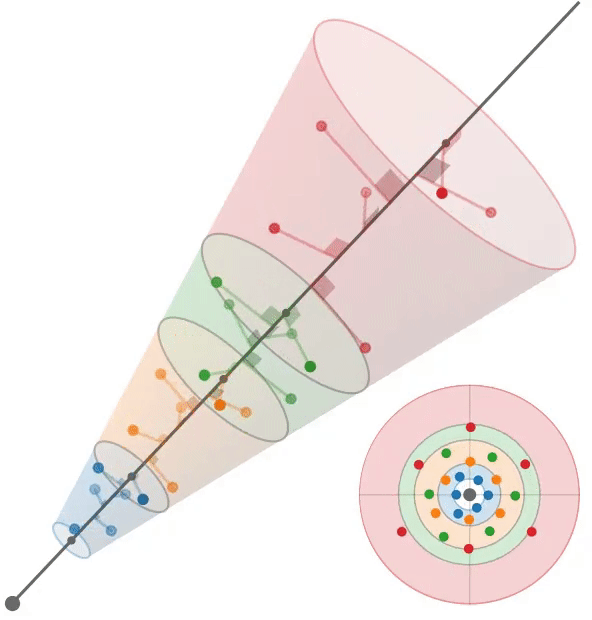
多采样：train左，test右

Conclusion

We have presented Zip-NeRF, a model that integrates the progress made in the formerly divergent areas of scaleaware anti-aliased NeRFs and fast grid-based NeRF training.

By leveraging ideas about multisampling and prefiltering, our model is able to achieve error rates that are 8% – 77% lower than prior techniques, while also training 24×faster than mip-NeRF 360 (the previous state-of-the-art on our benchmarks).

We hope that the tools and analysis presented here concerning aliasing (both the spatial aliasing of NeRF’s learned mapping from spatial coordinate to color and density, and z-aliasing of the loss function used during online distillation along each ray) enable further progress towards improving the quality, speed, and sample-efficiency of NeRF-like inverse rendering techniques.

Abstract

神经辐射场训练可以通过在NeRF的学习映射中使用基于网格的表示来加速，从空间坐标到颜色和体积密度。然而，这些基于网格的方法缺乏对尺度的明确理解，因此经常引入混叠，通常以锯齿或缺失场景内容的形式出现。
mip-NeRF 360之前已经解决了抗锯齿问题，它可以沿锥体而不是沿射线的点来计算子体积，但这种方法与当前基于网格的技术不兼容。

我们展示了如何使用渲染和信号处理的想法来构建一种结合mipNeRF 360和基于网格的模型(如Instant NGP)的技术，其错误率比之前的技术低8% - 77%，并且训练速度比mip-NeRF 360快24倍。

Introduction

• NeRF：原始的NeRF模型使用多层感知器(MLP)来参数化从空间坐标到颜色和密度的映射。尽管mlp结构紧凑且富有表现力，但训练速度较慢。
• 最近的研究已经通过用类似体格voxel-grid-like的数据结构替换或增强mlp来加速训练[7,15,27,35]。一个例子是Instant-NGP (iNGP)，它使用粗网格和细网格的pyramid(其中最细的网格使用hash map存储)来构建由微小MLP处理的学习特征，从而大大加速了训练[21]。
• 除了速度慢之外，最初的NeRF模型也被混淆了: NeRF对光线中的单个点进行推理，这会导致渲染图像中的“锯齿”，并限制NeRF对比例的推理能力。
• Mip-NeRF[2]通过投射锥体而不是射线解决了这个问题，并将整个体积置于锥形锥内，用作MLP的输入。Mip-NeRF及其后续产品mipNeRF 360[3]表明，这种方法可以在具有挑战性的现实场景中实现高精度渲染
• 令人遗憾的是，在快速训练和抗混叠这两个问题上取得的进展，乍一看是互不相容的。这是因为mip-NeRF的抗锯齿策略主要依赖于使用位置编码[28,30]将锥形锥台特征化为离散特征向量，但当前基于网格的方法不使用位置编码，而是使用通过插值到单个3D坐标的网格层次中获得的学习特征。尽管在渲染中抗锯齿是一个研究得很好的问题[8,9,26,31]，但大多数方法并不能自然地推广到像iNGP这样基于网格的NeRF模型中的反渲染。
• 在这项工作中，我们利用多采样、统计和信号处理的想法，将iNGP的网格pyramid集成到mip-NeRF 360的框架中。我们称我们的模型为“Zip-NeRF”，因为它的速度，它与mipNeRF的相似性，以及它修复类似拉链的混叠工件的能力。在mip-NeRF 360基准测试[3]上，Zip-NeRF将错误率降低了19%，训练速度比以前的最先进技术快24倍。在该基准的多尺度变体中，Zip-NeRF更彻底地测量了混联和尺度，错误率降低了77%。

Preliminaries

Mip-NeRF 360和Instant NGP (iNGP)都是类似nerf的:通过投射3D光线和沿着光线距离t的特征位置来渲染像素，并将这些特征馈送到神经网络，神经网络的输出是$\alpha-composited$合成来渲染颜色。训练包括重复投射与训练图像中像素对应的光线，并最小化(通过梯度下降)每个像素的渲染和观察到的颜色之间的差异。
Mip-NeRF 360和iNGP在如何参数化射线坐标方面有很大的不同。在mip-NeRF 360中，射线被细分为一组区间$[t_i, t_{i+1})$，每个区间代表一个圆锥形截锥体，其形状由多元高斯近似表示，与该高斯相关的期望位置编码被用作大型MLP的输入[2]。相比之下，iNGP三线性插值到不同大小的3D网格层次中，为小型MLP生成特征向量[21]。我们的模型结合了mip-NeRF 360的整体框架和iNGP的特征化方法，但将这两种方法天真地结合起来会引入两种形式的混联:

• InstantNGP的特征网格方法与mip- nerf360的感知尺度的集成位置编码技术不兼容，因此iNGP生成的特征相对于空间坐标是混叠aliased的，从而产生aliased的渲染图。在第2节中，我们通过引入一种用于计算预滤波的iNGP特征的类似多采样的解决方案来解决这个问题
• 使用iNGP极大地加速了训练，但这揭示了mip-NeRF 360的在线蒸馏方法的问题，导致高度可见的“z-混叠”(沿着光线混叠)，其中场景内容随着相机移动而不规律地消失。在第3节中，我们用一个新的损失函数来解决这个问题，该损失函数在计算用于监督在线蒸馏的损失函数时沿每条射线进行预过滤。

Spatial Anti-Aliasing

Mip-NeRF使用的特征近似于子体中坐标位置编码的积分，这是一个锥形截锥体。这导致当特征正弦波的周期大于高斯的标准差时，其傅立叶特征振幅较小-这些特征仅在大于子体尺寸的波长处表示子体的空间位置。由于该特征对位置和比例进行编码，因此使用它的MLP能够学习呈现抗混叠图像的3D场景的多尺度表示。像iNGP这样基于网格的表示本身不允许查询sub-volumes，而是在单点使用三线性插值来构建用于MLP的特征，这导致学习模型无法对规模或混叠进行推理。
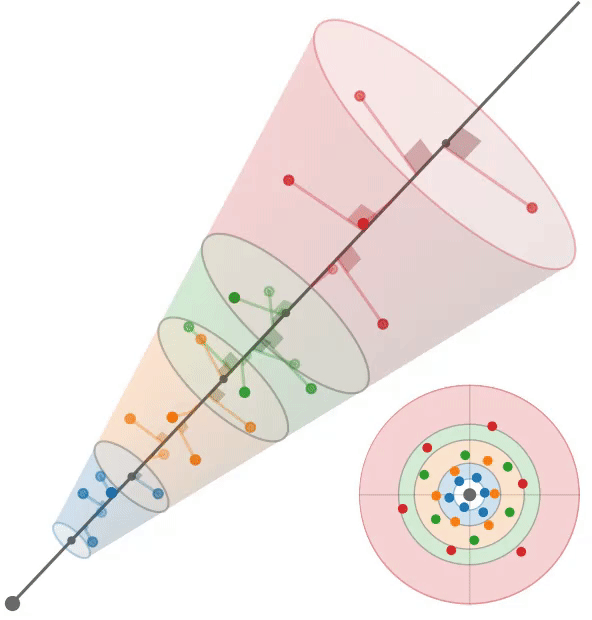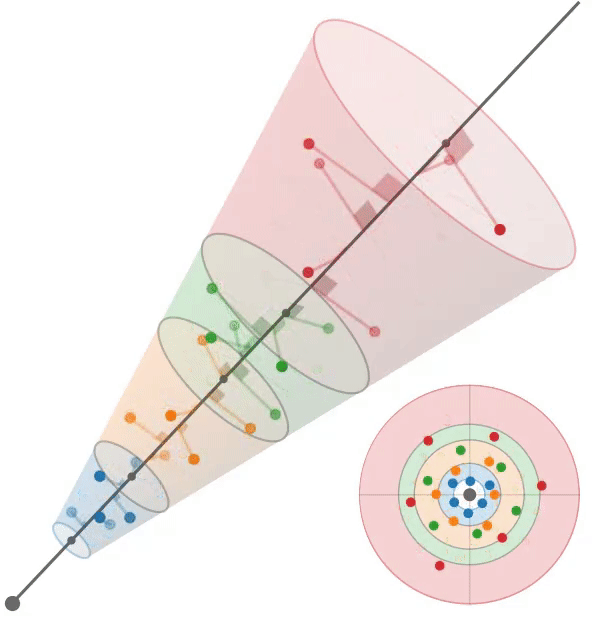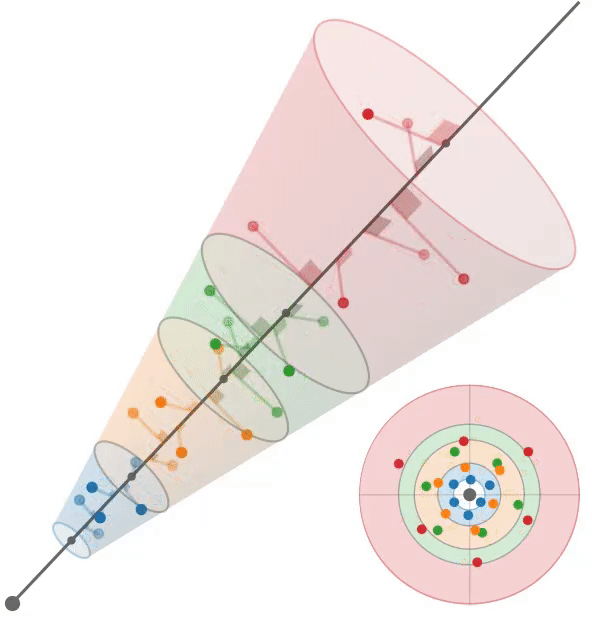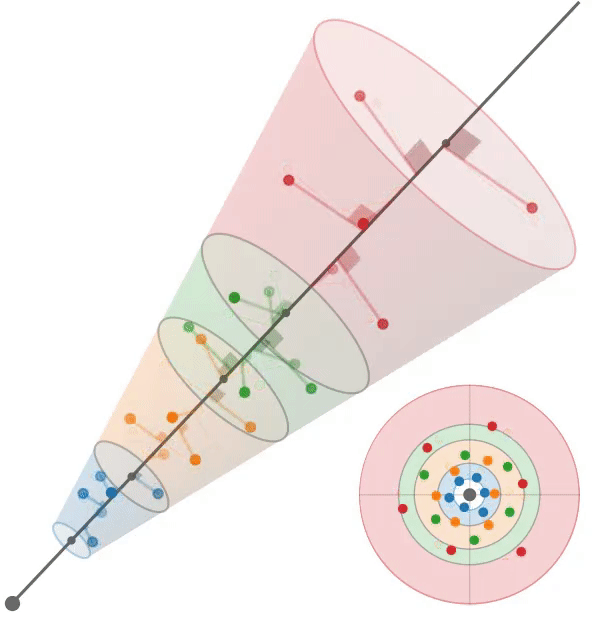
我们通过将每个锥形截锥体转换为一组各向同性高斯体来解决这个问题，使用多重采样和特征降权的组合: 各向异性子体首先转换为一组近似其形状的点，然后假设每个点是具有一定尺度的各向同性高斯体。这种各向同性假设使我们能够利用网格中的值为零均值的事实来近似特征网格在子体积上的真实积分。通过平均这些降权特征，我们从iNGP网格中获得了尺度感知的预滤波特征。如图2所示。

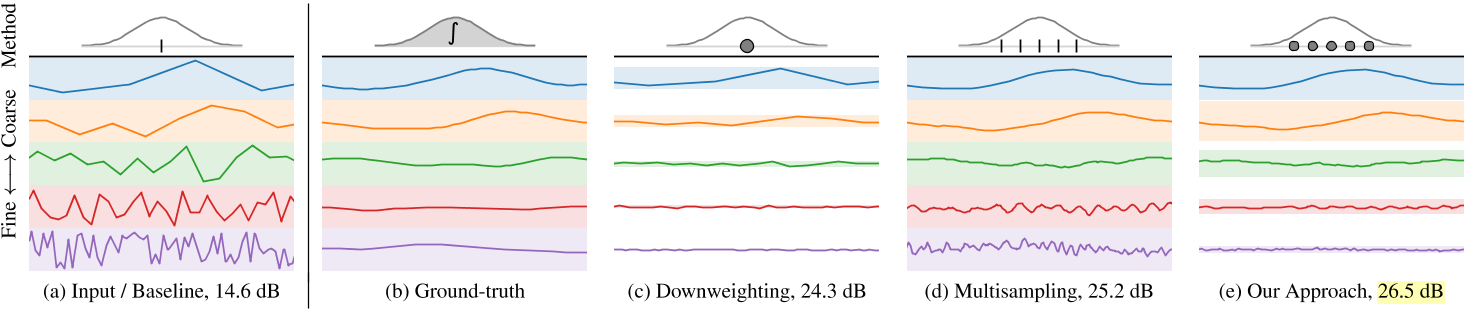
这里我们展示了一个toy的一维iNGP[21]，每个尺度有一个特征。每个子图表示沿x轴在所有坐标上查询iNGP的不同策略——想象一个从左向右移动的高斯函数，其中每条线是每个坐标的iNGP特征，其中每种颜色是iNGP中的不同比例。(a)查询高斯均值的朴素解决方案导致具有分段线性扭曲的特征，其中超过高斯带宽的高频很大且不准确。(b)通过将iNGP特征与高斯函数卷积得到的真实解——在实践中是一个棘手的解——得到光滑但信息丰富的粗糙特征和接近0的精细特征。(c)我们可以通过基于高斯尺度的降权来抑制不可靠的高频(每个特征后面的颜色带表示降权)，但这会导致粗糙特征中不自然的尖锐不连续。(d)或者，超采样产生合理的粗尺度特征，但产生不稳定的细尺度特征。(e)因此，我们多样本各向同性亚高斯分布(如图5所示)，并使用每个亚高斯分布的尺度来降低频率的权重。

抗锯齿在图形学文献中得到了很好的探讨。Mip mapping(Mip - nerf的同名)预先计算了一种能够快速抗锯齿的数据结构，但目前尚不清楚这种方法如何应用于iNGP的基于哈希的数据结构。超采样技术[8]采用蛮力方法抗混叠，使用大量样本;我们将证明，这种方法比我们的方法效率更低，成本更高。多采样技术[11]构建一个小样本集，然后将这些多样本中的信息汇集到一个聚合表示中，并提供给一个昂贵的渲染过程——这是一种类似于我们的方法的策略。

Multisampling

根据mip-NeRF[2]，我们假设每个像素对应一个半径为$\dot r t$的锥，其中沿射线的距离为t。给定沿射线$[t_0, t_1]$的一个区间，我们想要构造一组近似于该锥形截锥体形状的多样本。我们使用一个六点六边形图案，其角$θ_j$为:$\theta=\left[\begin{matrix}0,2\pi/3,4\pi/3,3\pi/3,5\pi/3,\pi/3\end{matrix}\right],$
它们是线性间隔的角，围绕一个圆旋转一次，排列成一对位移60度的三角形。沿着射线$t_{j}$的距离是:

$$\begin{aligned}t_{j}&=t_{0}+\frac{t_{\delta}\left(t_{1}^{2}+2t_{\mu}^{2}+\frac{3}{\sqrt{7}}\left(\frac{2j}{5}-1\right)\sqrt{\left(t_{\delta}^{2}-t_{\mu}^{2}\right)^{2}+4t_{\mu}^{4}}\right)}{t_{\delta}^{2}+3t_{\mu}^{2}}\\\mathrm{where~}t_{\mu}&=(t_{0}+t_{1})/2,t_{\delta}=(t_{1}-t_{0})/2\end{aligned}$$

它们是$[t_0, t_1)$中的线性间隔值，经过位移和缩放以将质量集中在离截体远端的附近。我们的多样本坐标相对于射线是:

$$\left\{\begin{bmatrix}\dot{r}t_j\cos(\theta_j)/\sqrt{2}\\\dot{r}t_j\sin(\theta_j)/\sqrt{2}\\t_j\end{bmatrix}\Bigg|j=0,1,\ldots,5\right\}.$$

通过将这些3D坐标乘以一个标准正交基，将它们旋转成世界坐标，该标准正交基的第三个向量是射线方向(其前两个向量是垂直于射线的任意帧)，然后由射线原点移动。通过构造，这些多样本的样本均值和方差(沿射线方向和垂直于射线方向)与锥形截锥体的均值和方差完全匹配，类似于mip-NeRF高斯分布。在训练期间，我们随机旋转和翻转每个图案，在渲染期间，我们确定地翻转和旋转每个其他图案30度。图3显示了这两种策略的可视化。

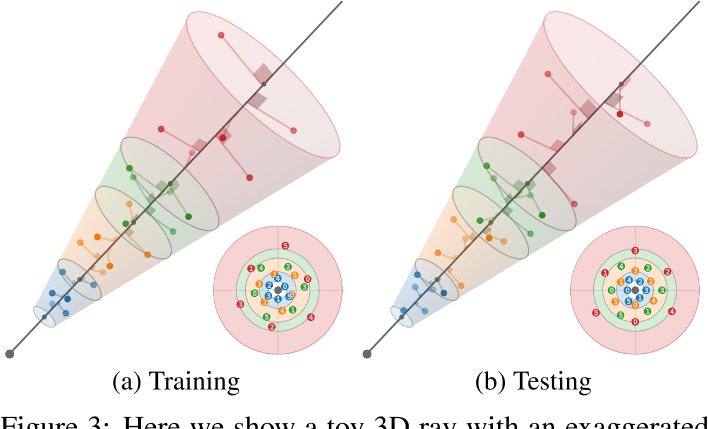
我们使用这6个多样本$\{x_{j}\}$作为各向同性高斯函数的平均值，每个高斯函数的标准差为$σ_j$。我们设置$σ_{j} = (\dot r t_{j} /√2)$，用一个超参数进行缩放，在所有实验中都是0.5。由于iNGP网格要求输入坐标位于有界域中，因此我们应用了mip-NeRF 360[3]中的收缩函数。由于这些高斯函数是各向同性的，我们可以使用mip-NeRF 360使用的卡尔曼滤波方法的有效替代方法来计算由这种收缩引起的比例因子;详见附录。

Downweighting

虽然多采样是减少混叠的有效工具，但对每个多采样使用朴素三线性插值仍然会导致高频混叠，如图2(d)所示。对于每个单独的多样本的抗混叠插值，我们以一种与每个多样本的各向同性高斯在每个网格单元中的拟合程度成反比的方式重新加权每个尺度的特征: 如果高斯比被插值到的单元大得多，则插值的特征可能不可靠，应该降低权重。Mip-NeRF的IPE特征也有类似的解释。

在iNGP中，对坐标x的每个$\{V_{\ell}\}$的插值是通过将x按网格的线性大小$n_{\ell}$缩放，并对$V_{\ell}$执行三线性插值以获得$c_{\ell}$长度的向量来完成的。我们用均值${x_j}$和标准差${σ_j}$插值一组多采样各向同性高斯函数。通过对高斯CDFs的推理，我们可以计算出在$V_{\ell}$中的$[−1/2n, 1/2n]^3$立方内的每个高斯PDF的分数，并将其插值为与比例相关的降权因子$ω_{j,\ell} = erf(1/\sqrt{8σ^{2}_{j} n^{2}_{\ell}})$，其中$ω_{j,\ell}∈[0,1]$。如第4节所述，我们对$\{V_{\ell}\}$施加权衰减，这促使$V_{\ell}$中的值呈正态分布且为零均值。这个零均值假设让我们将期望的网格特征相对于每个多样本的高斯近似为$\omega_{j}\cdot\mathbf{f}_{j,\ell}+(1-\omega_{j})\cdot\mathbf{0}=\omega_{j}\cdot\mathbf{f}_{j,\ell}.$。这样，我们就可以通过对每个多样本的插值特征进行加权平均，近似得到所要表征的圆锥截锥体所对应的期望特征:$\mathbf{f}_{\ell}=\max_{j}(\omega_{j,\ell}\cdot\mathrm{trilerp}(n_{\ell}\cdot\mathbf{x}_{j};V_{\ell})).$
这组特性$\{\mathbf{f}_{\ell}\}$被连接起来并作为输入提供给MLP，就像在iNGP中一样。我们还连接了$\{ω_{j,\ell}\}$的特征版本，详细信息请参见附录。

Z-Aliasing and Proposal Supervision

虽然前面详细介绍的多采样和降权方法是减少空间混叠的有效方法，但是我们必须考虑沿着射线的另一个混叠源，我们将其称为z-aliasing。这种z-aliasing是由于mip-NeRF 360使用了一个学习产生场景几何上界的提议MLP: 在训练和渲染期间，沿着射线的间隔被这个提议MLP反复评估，以生成直方图，由下一轮采样重新采样，只有最后一组样本由NeRF MLP渲染。Mip-NeRF 360表明，与之前使用图像重建来监督学习一个[2]或多个[19]nerf的策略相比，这种方法显著提高了速度和渲染质量。我们观察到mip-NeRF 360中的MLP倾向于学习从输入坐标到输出体积密度的非光滑映射。这导致了射线“跳过”场景内容的伪影，如图4所示。虽然这个工件在mip-NeRF 360中是微妙的，但如果我们为我们的提议网络使用iNGP后端而不是MLP(从而增加我们模型快速优化的能力)，它就会变得普遍和视觉上显著，特别是当相机沿着其z轴平移时。

mip-NeRF 360中z-混叠的根本原因是用于监督提案网络的“层间损失”，它将等效的损失分配给NeRF和提案直方图bins，无论它们的重叠是部分的还是完全的-提案直方图箱只有在它们完全没有重叠时才会受到惩罚。为了解决这个问题，我们提出了一种替代损耗，与mip-NeRF 360的层间损耗不同，它是沿射线距离连续且平滑的。图6是两种损失函数的比较。

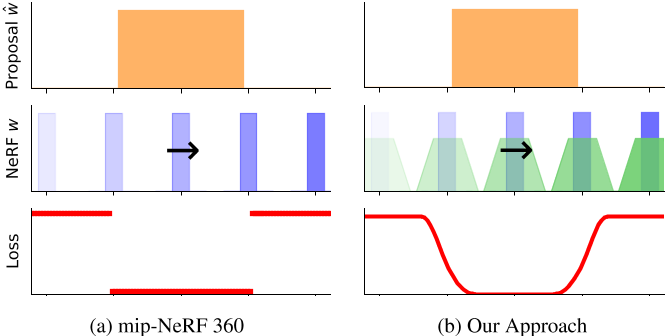
在这里，我们可视化了一个toy设置的提案监督，其中窄NeRF直方图(蓝色)沿着相对于粗提案直方图(橙色)的射线转换。(a) mip-NeRF 360使用的损失是分段常数，但(b)我们的损失是平滑的，因为我们将NeRF直方图模糊成分段线性样条(绿色)。我们的预过滤损失让我们学习反混叠提案分布。

Blurring a Step Function:
为了设计一个对沿射线的距离光滑的损失函数，我们必须首先构造一种将分段常数阶跃函数转化为连续分段线性函数的技术。平滑离散1D信号是微不足道的，只需要用盒滤波器(或高斯滤波器等)进行离散卷积。但是当处理端点连续的分段常数函数时，这个问题就变得困难了，因为阶跃函数中每个区间的端点可能在任意位置。栅格化阶跃函数并执行卷积并不是一个可行的解决方案，因为这在非常窄的直方图箱的常见情况下是失败的。

因此需要一种新的算法。考虑一个阶跃函数(x, y)，其中$(x_i, x_{i+1})$是区间i的端点，$y_i$是区间i内阶跃函数的值。我们想要将这个阶跃函数与半径为r的矩形脉冲进行卷积，该脉冲积分为1$:[|x| < r]/(2r)$，其中[]是艾弗森括号。观察到阶跃函数的单个区间i与该矩形脉冲的卷积是一个分段线性梯形，其结点为$(x_i−r, 0)， (x_i+ r, yi)， (x_i+1−r, y_i)， (x_i+1 + r, 0)$，而分段线性样条是位于每个样条结处的缩放三角函数的二重积分[12]。,和这一事实总和通勤与整合,我们可以有效地缠绕一个矩形脉冲的阶跃函数如下:我们把每个端点$x_i$的阶跃函数分成两个signed delta functions位于$x_i−r$和$x_i+r$值正比于相邻的y值之间的变化,我们交错(通过排序)δ函数,然后我们把这些排序δ函数两次(参见算法1补充的伪代码)。有了这个，我们可以构造我们的抗混叠损失函数。

Anti-Aliased Interlevel Loss:
我们继承的mip-NeRF 360中的提议监督方法需要一个损失函数，该损失函数以NeRF (s, w)产生的阶跃函数和提议模型$(\hat s, \hat w)$产生的类似阶跃函数作为输入。这两个阶跃函数都是直方图，其中s和$\hat s$是端点位置的向量，w和$\hat w$是权值之和≤1的向量，其中$w_i$表示场景内容在阶跃函数区间的可见程度。每个$s_i$是真度量距离$t_i$的某个归一化函数，根据某个归一化函数g(·)，我们将在后面讨论。请注意，s和$\hat s$是不相同的-每个直方图的端点是不同的。
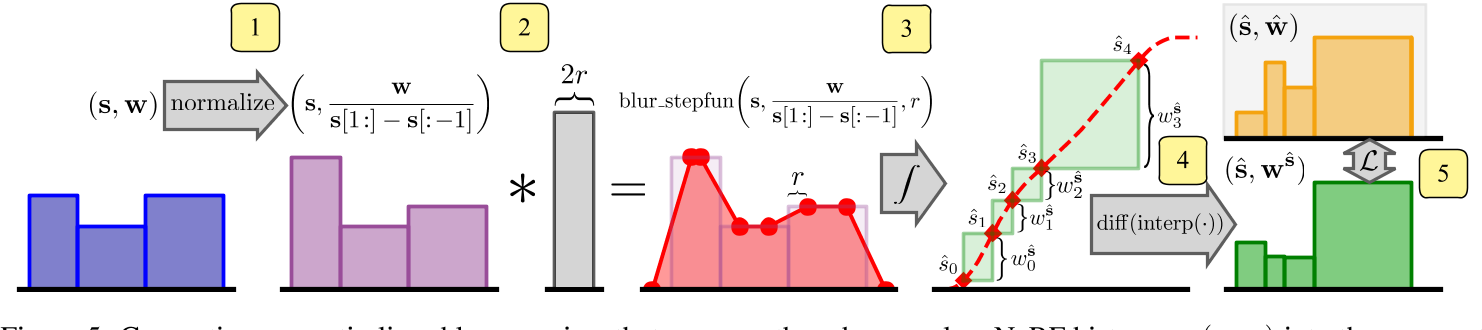
为了训练一个提议网络，在不引入混联的情况下约束NeRF预测的场景几何，我们需要一个损失函数，可以测量(s, w)和$(\hat s, \hat w)$之间的距离，该距离相对于沿着光线的平移是平滑的，尽管这两个阶跃函数的端点是不同的。为此，我们将使用我们之前构建的算法模糊NeRF直方图(s, w)，然后将模糊的分布重新采样到提议直方图的区间集中，以产生一组新的直方图权重$w^{\hat s}$。图5描述了这个过程。在将模糊的NeRF权重重新采样到提案直方图的空间后，我们的损失函数是$w^{\hat s}$和$\hat w$的元素函数:$\mathcal{L}_{\mathrm{prop}}(\mathbf{s},\mathbf{w},\hat{\mathbf{s}},\hat{\mathbf{w}})=\sum_{i}\frac{1}{\hat{w}_{i}}\max(0,\not\nabla(w_{i}^{\hat{\mathbf{s}}})-\hat{w}_{i})^{2}.$
虽然这种损失类似于mip-NeRF 360的损失(带有停止梯度的半二次卡方损失)，但用于生成$w^{\hat s}$的模糊和重采样可以防止混叠

计算我们的抗锯齿损失需要我们平滑和重新采样NeRF直方图(s, w)到与提议直方图$(\hat s, \hat w)$相同的端点集，我们在这里概述。(1)我们用w除以s内每个区间的大小，得到积分≤1的分段常数PDF。(2)我们将该PDF与矩形脉冲进行卷积，以获得分段线性PDF。(3)集成此PDF以生成分段二次CDF，该CDF通过分段二次插值在三元关系式的每个位置$\hat s$进行查询。(4)通过取相邻插值值之间的差值，我们得到$w^{\hat s}$，这是重新采样到提议直方图$\hat s$端点的NeRF直方图权值w。(5)重新采样后，我们将loss $\mathcal{L}_{prop}$评估为$w^{\hat s}$和$\hat w$的元素函数，因为它们共享一个公共的坐标空间。

Normalizing Metric Distance:
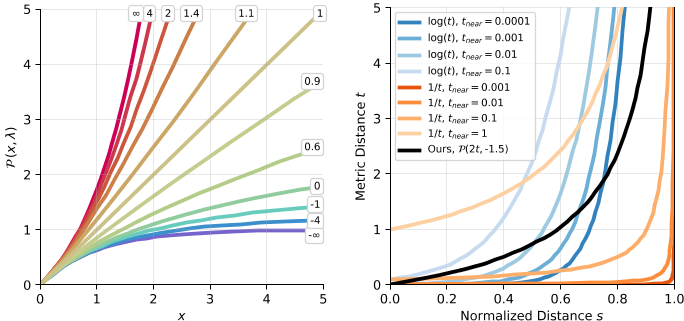
在mip-NeRF 360中，我们用归一化距离$s∈[0,1]$来参数化沿着射线$t∈[t_{near}, t_{far}]$的度量距离(其中tnear和tfar是手动定义的近和远平面距离)。渲染使用度量距离t，但重新采样和提案监督使用归一化距离s，其中一些函数g(·)定义了两者之间的双射。mip-NeRF 360中使用的层间损耗对距离的单调变换是不变的，因此它不受g(·)的选择的影响。然而，我们的抗混叠损失预滤波消除了这种不变性，并且在我们的模型中使用mip-NeRF 360’s g(·)会导致灾难性的失败，因此我们必须构建一个新的归一化。为此，我们构建了一个新的power转换:$\mathcal{P}(x,\lambda)=\frac{|\lambda-1|}{\lambda}\left(\left(\frac{x}{|\lambda-1|}+1\right)^{\lambda}-1\right).$
该函数在原点处的斜率为1，因此射线原点附近的归一化距离与度量距离成正比(无需调整非零的近平面距离曲线)，但远离原点的度量距离变得弯曲，类似于对数距离(λ = 0)或逆距离(λ = - 1)。这让我们可以在不同的归一化之间平滑地插值，而不是在不同的离散函数中交换。如图7所示为P(x， λ)的可视化，以及与我们的归一化方法的比较，即$g(x) = \mathcal{P}(2x， - 1.5)$ , 当$s∈[0,1 /2]$时，该曲线大致为线性，但当$s∈[1/2,1]$时，该曲线介于逆和反平方之间

Results

我们的模型是在JAX[6]中实现的，基于mip-NeRF 360代码库[20]，重新实现了iNGP的体素网格金字塔和哈希值，取代了mip-NeRF 360使用的大型MLP。我们的整体模型架构与mip-NeRF 360相同，除了第2节和第3节中引入的抗锯齿调整，以及我们在这里描述的一些额外修改。

像mip-NeRF 360一样，我们使用两轮提议采样，每次64个样本，然后在最后的NeRF采样轮中使用32个样本。我们的抗混叠级间损失被施加在两轮提议采样上，第一轮的矩形脉冲宽度为r = 0.03，第二轮为r = 0.003，损耗乘数为0.01。我们对每一轮提议采样使用单独的提议iNGP和MLP，并且我们的NeRF MLP使用比iNGP使用的更大的依赖于视图的分支。详见附录。

我们对iNGP做的一个小而重要的修改是对存储在其网格和哈希金字塔中的特征代码施加标准化的权重衰减:$\sum_\ell\operatorname{mean}(V_\ell^2).$。通过惩罚每个金字塔级别$V_{\ell}$的方格网格/哈希值的平均值的和，我们诱导出与惩罚所有值的和的naive解决方案截然不同的行为，因为粗尺度比细尺度受到的惩罚要多几个数量级。这个简单的技巧非常有效——与没有权重衰减相比，它大大提高了性能，并且显著优于朴素权重衰减。在所有实验中，我们对这个归一化权重衰减使用0.1的损失乘数。

• 360 Dataset
• Multiscale 360 Dataset

实验

非论文code

SuLvXiangXin/zipnerf-pytorch: Unofficial implementation of ZipNeRF (github.com)

环境配置

# Clone the repo.
git clone https://github.com/SuLvXiangXin/zipnerf-pytorch.git
cd zipnerf-pytorch

# Make a conda environment.
conda create --name zipnerf python=3.9
conda activate zipnerf

# Install requirements.
pip install -r requirements.txt

# Install other extensions
pip install ./gridencoder

# Install nvdiffrast (optional, for textured mesh)
git clone https://github.com/NVlabs/nvdiffrast
pip install ./nvdiffrast

# Install a specific cuda version of torch_scatter 
# see more detail at https://github.com/rusty1s/pytorch_scatter
CUDA=cu117
pip install torch-scatter -f https://data.pyg.org/whl/torch-2.0.0+${CUDA}.html

Train

• Dataset

mkdir data
cd data

# e.g. mipnerf360 data
wget http://storage.googleapis.com/gresearch/refraw360/360_v2.zip
unzip 360_v2.zip

• Train

# Configure your training (DDP? fp16? ...)
# see https://huggingface.co/docs/accelerate/index for details
accelerate config

# Where your data is 
DATA_DIR=data/360_v2/bicycle
EXP_NAME=360_v2/bicycle

# Experiment will be conducted under "exp/${EXP_NAME}" folder
# "--gin_configs=configs/360.gin" can be seen as a default config 
# and you can add specific config useing --gin_bindings="..." 
accelerate launch train.py \
    --gin_configs=configs/360.gin \
    --gin_bindings="Config.data_dir = '${DATA_DIR}'" \
    --gin_bindings="Config.exp_name = '${EXP_NAME}'" \
    --gin_bindings="Config.factor = 4"

# or you can also run without accelerate (without DDP)
CUDA_VISIBLE_DEVICES=0 python train.py \
    --gin_configs=configs/360.gin \
    --gin_bindings="Config.data_dir = '${DATA_DIR}'" \
    --gin_bindings="Config.exp_name = '${EXP_NAME}'" \
      --gin_bindings="Config.factor = 4" 

# alternatively you can use an example training script 
bash scripts/train_360.sh

# blender dataset
bash scripts/train_blender.sh

# metric, render image, etc can be viewed through tensorboard
tensorboard --logdir "exp/${EXP_NAME}" 

autoDl:
tensorboard --logdir "exp/${EXP_NAME}" --port 6007
lsof -i:6007
    kill -7 PID
ps -ef | grep tensorboard | awk '{print $2}' | xargs kill -9

• Render video

accelerate launch render.py \
    --gin_configs=configs/360.gin \
    --gin_bindings="Config.data_dir = '${DATA_DIR}'" \
    --gin_bindings="Config.exp_name = '${EXP_NAME}'" \
    --gin_bindings="Config.render_path = True" \
    --gin_bindings="Config.render_path_frames = 480" \
    --gin_bindings="Config.render_video_fps = 60" \
    --gin_bindings="Config.factor = 4"  

# alternatively you can use an example rendering script 
bash scripts/render_360.sh

• Evaluate

# using the same exp_name as in training
accelerate launch eval.py \
    --gin_configs=configs/360.gin \
    --gin_bindings="Config.data_dir = '${DATA_DIR}'" \
    --gin_bindings="Config.exp_name = '${EXP_NAME}'" \
    --gin_bindings="Config.factor = 4"


# alternatively you can use an example evaluating script 
bash scripts/eval_360.sh

• Extract mesh

# more configuration can be found in internal/configs.py
accelerate launch extract.py \
    --gin_configs=configs/360.gin \
    --gin_bindings="Config.data_dir = '${DATA_DIR}'" \
    --gin_bindings="Config.exp_name = '${EXP_NAME}'" \
    --gin_bindings="Config.factor = 4"
#    --gin_bindings="Config.mesh_radius = 1"  # (optional) smaller for more details e.g. 0.2 in bicycle scene
#    --gin_bindings="Config.isosurface_threshold = 20"  # (optional) empirical value
#    --gin_bindings="Config.mesh_voxels=134217728"  # (optional) number of voxels used to extract mesh, e.g. 134217728 equals to 512**3 . Smaller values may solve OutoFMemoryError
#    --gin_bindings="Config.vertex_color = True"  # (optional) saving mesh with vertex color instead of atlas which is much slower but with more details.
#    --gin_bindings="Config.vertex_projection = True"  # (optional) use projection for vertex color

# or extracting mesh using tsdf method
accelerate launch tsdf.py \
    --gin_configs=configs/360.gin \
    --gin_bindings="Config.data_dir = '${DATA_DIR}'" \
    --gin_bindings="Config.exp_name = '${EXP_NAME}'" \
    --gin_bindings="Config.factor = 4"

# alternatively you can use an example script 
bash scripts/extract_360.sh