Mip-NeRF 360

Title	Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields
Author	Jonathan T. Barron Ben Mildenhall Dor Verbin Pratul P. Srinivasan Peter Hedman
Conf/Jour	CVPR 2022 (Oral Presentation)
Year	2022
Project	mip-NeRF 360 (jonbarron.info)
Paper	Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields (readpaper.com)

• novel Kalman-like scene parameterization：将场景参数化，将单位球外背景采样的截头锥参数化到r=2的球体内，单位球内的截头锥不受影响

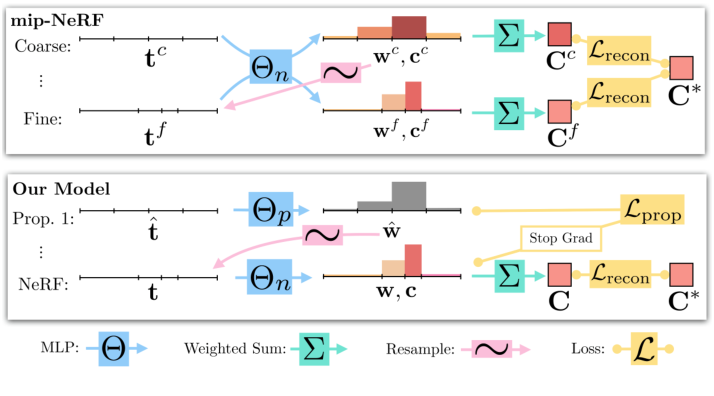
• efficient proposal-based coarse-to-fine distillation framework：一个提议网络用来获取权重，用来进行精采样，再通过精采样的点根据NeRF 的MLP得到密度和颜色值

• regularizer designed for mipNeRF ray intervals：可以有效消除floaters(体积密集空间中不相连的小区域)和背景塌陷(远处的表面被错误地模拟成靠近相机的密集内容的半透明云)

$\begin{gathered}\mathcal{L}_{\mathrm{dist}}(\mathbf{s},\mathbf{w}) =\sum_{i,j}w_iw_j\left|\frac{s_i+s_{i+1}}{2}-\frac{s_j+s_{j+1}}{2}\right| \+\frac13\sum_iw_i^2(s_{i+1}-s_i) \end{gathered}$

DC

Limitations. Though mip-NeRF 360 significantly outperforms mip-NeRF and other prior work, it is not perfect.

• Some thin structures and fine details may be missed, such as the tire spokes轮胎辐条 in the bicycle scene (Figure 5), or the 树叶上纹理veins on the leaves in the stump scene (Figure 7).
• View synthesis quality will likely degrade if the camera is moved far from the center of the scene. And, like most NeRF-like models, recovering a scene requires several hours of training on an accelerator, precluding on-device training.

Conclusion
We have presented mip-NeRF 360, a mip-NeRF extension designed for real-world scenes with unconstrained camera orientations. Using a novel Kalman-like scene parameterization, an efficient proposal-based coarse-to-fine distillation framework, and a regularizer designed for mipNeRF ray intervals, we are able to synthesize realistic novel views and complex depth maps for challenging unbounded real-world scenes, with a 57% reduction in mean-squared error compared to mip-NeRF.

AIR

尽管神经辐射场(NeRF)在物体和小范围空间区域上展示了令人印象深刻的视图合成结果，但在“无界”场景上，它们很难实现，因为摄像机可能指向任何方向，内容可能存在于任何距离

在这种情况下，现有的类似nerf的模型经常产生模糊或低分辨率的渲染图(由于近处和远处物体的细节和比例不平衡)，训练速度慢，并且由于从一小组图像重建大场景的任务固有的模糊性，可能会exhibit artifacts

我们提出了mip-NeRF(一种解决采样和混叠的NeRF变体)的扩展，它使用非线性场景参数化、在线蒸馏和一种新的基于扭曲的正则化来克服无界场景带来的挑战

我们的模型，我们称之为“mip-NeRF 360”，因为我们的目标场景中，摄像机围绕一个点旋转360度，与mip-NeRF相比，减少了57%的平均误差，并且能够为高度复杂的、无限的现实场景生成逼真的合成视图和详细的深度图

Introduction

神经辐射场(NeRF)通过在基于坐标的多层感知器(MLP)的权重内编码场景的体积密度和颜色来合成高度逼真的场景渲染。这种方法在真实感视图合成方面取得了重大进展。然而，NeRF使用沿着光线的无限小的3D点对MLP的输入进行建模，这会导致在呈现不同分辨率的视图时产生混淆。Mip-NeRF解决了这个问题，将NeRF扩展到沿锥体[3]的体积截锥。虽然这提高了质量，但在处理无界场景时，NeRF和mip-NeRF都会遇到困难，因为相机可能面对任何方向，场景内容可能存在于任何距离。在这项工作中，我们提出了一个扩展到mip-NeRF，我们称之为“mip-NeRF 360”，能够产生这些无界场景的逼真渲染，如图1所示。

将类似nerf的模型应用于大型无界场景会引发三个关键问题:

• Parameterization.参数化：对于前景和背景的参数化处理。无界360度场景可以占据任意大的欧几里得空间区域，但mip-NeRF要求3D场景坐标位于有界域内。
  • 参数化。由于透视投影的原因，一个物体放置在远离相机的地方会占据图像平面的一小部分，但如果放置在离相机较近的地方，则会占据更多的图像，并且可以看到细节。因此，理想的3D场景参数化应该为附近的内容分配更多的容量，而为远处的内容分配更少的容量。
  • 在NeRF之外，传统的视图合成方法通过在投影全景空间中参数化场景来解决这个问题[2,4,9,16,23,27,36,46,54]，或者通过将场景内容嵌入到一些使用多视图立体恢复的代理几何中[17,26,41]。NeRF成功的一个方面是它将特定场景类型与适当的3D参数化相结合。最初的NeRF论文[33]专注于360度捕捉具有遮罩背景的物体，以及所有图像朝向大致相同方向的正面场景。对于被遮挡的物体，NeRF直接在三维欧几里德空间中参数化场景，但对于面向前方的场景（LLFF），NeRF使用在射影空间中定义的坐标(归一化设备坐标，或“NDC”[5])。通过将一个无限深的相机截锥体扭曲成一个有界的立方体，其中沿z轴的距离对应于视差(逆距离)，NDC有效地重新分配了NeRF MLP的容量，这种方式与透视投影的几何形状一致。
  • 然而，在所有方向上都是无界的场景，而不仅仅是在一个方向上，需要不同的参数化。nerf++[51]和DONeRF[34]探索了这一想法，nerf++[51]使用了一个额外的网络来模拟远处的物体，DONeRF[34]提出了一个空间扭曲过程，以缩小距离原点的点。这两种方法的行为在某种程度上类似于NDC，但在每个方向上，而不仅仅是沿着z轴。在这项工作中，我们将这一思想扩展到mip-NeRF，并提出了一种将任何平滑参数化应用于volumes(而不是点)的方法，也提出了我们自己的无界场景参数化。
• Efficiency.效率。大型和详细的场景需要更多的网络容量，但是在训练期间沿着每条射线密集地查询大型MLP是昂贵的。
  • 处理无界场景的一个基本挑战是，这样的场景通常很大，而且细节很详细。虽然类似NeRF的模型可以使用令人惊讶的少量权重准确地再现场景的对象或区域，但当面对日益复杂的场景内容时，NeRF MLP的容量会饱和。此外，更大的场景需要沿着每条射线进行更多的样本来精确地定位表面。例如，当将NeRF从物体缩放到建筑物时，MartinBrualla et al.[30]将MLP隐藏单元的数量增加了一倍，并将MLP评估的数量增加了8倍。这种模型容量的增加是昂贵的- NeRF已经需要几个小时来训练，并且将这个时间乘以额外的~ 40×对于大多数用途来说是非常缓慢的。
  • NeRF和mip-NeRF使用的从粗到细的重采样策略加剧了这种训练成本:mlp使用“粗”和“细”射线间隔多次评估，并使用两次的图像重建损失进行监督。这种方法是浪费的，因为场景的“粗糙”渲染对最终图像没有贡献。我们将训练两个MLP:一个“提案MLP”和一个“NeRF MLP”，而不是训练一个在多个尺度上监督的NeRF MLP。The proposal MLP预测体积密度(但不是颜色)，这些密度用于重新采样提供给NeRF MLP的新间隔，然后渲染图像。至关重要的是，提议的MLP产生的权重不是使用输入图像进行监督，而是使用NeRF MLP生成的直方图权重进行监督。这允许我们使用评估次数相对较少的大型NeRF MLP，以及评估次数较多的小型提案MLP。因此，我们的整个模型的总容量明显大于mip-NeRF的(~ 15倍)，从而大大提高了渲染质量，但我们的训练时间仅略微增加(~ 2倍)。
  • 我们可以把这种方法看作是一种“在线蒸馏”:“蒸馏”通常指的是训练一个小网络来匹配一个已经训练好的大网络的输出[19]，在这里，我们通过同时训练两个网络，将NeRF MLP预测的输出结构提炼成“在线”的提议MLP。NeRV[47]对一个完全不同的任务执行类似的在线蒸馏:训练mlp近似渲染积分，以建模可见性和间接照明。我们的在线蒸馏方法在精神上类似于DONeRF中使用的“抽样oracle网络”，尽管该方法使用ground-truth深度进行监督[34]。在TermiNeRF[39]中使用了一个相关的想法，尽管这种方法只会加速推理，实际上会减慢训练速度(NeRF被训练到收敛，然后再训练一个额外的模型)。在NeRF中详细探讨了一个学习的“提议者”网络[1]，但只实现了25%的加速，而我们的方法将训练加速了300%。
  • 一些作品试图将训练好的NeRF提取或“烘烤”成可以快速呈现的格式[18,40,50]，但这些技术并不能加速训练。通过八阶数据结构(如八阶树[43]或包围体层次[42])加速光线跟踪的想法在渲染文献中得到了很好的探索，尽管这些方法假设了场景几何的先验知识，因此不能自然地推广到逆向渲染上下文，其中场景几何是未知的，必须恢复。事实上，尽管在优化类nerf模型的同时构建了一个八叉树加速结构，神经稀疏体素场方法并没有显著减少训练时间[28]。(只是提高了推理效率，而没有提高训练效率)
• Ambiguity.歧义。无界场景的内容可能位于任何距离，只会被少量光线观察到，这加剧了从2D图像重建3D内容的固有模糊性。
  • 虽然NeRF传统上是使用场景的许多输入图像进行优化的，但从新的相机角度恢复NeRF以产生逼真的合成视图的问题仍然从根本上受到限制-an infinite family of NeRFs可以解释输入图像，但只有一小部分可以产生可接受的新视图结果。例如，NeRF可以通过简单地在其各自的相机前将每个图像重建为纹理平面来重建所有输入图像。原始的NeRF论文通过在整流器之前向NeRF MLP的密度头注入高斯噪声来正则化模糊场景[33]，这促使密度向零或无穷大方向倾斜。虽然这通过阻止半透明密度减少了一些“漂浮物”，但我们将表明，这对于我们更具挑战性的任务是不够的。NeRF的其他正则化器已经被提出，例如密度上的鲁棒损失[18]或表面上的平滑惩罚[35,53]，但这些解决方案解决的问题与我们的不同(分别是渲染缓慢和表面不光滑)。此外，这些正则化器是为NeRF使用的点样本设计的，而我们的方法是为了处理沿着每个mip-NeRF射线定义的连续权重。
  • 我们将使用一个由具有挑战性的室内和室外场景组成的新数据集来展示我们对先前工作的改进。我们敦促读者观看我们的补充视频，因为我们的结果是最好的欣赏动画。

Preliminaries: mip-NeRF

mip-NeRF：通过将光线分成一组间隔$T_{i} = [t_{i}, t_{i+1}]$，对于每个区间，计算对应于该区间的圆锥截体的均值和协方差（将圆锥截体近似为高阶高斯分布函数），圆锥截体的半径由射线的焦距和图像平面上的像素大小决定

使用集成位置编码来表征这些值:
$\gamma(\mathbf{\mu},\mathbf{\Sigma})=\left\{\begin{bmatrix}\sin(2^\ell\mathbf{\mu})\exp\left(-2^{2\ell-1}\operatorname{diag}(\mathbf{\Sigma})\right)\\\cos(2^\ell\mathbf{\mu})\exp\left(-2^{2\ell-1}\operatorname{diag}(\mathbf{\Sigma})\right)\end{bmatrix}\right\}_{\ell=0}^{L-1}$

经过MLP得到密度和颜色：$\forall T_i\in\mathrm{t},\quad(\tau_i,\mathbf{c}_i)=\mathrm{MLP}(\gamma(\mathbf{r}(T_i));\Theta_\mathrm{NeRF}).$

使用体渲染函数，根据权重计算像素的颜色值：

$\begin{gathered}\mathbf{C}(\mathbf{r},\mathbf{t})=\sum_iw_i\mathbf{c}_i,\\w_i=\left(1-e^{-\tau_i(t_{i+1}-t_i)}\right)e^{-\sum_{i’<i}\tau_{i’}\left(t_{i’+1}-t_{i’}\right)}\end{gathered}$

• 采样方式：

  • 粗采样：均匀采样$t^c\sim\mathcal{U}[t_n,t_f],\quad\mathbf{t}^c=\operatorname{sort}(\{t^c\}).$
  • 精采样：$t^f\sim\operatorname{hist}(\mathbf{t}^c,\mathbf{w}^c),\quad\mathbf{t}^f=\operatorname{sort}(\{t^f\}).$

• loss：$\sum_{\mathrm{r}\in\mathcal{R}}\frac{1}{10}\mathcal{L}_{\mathrm{recon}}(\mathbf{C}(\mathbf{r},\mathbf{t}^{c}),\mathbf{C}^{}(\mathbf{r}))+\mathcal{L}_{\mathrm{recon}}(\mathbf{C}(\mathbf{r},\mathbf{t}^{f}),\mathbf{C}^{}(\mathbf{r}))$

  • recon: mean squared error.
  • R为光线几何
  • $C^{*}$为ground truth

Scene and Ray Parameterization

重新参数化高斯函数

定义一个f(x): $\mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ 映射的平滑坐标变换(n=3)

compute the linear approximation: $f(\mathbf{x})\approx f(\mathbf\mu)+\mathbf{J}_f(\mathbf\mu)(\mathbf{x}-\mathbf\mu)$

$\mathbf{J}_f(\boldsymbol\mu)$为f at $\mu$的雅克比矩阵，即对均值和方差：$f(\mu,\Sigma)=\begin{pmatrix}f(\mu),\mathbf{J}_f(\mu)\Sigma\mathbf{J}_f(\mu)^\mathrm{T}\end{pmatrix}$

这在功能上等价于经典的扩展卡尔曼滤波器[21]，其中f是状态转移模型。我们对f的选择是如下的缩略式:
$\operatorname{contract}(\mathbf{x})=\begin{cases}\mathbf{x}&|\mathbf{x}|\leq1\\\left(2-\frac{1}{|\mathbf{x}|}\right)\left(\frac{\mathbf{x}}{|\mathbf{x}|}\right)&|\mathbf{x}|>1\end{cases}$
这种设计与NDC的动机相同:距离点应该按视差(逆距离)而不是距离成比例分布

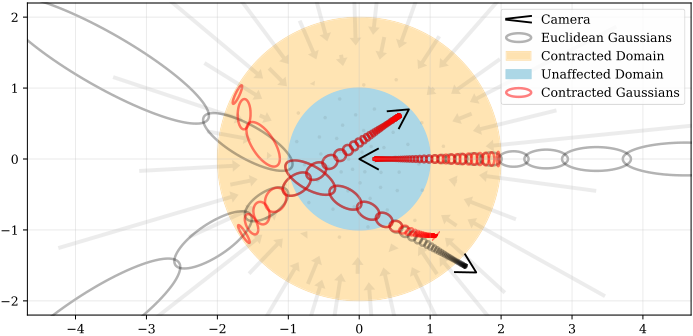
在我们的模型中，我们不是按照公式1在欧几里得空间中使用mip-NeRF的IPE特征，而是在这个收缩空间中使用类似的特征(见附录):γ(contract(μ， Σ))。图2显示了该参数化。

我们的场景参数化的2D可视化。我们定义了一个contract(·)操作符(公式10，如箭头所示)，它将坐标映射到一个半径为2(橙色)的球上，其中半径为1(蓝色)内的点不受影响。我们将这种收缩应用于欧几里得3D空间中的mip-NeRF高斯函数(灰色椭圆)，类似于卡尔曼滤波器，以产生我们的收缩高斯函数(红色椭圆)，其中心保证位于半径为2的球内。contract(·)的设计结合我们根据视差线性选择空间射线间隔，意味着从位于场景原点的摄像机投射的射线在橙色区域具有等距间隔，如图所示。

如何选择ray距离

除了如何参数化3D坐标的问题，还有如何选择射线距离的问题。在NeRF中，这通常是通过从近平面和远平面均匀采样来完成的，如公式5所示。然而，如果使用NDC参数化，这个等间距的样本系列实际上是均匀间隔的反深度(视差)。这种设计决策非常适合于当相机只面向一个方向时的无界场景，但不适用于所有方向都无界的场景。因此，我们将显式地以视差线性采样距离t(参见[PDF] Local Light Field Fusion: Practical View Synthesis with Prescriptive Sampling Guidelines-论文阅读讨论-ReadPaper了解此间距的详细动机)。

为了根据视差参数化射线，我们定义了欧氏射线距离t和“标准化”射线距离之间的可逆映射$s\triangleq\frac{g(t)-g(t_n)}{g(t_f)-g(t_n)},t\triangleq g^{-1}(s\cdot g(t_f)+(1-s)\cdot g(t_n)),$

• 其中g(·)是可逆标量函数。这给了我们“标准化”的射线距离s∈[0,1]，映射到[tn, tf]。在本文中，我们将参考沿t空间或s空间的射线的距离，这取决于哪个更方便或直观。
• 通过设置g(x) = 1/x并构造均匀分布在空间中的射线样本，我们得到的射线样本的t-距离以视差线性分布(另外，设置g(x) = log(x)产生DONeRF的对数间距[34])。
• 在我们的模型中，不是使用t个距离来执行粗精采样，而是使用s个距离来执行。这意味着，不仅我们的初始样本在视差上是线性间隔的，而且从权重w的各个间隔进行的后续重采样也将以类似的方式分布。从图2中心的摄像机可以看出，射线样本的线性视差间距抵消了contract(·)。实际上，我们已经用反向深度间距共同设计了我们的场景坐标空间，这给了我们无界场景的参数化，这与原始NeRF论文的高效设置非常相似:有界空间中均匀间隔的射线间隔。

Coarse-to-Fine Online Distillation

如前所述，mip-NeRF使用了一种从粗到细的重采样策略(图3)，其中使用“粗”射线间隔和“细”射线间隔对MLP进行一次评估，并使用两个级别的图像重建损失进行监督。

我们转而训练两个MLP，一个“NeRF MLP”ΘNeRF(其行为类似于NeRF和mip-NeRF使用的MLP)和一个“提议MLP”Θprop。提案MLP预测体积密度，根据公式4将其转换为提案权重向量，但不预测颜色。这些建议的权值用于采样s区间，然后提供给NeRF MLP, NeRF MLP预测自己的权值向量w(和颜色估计，用于渲染图像)。
至关重要的是，提议 MLP 没有经过训练来重现输入图像，而是经过训练以绑定 NeRF MLP 产生的权重 w。这两个 MLP 都是随机初始化和联合训练的，因此这种监督可以被认为是 NeRF MLP 知识的一种“在线蒸馏”到提议 MLP。我们使用大型 NeRF MLP 和小型提案 MLP，并从具有许多样本的提案 MLP 中反复评估和重新采样（为清楚起见，一些图形和讨论仅说明了单个重采样），但仅使用较小的样本集评估 NeRF MLP一次。这为我们提供了一种表现的模型，尽管它的容量比 mip-NeRF 高得多，但训练成本仅略高。正如我们将展示的那样，使用一个小的 MLP 来模拟提议分布不会降低准确性，这表明提取 NeRF MLP 比视图合成更容易的任务。

这种在线蒸馏需要一个损失函数，该函数鼓励提议的$MLP(\hat t, \hat w)$和NeRF MLP(t, w)发出的直方图保持一致。起初，这个问题可能看起来微不足道，因为最小化两个直方图之间的不相似性是一个很好的任务，但是回想一下，这些直方图t和t的“箱”不需要相似——事实上，如果提议的MLP成功地剔除了场景内容存在的距离集，t和$\hat t$将是高度不相似的。尽管文献中包含了许多测量具有相同箱位的两个直方图之间差异的方法[12,29,38]，但我们的研究相对较少。这个问题是具有挑战性的，因为我们不能假设内容在一个直方图bin内的分布:一个非零权重的区间可能表明权重在整个区间内的均匀分布，一个位于该区间内任何位置的函数，或者无数其他分布。因此，我们在以下假设下构建损失:

• 如果两个直方图都可以用任何单一的质量分布来解释，那么损失一定为零。只有当两个直方图不可能反映相同的“真实的”连续底层质量分布时，才会发生非零损失。请参阅附录以获得该概念的可视化。
• 要做到这一点，我们首先定义一个函数，计算与区间T重叠的所有建议权重的和:$\mathrm{bound}\big(\hat{\mathbf{t}},\hat{\mathbf{w}},T\big)=\sum_{j:T\cap\hat{T}_j\neq\emptyset}\hat{w}_j.$
• 如果两个直方图相互一致，则对于(t, w)中的所有区间$(T_{i}, w_{i})$，必须成立$w_{i}≤bound(\hat{\mathbf{t}},\hat{\mathbf{w}}, T_{i})$。这一性质类似于测度论[14]中外测度的可加性性质。我们的损失会惩罚任何违反这个不等式并超过这个界限的剩余直方图质量:
• $\mathcal{L}_{\mathrm{prop}}\big(\mathbf{t},\mathbf{w},\hat{\mathbf{t}},\hat{\mathbf{w}}\big)=\sum_i\frac{1}{w_i}\max\big(0,w_i-\mathrm{bound}\big(\hat{\mathbf{t}},\hat{\mathbf{w}},T_i\big)\big)^2$
• 这种损失类似于统计学和计算机视觉中经常使用的方形直方图距离的半二次型。这种损失是不对称的，因为我们只想惩罚那些低估了NeRF MLP所隐含的分布的提案权重——高估是意料之中的，因为提案权重可能比NeRF权重更粗糙，因此会在其上形成一个上限包络。除以$w_{i}$保证了当边界为零时，这个损失相对于边界的梯度是一个常数值，这导致了性能良好的优化。由于t和$\hat t$已排序，因此可以通过使用求和面积表[11]高效地计算公式13$\mathcal{L}_{prop}$。请注意，这种损失对于距离t的单调变换是不变的(假设w和$\hat w$已经在t空间中计算过)，所以无论应用于欧几里得射线距离还是标准化射线s距离，它的行为都是相同的。
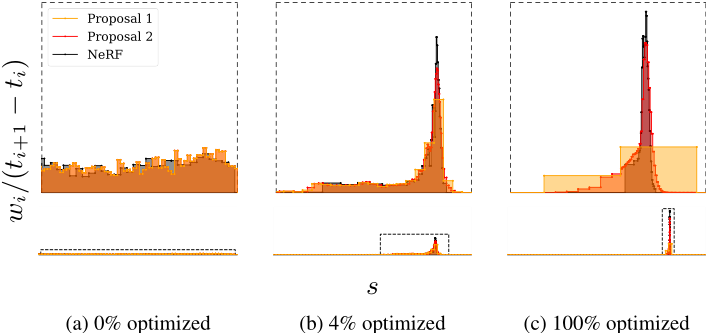
• 我们在NeRF直方图(t, w)和所有提案直方图$(\hat t^{k},\hat w^{k})$之间施加这种损失。与mip-NeRF一样，NeRF MLP使用带有输入图像$\mathcal{L}_{recon}$的重建损失进行监督。在计算$\mathcal{L}_{prop}$时，我们在NeRF MLP的输出t和w上放置一个停止梯度，使NeRF MLP“领先”，而提案MLP“跟随”-否则NeRF可能会产生更差的场景重建，从而使提案MLP的工作变得不那么困难。这种提议监督的效果可以从图4中看到，其中NeRF MLP逐渐将其权重w定位在场景中的一个表面周围，而提案MLP“catches up”并预测包含NeRF权重的粗提案直方图。

Regularization for Interval-Based Models

由于姿态不佳，训练有素的nerf经常表现出两种特征伪影，我们称之为“floaters”和“背景塌陷”，如图5(a)所示。我们所说的“floaters”指的是体积密集空间中不相连的小区域，它们可以解释输入视图子集的某些方面，但从另一个角度来看，它们看起来就像模糊的云。所谓“背景塌缩”，我们指的是一种现象，在这种现象中，远处的表面被错误地模拟成靠近相机的密集内容的半透明云。在这里，我们提出了一种正则化器，如图5所示，它比NeRF使用的向体积密度[33]注入噪声的方法更有效地防止浮动和背景崩溃。

我们的正则化器有一个简单的定义，它是由一组(标准化的)射线距离s和参数化每条射线的权重w定义的阶跃函数:
$\mathcal{L}_{\mathrm{dist}}(\mathbf{s},\mathbf{w})=\iint\limits_{-\infty}^\infty\mathbf{w}_\mathbf{s}(u)\mathbf{w}_\mathbf{s}(v)|u-v|d_ud_v,$
$\mathbf{w}_\mathbf{s}(u)=\sum_iw_i\mathbb{1}_{[s_i,s_{i+1})}(u).$

• 我们使用归一化射线距离s，因为使用t会显著提高远间隔的权重，并导致近间隔被有效忽略。这个损失是沿着这个1D阶跃函数的所有点对之间的距离的积分，由NeRF MLP分配给每个点的权重w缩放。我们称之为“失真”，因为它类似于k-means最小化失真的连续版本(尽管它也可以被认为是最大化一种自相关)。
• 这种损失可以通过设置w = 0来最小化(回想一下，w的总和不大于1，而不完全是1)。如果这是不可能的(即，如果射线是非空的)，则可以通过将权重合并到尽可能小的区域来最小化。图6通过在toy直方图上显示这种损失的梯度来说明这种行为。

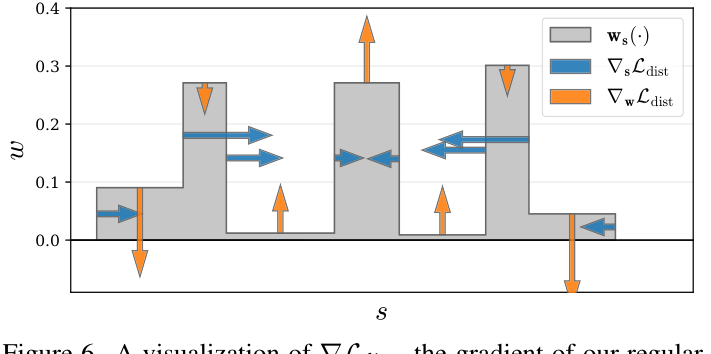
我们的损失鼓励每条射线尽可能紧凑:
1)最小化每个间隔的宽度，
2)将距离较远的间隔相互拉近，
3)将权重整合到单个间隔或少量邻近的间隔中，
4)在可能的情况下(例如当整个射线未被占用时)使所有权重趋近于零。

由于ws(·)在每个区间内都有一个常数值，我们可以将式14重写为:

$$\begin{gathered}\mathcal{L}_{\mathrm{dist}}(\mathbf{s},\mathbf{w}) =\sum_{i,j}w_iw_j\left|\frac{s_i+s_{i+1}}{2}-\frac{s_j+s_{j+1}}{2}\right| \\+\frac13\sum_iw_i^2(s_{i+1}-s_i) \end{gathered}$$

在这种形式下，我们的失真损失是微不足道的计算。这种重新表述也为这种损失的行为提供了一些直观的理解:第一项最小化所有区间中点对之间的加权距离，第二项最小化每个单独区间的加权大小。

Optimization

我们使用具有4层和256个隐藏单元的提议MLP和具有8层和1024个隐藏单元的NeRF MLP，两者都使用ReLU内部激活和密度τ的softplus激活。

我们对提议的MLP进行两个阶段的评估和重新采样，每个阶段使用64个样本来生产$(\hat s^{0}, \hat w^{0})$ 和$(\hat s^{1}, \hat w^{1})$, 然后使用32个样本对NeRF MLP进行一个阶段的评估，以产生(s, w)。我们将以下损失最小化: $\mathcal{L}_{\text{recon}}(\mathbf{C}(\mathbf{t}),\mathbf{C}^*)+\lambda\mathcal{L}_{\text{dist}}(\mathbf{s},\mathbf{w})+\sum_{k=0}^1\mathcal{L}_{\text{prop}}(\mathbf{s},\mathbf{w},\hat{\mathbf{s}}^k,\hat{\mathbf{w}}^k)$ 每批中所有光线的平均值(光线不包括在我们的符号中)

λ超参数平衡了我们的数据项$\mathcal{L}_{recon}$和正则器$\mathcal{L}_{dist}$;所有实验均设λ = 0.01。$\mathcal{L}_{prop}$中使用的停止梯度使Θprop的优化独立于ΘNeRF的优化，因此不需要超参数来缩放$\mathcal{L}_{prop}$的效果。对于$\mathcal{L}_{recon}$，我们使用Charbonnier loss[10] :$\sqrt{(x−x^{∗})^{2} + \epsilon^{2}} ,\epsilon= 0.001$，这比mip-NeRF中使用的均方误差实现了稍微稳定的优化。我们使用稍微修改过的mip-NeRF学习时间表来训练我们的模型(以及所有报告的类似nerf的基线):使用Adam[24]，使用超参数$β_{1} = 0.9， β_{2} = 0.999， \epsilon = 10^{−6}$，进行250k次优化迭代，批大小为214，学习率从$2 × 10^{−3}$到$2 × 10^{−5}$对数线性退火，预热阶段为512次迭代，梯度裁剪为$10^{−3}$范数。

Result

我们在一个新的数据集上评估我们的模型:9个场景(5个室外和4个室内)，每个场景都包含一个复杂的中心物体或区域和详细的背景。在拍摄过程中，我们试图通过固定相机曝光设置，最小化照明变化，避免移动物体来防止光度变化-我们不打算探索“在野外”照片收集[30]所带来的所有挑战，只有比例。相机姿势估计使用COLMAP[45]

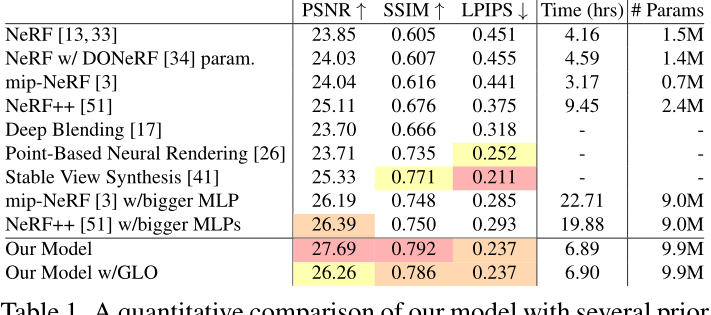
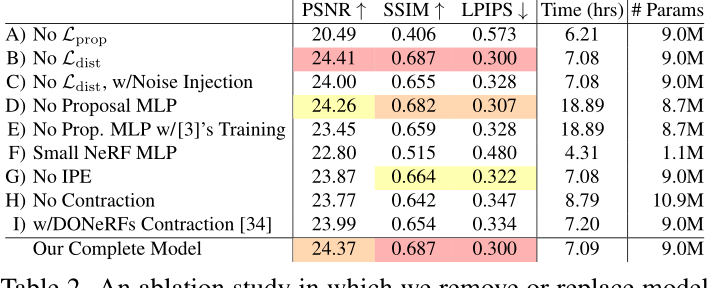
消融研究