QiYun

Note

NeRF++

Posted on Edited on In
2.4k 9 mins.
Title NeRF++: Analyzing and Improving Neural Radiance Fields
Author Kai Zhang, Gernot Riegler, Noah Snavely, Vladlen Koltun
Conf/Jour arXiv: Computer Vision and Pattern Recognition
Year 2020
Project Kai-46/nerfplusplus: improves over nerf in 360 capture of unbounded scenes (github.com)
Paper NeRF++: Analyzing and Improving Neural Radiance Fields. (readpaper.com)
arxiv.org/pdf/2010.07492

image.png

创新：一种前背景分离的方法
挑战：

  • First, the training and testing of NeRF and NeRF++ on a single large-scale scene is quite time-consuming and memory-intensive —> NGP解决了耗时
  • Second, small camera calibration errors may impede阻碍 photorealistic synthesis. Robust loss functions, such as the contextual loss (Mechrez et al., 2018), could be applied.
  • Third, photometric effects such as auto-exposure and vignetting渐晕 can also be taken into account to increase image fidelity. This line of investigation is related to the lighting changes addressed in the orthogonal work of Martin-Brualla et al. (2020).

AIR

We first remark on radiance fields and their potential ambiguities, namely the shape-radiance ambiguity, and analyze NeRF’s success in avoiding such ambiguities. Second, we address a parametrization issue involved in applying NeRF to 360◦ captures of objects within large-scale, unbounded 3D scenes

  • inverted sphere parameterization
    In this technical report, we first present an analysis of potential failure modes in NeRF, and an analysis of why NeRF avoids these failure modes in practice. Second, we present a novel spatial parameterization scheme that we call inverted sphere parameterization that allows NeRF to work on a new class of captures of unbounded scenes.

Why NeRF success: 利用了亮度与观察方向相关的不对称MLP解决了shape-radiance ambiguity
In particular, we find that in theory, optimizing the 5D function from a set of training images can encounter critical degenerate solutions that fail to generalize to novel test views, in the absence of any regularization. Such phenomena are encapsulated封装 in the shape-radiance ambiguity (Figure 1, left), wherein one can fit a set of training images perfectly for an arbitrary incorrect geometry by a suitable choice of outgoing 2D radiance at each surface point. We empirically show that the specific MLP structure used in NeRF plays an important role in avoiding such ambiguities, yielding an impressive ability to synthesize novel views. Our analysis offers a new view into NeRF’s impressive success.

a spatial parameterization issue: 对于360度拍摄的图片，可以有两种参数化的方法

  • 对整个空间参数化，前背景融合进行建模，但由于分辨率有限而缺乏细节
  • 只对前景物体即整个场景中的一个bound进行采样，这样会丢失掉背景元素

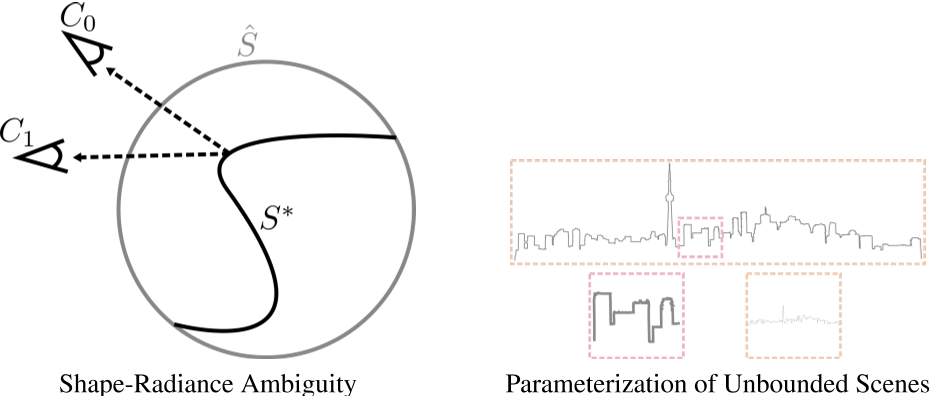
image.png

  • Shape-radiance ambiguity (left) and parameterization of unbounded scenes (right).
    • Shaperadiance ambiguity: our theoretical analysis shows that, in the absence of explicit or implicit regularization, a set of training images can be fit independently of the recovered geometry (e.g., for incorrect scene geometry $\hat S$ rather than correct geometry $S^{∗}$) by exploiting view-dependent radiance to simulate the effect of the correct geometry.
    • Parameterization of unbounded scenes:with standard parameterization schemes, either (1) only a portion of the scene is modeled (red outline), leading to significant artifacts in background elements, or (2) the full scene is modeled (orange outline), which leads to an overall loss of details due to finite sampling resolution

In summary, we present an analysis on how NeRF manages to resolve the shape-radiance ambiguity, as well as a remedy for the parameterization of unbounded scenes in the case of 360◦ captures.

PRELIMINARIES: NeRF

SHAPE-RADIANCE AMBIGUITY

The capacity of NeRF to model view-dependent appearance leads to an inherent ambiguity between 3D shape and radiance that can admit degenerate solutions, in the absence of regularization. For an arbitrary, incorrect shape, one can show that there exists a family of radiance fields that perfectly explains the training images, but that generalizes poorly to novel test views.

  • 对于一个特定的场景，可以找到一组辐射场，完美解释训练图像，但在测试视图上的泛化性很差
    • 根据训练集训练出来的radiance field 可以看成一个球，形状与真实物体完全不同，但是在训练view上渲染出来的图像却与真实的图片相差很小，当改变很小的view时即使用一个不同于训练集的view时，图片发生很大的变化
  • 对于一个简单的几何物体，需要很复杂的radiance field来进行表示。ref : NeRF++论文部分解读 为何NeRF如此强大？ - 知乎 (zhihu.com)
    • 想一想这个问题，NeRF会把一个镜子重建成一个平面还是一个有深度的几何（类似镜像的世界）？答案是会重建出几何，而不是一个镜子平面

将单位圆的opacity设置为1，其他设置为0，在训练集上训练得出的结果：
image.png

Why does NeRF avoid such degenerate solutions? We hypothesize that two related factors come to NeRF’s rescue:
1) incorrect geometry forces the radiance field to have higher intrinsic complexity (i.e., much higher frequencies) while in contrast
2) NeRF’s specific MLP structure implicitly encodes a smooth BRDF prior on surface reflectance.

  • As σ deviates from the correct shape, c must in general become a high-frequency function with respect to d to reconstruct the input images. For the correct shape, the surface light field will generally be much smoother (in fact, constant for Lambertian materials). The higher complexity required for incorrect shapes is more difficult to represent with a limited capacity MLP.
    • incorrect shape —> complex c(surface light field)
    • correct shape —> smoother surface light field
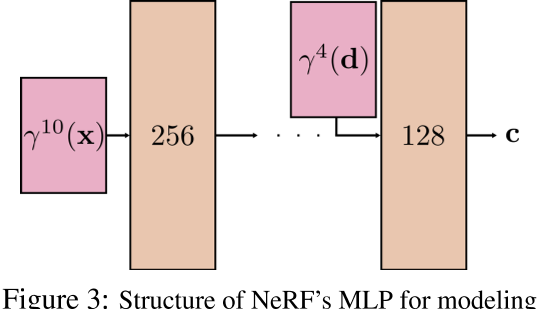
  • In particular, NeRF’s specific MLP structure encodes an implicit prior favoring smooth surface reflectance functions where c is smooth with respect to d at any given surface point x. This MLP structure, shown in Figure 3, treats the scene position x and the viewing direction d asymmetrically不对称的: d is injected into the network close to the end of the MLP, meaning that there are fewer MLP parameters, as well as fewer non-linear activations, involved in the creation of view-dependent effects. In addition, the Fourier features used to encode the viewing direction consist only of low-frequency components, i.e，对于位置x，频率编码为$\gamma^{10}(\cdot)$, 而对于方向d，频率编码仅有$\gamma^{4}(\cdot)$。In other words, for a fixed x, the radiance c(x, d) has limited expressivity with respect to d.
    • NeRF的MLP采用了不对称结构，方向d在MLP中只有少量的参数

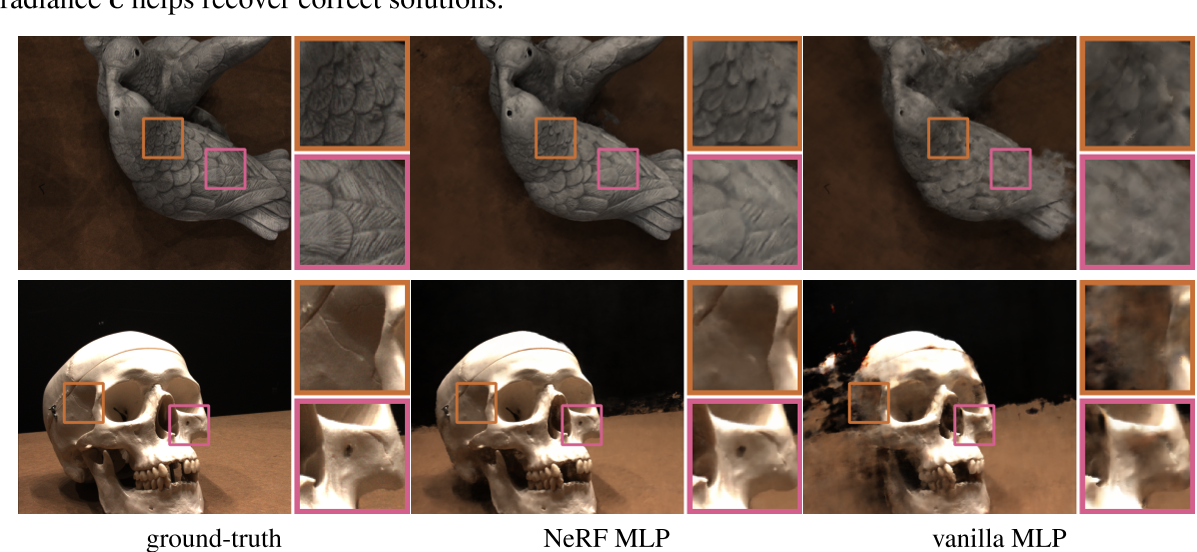
image.png

验证实验：

  • NeRF MLP
  • vanilla MLP : 对x和d 都进行$\gamma^{10}(\cdot)$编码，并同时输入进MLP网络

This result is consistent with our hypothesis that implicit regularization of reflectance in NeRF’s MLP model of radiance c helps recover correct solutions

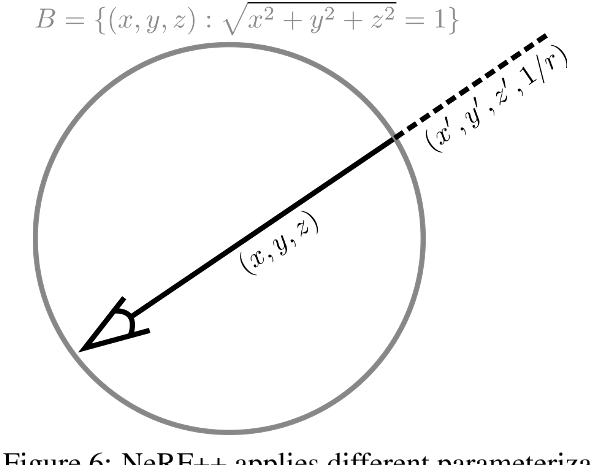
image.png

INVERTED SPHERE PARAMETRIZATION

NeRF的NDC操作虽然解决了无限远的问题，但是对360度环绕拍摄的场景无法很好的处理远处背景

  • 如果bound前景物体，对背景的重建效果很差
  • 如果bound整个场景，对物体的重建效果就会下降

image.png

将整个场景分成两个部分
partition the scene space into two volumes

  • an inner unit sphere前景：处于一个单位圆中
    • The inner volume contains the foreground and all the cameras, while the outer volume contains the remainder of the environment.
  • an outer volume represented by an inverted sphere covering the complement of the inner volume 背景：位置坐标由一个四维的向量表示，inverted sphere parameterization
    • the outer volume contains the remainder of the environment.

image.png

These two volumes are modelled with two separate NeRFs. To render the color for a ray, they are raycast individually, followed by a final compositition.

  • No re-parameterization is needed for the inner NeRF, as that part of the scene is nicely bounded.
  • For the outer NeRF, we apply an inverted sphere parametrization.

内部：(x, y, z)
外部：(x, y, z)需要参数化为$(x’,y’,z’,1/r)$ ，其中$x’^{2}+ y’^{2}+z’^{2}= 1$ ，(x’,y’,z’)，为与(x,y,z)同一条光线的单位方向向量，representing a direction on the sphere.

  • $r = \sqrt{x^2+y^2+z^2}>1$，所以 0 < 1/r < 1
  • i.e. 该点的坐标为 $r \cdot (x’,y’,z’) = (x,y,z)$
  • 重参数化后的参数都是有界的，0 < 1/r < 1，$x’,y’,z’ \in [-1,1]$

在光线$ray = o + td$中，相当于t被单位球分为两部分：

  • inside: $t \in [0,t’]$
  • outside: $t \in [t’,\infty]$

Terms (i) and (ii) are computed in Euclidean space, while term (iii) is computed in inverted sphere space with 1r as the integration variable.
In other words, we use $σ_{in}(o + td)$, $c_{in} (o + td, d)$ in terms (i) and (ii), and $σ_{out}(x′, y′, z′, 1/r)$, $c_{out} (x′, y′, z′, 1/r, d)$ in term (iii)

In order to compute term (iii) for the ray $r = o + td$, we first need to be able to evaluate $σ_{out}$ , $c_{out}$ at any 1/r; in other words, we need a way to compute (x′, y′, z′) corresponding to a given 1/r, so that $σ_{out}$, $c_{out}$ can take (x′, y′, z′, 1/r) as input..

about inverted sphere parameterization · Issue #19 · Kai-46/nerfplusplus (github.com)
为什么不直接用xyz除以r得到x’y’z’:

  • xyz有时太大，数值误差
  • 在代码中，计算xyz需要使用o和d，一般xyz是未知的，而r很好求得，因此使用这种方法
    • bg_depth = torch.linspace(0., 1., N_samples).view([1, ] * len(dots_sh) + [N_samples,]).expand(dots_sh + [N_samples,]).to(rank)
    • bg_depth 即 1/r

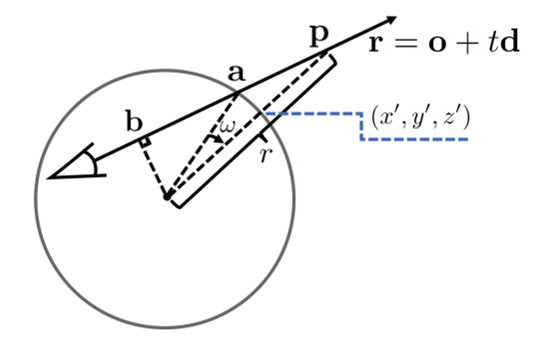
image.png
(x’,y’,z’)可由a和$\omega$得到
由$a = o + t_{a}d$得到$t_{a}$，a的位置

1
2
3
4
5
6
7
8
9
10
11
12
13
"""
由： ||o+td|| = 1
||d||^2*t^2 + 2*(o.d)*t + ||o||^2-1 = 0
因此求ta的代码：
"""
def intersect_sphere(rays_o, rays_d):
    odotd = torch.sum(rays_o*rays_d, 1)
    d_norm_sq = torch.sum(rays_d**2, 1)
    o_norm_sq = torch.sum(rays_o**2, 1)
    determinant = odotd**2+(1-o_norm_sq)*d_norm_sq
    assert torch.all(determinant>=0), \
        'Not all your cameras are bounded by the unit sphere; please make sure the cameras are normalized properly!'
    return (torch.sqrt(determinant)-odotd)/d_norm_sq

由$b = o + t_{b}d$得到b的位置，$\mathbf{d}^T(\mathbf{o}+t_b\mathbf{d})=0.$

$\omega=\arcsin|\mathbf{b}|-\arcsin(|\mathbf{b}|\cdot\frac{1}{r}).$，根据a的位置和角度$\omega$即可求得x’y’z’
具体算法ref: 罗德里格旋转公式 - 维基百科，自由的百科全书 (wikipedia.org)

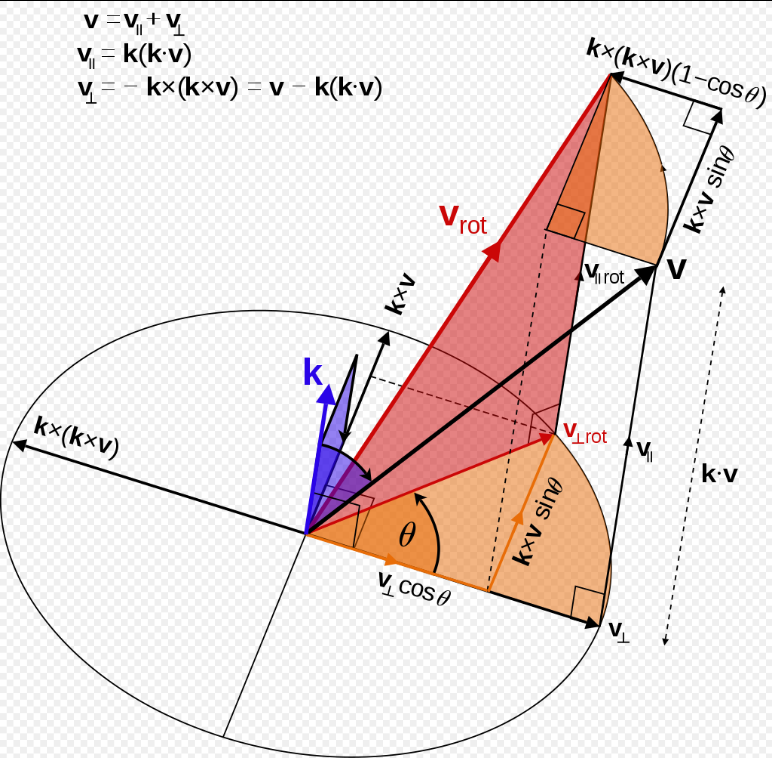
image.png|500

$\mathbf{v}_{\mathrm{rot}}=\mathbf{v}\cos\theta+(\mathbf{k}\times\mathbf{v})\sin\theta+\mathbf{k}(\mathbf{k}\cdot\mathbf{v})(1-\cos\theta).$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def depth2pts_outside(ray_o, ray_d, depth):
    '''
    ray_o, ray_d: [..., 3]
    depth: [...]; inverse of distance to sphere origin
    '''
    # note: d1 becomes negative if this mid point is behind camera
    d1 = -torch.sum(ray_d * ray_o, dim=-1) / torch.sum(ray_d * ray_d, dim=-1)
    p_mid = ray_o + d1.unsqueeze(-1) * ray_d
    p_mid_norm = torch.norm(p_mid, dim=-1)
    ray_d_cos = 1. / torch.norm(ray_d, dim=-1)
    d2 = torch.sqrt(1. - p_mid_norm * p_mid_norm) * ray_d_cos
    p_sphere = ray_o + (d1 + d2).unsqueeze(-1) * ray_d

    rot_axis = torch.cross(ray_o, p_sphere, dim=-1)
    rot_axis = rot_axis / torch.norm(rot_axis, dim=-1, keepdim=True)
    phi = torch.asin(p_mid_norm)
    theta = torch.asin(p_mid_norm * depth)  # depth is inside [0, 1]
    rot_angle = (phi - theta).unsqueeze(-1)     # [..., 1]

    # now rotate p_sphere
    # Rodrigues formula: https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula
    p_sphere_new = p_sphere * torch.cos(rot_angle) + \
                   torch.cross(rot_axis, p_sphere, dim=-1) * torch.sin(rot_angle) + \
                   rot_axis * torch.sum(rot_axis*p_sphere, dim=-1, keepdim=True) * (1.-torch.cos(rot_angle))
    p_sphere_new = p_sphere_new / torch.norm(p_sphere_new, dim=-1, keepdim=True)
    pts = torch.cat((p_sphere_new, depth.unsqueeze(-1)), dim=-1)

    # now calculate conventional depth
    depth_real = 1. / (depth + TINY_NUMBER) * torch.cos(theta) * ray_d_cos + d1
    return pts, depth_real

Welcome to my other publishing channels