| Title | Floaters No More: Radiance Field Gradient Scaling for Improved Near-Camera Training |
|---|---|
| Author | Julien Philip1, Valentin Deschaintre1 |
| Conf/Jour | The Eurographics Association |
| Year | 2023 |
| Project | Floaters No More: Radiance Field Gradient Scaling for Improved Near-Camera Training (gradient-scaling.github.io) |
| Paper | Floaters No More: Radiance Field Gradient Scaling for Improved Near-Camera Training (readpaper.com) |
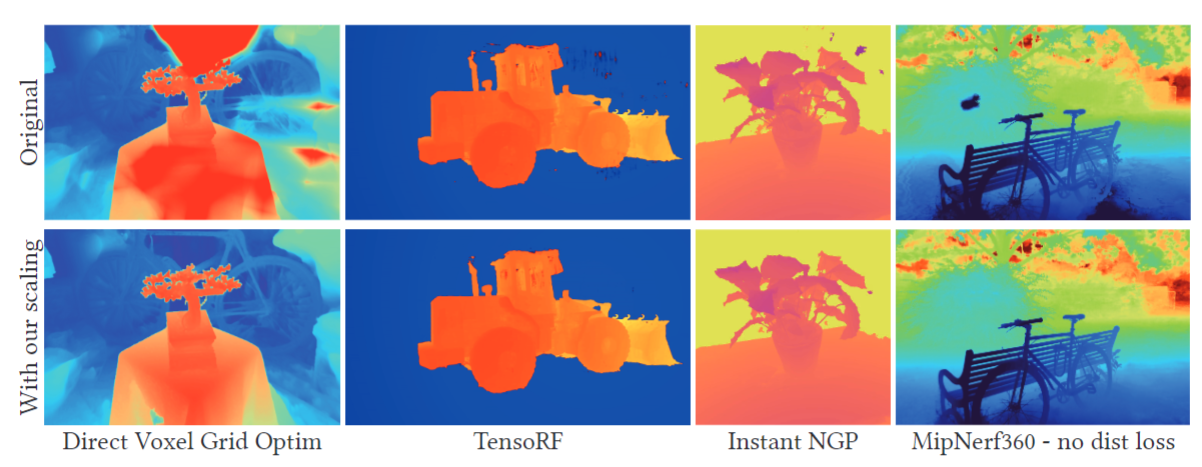
消除由近平面过度采样导致的摄像头附近漂浮物
可以通过几行代码简单的用于:
- Mip-NeRF 360
- InstantNGP
- DVGO
- TensoRF
Conclusion
我们提出了一种简单而有效的梯度缩放方法,在防止背景塌陷的同时,消除了NeRF类方法中对近平面设置的需要。
我们的方法计算效率高,解决了大多数已发表方法中存在的采样不平衡问题。这在物体距离相机任意近或距离不同的捕捉场景中尤为重要。我们的缩放直接适用于大多数类似NeRF的表示,并且可以很容易地与几行代码集成
AIR
NeRF采集通常需要仔细选择不同相机的近平面,否则会遭受背景崩溃,在捕获场景的边缘产生浮动伪影。这项工作的关键见解是,背景塌陷是由靠近相机的区域的高密度样本引起的。由于这种采样不平衡,近相机体积接收到更多的梯度,导致不正确的密度积累。我们提出了一种梯度缩放方法来平衡这种采样不平衡,消除了对近平面的需要,同时防止背景崩溃。我们的方法可以在几行代码中实现,不会产生任何显著的开销,并且与大多数NeRF实现兼容。
Introduction
神经辐射场(Neural Radiance Fields, NeRF) [MST 20]引入了一种新的方法,对给定一组多视图图像的真实捕获物体和场景进行3D重建和渲染。NeRF方法基于可微分的体积渲染,在体积的每个点上指导密度和辐射的存在或不存在。这种灵活的表示和令人印象深刻的重建质量激发了新的研究方向,在重建质量、重建速度、渲染速度、模型压缩或所需内存等方面改进了原始公式。*尽管如此,一些问题,特别是背景崩溃和浮动仍然存在于大多数方法的重建中,特别是对于真实场景,这指向了一个更根本的问题。在这项工作中,我们研究并提出了一个假设和一个简单的解决方案来解决背景崩溃和近相机漂浮物的问题。
背景塌缩症状是非常明显的浮动伪影,出现在训练摄像机附近,错误地将一些背景烤成前景密度。
- 先前的研究Mip-NeRF 360[BMV∗22]已经确定了这个问题,该研究在强迫密度集中并接近狄拉克[BMV∗22]的损失中增加了一个项来解决这个问题。虽然这个项确实减少了背景崩溃,但它并没有解释它,并且在优化中存在一些先验,这可能不适合所有场景。
- 另一个经常被掩盖的在减少背景塌缩中起作用的细节是在射线行进过程中使用近平面。它完全防止梯度反向传播到近相机区域,因为它们没有采样,但它是场景相关的,必须手动调整,并且在物理上是不准确的。此外,对于与被摄对象距离不同的复杂捕获,可能不存在良好的全景式近平面。
- 相反,我们认为任何NeRF方法都应该能够直接跟踪来自相机的光线,而不会导致背景塌陷或漂浮物,并且这种伪影的一个可能原因是近相机体积元素接收的梯度不成比例。因此,我们建议在反向传播期间缩放梯度,以使用非常简单的近似来补偿这种不平衡。这种缩放允许我们完全消除对近平面的需求,同时防止背景塌陷。
基于NeRF的方法主要在其底层体积数据结构上有所不同,这些数据结构可以简单到多层感知机[BMT∗21,BMV∗22,MST∗20],体素哈希网格[MESK22],张量分解[CXG∗22]甚至是普通体素[SSC22a]。我们表明,无论选择的数据结构如何,重构都受益于我们的梯度缩放方法。
贡献:
- 确定一个背景塌陷可能的根本原因:近相机区域梯度接收的不平衡。
- 提出一个轻量级的梯度缩放解决方案。
- 演示了它在具有广泛不同数据结构的几种方法中的有效性。
Related work
我们证明我们的方法对许多现有的NeRF [MST 20]相关方法是有益的。我们首先介绍基于辐射场的视图合成方法,然后进一步讨论辐射场文献中的背景塌陷和近相机采样问题,以及迄今为止如何解决这个问题。为了更详尽地了解最近快节奏的文献,我们推荐Tewari等人最近对神经渲染的调查Advances in Neural Rendering[TTM 22]。
NeRF representations
NeRF [MST * 20]为新视图合成引入了一种不同的表示。与依赖于预计算几何和重投影的基于网格的方法[OCDD15, HRDB16, HPP∗18,RK20, RK21,PMGD21]或基于点云的方法[ASK∗20,KPLD21, RALB22, KLR∗22]相反,辐射场通过可微射线推进和体绘制共同优化三维体积密度场和六维辐射场。这种方法经过调整,可以使用各种数据结构来存储底层字段,从而提供不同的质量、紧凑性、优化速度和呈现速度权衡。
- 最初的工作线[MST∗20,ZRSK20]使用mlp来表示场景,后来扩展到防止混叠[BMT∗21],处理无界场景[BMV∗22]并更好地表示反射[VHM∗22]。虽然这些方法提供了一些最高质量的结果,但它们的优化速度相对较慢,渲染速度也很慢,通常每帧需要几秒钟。
- 为了克服这些限制,一些作品在表示中重新引入了一些局部性,以避免对每个空间点评估一个大的MLP。KiloNeRF [RPLG21]提出先训练NeRF,然后再用微小的局部mlp再现优化后的场,从而加快渲染速度。以类似的精神,PlenOctrees [YLT 21]在训练原始NeRF后烘烤一个八叉树。Hedman等人提出烘烤[HSM 21]预训练的NeRF来提高渲染速度,然而,它并没有提高优化时间。
- 加速优化已被证明可以通过直接优化网格或基于体素的数据结构[STC∗22,SSC22a,SSC22b]。在这种快速优化的背景下,紧凑性也得到了改进,使用张量分解[CXG∗22]或散列体素[MESK22]和自定义CUDA内核来实现极快的优化和渲染。
我们表明,这种表示的选择与我们的贡献是正交的,并且我们的梯度缩放可以很容易地集成,通过对具有不同表示的突出方法进行评估来解决背景崩溃。
Floaters, Background collapse and Sampling
一些工作观察并提出了解决基于辐射场的方法中浮子和背景塌缩问题的方法。
- Roessle等人[RBM∗22]提出在稀疏捕获的背景下使用深度先验来解决这个问题,而在NeRFShop中,Jambon等人[JKK∗23]承认浮动的问题,并提出了一种编辑方法来去除它们。MipNeRF360 [BMV 22]提出了一种损耗,鼓励密度沿着射线集中在单个点周围,有效地减少近相机的半透明辐射。这种相对较大的损失进一步提高了效率[SSC22b]。NeRF in the Dark[MHMB 22]也建议减少权重方差以减少浮动。FreeNeRF [YPW23]详细讨论了这个问题,将其称为“墙壁”和“漂浮物”,注意到它们存在于相机附近,因此建议用遮挡损失来惩罚相机附近的密度。然而,使用这些损失会对场景密度分布施加先验,这可能不适合所有内容。此外,这些方法并不能解释这种现象的根本原因,也不能解释为什么密度在相机附近而不是在其他地方积聚。
在这项工作中,我们提供了一种可能的解释和解决方案,通过注意到近相机区域是过度采样的,因此接收到更强烈和更频繁的梯度。
Nimier-David等人[NDMKJ22]在体积效应优化(例如烟雾)的背景下发现了类似的采样问题,其中与透射率和密度的积成比例的采样导致密度累积斑块,而仅与透射率成比例的采样可显着减少伪影。
在我们的工作中,我们没有修改采样,而是考虑了它在反向传播步骤中的不平衡。
Analysis
在下一节中,我们简要回顾了辐射场优化(第3.1节),我们定义了问题(第3.2节),并提出了我们对该问题原因的假设(第3.3节)。
Neural Radiance Fields optimization
大多数NeRF方法共享共同的组件和假设,以优化其体积表示。从校准相机捕获的一组图像开始,目标是优化发射emissive体积密度,以便在使用分段恒定体积渲染渲染时再现输入图片的外观。一般优化框架在输入的训练图像中选择像素点,生成一条从摄像机出发,朝向所选像素点的射线,并沿着射线在离散位置对数据结构进行采样,从而进行射线行进,从而获得颜色和密度。这些样本的颜色和密度被整合,以获得通过该像素投射的每条光线的颜色。最后将这些颜色的聚合与原始像素值进行比较,导致使用随机梯度下降进行优化的损失。
Problem Statement
仅给定一组校准的输入图像,NeRF重建问题是不适定的,存在幼稚的解决方案。例如,靠近每个相机的一个平面,再现它们的图像内容,可能导致重建损失为0。在实践中,数据结构和损失正则器的性质部分地阻止了这种情况的发生。然而,一些人工制品经常保留下来:最突出的两个是漂浮物和一种被称为背景塌陷的现象,在这种现象中,一些几何形状在相机附近被重建。反过来,从其他角度来看,这种错误重建的几何形状被视为浮动几何形状。请注意,虽然背景塌陷会导致浮动,但一些浮动可能有不同的来源,我们的方法无法解决。
在图2中,我们用false颜色可视化深度图,从深蓝色(近)到红色(远)。我们可以在深度图中看到没有正则化器损失的深蓝色区域(a),表明在相机附近重建了一些几何形状。在MipNeRF360中,作者提出了一个相对复杂的loss $\mathcal{L}_{\mathrm{dist}}$,以部分解决浮动和背景塌陷问题——这些问题与近距离摄像机密度在其他视角下表现为浮动几何相关联。对于给定的射线,损失的目的是将样本权值合并到尽可能小的区域内
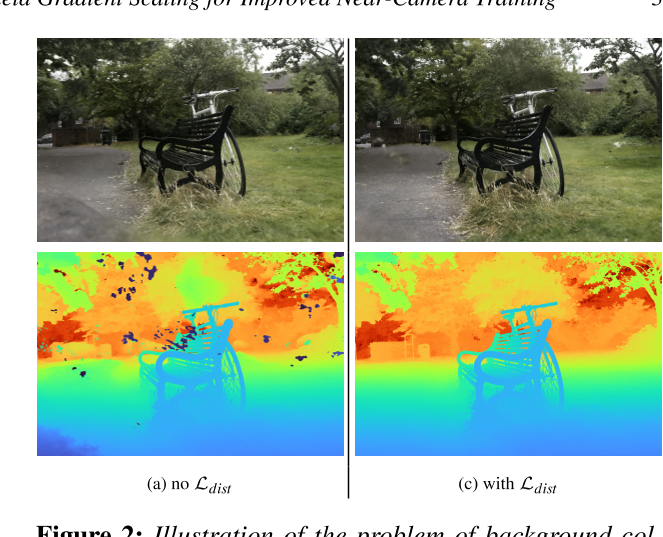
虽然这种损失部分地阻止了背景崩溃,但它并不能解释它。此外,它推动密度集中,这可能是一个问题,如果半透明的表面出现在场景中,因为它们是用部分密度表示的。
另一种减轻背景塌缩的简单方法是为superior 零的光线设置一个近平面,即光线不是从相机中心开始,而是从它有一定距离。实际上,这个技巧在大多数nerf相关的工作中都有使用,但很少讨论,也很少讨论它的含义。在优化像素时,使用非零近平面可防止任何梯度影响由相机中心和近平面形成的金字塔。另一方面,它防止在这个金字塔中重建和渲染,这意味着应该仔细选择近平面距离。如果它离相机太近,可能会出现背景塌陷,如果它太远,在重建过程中会丢失一些几何形状,并可能导致其他伪影。确实,当近平面位置过远时,模型必须在近平面之后用密度表示训练像素的颜色。虽然通常可以为近平面距离找到合理的值,但在一般情况下,它需要对每个场景进行调整。在从不同距离拍摄主体的情况下,这个近平面距离可能需要为每台相机独立设置。此外,当某些内容在离相机很近的地方被捕获时,可能就没有什么好的价值了。
Cause
我们假设背景塌缩主要是由接收到的近相机体积梯度不成比例引起的。如图3所示,来自相机的光线投射类似于光的传播,并且遭受类似的二次衰减。给定一个相机和一个可见的体积元素,并假设沿光线的采样间隔相等,则落在体积元素中的采样密度与到该相机的距离的平方的反比成正比。这意味着靠近相机的体积比它的其余部分采样更多,并且靠近相机的区域每个体积元素接收到更多的梯度,从而鼓励密度的快速建立,并创建浮动伪影。
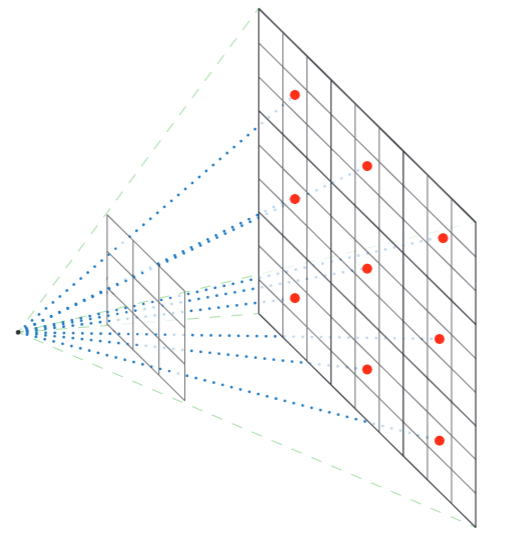
当光线从相机向场景传播时,采样点的密度降低:第一个矩形中所有区域都被采样,而第二个矩形(用红色圆圈标记)中$\frac{1}{9}$只有个采样点。
事实上,由于用于表示亮度场的数据结构通常是连续的,体积元素较高的采样率直接转化为用于表示体积的密度和颜色的变量的更强和更频繁的梯度。例如,在使用类体素结构[STC 22, MESK22, SSC22a, SSC22b]的半离散表示中,权值具有局部排列。在直接体素网格优化(DVGO) [SSC22a]和后续工作(DVGOv2) [SSC22b]中,只有与包含采样点的体素角相关的8个权重受到反向传递的影响。在这些情况下,更高的采样密度直接转化为更频繁地接收梯度,从而更快地更新。同样的推理也可以应用于NGP [MESK22]中不同级别的哈希网格。在类似MLP的隐式表示[MST∗20,BMT∗21,BMV∗22]的情况下,*更高的采样率意味着MLP在近相机空间接收到比其他地方更多的信号。
我们还注意到,当低频尚未拟合时,这种采样不平衡在训练早期具有最强的影响。在这个早期训练阶段,梯度可能在局部非常一致,因为它们都朝着同一个全局方向推进。例如,如果在早期迭代中预测的小体积的颜色在灰色周围变化,但目标是红色,则所有点都将获得近似相同的梯度以将颜色更改为更红。在这种情况下,这意味着影响体积元素的权重的梯度随该体积的采样密度线性缩放,并且权重变化得更快。
密度大的近相机部分,梯度应该进行缩小
Sampling in NeRF
给定一个针孔相机$c_i$,视点方向为$\vec{d}_i,$,对图像平面上的像素进行均匀采样。沿着这些射线,假设对点进行线性采样,则给定点p处的采样密度为:
- 其中$\nu_i(p)$是可见性函数(如果p在相机视场中,则为1,否则为0)。
- 第二项解释了边界上光线的空间密度较低
- 第三项解释了光线随距离的扩散。对于合理的相机视场,与距离衰减相比,第二项的影响可以忽略不计,我们可以近似地计算出$\frac{|p-c_i|}{\vec{d}_i\cdot(p-c_i)}\approx1$,得到:
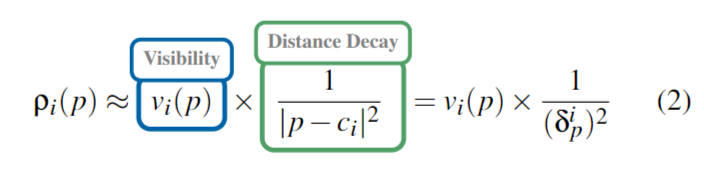
$\delta_{p}^i$ 是$c_i$与p之间的距离
对于有n个摄像机的完整场景,我们可以计算给定点p处的采样密度为所有摄像机的密度之和:$\mathsf{p}(p)\approx\sum_{i=0}^{n}\nu_{i}(p)\times\frac{1}{(\delta_{p}^{i})^{2}}$ Eq.3
由公式3中的总和给出的主要直觉是,对于一个点,可见且靠近给定的相机,总和由单个相机项主导,而对于距离相机较远且距离大致相等的点,可见性项起着重要作用。
- 对于靠近摄像机的点,距离的平方反比有非常显著的影响,而这些点往往只有少数摄像机可见。
- 另一方面,拍摄主体周围的点往往会被更多的相机看到。这种相机可见现象如图4a所示。
- 在图4b中,我们以对数尺度说明了沿相机光线的平均采样密度。我们可以看到,在相机附近,密度呈二次衰减,尽管能见度较低,但靠近相机的体积的采样密度不成比例,导致这些区域的梯度不成比例。
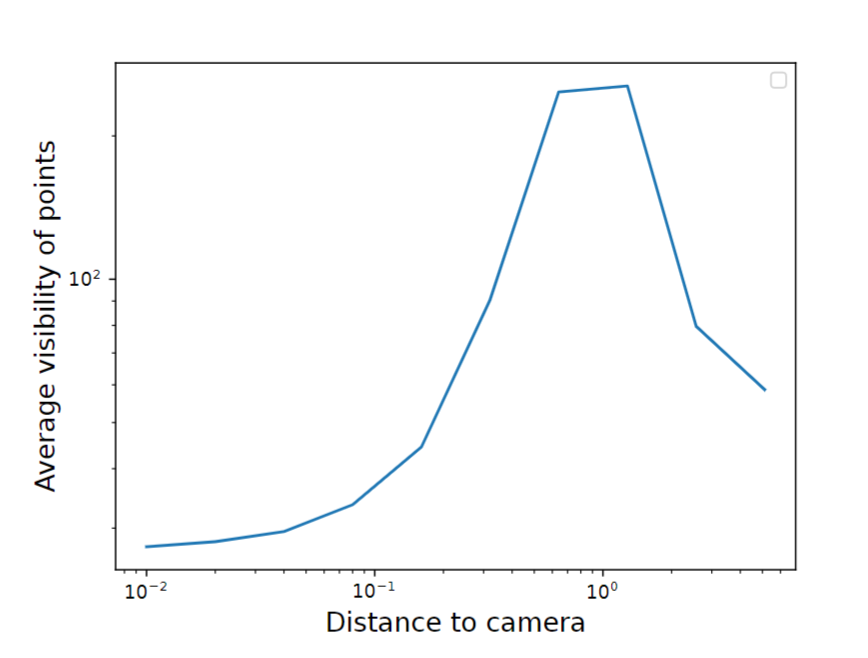
将看到光线上一个点的相机的平均数量可视化为到光线原点距离的函数。从各种方法[BMV∗22,CXG∗22,SSC22a,MESK22]对12个场景中所有摄像机的得分进行平均。大多数靠近摄像机的点只能被少数摄像机看到。能见度增加,直到达到被摄物的平均距离,然后再次下降
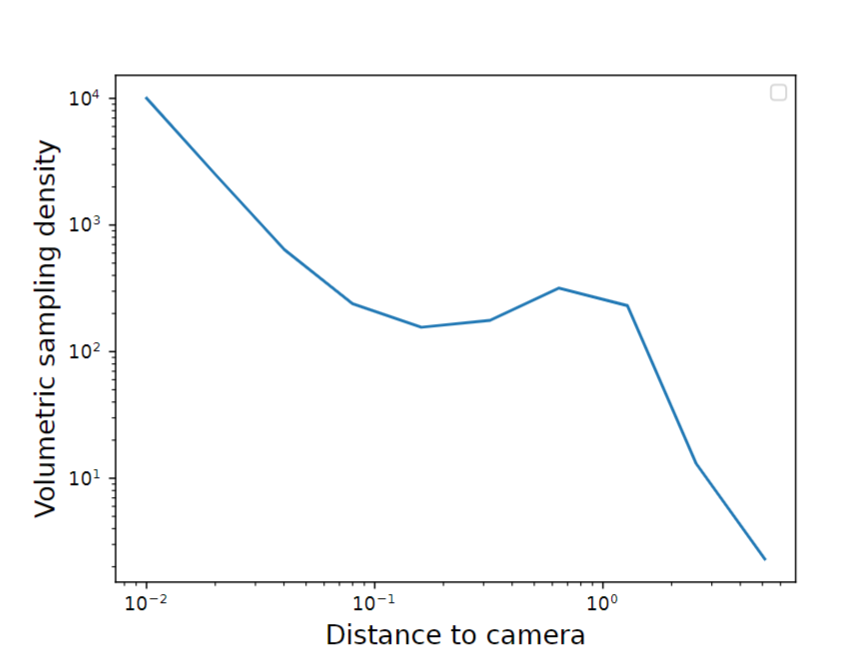
可视化的平均体积采样的光线在盆景场景作为一个函数到相机的距离。我们看到,尽管能见度很低,但靠近相机的体积单位仍被过度采样
Method
为了补偿靠近相机的采样密度不平衡,我们建议在反向传递期间缩放每个点特征(如密度或颜色)反向传播到NeRF表示(MLP,体素网格等)的梯度。我们建议采用以下梯度缩放:
$s_{\nabla p}=min(1,(\mathbf{\delta}_{p}^{i})^{2})$ Eq.4
也就是我们用$\nabla p\times s_{\nabla p}.$来代替$\nabla_{p}$。其中$\delta_{p}^{i}$是点到相机光线原点的距离。
这种缩放补偿了靠近相机的主要正方形密度,同时保持其余的梯度不变。请注意,给定点的缩放取决于光线投射的相机。
对于提出的方法,我们假设相机和捕获内容之间的典型距离为1个单位的距离。我们使用这个假设来推导Eq. 4,并且在我们的实验中没有调整场景比例,因为大多数场景都遵循这个假设。如果场景尺度与此假设有显著差异,并且捕获的内容处于σ单位距离的数量级,则权重可以替换为:$s_{\nabla P}=min(1,\frac{(\delta_{p}^{i})^{2}}{\sigma^{2}})$ Eq.5
在摄像机标定的基础上,有可能自动估计出σ。
直接作用于梯度是不常见的,但设计一个损失来达到类似的效果将是具有挑战性的: 损失需要访问样本的单个密度/颜色,因为不可能根据体积积分后的距离对单个点产生不同的影响。正则化单个密度/颜色会对它们的值施加先验,而缩放梯度会降低它们变化的速度。此外,密度为0的样品对前向颜色没有贡献,但可能会收到显著的梯度。添加新的损失意味着将该损失的梯度添加到其他损失/正则化器的梯度(微分求和规则),使其难以重现缩放的效果。
相比之下,梯度缩放是直接的,它改变了相机附近样本的密度/颜色的更新幅度,有助于避免局部最小值。
Non-linear space parameterization
一些方法[BMV * 22]使用坐标$f(p)\in\mathbb{R}^3\rightarrow\mathbb{R}^3$的非线性参数化将无界场景拟合到有界坐标中。在这种情况下,应该考虑空间的体积收缩来缩放梯度。这个收缩因子是雅可比矩阵$\mathbb{J}_{f}$ of f的行列式的绝对值。这样缩放就变成:
$s_{\nabla p}=min(1,\frac{(\delta_{p}^{i})^{2}}{|\det(\mathbb{J}_{f}(p)|})$
根据映射,$\det(\mathbb{J}_f(p))$计算起来可能不容易。在我们的实验中,我们没有使用它,但未来的工作可能需要它。事实上,在MipNeRF360中,场景的中心空间,包含大多数相机不受映射影响,因此雅可比矩阵是恒等式。
Implementation and performance
在PyTorch中使用自定义autograd实现此操作非常简单。函数,如图5中的10行代码所示。我们还在补充材料中提供了一个JAX实现,它直接与multinerf [MVS * 22]代码库兼容。使用此操作,可以在数据结构(MLP,哈希网格,体素等)采样之后,以及沿着射线的点积分之前插入对它的单个调用。这确保了每个点梯度是独立缩放的,同时影响控制其特征(密度和颜色)的权重。第4.2节中给出的代码在逆向传递300k个点时产生100μs的开销,这在~ 50ms迭代的上下文中可以忽略不计。它可以很容易地在大多数代码库中使用,只需进行最小的调整。

Evaluations
我们对广泛的体积重建方法和表示进行了经验评估。虽然我们没有对改进优化的收敛性提供理论分析,但我们发现所提出的缩放减少了所有测试方法的浮动数,同时保留或改进了包括优化损失在内的定量度量。
Clamped quadratic scaling
考虑到问题的性质,一个直接的候选方法可能是将梯度按$(\mathbf{\delta}_p^i)^2$缩放,以补偿采样密度的二次衰减。虽然这确实解决了近相机采样不平衡问题,但它会导致远离相机的非常强的梯度,从而无法正确学习如图6(中行)所示的曲面。
如式3所示,给定点的采样密度是所有摄像机采样密度之和的结果。这意味着在每个给定的相机附近,体积元素的采样密度的逆二次性质的假设大多是有效的,因为来自其他相机的采样在该区域可以忽略不计。因此,当到达场景的主要内容(深度为1左右)时,我们选择不修改梯度,让相机的分布引导这些区域的采样密度,如图4b所示。
让更多的相机看到一个点具有潜在的积极作用,因为它将样本集中在有趣的区域,而不是近相机采样不平衡,这纯粹是由于光线行进过程的性质而产生的伪影。我们在图6中说明,我们的梯度缩放方法有助于将梯度集中在场景中心附近,防止背景崩溃,并且使用纯二次缩放会导致更差的收敛和重建。
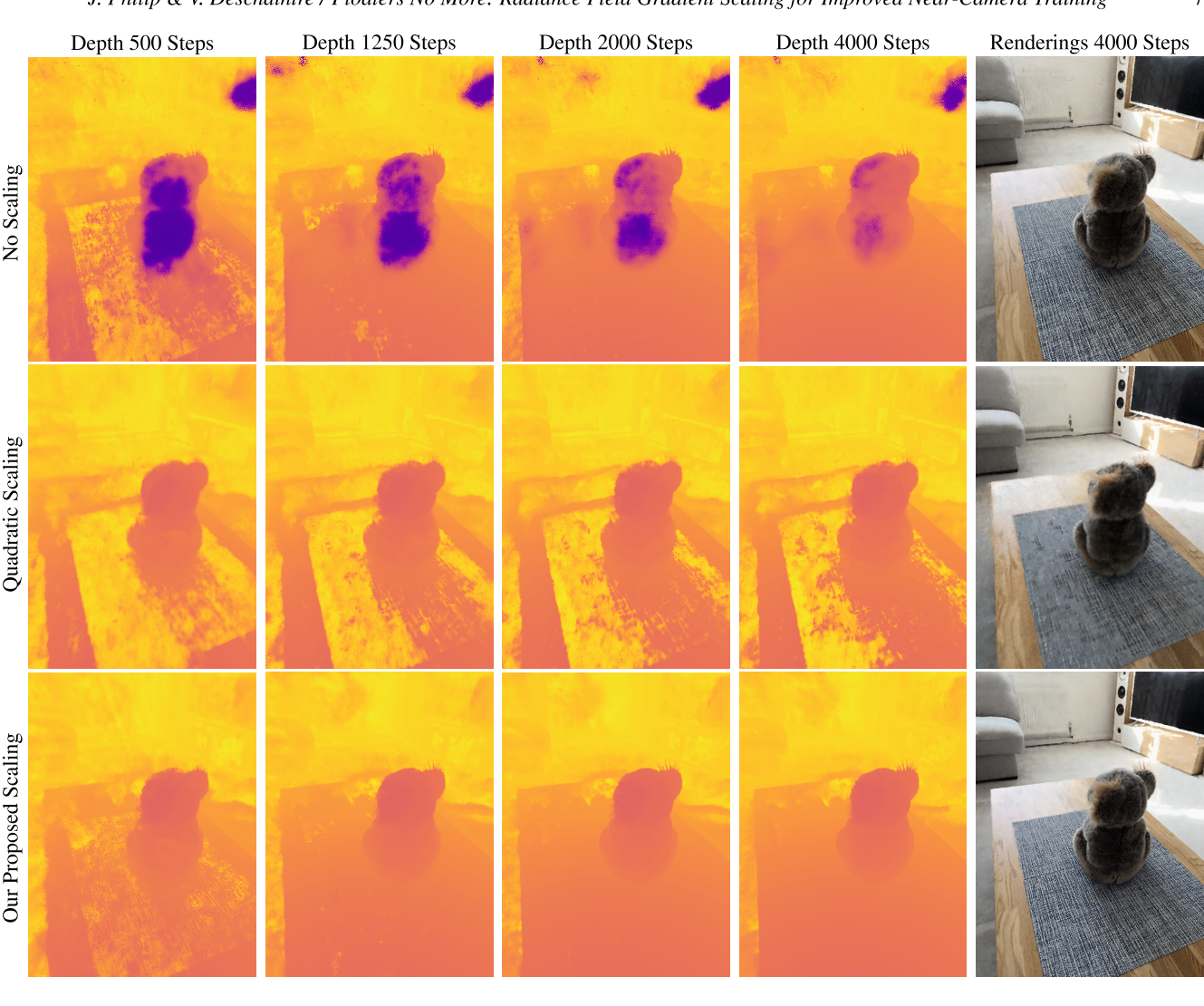
我们比较了使用NGP自定义实现的三种不同的梯度缩放方法[MESK22]。对于它们,我们设近平面为0。
- 在最上面一行中,我们可以看到,在没有任何缩放的情况下,密度在训练摄像机附近建立得非常快,虽然在优化过程中有些密度被删除了,但一些近距离摄像机密度最终保留了下来。
- 在中间一行,我们可以看到,纯二次缩放导致远密度的偏向。Table首先在背景重建,优化不会从这个错误的初始化中恢复。
- 我们在下面一行展示了我们的闭合梯度缩放的结果。我们清楚地看到了该方法的优点,该表的几何形状被快速而良好地重建,并且在没有背景崩溃的情况下收敛到更好的估计。
Gradient scaling for various NeRF representation
在本节中,我们将展示添加梯度缩放到各种现有方法的效果,并展示它删除了所有这些方法的背景折叠效果。这在补充材料中的视频中尤为明显。对于每种方法,我们都尽可能地使用它们的实现,导致不同颜色的深度编码,我们为每个图形定义它。除非另有说明,否则我们呈现测试视图。
- DVGO使用标量scalar体素网格表示密度,使用带有浅MLP的特征网格表示颜色
- Instant NGP使用多层哈希特征网格和浅MLP来表示场景的密度和颜色
- TensoRF使用表示场景的4D张量的因式分解来模拟密度和颜色
- MipNeRF360使用MLP和自定义频率编码在多个细节级别对场景进行建模,防止混叠,将MipNeRF360中的$\mathcal{L}_{dist}$与本文方法结合起来得到最好的效果
Quantitative evaluation and discussions
PSNR ↑ SSIM ↑ LPIPS ↓