Mip-NeRF

Title	Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields
Author	Jonathan T. Barron and Ben Mildenhall and Matthew Tancik and Peter Hedman and Ricardo Martin-Brualla and Pratul P. Srinivasan
Conf/Jour	2021 IEEE/CVF International Conference on Computer Vision (ICCV)
Year	2021
Project	google/mipnerf (github.com)
Paper	Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields (readpaper.com)

• 一种新的采样方式：锥体采样conical frustums截头圆锥体
• 基于PE提出了IPE，可以平滑地编码空间体积的大小和形状
• 将NeRF的粗精采样MLP合并为一个MLP

IPE：当锥体区域较宽（正态分布很宽）时，会将高频的信息积分为0；当区域较窄时，保持原来的PEncoding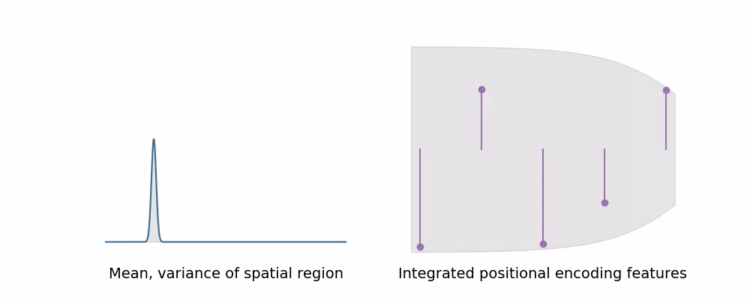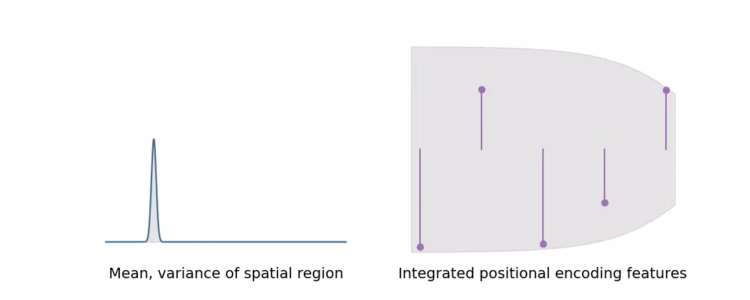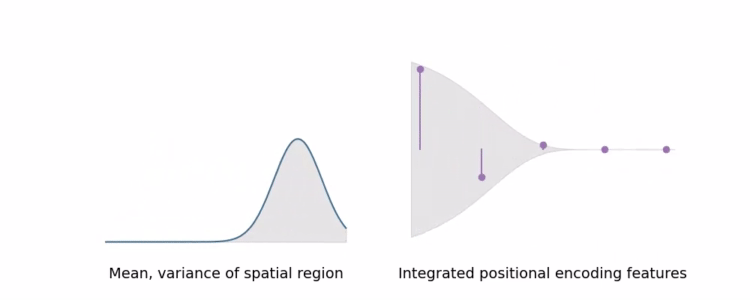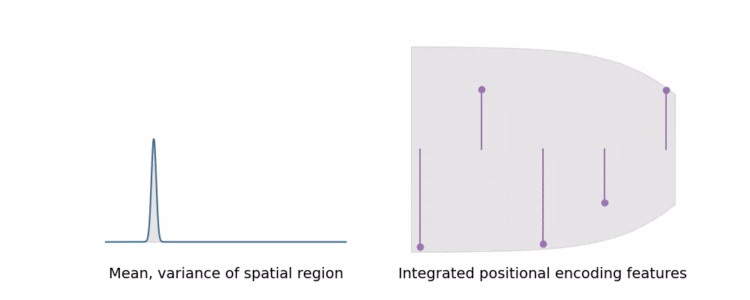

Conclusion

We have presented mip-NeRF, a multiscale NeRF-like model that addresses the inherent aliasingh混叠 of NeRF. NeRF works by casting rays, encoding the positions of points along those rays, and training separate neural networks at distinct scales.
In contrast, mip-NeRF casts cones, encodes the positions and sizes of conical frustums, and trains a single neural network that models the scene at multiple scales. By reasoning explicitly about sampling and scale, mip-NeRF is able to reduce error rates relative to NeRF by60% on our own multiscale dataset, and by 17% on NeRF’s single-scale dataset, while also being 7% faster than NeRF.Mip-NeRF is also able to match the accuracy of a bruteforce supersampled NeRF variant, while being 22× faster.
We hope that the general techniques presented here will be valuable to other researchers working to improve the performance of raytracing-based neural rendering models.

AIR

NeRF：使用一个像素对一条光线进行采样，当在不同分辨率下进行train和test渲染时，会产生excessively blurred or aliased

• 如果很直接地对每个像素采用多条光线，计算量将倍增

Mip-NeRF：tends NeRF to represent the scene at a continuously-valued scale

• By efficiently rendering anti-aliased conical frustums锥形截锥，减少了锯齿伪影
• 相比NeRF加速7%，且大小减半，mip-NeRF在NeRF数据集上降低了17%的平均错误率，在我们提出的数据集的具有挑战性的多尺度变体上降低了60%

Introduction

• Neural volumetric representations，eg:NeRF
• NeRF采样策略导致过度模糊和混叠excessive blurring and aliasing
• NeRF用连续的体积函数取代了传统的离散采样几何，参数化为多层感知器。为了渲染像素的颜色，NeRF通过该像素投射一条光线，并将其投射到其体积表示中，查询MLP中沿该光线采样的场景属性，并将这些值合成为单一颜色。
• NeRF渲染在较少人为的场景中表现出明显的伪影。当训练图像以多种分辨率观察场景内容时，从恢复的NeRF中获得的渲染在近距离视图中显得过于模糊，并且在远距离视图中包含混联伪影。一个直接的解决方案是采用离线光线追踪中使用的策略:通过在其足迹中行进多条光线对每个像素进行超采样。但是对于神经体积表示(如NeRF)来说，这是非常昂贵的，它需要数百个MLP评估来渲染单个光线，并且需要几个小时来重建单个场景。
• In this paper, we take inspiration from the mipmapping approach used to prevent aliasing in computer graphics rendering pipelines.
  • mipmap表示一组不同的离散下采样尺度的信号(通常是图像或纹理图)，并根据像素足迹到该射线相交的几何图形的投影选择适当的尺度用于射线。这种策略被称为预滤波，因为抗混叠的计算负担从渲染时间(如在蛮力超采样解决方案中)转移到预计算阶段-无论纹理渲染多少次，都只需要为给定纹理创建一次mipmap。
• Mip-NeRF: extends NeRF to simultaneously represent the prefiltered radiance field for a continuousspace of scales.
  • mip-NeRF的输入是一个三维高斯分布，它表示亮度场应该被积分的区域。如图1所示，然后，我们可以通过沿着一个圆锥的间隔查询mip-NeRF来呈现一个预过滤的像素，使用近似于像素对应的锥形截锥的高斯函数。为了对三维位置及其周围的高斯区域进行编码，我们提出了一种新的特征表示:集成位置编码(IPE)。这是NeRF的位置编码(PE)的一种推广，它允许空间的一个区域具有紧凑的特征，而不是空间中的单个点。
  • Mip-NeRF极大地提高了NeRF的准确性，并且在以不同分辨率观察场景内容的情况下(即相机移动到离场景更近或更远的设置)，这种好处甚至更大。在我们提出的具有挑战性的多分辨率基准上，mip-NeRF能够相对于NeRF平均降低60%的错误率(参见图2的可视化)。Mip-NeRF的尺度感知结构还允许我们将NeRF用于分层采样[30]的单独的“粗”和“细”MLP合并为单个MLP。因此，mip-NeRF比NeRF略快(约7%)，并且有一半的参数。

Related Work

我们的工作直接扩展了NeRF[30]，这是一种非常有影响力的技术，用于从观察到的图像中学习3D场景表示，以合成新颖的逼真视图。
我们回顾了计算机图形学和视图合成中使用的3D表示，包括最近引入的连续神经表示，如NeRF，重点是采样和混叠。

• Anti-aliasing in Rendering
  • 采样和混叠是计算机图形学中渲染算法发展过程中被广泛研究的基本问题。减少混叠(“抗混叠”)通常是通过超采样或预滤波来完成的。
  • 基于超采样的技术[46]在渲染时每像素投射多条光线，以便采样更接近奈奎斯特频率。这是一种减少混叠的有效策略，但代价很高，因为运行时间通常随超采样率线性扩展。因此，超采样通常只在脱机渲染上下文中使用。而不是采样更多的光线来匹配奈奎斯特频率，基于预滤波的技术使用场景内容的低通滤波版本来降低奈奎斯特频率所需的渲染场景没有混叠。
  • 预滤波技术[18,20,32,49]更适合实时渲染，因为场景内容的过滤版本可以提前预计算，并且可以在渲染时根据目标采样率使用正确的“比例”。在渲染环境中，预过滤可以被认为是通过每个像素跟踪一个锥而不是一条射线[1,16]:每当锥与场景内容相交时，在与锥的足迹对应的尺度上查询预先计算的场景内容的多尺度表示(例如稀疏体素八叉树[15,21]或mipmap[47])。
  • 我们的工作从图形工作中获得灵感，并为NeRF提供了多尺度场景表示。我们的策略在两个关键方面不同于传统图形管道中使用的多尺度表示。
    • 首先，我们无法预先计算多尺度表示，因为在我们的问题设置中，场景的几何形状是未知的——我们正在使用计算机视觉恢复场景的模型，而不是渲染预定义的CGI资产。因此，Mip-NeRF必须在训练期间学习场景的预过滤表示
    • 其次，我们的尺度概念是连续的，而不是离散的。mip-NeRF不是在固定数量的尺度上使用多个副本来表示场景(比如在mipmap中)，而是学习一个可以在任意尺度上查询的单一神经场景模型。
• Scene Representations for View Synthesis
  • 对于视图合成任务，已经提出了各种场景表示:使用观察到的场景图像来恢复表示，支持从未观察到的摄像机视点渲染场景的新颖逼真图像。当场景的图像被密集捕获时，可以使用光场插值技术[9,14,22]来渲染新的视图，而无需重建场景的中间表示。与采样和混叠相关的问题已在此设置中进行了深入研究[7]。
  • 从稀疏捕获的图像合成新视图的方法通常重建场景的3D几何形状和外观的明确表示。许多经典的视图合成算法使用基于网格的表示以及漫射[28]或视图相关[6,10,48]纹理。
    • Mesh-based：基于网格的表示可以有效地存储，并且自然地与现有的图形渲染管道兼容。然而，由于不连续性和局部最小值，使用基于梯度的方法来优化网格几何和拓扑通常是困难的。因此，体积表示在视图合成中变得越来越流行。
    • 早期的方法直接使用观察到的图像对体素网格着色[37]，而最近的体积方法使用基于梯度的学习来训练深度网络来预测场景的体素网格表示[12,25,29,38,41,53]。基于离散体素的表示对于视图合成是有效的，但它们不能很好地扩展到更高分辨率的场景
    • coordinate-based：计算机视觉和图形学研究的最新趋势是用基于坐标的神经表示取代这些离散表示，将3D场景表示为由mlp参数化的连续函数，这些函数从3D坐标映射到该位置的场景属性。一些最近的方法使用基于坐标的神经表征将场景建模为隐式曲面[31,50]，但最近的大多数视图合成方法都是基于体积NeRF表征[30]。NeRF启发了许多后续作品，将其连续神经体表示扩展到生成建模[8,36]，动态场景[23,33]，非刚性变形物体[13,34]，具有变化照明和遮挡物的摄影旅游设置[26,43]，以及用于重照明的反射建模[2,3,40]
    • 在使用基于坐标的神经表示的视图合成上下文中，对采样和混叠问题的关注相对较少。用于视图合成的离散表示，如多边形网格和体素网格，可以使用传统的多尺度预滤波方法(如mipmaps和八叉树)有效地渲染而不存在混叠。然而，基于坐标的视图合成的神经表示目前只能使用超采样来抗锯齿，这加剧了它们已经缓慢的渲染过程。Takikawa等人最近的工作[42]提出了一种基于稀疏体素八叉树的多尺度表示，用于隐式表面的连续神经表示，但他们的方法要求场景几何是先验的，而不是我们的视图合成设置，其中唯一的输入是观察到的图像。
    • Mip-NeRF解决了这个开放的问题，在训练和测试期间实现了抗混叠图像的高效渲染，以及在训练期间使用多尺度图像。

Preliminaries: NeRF

NeRF采样：射线r(t) = o + td从相机的投影o的中心沿方向发射，使其穿过像素。用于确定相机预定义的近平面和远平面tn和tf之间排序距离t的向量。对于每个距离tk∈t，我们计算它在射线x = r(tk)上对应的3D位置，然后使用位置编码对每个位置进行编码，编码后输入进MLP得到密度和颜色

• NeRF的保真度主要取决于位置编码的使用，因为它允许将场景参数化的MLP表现为插值函数，其中L决定插值内核的带宽

训练NeRF很简单:使用一组已知相机姿势的观察图像，我们使用梯度下降最小化所有输入像素值和所有预测像素值之间的平方差之和。
构建了两个MLP，一粗一精，两者结合进行预测color和density
$\begin{aligned}\min_{\Theta^c,\Theta^f}\sum_{\mathbf{r}\in\mathcal{R}}\left(\left|\mathbf{C}^(\mathbf{r})-\mathbf{C}(\mathbf{r};\Theta^c,\mathbf{t}^c)\right|_2^2\+\left|\mathbf{C}^(\mathbf{r})-\mathbf{C}(\mathbf{r};\Theta^f,\text{sort}(\mathbf{t}^c\cup\mathbf{t}^f))\right|_2^2\right)\end{aligned}$

• 粗采样：均匀采样64个点$t^f$
• 精采样：经过粗MLP——权重参数$\Theta^c$计算得到的密度，然后计算出权重，使用逆变换采样得到128个精采样点
• 最后使用总共192个采样点，使用精MLP得出密度和颜色

Method

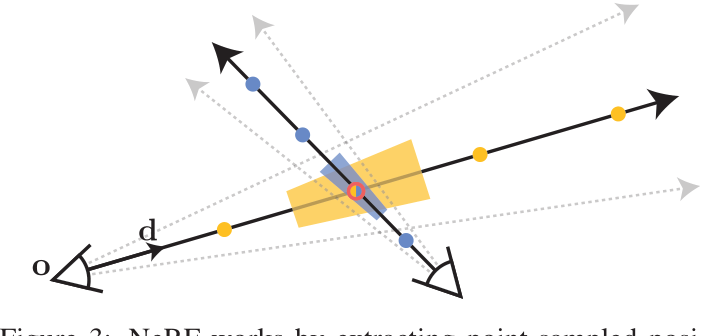
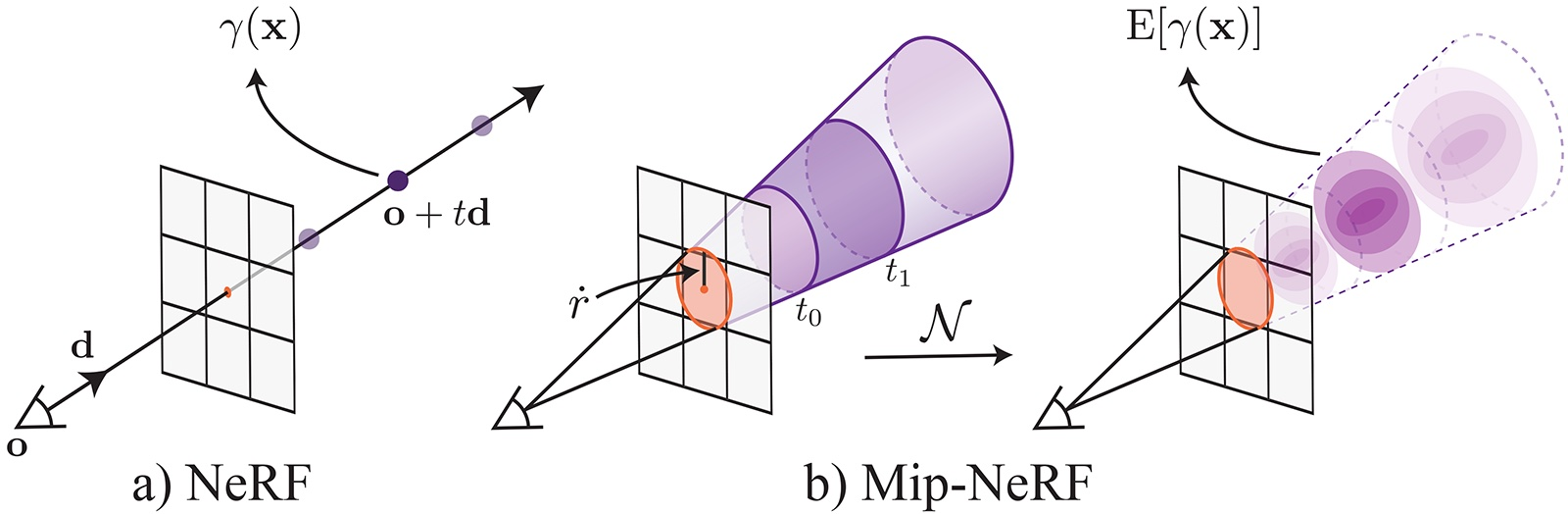
NeRF的工作原理是沿着每个像素的射线提取点采样的位置编码特征(这里显示为点)。这些点采样特征忽略了每条射线所观察到的体积的形状和大小，因此两台不同的相机在不同尺度下对同一位置成像可能会产生相同的模糊点采样特征，从而显著降低了NeRF的性能。相比之下，Mip-NeRF投射锥而不是射线，并明确地对每个采样的锥形截体(在这里显示为梯形)的体积进行建模，从而解决了这种模糊性。

MipNeRF通过从每个像素投射一个锥体来改善这个问题。我们不是沿着每条射线进行点采样，而是将被投射的锥体划分为一系列锥形截锥(垂直于其轴线切割的锥体)。我们不是从空间中的无限小点构造位置编码(PE)特征，而是构造一个由每个圆锥截体所覆盖的体积的集成位置编码(IPE)表示。这些变化使MLP能够推断出每个锥形截锥体的大小和形状，而不仅仅是它的质心。锥形锥台和IPE特征的使用也使我们能够将NeRF的两个独立的“粗”和“细”MLP减少到一个单一的多尺度MLP，从而提高了训练和评估速度，并将模型大小减少了50%。

Cone Tracing and Positional Encoding

mipNeRF中的图像一次渲染一个像素，对于该像素，我们从相机的投影中心o沿穿过像素中心的方向d投射一个锥体

• 圆锥顶点为o，在像平面上半径$\dot r$，以$\frac{2}{\sqrt{12}}$缩放世界坐标系下的像素宽度得到。

位于两个t值[t0, t1]之间的锥形截锥内位置x的集合：

$$\begin{aligned}\mathrm{F}(\mathbf{x},\mathbf{o},\mathbf{d},\dot{r},t_0,t_1)&=\mathbb{1}\bigg\{\bigg(t_0<\frac{\mathbf{d}^\mathrm{T}(\mathbf{x}-\mathbf{o})}{\left\|\mathbf{d}\right\|_2^2}<t_1\bigg) \\\land\bigg(\frac{\mathbf{d}^\mathrm{T}(\mathbf{x}-\mathbf{o})}{\left\|\mathbf{d}\right\|_2\left\|\mathbf{x}-\mathbf{o}\right\|_2}>\frac{1}{\sqrt{1+(\dot{r}/\left\|\mathbf{d}\right\|_2)^2}}\bigg)\bigg\},\end{aligned}$$

• $\mathbb{1}(\cdot)$指标函数，iff x在$(\mathbf{o},\mathbf{d},\dot{r},t_0,t_1)$定义的圆锥内F(x, ·) = 1
• 与 $\land$ ， 或$\vee$

我们现在必须构造一个圆锥形截体内体积的特征表示。理想情况下，这种特征表示应该与NeRF中使用的位置编码特征具有相似的形式，正如Mildenhall等人所表明的，这种特征表示对NeRF的成功至关重要[30]。对此有许多可行的方法(参见附录以进一步讨论)，但我们发现的最简单和最有效的解决方案是简单地计算圆锥锥内所有坐标的预期位置编码:

$\gamma^*(\mathbf{o},\mathbf{d},\dot{r},t_0,t_1)=\frac{\int\gamma(\mathbf{x})\mathrm{F}(\mathbf{x},\mathbf{o},\mathbf{d},\dot{r},t_0,t_1)d\mathbf{x}}{\int\mathrm{F}(\mathbf{x},\mathbf{o},\mathbf{d},\dot{r},t_0,t_1)d\mathbf{x}}.$

然而，目前尚不清楚如何有效地计算这样的特征，因为分子中的积分没有封闭形式的解。因此，我们用多元高斯函数近似锥形截锥体，这允许对所需特征进行有效逼近，我们将其称为“集成位置编码”(IPE)。

为了用多元高斯函数近似圆锥体，我们必须计算平均值和协方差of F(x，·)。因为假设每个圆锥截体都是圆形的，并且因为圆锥截体围绕锥轴是对称的，这样的高斯分布完全由三个值(除了o和d之外)表征:沿射线的平均距离$μ_t$，沿射线$σ^{2}_{t}$的方差，垂直于射线$σ^{2}_{r}$的方差:

$\begin{aligned}\mu_t&=t_\mu+\frac{2t_\mu t_\delta^2}{3t_\mu^2+t_\delta^2},\quad\sigma_t^2=\frac{t_\delta^2}{3}-\frac{4t_\delta^4(12t_\mu^2-t_\delta^2)}{15(3t_\mu^2+t_\delta^2)^2},\\\sigma_r^2&=\dot{r}^2\bigg(\frac{t_\mu^2}{4}+\frac{5t_\delta^2}{12}-\frac{4t_\delta^4}{15(3t_\mu^2+t_\delta^2)}\bigg).\end{aligned}$

其中$t_{\mu} = \frac{t_{0} + t_{1}}{2}$,$t_{\delta} = \frac{t_{1}-t_{0}}{2}$

我们可以将这个高斯函数从锥形截锥体的坐标系转换为如下的世界坐标:

$\mu=\mathbf{o}+\mu_t\mathbf{d},\quad\Sigma=\sigma_t^2\big(\mathbf{d}\mathbf{d}^\mathrm{T}\big)+\sigma_r^2\bigg(\mathbf{I}-\frac{\mathbf{d}\mathbf{d}^\mathrm{T}}{\left|\mathbf{d}\right|_2^2}\bigg)$,得到最终的多元高斯函数。

接下来，我们推导出IPE，它是根据前面提到的高斯分布的位置编码坐标的期望。为了实现这一点，首先将公式1中的PE重写为傅里叶特征[35,44]是有帮助的:

$\gamma(\mathbf{x})=\Big[\sin(\mathbf{x}),\cos(\mathbf{x}),\ldots,\sin\bigl(2^{L-1}\mathbf{x}\bigr),\cos\bigl(2^{L-1}\mathbf{x}\bigr)\Big]^{\mathrm{T}.}$

$\mathbf{P}=\begin{bmatrix}1&0&0&2&0&0& \cdots &2^{L-1}&0&0\\0&1&0&0&2&0&\cdots&0&2^{L-1}&0\\0&0&1&0&0&2& \cdots &0&0&2^{L-1}\end{bmatrix},\gamma(\mathbf{x})=\begin{bmatrix}\sin(\mathbf{Px})\\\cos(\mathbf{Px})\end{bmatrix}.$

$\mathrm{(Cov[Ax,By]~=~A~Cov[x,y]B^T)}$

均值和协方差：$\mu_{\gamma}=\mathrm{P}\mu,\quad\Sigma_{\gamma}=\mathrm{P}\Sigma\mathrm{P}^{\mathrm{T}}.$

产生IPE特征的最后一步是计算这个提升的多元高斯的期望，由位置的正弦和余弦调制。这些期望有简单的封闭形式表达式:

$\begin{aligned}\operatorname{E}_{x\sim\mathcal{N}(\mu,\sigma^2)}[\sin(x)]&=\sin(\mu)\exp\Big(-(^1/2)\sigma^2\Big),\\\operatorname{E}_{x\sim\mathcal{N}(\mu,\sigma^2)}[\cos(x)]&=\cos(\mu)\exp\Big(-(^1/2)\sigma^2\Big).\end{aligned}$

我们看到这个期望的正弦或余弦仅仅是均值的正弦或余弦被方差的高斯函数衰减。有了这个，我们可以计算我们的最终IPE特征as 期望的正弦和余弦的平均值和协方差矩阵的对角线:

$$\begin{aligned} \gamma(\mathbf{\mu},\mathbf{\Sigma})& =\mathrm{E}_{\mathbf{x}\sim\mathcal{N}(\mathbf{\mu}_\gamma,\mathbf{\Sigma}_\gamma)}[\gamma(\mathbf{x})] \\ &=\begin{bmatrix}\sin(\mathbf{\mu}_\gamma)\circ\exp(-(1/2)\mathrm{diag}(\mathbf{\Sigma}_\gamma))\\\cos(\mathbf{\mu}_\gamma)\circ\exp(-(1/2)\mathrm{diag}(\mathbf{\Sigma}_\gamma))\end{bmatrix} \end{aligned}$$

$\circ$表示逐元素的乘法。因为位置编码独立地编码每个维度，这种预期的编码只依赖于$\gamma(x)$的边际分布，并且只需要协方差矩阵的对角线(每个维度方差的向量)。Because$\sum_{\gamma}$由于其相对较大的尺寸，计算成本过高，我们直接计算$\sum_{\gamma}$的对角线:$\operatorname{diag}(\mathbf{\Sigma}_{\gamma})=\Big[\operatorname{diag}(\mathbf{\Sigma}),4\operatorname{diag}(\mathbf{\Sigma}),\ldots,4^{L-1}\operatorname{diag}(\mathbf{\Sigma})\Big]^\mathrm{T}$

这个向量只依赖于3D位置的协方差Σ的对角线，可以计算为:

$\operatorname{diag}(\mathbf{\Sigma})=\sigma_t^2(\mathbf{d}\circ\mathbf{d})+\sigma_r^2\left(\mathbf{1}-\frac{\mathbf{d}\circ\mathbf{d}}{\left|\mathbf{d}\right|_2^2}\right).$

如果直接计算这些对角线，那么构建IPE特征的成本与构建PE特征的成本大致相同。

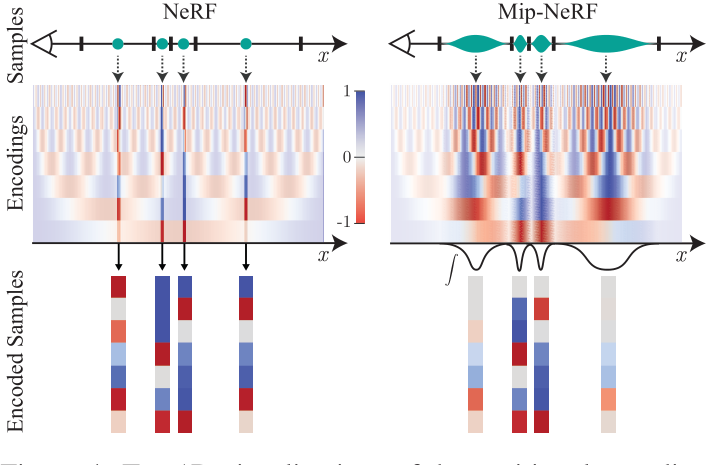
In a toy 1D domain : IPE 和传统 PE 特征之间的差异
IPE 特征的行为直观：如果位置编码中的特定频率有一个大于用于构建 IPE 特征的区间宽度的周期，则该频率处的编码不受影响。但是如果周期小于区间（在这种情况下，该区间上的 PE 将重复振荡），那么该频率处的编码会缩小到零。（sin、cos: 许多交叉的-1和1导致积分后编码变为0，如图）
简而言之，IPE 保留了在区间上恒定的频率，并软“删除”频率在区间上变化，而 PE 保留了直到某个手动调整的超参数 L 的所有频率。
通过以这种方式缩放每个正弦和余弦，IPE 特征实际上是抗锯齿位置编码特征，可以平滑地编码空间体积的大小和形状。IPE 还有效地将 L 从超参数中删除：它可以简单地设置为非常大的值，然后永远不会调整

Architecture

除了锥跟踪和IPE特征外，mip-NeRF的行为类似于NeRF，如第2.1节所述。
对于渲染的每个像素，而不是像NeRF中那样的光线，投射一个锥体。我们没有沿射线采样$t_{k}$的n个值，而是采样$t_{k}$的n + 1个值，计算跨越每对相邻采样$t_{k}$值的区间的IPE特征，如前所述，这些IPE特征作为输入传递到MLP中，以产生密度和颜色，如公式2所示。mip-NeRF中的渲染遵循公式3。

$\forall t_k\in\mathbf{t},\quad[\tau_k,\mathbf{c}_k]=\mathrm{MLP}(\gamma(\mathbf{r}(t_k));\Theta).$

$\begin{aligned}\mathbf{C}(\mathbf{r};\Theta,\mathbf{t})&=\sum_kT_k(1-\exp(-\tau_k(t_{k+1}-t_k)))\mathbf{c}_k,\\\text{with}\quad T_k&=\exp\left(-\sum_{k’<k}\tau_{k’}(t_{k’+1}-t_{k’})\right),\end{aligned}$

我们的圆锥变换和 IPE 特征允许我们明确地将尺度编码到我们的输入特征中，从而使 MLP 能够学习场景的多尺度表示。因此，Mip-nerF 使用具有参数 Θ 的单个 MLP，我们在分层采样策略中反复查询。这有多个好处：模型大小被切割一半，渲染更准确，采样效率更高，整体算法更简单。我们的优化问题是：(loss)

$$\min_{\Theta}\sum_{\mathbf{r}\in\mathcal{R}}(\lambda\left\|\mathbf{C}^{*}(\mathbf{r})-\mathbf{C}(\mathbf{r};\Theta,\mathbf{t}^{c})\right\|_{2}^{2}+\left\|\mathbf{C}^{*}(\mathbf{r})-\mathbf{C}(\mathbf{r};\Theta,\mathbf{t}^{f})\right\|_{2}^{2})$$

通过超参数$\lambda = 0.1$实现粗loss与精loss的平衡

采样点：

• NeRF：C64+F64+128
• Mip-NeRF：C128+F128

权重：
$w_k’=\frac{1}{2}(\max(w_{k-1},w_k)+\max(w_k,w_{k+1}))+\alpha.$

• We filter w with a 2-tap max filter followed by a 2-tap blur filter (a “blurpool” [51]), which produces a wide and smooth upper envelope上包络 on w
• A hyperparameter α is added to that envelope before it is re-normalized to sum to 1, which ensures that some samples are drawn even in empty regions of space (we set α = 0.01 in all experiments). 确保了空区域也会抽取一些样本

Mip-NeRF 在 JaxNeRF [11] 之上实现，JaxNeRF 是一种 JAX [4] 重新实现的 NeRF，它实现了比原始 TensorFlow 实现更高的精度并训练速度更快。
细节：

• 1 million iterations of Adam [19] with a batch size of 4096
• a learning rate that is annealed logarithmically from $5 · 10^{−4}$ to $5 · 10^{−6}$

有关其他细节的补充以及 JaxNeRF 和 mip-NeRF 之间的一些额外差异，这些差异不会显着影响性能，并且是我们的主要贡献附带的：锥体追踪、IPE 和使用单个多尺度 MLP。

Result

NeRF-blender dataset上评估PSNR、SSIM、LPIPS以及：
To enable easier comparison , we also present an “average” error metric that summarizes all three metrics: the geometric mean of $MSE = 10^{−PSNR/10}$, $\sqrt{1 − SSIM}$ (as per [5]), and LPIPS.

我们还报告了运行时(wall time的中位数和中值绝对偏差)，以及NeRF和mip-NeRF的每个变体的网络参数数量。所有 JaxNeRF 和 mip-NeRF 实验都在具有 32 个内核的 TPU v2 上进行训练

NeRF原始Blender数据集缺陷：所有相机的焦距和分辨率相同，且放在与对象相同的距离上
Mip-NeRF构建了自己的多尺度Blender benchmark：相机距离物体不同，可能放大或缩小