QiYun

Note

NeUDF

Posted on Edited on In
4.1k 15 mins.
Title NeUDF: Leaning Neural Unsigned Distance Fields with Volume Rendering
Author Yu-Tao Liu1,2 Li Wang1,2 Jie Yang1,2 Weikai Chen3 Xiaoxu Meng3 Bo Yang3 Lin Gao1,2*
Conf/Jour CVPR
Year 2023
Project NeUDF (CVPR 2023) (geometrylearning.com)
Paper NeUDF: Leaning Neural Unsigned Distance Fields with Volume Rendering (readpaper.com)

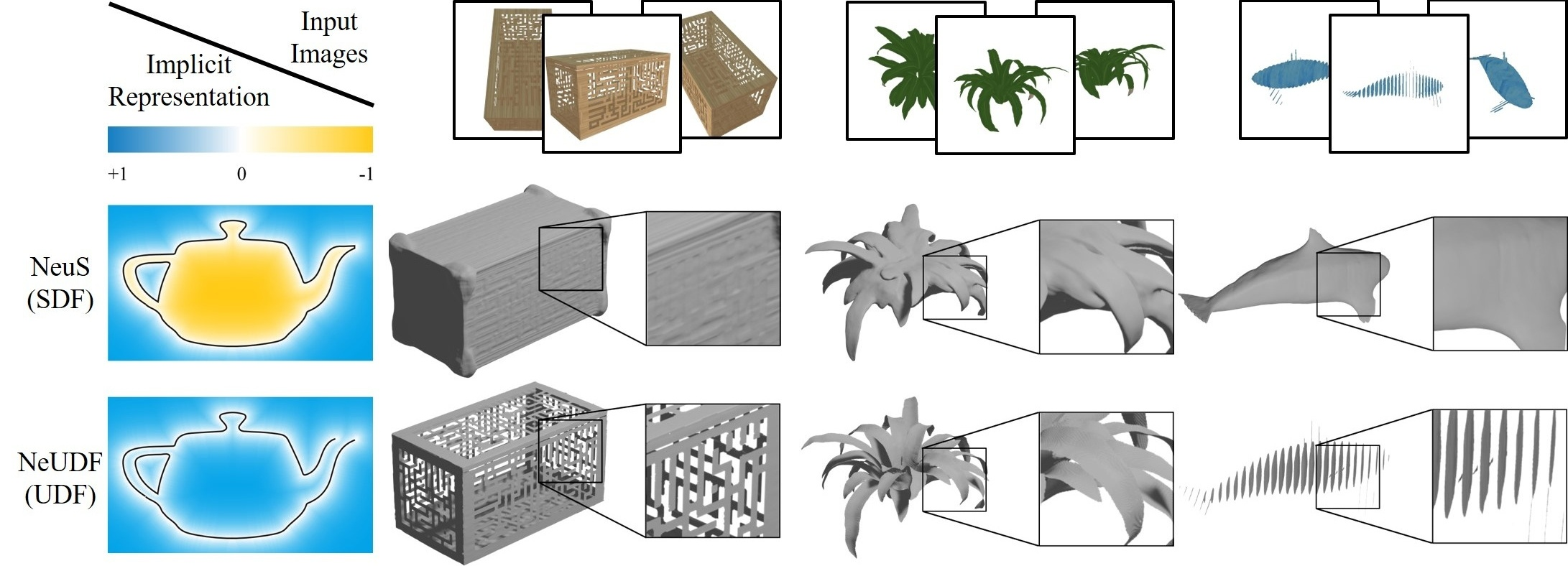
image.png

解决了Neus中SDF的一个限制：仅限于封闭表面的重建，无法重建包含开放表面结构的广泛的现实世界对象
NeUDF使用UDF：仅从多视图监督中重建具有任意拓扑的表面

  • 提出了两个专门为基于UDF的体渲染量身定制的权重函数的新公式
    • $w_r(t)=\tau_r(t)e^{-\int_0^t\tau_r(u)du}$ Eq.4
    • $\tau_r(t)=\left|\frac{\frac{\partial(\varsigma_r\circ\Psi\circ p)}{\partial t}(t)}{\varsigma_r\circ\Psi\circ p(t)}\right|$ Eq.5
      • $\varsigma_{r}(d) = \frac x{1+x}$
      • UDF: $d=\Psi_{\mathcal{O}}(x)$
  • 为了应对开放表面渲染，当输入/输出测试不再有效时，我们提出了一种专用的法向正则化策略来解决表面方向模糊问题
    • 用邻近的插值法向替换原始采样的表面法向

局限：

  • 无法重建透明表面
  • 平滑度和高频细节无法同时拥有
  • 需要额外的网格划分工具，导致重构误差
  • 展望：透明表面、稀疏视图

Discussions&Conclusions

局限性

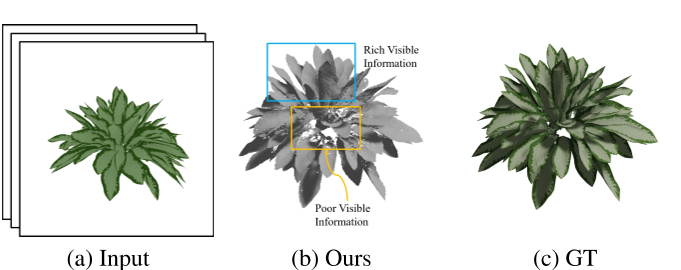
  • 首先，很难用我们的公式来模拟透明表面。当输入图像中没有足够的可见信息(例如视点稀疏或严重遮挡)时，重建质量会下降，图11给出了一个失败案例的例子。
  • 由于正态正则化会累积附近信息以减轻表面法向模糊，因此在平滑度和高频细节之间也存在权衡。
  • 此外，由于我们引入UDF是为了更好的表示能力，我们需要额外的网格划分工具，如MeshUDF[19]或SPSR[23]，这可能会引入更多的重构误差。

image.png

我们提出了NeUDF，这是一种新的基于UDF的体绘制方法，用于从有或没有掩码的2D图像中实现任意形状的高保真多视图重建。NeUDF 在定性和定量上都优于最先进的方法，尤其是在具有开放边界的复杂表面上。因此，我们的 NeUDF 可以在真实世界的 3D 应用程序中发挥关键作用。
在未来的工作中，我们可以扩展我们的公式以更好地重建透明表面。增强我们的 NeUDF 以支持稀疏输入图像也是一个有趣的未来方向。

AIR

由于神经隐式表面绘制的最新进展，多视图形状重建取得了令人印象深刻的进展。然而，现有的基于符号距离函数(SDF)的方法仅限于封闭表面，无法重建包含开放表面结构的广泛的现实世界对象。在这项工作中，我们引入了一个新的神经渲染框架，编码为NeUDF，它可以仅从多视图监督中重建具有任意拓扑的表面。为了获得表示任意曲面的灵活性，NeUDF利用无符号距离函数(unsigned distance function, UDF)作为曲面表示。虽然基于sdf的神经渲染器的简单扩展不能扩展到UDF，但我们提出了两个专门为基于UDF的体渲染量身定制的权重函数的新公式。此外，为了应对开放表面渲染，当输入/输出测试不再有效时，我们提出了一种专用的正态正则化策略来解决表面方向模糊问题。我们在许多具有挑战性的数据集上广泛评估了我们的方法，包括DTU [21]， MGN[5]和Deep Fashion 3D[61]。实验结果表明，在多视图曲面重建任务中，特别是对于具有开放边界的复杂形状，NeUDF可以显著优于最先进的方法。

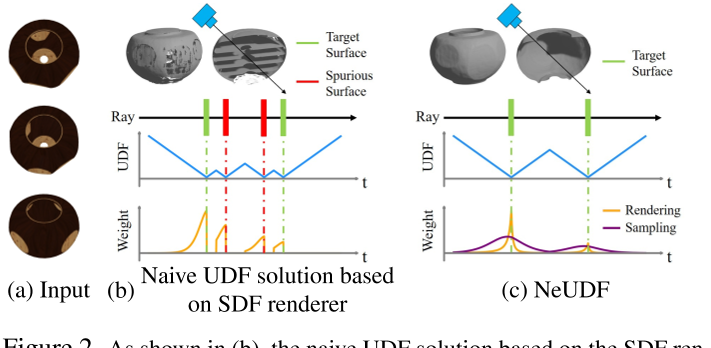
NeUDF建立在无符号距离函数(unsigned distance function, UDF)的基础上，UDF是一个简单的隐式函数，它返回从查询点到目标曲面的绝对距离。尽管它很简单，但我们表明，将基于sdf的神经渲染机制天真地扩展到无符号距离场并不能确保非水密表面的无偏渲染。特别是，如图2所示，基于sdf的加权函数会生成虚假曲面，其中渲染权重会在空洞区域触发不希望的局部最大值。为了解决这个问题，我们提出了一个新的无偏加权范式，专门为UDF量身定制，同时意识到表面遮挡。为了适应所提出的加权函数，我们进一步提出了一种定制的重要性采样策略，以确保非水密表面的高质量重建。此外，为了解决零等值面附近udf梯度不一致的问题，我们引入了一种正态正则化方法，利用曲面邻域的正态信息来增强梯度一致性。

image.png

我们的贡献总结如下:

  • 第一个基于udf的神经体绘制框架，称为NeUDF，可用于具有任意拓扑的形状的多视图重建，包括具有开放边界的复杂形状。
  • 针对UDF渲染提出了一种新的无偏加权函数和重要采样策略。
  • 在具有非水密3D形状(带有孔洞)的许多具有挑战性的数据集上进行多视图表面重建的最新性能

RW

  • Neural Implicit Representation
  • Neural Rendering
  • Multi-view Reconstruction
    • SDF+NR = Neus

Methodology

给定一组物体或场景的校准图像$\{\mathcal{I}_k|1\leq k\leq n\}$，我们的目标是仅使用二维图像监督来重建任意表面，包括封闭和开放结构。在本文中，曲面被表示为无符号距离函数(udf)的零水平集。为了学习对象或场景的UDF表示，我们引入了一种新的神经渲染架构，该架构包含用于渲染的无偏权重公式。

  • 首先定义基于UDF的场景表示(第3.1节)。
  • 然后，我们介绍了NeUDF，并为基于udf的体绘制专门定制了两个关键的权重函数公式(第3.2节)
  • 最后，我们说明了用于减轻2D图像歧义的正常正则化(第3.3节)和我们的loss配置(第3.4节)。

Scene Representation

与有符号距离函数(SDF)不同，无符号距离函数(UDF)是无符号的，能够表示任意拓扑的开放表面，除了水密表面。
给定一个三维物体$\mathcal{O}=\{V,F\}$，其中V和F是顶点和面的集合，物体$\mathcal{O}$的UDF可以表示为一个函数$d=\Psi_{\mathcal{O}}(x):\mathbb{R}^3\mapsto\mathbb{R}^+,$，它将一个点坐标映射到表面的欧几里得距离d。我们定义$\mathrm{UDF}_{\mathcal{O}}=\{\Psi_{\mathcal{O}}(x)|d<\epsilon,d=\mathrm{argmin}_{f\in F}(|x-f|_2)\},$，其中ε是一个小阈值，目标表面可以被UDFO的零水平集调制。
我们引入了一个可微体绘制框架来从输入图像中预测UDF。该框架由神经网络ψ近似，该网络根据沿采样射线v的空间位置x预测UDF值d和渲染颜色c:
$(d,c)=\psi(v,x):\mathbb{S}^2\times\mathbb{R}^3\mapsto(\mathbb{R}^+,[0,1]^3)$ Eq.1

在体绘制的帮助下，权重通过最小化预测图像$\mathcal{I}_{k}^{\prime}$和真实图像$\mathcal{I}_{k}$之间的距离来优化
学习到的表面$\mathcal{S}_{\mathcal{O}}$可以用预测UDF的零水平集表示:$\mathcal{S}_{\mathcal{O}}=\{x\in\mathbb{R}^{3}|d=0,(d,c)=\psi(v,x)\}$ Eq.2

NeUDF Rendering

渲染过程是学习准确UDF的关键，因为它通过沿射线v的积分将输出颜色和UDF值连接起来
$C(o,v)=\int_{0}^{+\infty}w(t)c(p(t),v)dt,$ Eq.3

其中C(o, v)为从相机原点0开始沿视点方向v的输出像素颜色，w(t)为点p(t)的权值函数，C(p(t)， v)为点p(t)沿视点方向v的颜色。
为了通过体绘制重建UDF，我们首先引入一个概率密度函数$\varsigma_r^{\prime}(\Psi(x)),$，称为U-density，其中Ψ(x)是x的无符号距离。密度函数$\varsigma_r^{\prime}(\Psi(x))$将UDF场映射到概率密度分布，该分布在表面附近具有显著的高值，以便准确重建。受Neus[53]的启发，我们推导了一个无偏和闭塞的权函数$w_{r}(t)$及其不透明密度$\tau_r(t)$

  • $w_r(t)=\tau_r(t)e^{-\int_0^t\tau_r(u)du}$ Eq.4
  • $\tau_r(t)=\left|\frac{\frac{\partial(\varsigma_r\circ\Psi\circ p)}{\partial t}(t)}{\varsigma_r\circ\Psi\circ p(t)}\right|$ Eq.5

其中◦是函数组合操作符，并且为了有效的UDF重建，必须满足以下规则:

  • $\varsigma_r(0)=0,\lim_{d\to+\infty}\varsigma_r(d)=1$ Eq.6
    • 在d=0，即表面处，权重大，概率密度函数值为1
  • $\varsigma_r’(d)>0;\varsigma_r’’(d)<0,\forall d>0$ Eq.7

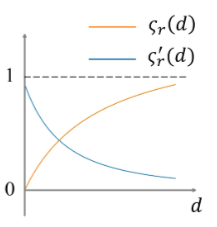
image.png
变量$\varsigma_r(d)$可以是图所示的任意函数。由于$\varsigma_{r}(d)$是u密度的累积分布函数，所以$\varsigma_r(0)=0$保证了负距离的点没有累积密度。此外，$\varsigma_r^{\prime}(d)>0$和$\varsigma_{r}^{\prime\prime}(d)<0$确保靠近表面的点的u密度值为正且显著高。$\varsigma_r(d)$中参数r是可学习的，控制着密度的分布。该函数结构解决了体绘制和表面重建之间的体面差距，保证了整体无偏性。详细讨论请参考我们的补充 我们认为，基于sdf的神经渲染器的幼稚扩展将违反上述一些规则。例如，**Neus**[53]中**u密度的累积分布函数**为$Φ_s$(Sigmoid function)， $Φ_s(0) > 0$违反式6。这种违背会导致权重渲染的偏差，从而导致多余的浮面和不规则的噪声，如图2所示。注意，Neus中提出的局部最大约束不能解决UDF中的这种呈现偏差。请查看我们补充资料中关于无偏性和全局/局部极大约束的详细讨论。和全局/局部最大约束的详细讨论。

在广泛评估了消融研究中不同形式的$\varsigma_{r}(d)$后(第4.3节)，我们最终选择$\varsigma_{r}(d) = \frac{rd}{1+rd}$, r初始化为0.05。进一步，我们采用α-合成对权函数进行离散化，对沿射线方向的点进行采样，并根据权积分对颜色进行累加。关于Eqn. 4和Eqn. 5的无偏和闭塞感知特性的详细离散化和证明，请参考我们的补充材料。

The choice of $\varsigma_{r}$ in $\tau_{r}$

尽管我们已经给出了 $\varsigma_{r}$ 应该满足的规则（Eq.6、Eq.7)，有一系列满足规则的函数。In the family, 所有函数都适用于UDF体绘制，因此我们对几种不同的候选函数进行验证，以检查每个函数的收敛能力进行网络优化，即在给定训练迭代中，网络收敛到最佳结果的函数。

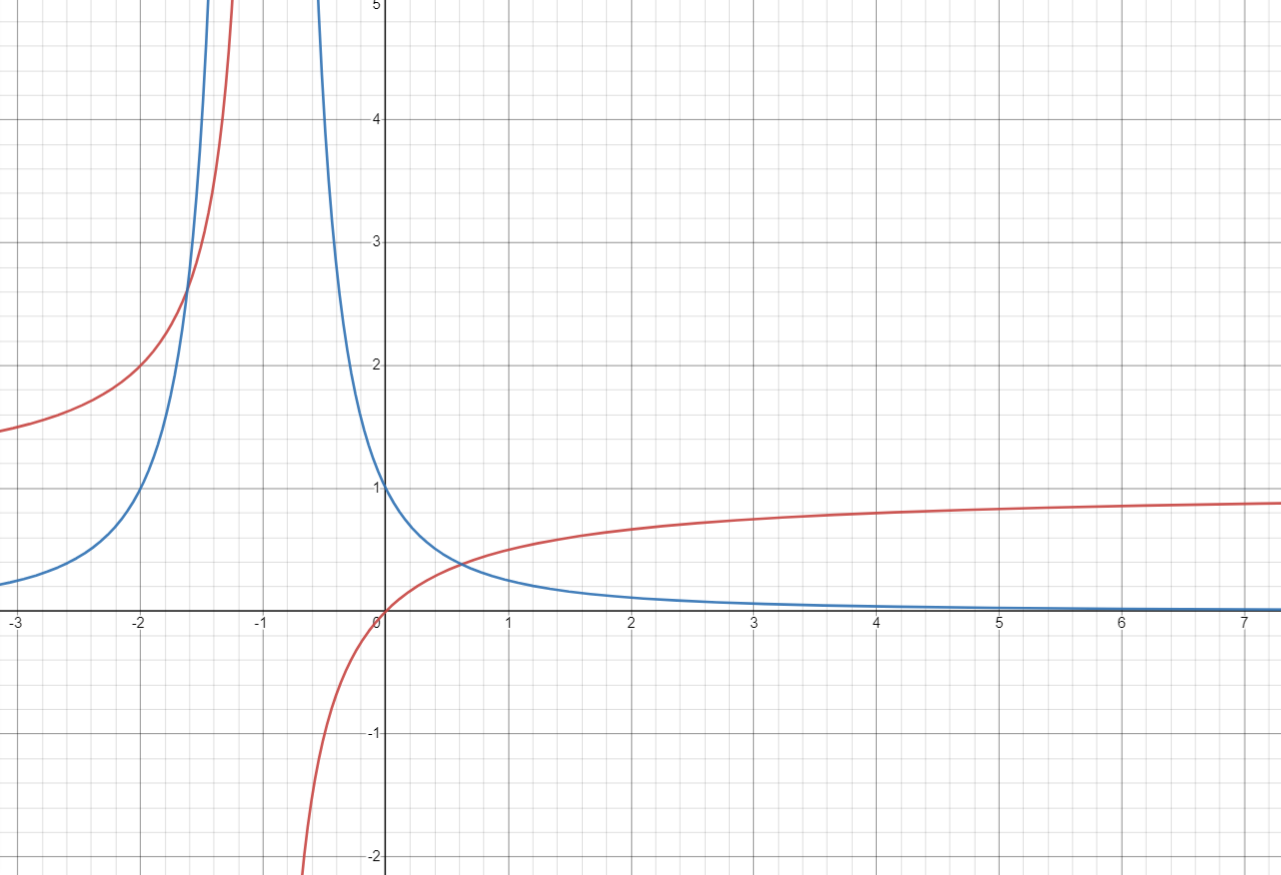
image.png
图 9 显示了遵循规则的三个候选函数$(1-e^{-x},\frac{2arctan(x)}\pi\text{ and }\frac x{1+x})$ 的视觉结果。在给定迭代(300k)之后，使用函数$\frac x{1+x}$的网络在定性和定量上都收敛到最佳结果，而其他函数不是完全收敛的，导致表面不完整，倒角距离略高。对不同形状的评估还表明，所有函数都运行良好，并且所选函数 $\frac x{1+x}$在我们的设置中效果最好（我们的：1.11 对 candidates：1.13/1.18）。

  • 红色：$\varsigma_{r}(d) = \frac x{1+x}$
  • 蓝色：$\varsigma_r^{\prime}(d) = \frac{1}{(1+x)^{2}}$
    image.png

Importance points sampling.

适应渲染权重的点采样是体绘制的重要步骤。与SDF不同，为了实现UDF的无偏渲染，渲染函数应该在交点前分配更多的权重(图2(c))。因此，如果渲染和采样函数都使用相同的权重，则UDF梯度的正则化(Eikonal损失)将导致表面两侧的梯度幅度高度不平衡。这可能会严重影响重建UDF field的质量。因此，我们提出了一个专门定制的采样权函数(图2(c))，以实现整个空间的良好平衡正则化。重要性抽样$w_{s}(t)$的公式为:$w_s(t)=\tau_s(t)e^{-\int_0^t\tau_s(u)du},\tau_s(t)=\zeta_s\circ\Psi\circ p(t),$ Eq.8

image.png

其中，$\zeta_{s}(\cdot)$满足以下规则:$\zeta_s(d)>0$且$\zeta_s^{\prime}(d) < 0$，$∀d > 0$。直观地说，$\zeta_{s}(\cdot)$在第一象限是一个单调递减的函数。在本文中，我们使用$\zeta_s(d)=\frac{se^{-sd}}{(1+e^{-sd})^2}$，其中$\zeta_{s}(d)$中的参数b控制x = 0处的强度。S从0.05开始，以$2^{z−1}$的速率改变每个采样步长z。任何可以与渲染函数实现平衡正则化的采样函数都与我们的框架兼容。有关上述规则的详细说明，请参阅我们的补充文件。此外，我们定性和定量地评估了在烧蚀研究中使用$\zeta_s(d)$的必要性(第4.3节)。

总体而言，在体绘制过程中，权重函数在渲染(Eqn. 4)和采样(Eqn. 8)中协同使用，实现了具有可微体绘制的高保真开放表面重建。

Normal Regularization

由于UDF的零水平集中的点不是一阶可微的顶点，因此在学习表面附近的采样点的梯度在数值上不是稳定的(抖动的)。由于绘制权函数以UDF梯度为输入，不可靠的梯度会导致曲面重建不准确。为了缓解这一问题，我们引入了正态正则化来执行空间插值。法向正则化用邻近的插值法向替换原始采样的表面法向。图4给出了一个详细的说明。

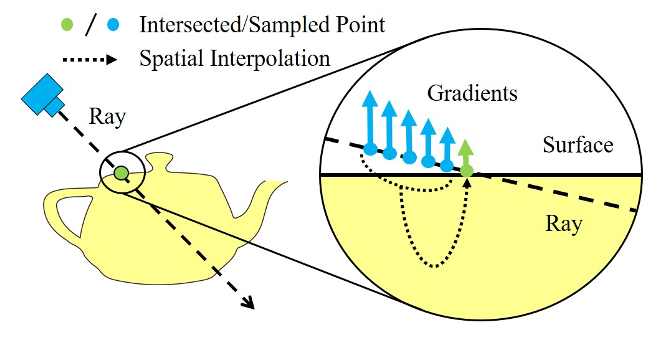
image.png
法向正则化图。我们使用与表面偏移的点的梯度(蓝色)来近似UDF表示的不稳定表面法线(绿色)。

由于不稳定法线只存在于曲面附近，我们使用与曲面有偏移的点法线来近似不稳定法线。我们在$p(t_i)$点离散地表示为:

$\mathbf{n}(p(t_i))=\frac{\sum_{k=1}^Kw_{i-k}\Psi^{\prime}(p(t_{i-k}))}{\sum_{k=1}^Kw_{i-k}}$ Eq.9

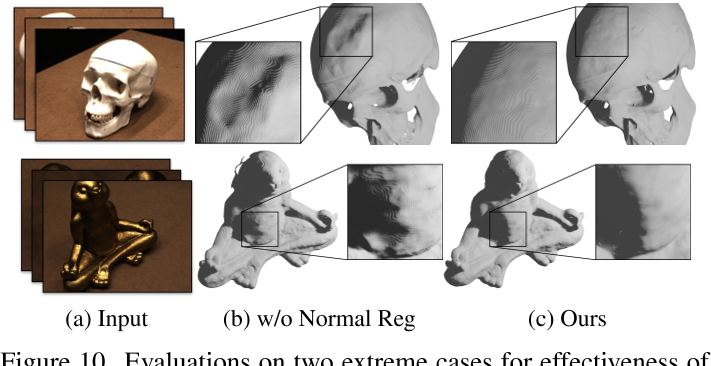
其中，$\begin{aligned}w_{i-k}=|p(i)-p(i-k)|_2^2\end{aligned}$是$p(i)$到$p(i-k)$的距离。$\Psi^{\prime}(\cdot)$是UDF $\Psi(\cdot)$的导数，返回UDF的梯度。通过利用法向正则化，我们的框架从2D图像中实现了更平滑的开放表面重建。我们可以调整法向正则化权值以获得更详细的几何形状。实验表明，法向正则化可以防止二维图像中高亮和高暗区域的高质量重建，如图10所示。

image.png

Training

为了学习高保真开放表面重建，我们在没有任何3D监督的情况下，通过最小化渲染图像和已知相机姿势的ground truth图像之间的差异来优化网络。继Neus[53]之后，我们还应用了SDF体绘制中使用的三个损失术语: 颜色损失$\mathcal{L}_{c}$, Eikonal损失[58]$\mathcal{L}_{e}$和Mask损失$\mathcal{L}_{m}$。

  • 颜色损失衡量的是L1损失下渲染图像与输入图像之间的差异。
  • Eikonal损失对采样点上的UDF梯度进行了数值正则化。
  • 如果提供了掩模，掩模损失也会促使预测掩模接近BCE测量下的真值掩模。

总的来说，我们使用的损失由三部分组成:

$\mathcal{L}=\mathcal{L}_{c}+\alpha\mathcal{L}_{e}+\beta\mathcal{L}_{m}$ Eq.10

实验和评估

Experimental Setup

Datasets

  • Multi-Garment Net数据集(MGN)[4]
  • Deep Fashion3D数据集(DF3D)[61]
  • DTU MVS数据集(DTU)[21]
    • 每个场景包含49或64张1600 × 1200分辨率的图像，蒙版来自IDR[58]。

Baselines

  • Colmap
  • IDR
  • Neus
  • NeuralWarp
  • HF-Neus

Metrics

  • Chamfer Distance (CD) to quantitative

Comparisons on Multi-view Reconstruction

  • Quantitative Results
  • Qualitative Results.
  • Captured Real Scenes

Further Discussions and Analysis

  • The choice of $\varsigma_{r}$ in $\tau_{r}$
  • Necessity of Importance Points Sampling
  • Necessity of Normal Regularization.

Welcome to my other publishing channels