NeuDA

Title	NeuDA: Neural Deformable Anchor for High-Fidelity Implicit Surface Reconstruction
Author	Bowen Cai ,Jinchi Huang, Rongfei Jia ,Chengfei Lv, Huan Fu*
Conf/Jour	CVPR
Year	2023
Project	NeuDA (3d-front-future.github.io)
Paper	NeuDA: Neural Deformable Anchor for High-Fidelity Implicit Surface Reconstruction (readpaper.com)

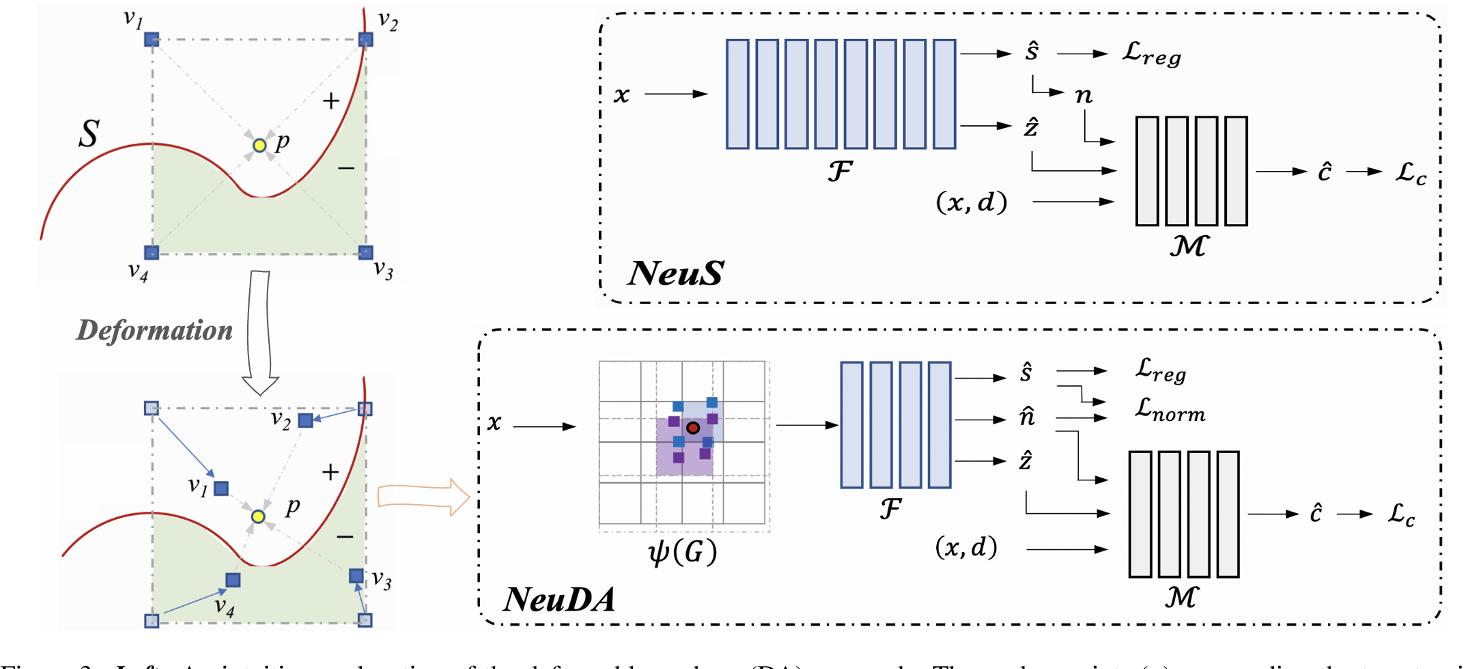
NeuDA变形后的grid距离Surface更近一些，即可以使采样点插值时更多依赖于表面，即渲染时也会更多地考虑到3D空间相邻的信息

创新：Deformable Anchors、HPE、$\mathcal{L}_{norm}$

• 改进了NGP中的grid表示，8个顶点存储feature—>存储锚点位置，锚点位置经过PE后输入进SDF网络

Discussion

One of the major limitations of this paper is that we follow an intuitive idea to propose NeuDA and conduct empirical studies to validate its performance. Although we can not provide strictly mathematical proof, we prudently respond to this concern and provide qualitative proof by reporting the anchor points’ deformation process in Figure 8.

Taking a slice of grid voxels as an example, we can see the anchor points (e.g. orange points) move to object surfaces as training convergences, resulting in an implied adaptive representation. Intuitively, the SDF change has an increasing effect on geometry prediction as the anchor approaches the surfaces, while the SDF change of a position far from the object has weak effects. Thus, the optimization process may force those anchors (“yellow” points) to move to positions nearly around the object surfaces to better reflect the SDF changes. The deformable anchor shares some similar concepts with deformable convolution [4] and makes its movement process like a mesh deformation process. Moreover, as each query point has eight anchors, from another perspective, each anchor follows an individual mesh deformation process. Thereby, NeuDA may play an important role in learning and ensembling multiple 3D reconstruction models.

直观地看，随着锚点接近物体表面，SDF变化对几何预测的影响越来越大，而远离物体位置的SDF变化对几何预测的影响较弱。

Conclusion

This paper studies neural implicit surface reconstruction. We find that previous works (e.g. NeuS) are likely to produce over-smoothing surfaces for small local geometry structures and surface abrupt regions. A possible reason is that the spatial context in 3D space has not been flexibly exploited. We take inspiration from the insight and propose NeuDA, namely Neural Deformable Anchors, as a solution. NeuDA is leveraging multi-level voxel grids, and is empowered by the core “Deformable Anchors (DA)“ representation approach and a simple hierarchical position encoding strategy.
The former maintains(DA) learnable anchor points at verities to enhance the capability of neural implicit model in handling complicated geometric structures, and
the latter(HPE) explores complementaries of high-frequency and low-frequency geometry properties in the multi-level anchor grid structure.
The comparisons with baselines and SOTA methods demonstrate the superiority of NeuDA in capturing high-fidelity typologies.

AIR

This paper studies implicit surface reconstruction leveraging differentiable ray casting. Previous works such as IDR [35] and NeuS [28] overlook the spatial context in 3D space when predicting and rendering the surface, thereby may fail to capture sharp local topologies such as small holes and structures.

To mitigate the limitation, we propose a flexible neural implicit representation leveraging hierarchical voxel grids, namely Neural Deformable Anchor (NeuDA), for high-fidelity surface reconstruction. NeuDA maintains the hierarchical anchor grids where each vertex stores a 3D position (or anchor) instead of the direct embedding (or feature). We optimize the anchor grids such that different local geometry structures can be adaptively encoded. Besides, we dig into the frequency encoding strategies and introduce a simple hierarchical positional encoding method for the hierarchical anchor structure to flexibly exploit the properties of high-frequency and low-frequency geometry and appearance. Experiments on both the DTU [8] and BlendedMVS [33] datasets demonstrate that NeuDA can produce promising mesh surfaces.

• 分层锚网格：每个顶点存储3D位置或者锚点，而不是特征值
• 引入一种简单的分层位置编码方式，灵活地利用高频和低频的几何和外观属性

3D surface reconstruction from multi-view images is one of the fundamental problems of the community. Typical Multi-view Stereo (MVS) approaches perform cross-view feature matching, depth fusion, and surface reconstruction (e.g., Poisson Surface Reconstruction) to obtain triangle meshes [9].Some methods have exploited the possibility of training end-to-end deep MVS models or employing deep networks to improve the accuracy of sub-tasks of the MVS pipeline.

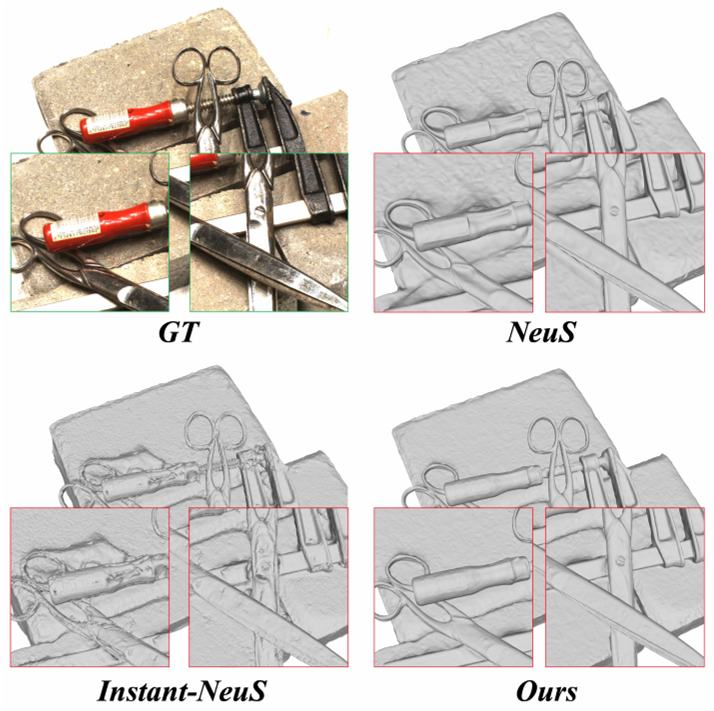
Neus 将物体表面定义为sdf的零水平集，but these methods have not explored the spatial context in 3D space.
As a result, they may struggle to recover fine-grain geometry in some local spaces, such as boundaries, holes, and other small structures

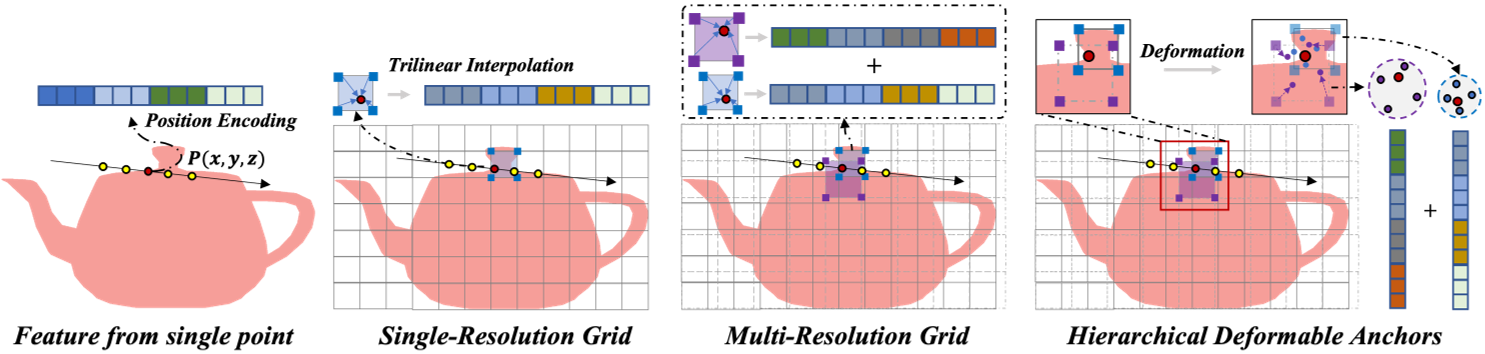
• A straightforward solution is to query scene properties of a sampled 3D point by fusing its nearby features.
  • For example, we can represent scenes as neural voxel fields where the embedding (or feature) at each vertex of the voxel encodes the geometry and appearance context.
  • Given a target point, we are able to aggregate the features of the surrounding eight vertices. As the scope of neighboring information is limited by the resolution of grids, multi-level (or hierarchical) voxel grids have been adopted to study different receptive fields. These approaches do obtain sharper surface details compared to baselines for most cases, （Multi res Hash grid）
  • but still cannot capture detailed regions well. A possible reason is that the geometry features held by the voxel grids are uniformly distributed around 3D surfaces, while small structures are with complicated typologies and may need more flexible representations

ours NeuDA:

• 代替多分辨率哈希网格中的每个顶点存取特征信息，NeuDA的每个网格顶点中存取的是3D点的位置/锚点信息，具体采样得到的3D点特征由，8个顶点坐标经过PE后，三线性插值频率嵌入得到。
  • The input feature for a query point is obtained by directly interpolating the frequency embedding of its eight adjacent anchors.
• we present a simple yet effective hierarchical positional encoding policy that adopts a higher frequency band to a finer grid level
• It’s worth mentioning that NeuDA employs a shallower MLP (4 vs. 8 for NeuS and volSDF) to achieve better surface reconstruction performance due to the promising scene representation capability of the hierarchical deformable anchor structure.

Related Work

• Neural Implicit Surface Reconstruction
  • NeRF—>Neus…
    • Nevertheless, the above approaches extract geometry features from a single point along a casting ray, which may hinder the neighboring information sharing across sampled points around the surface
  • It is worth mentioning that the Mip-NeRF 虽然使用锥形光线(tracing an anti-aliased conical frustum)进行采样，将相邻的信息带入渲染过程，但是由于位置编码依赖the radius of the casting cone.因此很难应用到surface reconstruction
• Neural Explicit Representation
  • Voxel和pointcloud等显式表示使得在模型优化过程中更容易将邻域信息注入到几何特征中
    • DVGO [25] and Plenoxels [23] represent the scene as a voxel grid, and compute the opacity and color of each sampled point via trilinear interpolation of the neighboring voxels.
    • The Voxurf [31] further extends this single-level voxel feature to a hierarchical geometry feature by concatenating the neighboring feature stored voxel grid from different levels.
    • The Instant-NGP [18] and MonoSDF [37] use multiresolution hash encoding to achieve fast convergence and capture high-frequency and local details, but they might suffer from hash collision due to its compact representation.
    • Both of these methods leverage a multi-level grid scheme to enlarge the receptive field of the voxel grid and encourage more information sharing among neighboring voxels. Although the voxel-based methods have further improved the details of surface geometry, they may be suboptimal in that the geometry features held by the voxel grids are uniformly distributed around 3D surfaces, while small structures are with complicated typologies and may need more flexible representation.
    • 但是体素方法斥候的几何特征均匀分布在3D表面，而微小的结构拥有复杂的typologies，需要更灵活的表示方法
    • Point-based methods [2, 12, 32] bypass this problem, since the point clouds, initially estimated from COLMAP [24], are naturally distributed on the 3D surface with complicated structures. Point-NeRF [32] proposes to model point-based radiance field, which uses an MLP network to aggregate the neural points in its neighborhood to regress the volume density and view-dependent radiance at that location. However, the point-based methods are also limited in practical application, since their reconstruction performance depends on the initially estimated point clouds that often have holes and outliers.
    • 点云的方法依赖初始估计的点云，这些点云通常具有孔洞和离群

Method

Preliminaries: Neus

Deformable Anchors (DA)

目的：提高体素网格表示的灵活性

• 从图中可以看出，NeuDA变形后的grid距离Surface更近一些，即可以使采样点插值时更多依赖于表面，即渲染时也会更多地考虑到3D空间相邻的信息

沿着特定光线上的采样点：$p\in\mathbb{R}^3$

$\begin{aligned}\phi(p,\psi(G))&=\sum_{v\in\mathcal{V}}w(p_v)\cdot\gamma(p_v+\triangle p_v),\\\psi(G)&=\left\{p_v,\triangle p_v|v\in G\right\}.\end{aligned}$

• G: anchor grid
• $\psi(G)$ ： a set of deformable anchors
• $\gamma(p_v+\triangle p_v)$: frequency encoding function
• $w(p_v)$: cosine similarity as weight , measure the contributions of different anchors to the sampled point
  • $w(p_{n})=\frac{\hat{w}(p_{n})}{\sum_{n}\hat{w}(p_{n})},\quad\hat{w}(p_{n})=\frac{p\cdot p_{n}}{|p||p_{n}|}.$

$\begin{aligned}\mathcal{F}(x;\theta)&=\mathcal{F}\left(\phi\left(p,\psi(G)\right);\theta\right)\\&=\left(f(x;\theta),\hat{n}(x;\theta),z(x;\theta)\right).\end{aligned}$

相比Neus，NeuDA具有

• HPE
• 法向损失$\mathcal{L}_{norm}$
• 更浅的MLP

Hierarchical Positional Encoding

several levels of anchor grid（8 levels in this paper）

• bad: applying the standard positional encoding function [17] to each level followed by a concatenation operation would produce a large-dimension embedding
• ours: We argue that different anchor grid levels could have their own responsibilities for handling global structures or capturing detailed geometry variations.

在水平L的网格中，给定锚点$p_{l}\in\mathbb{R}^3$，则the frequency encoding function: $\gamma(p_l)=\left(\sin(2^l\pi p_l),\cos(2^l\pi p_l)\right).$分别应用于$p_{l}$中的三个坐标值，然后每个L网格，经过interpolation operation返回a small 6-dimension embedding：$\phi(\hat{p}_{l})$

Finally, we concatenate multi-level embedding vectors to obtain the hierarchical positional encoding:

$\mathcal{H}(p)=(\phi(\hat{p}_0),\phi(\hat{p}_1),…,\phi(\hat{p}_{L-1})),$编码后的结果输入进SDF网络中

Objectives

We minimize the mean absolute errors between the rendered and ground-truth pixel colors as the indirect supervision for the SDF prediction function: 间接监督SDF的预测

$\mathcal{L}_{c}=\frac1{\mathcal{R}}\sum_{r\in\mathcal{R}}\Big|C(r)-\hat{C}(r)\Big|,$

Eikonal term：
$\mathcal{L}_{reg}=\frac{1}{\mathcal{R}N}\sum_{r,i}(|\nabla f(\mathcal{H}(p_{r,i}))|_{2}-1)^{2},$

$\mathcal{L}_{mask}=\mathrm{BCE}(m_r,\sum_i^nT_{r,i}\alpha_{r,i}),$

$m_{r}$是射线r的掩码标签，是真实值，与权重累计opacity(预测值)进行BCE处理

本文额外添加了一个：NeuDA的SDF网络还输出一个预测的法向量$\hat n$ ，与sdf的梯度即真实法向量进行取差，并沿着光线求出该像素点的法向量之差作为法向量损失

$\mathcal{L}_{norm}=\sum_{r,i}T_{r,i}\alpha_{r,i}\left|\nabla f(\mathcal{H}(p_{r,i}))-\hat{n}_{r,i}\right|$

$\mathcal{L}=\mathcal{L}_{c}+\lambda_{eik}\mathcal{L}_{reg}+\lambda_{norm}\mathcal{L}_{norm}+\lambda_{mask}\mathcal{L}_{mask}.$

本文：

• $\lambda_{eik}=0.1$
• $\lambda_{normal}=3 \times 10^{-5}$
• $\lambda_{mask}=0.1$