| Title | Improving neural implicit surfaces geometry with patch warping |
|---|---|
| Author | François Darmon1, 2 Bénédicte Bascle1 Jean-Clément Devaux1 Pascal Monasse2 Mathieu Aubry2 |
| Conf/Jour | 2022 |
| Year | CVPR |
| Project | Improving neural implicit surfaces geometry with patch warping |
| Paper | Improving neural implicit surfaces geometry with patch warping |
AIR
In this paper, we argue that this comes from the difficulty to learn and render high frequency textures with neural network. We thus propose to add to the standard neural rendering optimization a direct photo-consistency term across the different views. Intuitively, we optimize the implicit geometry so that it warps views on each other in a consistent way.
We demonstrate that two elements are key to the success of such an approach:
- (i) warping entire patches, using the predicted occupancy and normals of the 3D points along each ray, and measuring their similarity with a robust structural similarity (SSIM);
- (ii) handling visibility and occlusion in such a way that incorrect warps are not given too much importance while encouraging a reconstruction as complete as possible.
主要贡献:
• a method to warp patches using implicit geometry;
• a loss function able to handle incorrect reprojections;
• an experimental evaluation demonstrating the very significant accuracy gain on two standard benchmarks and validating each element of our approach.
Related Works
- Multi-view stereo (MVS)
- Neural implicit surfaces: UNISURF VolSDF NeuS
- Image warping and neural implicit surfaces:MVSDF
Method
Volumetric rendering of radiance field
The rendered color is approximated with an alpha blending of the point color $\mathbf{c}_{i}$:
$\mathbf{R}[\mathbf{p}]=\sum_{i=1}^N\alpha_i\prod_{j<i}(1-\alpha_j)\mathbf{c}_i,$
Warping images with implicit geometry
Pixel warping
使用 source image的投影来代替radiance network计算每个3D point 的颜色:
$\mathbf{W}_s[\mathbf{p}]=\sum_{i=1}^N\alpha_i\prod_{j<i}(1-\alpha_j)\mathbf{I}_s[\pi_s(\mathbf{x}_i)],$
$\mathbf{I}_s[\pi_s(\mathbf{x}_i)]$为使用3D点投影到$\mathbf{I}_{s}$上点颜色的双线性插值
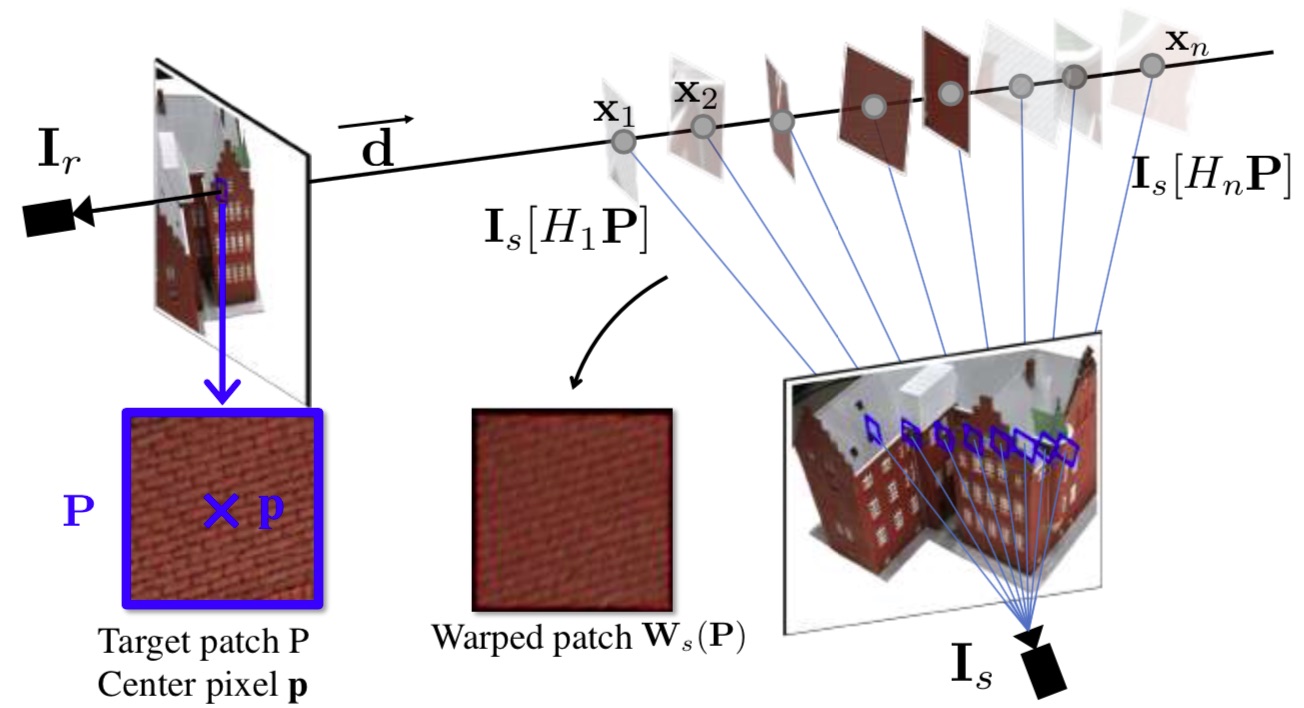
Patch warping
2D homogeneous coordinates: $H_{i}=K_{s}\left(R_{rs}+\frac{\mathbf{t}_{rs}\mathbf{n}_{i}^{T}R_{r}^{T}}{\mathbf{n}_{i}^{T}(\mathbf{x}_{i}+R_{r}^{T}\mathbf{t}_{r})}\right)K_{r}^{-1}$
$\mathbf{W}_s[\mathbf{P}]=\sum_{i=1}^N\alpha_i\prod_{j<i}(1-\alpha_j)\mathbf{I}_s[H_i\mathbf{P}]$
Optimizing geometry from warped patches
3D点投影时可能不在source image上,这种情况下$\mathbf{I}_s[H_i\mathbf{P}]$为NAN,本文使用一个constant padding color(gray color)代替
Warping-based loss:
$\mathcal{L}_{\mathrm{warp}}=\sum_{\mathbf{P}\in\mathcal{V}}\frac{\sum_{s\in\mathcal{S}}M_s[\mathbf{P}] d(\mathbf{I}_r[\mathbf{P}],\mathbf{W}_s[\mathbf{P}])}{\sum_{s\in\mathcal{S}}M_s[\mathbf{P}]}$
- $d$ 表示reference image 中patch的颜色与 wraped souce imaged 中 patch 颜色之间的photometric distance,使用SSIM进行计算
- $M_s[\mathbf{P}]\in[0,1]$ 表示为reference image 中patch对应的每个souce image 分配一个mask value
Validity masks: We now explain how we define the validity mask:
考虑导致wraps无效的两个原因:
- $M_s^\text{proj}[\mathbf{P}]=\sum_{i=1}^N\alpha_i\prod_{j<i}(1-\alpha_j)V_i^s$ the projection is not valid for geometric
reasons - $M_s^\text{occ}[\mathbf{P}]=T_s\left(\sum_{i=1}^N\alpha_i\prod_{j<i}(1-\alpha_j)\mathbf{x}_i\right)$ the patch is occluded by the reconstructed scene in the source image.