RayDF

Title	RayDF: Neural Ray-surface Distance Fields with Multi-view Consistency
Author	Zhuoman Liu, Bo Yang
Conf/Jour	NeurIPS
Year	2023
Project	RayDF: Neural Ray-surface Distance Fields with Multi-view Consistency (vlar-group.github.io)
Paper	RayDF: Neural Ray-surface Distance Fields with Multi-view Consistency (readpaper.com)

Abstract

本文研究了连续三维形状表示问题。现有的成功方法大多是基于坐标的隐式神经表示。然而，它们在呈现新视图或恢复显式表面点方面效率低下。一些研究开始将三维形状表述为基于光线的神经函数，但由于缺乏多视图几何一致性，学习到的结构较差。
为了应对这些挑战，我们提出了一个名为 RayDF 的新框架。它包括三个主要部分:
1)简单的射线-表面距离场，
2)新颖的双射线可见性分类器，
3)多视图一致性优化模块，以驱动学习的射线-表面距离在多视图几何上一致。
我们在三个公共数据集上广泛评估了我们的方法，证明了在合成和具有挑战性的现实世界3D 场景中3D 表面点重建的显着性能，明显优于现有的基于坐标和基于光线的基线。最值得注意的是，我们的方法在渲染800 × 800深度的图像时，速度比基于坐标的方法快1000倍，显示了我们的方法在3D 形状表示方面的优势。我们的代码和数据可在 https://github.com/vLAR-group/RayDF上获得

Method

Overview

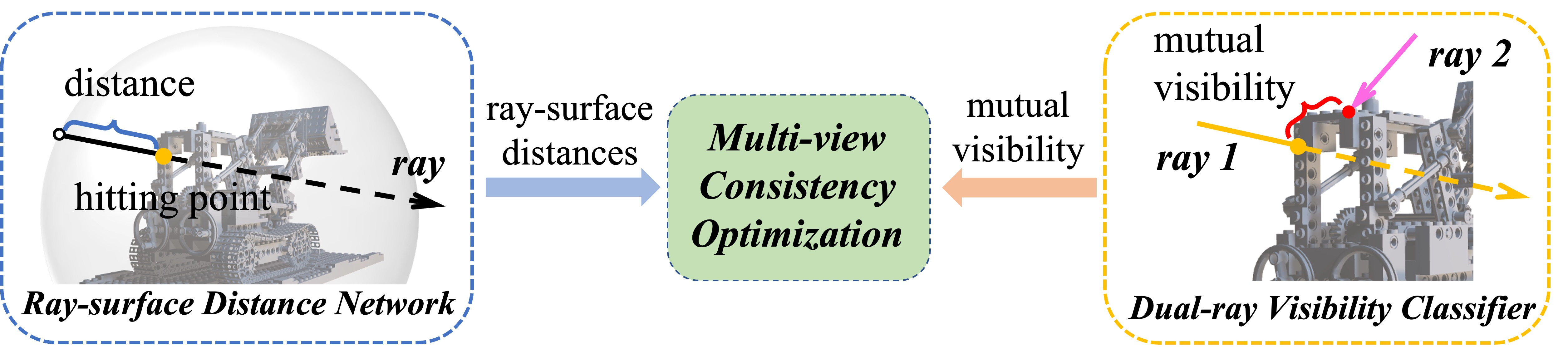
两个网络+一个优化模块

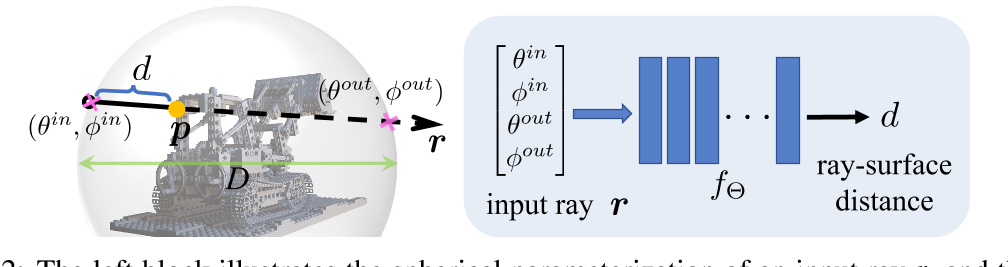
• 主网络 ray-surface distance field $f_{\mathbf{\Theta}}$
  • 输入：单条定向射线 r 使用球形化参数射线，每条射线穿过球体有两个交点，每个交点有两个变量参数化(相对于球体中心的角度)，i.e. $r=(\theta^{in},\phi^{in},\theta^{out},\phi^{out}),$
  • 输出：射线起点与表面落点之间的距离 d
• 辅助网络 dual-ray visibility classifier $h_{\Phi}$
  • 输入：一对射线
  • 输出：相互可见性，旨在显式地建模任意一对射线之间的相互空间关系。主要用于第三部分的多视图一致性优化

Dual-ray Visibility Classifier

单独的 ray-surface distance field 也可以拟合输入输出，但没有机制驱动其输出距离，即表面几何。i.e.缺乏多视图一致性

下图中的 $r_1$ 和 $r_2$ 相互可见，则两条光线同时击中一个表面点。则应该满足：
$\left.r_1^{in}+d_1r_1^d=\left(\begin{smallmatrix}x_1\\y_1\\z_1\end{smallmatrix}\right.\right)=r_2^{in}+d_2r_2^d,\mathrm{~where~}r^d=\frac{r^{out}-r^{in}}{\left|\boldsymbol{r}^{out}-\boldsymbol{r}^{in}\right|}$ $\left.\mathrm{and~}r^=\left(\begin{array}{c}\sin\theta^\cos\phi^\\\sin\theta^\sin\phi^\\\cos\phi^\end{array}\right.\right),*\in\{in,out\}$

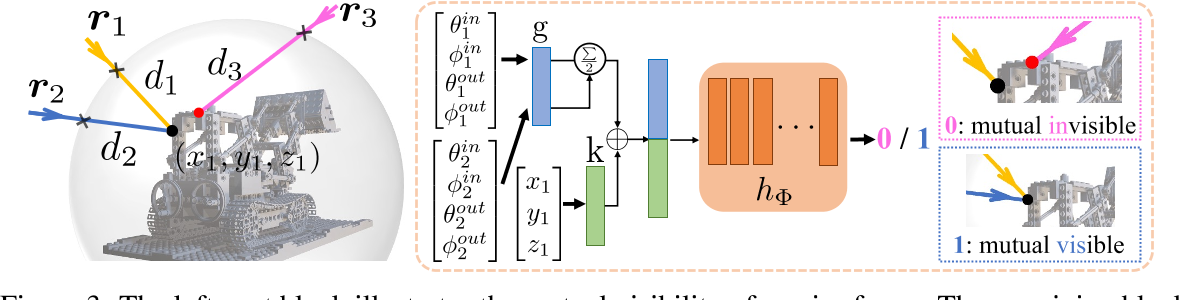
任意两条射线之间的相互可见性 mutual visibility 对于 ray-surface distance field 的多视图一致性至关重要

dual-ray visibility classifier 二元分类器设计需要保证即便两个射线的顺序调换，也可以得到相同的结果

$h_{\Phi}:\quad MLPS\Big[\frac{g(\theta_1^{in},\phi_1^{in},\theta_1^{out},\phi_1^{out})+g(\theta_2^{in},\phi_2^{in},\theta_2^{out},\phi_2^{out})}2\oplus k(x_1,y_1,z_1)\Big]\to0/1$

• G(): 一个共享的单一全连接层

Multi-view Consistency Optimization

给定一个静态 3D 场景的 K 张深度图像(H × W)作为整个训练数据，训练模块由两个阶段组成

Stage 1 - Training Dual-ray Visibility Classifier
首先，将所有原始深度值转换为射线表面距离值。对于第 K 张图像中的特定第 i 条射线(像素)，我们将其射线表面点投影回剩余的(K−1)次扫描，获得相应的(K−1)个距离值。我们设置 10 毫米作为接近阈值，以确定投影(K−1)射线在(K−1)图像中是否可见。总的来说，我们生成了 K∗H∗W∗(K−1)对带有 0/1 标记的射线。采用标准交叉熵损失函数对双射线可见性分类器进行优化

请注意，这个分类器是以特定于场景的方式进行训练的。一旦网络得到良好的训练，它基本上会将特定场景的任意两条光线之间的关系编码为网络权重。

Stage 2 - Training Ray-surface Distance Network
我们整个管道的最终目标是优化 Ray-surface Distance Network，并使其具有多视图几何一致性。然而，这不是微不足道的，因为简单地用射线表面数据点拟合网络不能推广到看不见的射线，这可以在我们第 4.5 节的消融研究中看到。在这方面，我们充分利用训练良好的可见性分类器来帮助我们训练射线表面距离网络。具体而言，这一阶段包括以下关键步骤:

• 所有深度图像都转换为射线表面距离，为特定的 3D 场景生成 K H W 训练射线距离对。
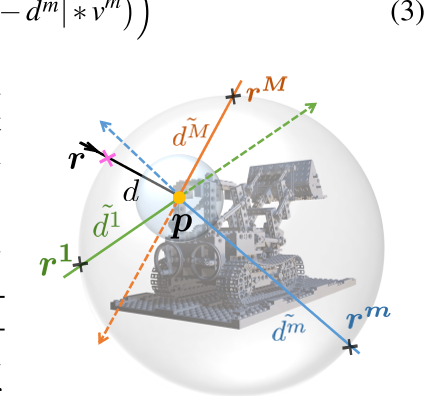
• 如图4所示，对于特定的训练射线 $(r,d)$，称为主射线，我们在以表面点 p 为中心的球内均匀采样 M 条射线 $\{r^1\cdots r^m\cdots r^M\}$，称为多视图射线。然后，我们沿着每条 M rays 计算表面点 p 与边界球之间的距离，得到多视图距离 $\{\tilde{d}^{1}\cdots\tilde{d}^{m}\cdots\tilde{d}^{M}\}.$ 根据训练集中给定的距离 d，这很容易实现。M 简单地设置为20，更多细节见附录A.4。
• 我们建立 M 对射线 $\left\{(r,p,r^1)\cdots(r,p,r^m)\cdots(r,p,r^M)\right\}$，然后将它们输入到训练良好的可见性分类器 $h_{\Phi}$ 中，推断出它们的可见性得分 $\{\nu^1\cdots\nu^m\cdots\nu^M\}.$。
• 我们 feed 主光线采样 M 多视点射线 $\{r,r^1\cdots r^m\cdots r^M\}$ 到 ray-surface distance network $f_{\mathbf{\Theta}}$,估算其表面距离 $\{\hat{d},\hat{d^1}\cdots\hat{d^m}\cdots\hat{d^M}\}.$。由于网络 $f_{\mathbf{\Theta}}$ 是随机初始化的，因此一开始估计的距离是不准确的。
• 我们设计了以下多视图一致性损失函数来优化ray-surface distance network直至收敛:$\ell_{m\nu}=\frac1{\sum_{m=1}^M\nu^m+1}\Big(|\hat{d}-d|+\sum_{m=1}^M\left(|\hat{d}^m-\tilde{d}^m|*\nu^m\right)\Big)$

基本上，这种简单的损失驱动网络不仅要拟合主要的射线-表面距离(训练集中的可见射线)，而且要满足可见多视图射线(训练集中的无限未见射线)也具有准确的距离估计。

Surface Normal Derivation and Outlier Points Removal

在上述3.1&3.2&3.3章节中，我们有两个网络设计和一个优化模块分别对它们进行训练。然而，我们的经验发现，主要的射线-表面距离网络可能预测不准确的距离值，特别是对于锐利边缘附近的射线。从本质上讲，这是因为在极端视角变化的情况下，实际的射线表面距离在尖锐边缘处可能是不连续的。这种形状不连续实际上是几乎所有现有的隐式神经表示的共同挑战，因为现代神经网络在理论上只能对连续函数建模。

幸运的是，我们的射线-表面距离场的一个很好的性质是，每个估计的三维表面点的法向量可以很容易地用网络的自微分推导出一个封闭形式的表达式。特别地，给定一条输入射线$r=(\theta^{in},\phi^{in},\theta^{out},\phi^{out}),$以及它到网络$f_{\mathbf{\Theta}}$的估计射线-曲面距离d，则该估计曲面点对应的法向量n可以推导为如下所示的具体函数: $n=Q\left(\frac{\partial\hat{d}}{\partial r},r,D\right)$

有了这个法向量，我们可以选择添加一个额外的损失来正则化估计的表面点，使其尽可能光滑。然而，我们从经验上发现，整个3D场景的整体性能提升是相当有限的，因为这些极端不连续的情况实际上是稀疏的。

在这方面，我们转向简单地去除预测的表面点，即离群点，其法向量的欧几里得距离大于网络推理阶段的阈值。实际上，PRIF[23]也采用了类似的策略来过滤掉异常值。请注意，先进的平滑或插值技术可以集成来改进我们的框架，这将留给未来的探索。

Experiments

我们的方法在三种类型的公共数据集上进行了评估:
1)来自原始NeRF论文[47]的对象级合成Blender数据集，
2)来自最近DM-NeRF论文[73]的场景级合成DM-SR数据集，
3)场景级真实世界的ScanNet数据集[16]。

基线:我们精心选择了以下六个成功且具有代表性的隐式神经形状表示作为我们的基线:1)OF [46]， 2) DeepSDF [54]， 3) NDF [14]， 4) news [77]， 5) DSNeRF [19]， 6) LFN [64]， 7) PRIF[23]。
OF/DeepSDF/NDF/NeuS方法是基于坐标的水平集方法，在三维结构建模中表现出优异的性能。
DS-NeRF是一种深度监督的NeRF[47]，继承了2D视图渲染的优秀能力。
LFN和PRIF是两种基于光线的方法，在生成二维视图方面效率较高。
我们注意到，这些基线有许多复杂的变体，可以在各种数据集上实现SOTA性能。然而，我们并不打算与它们进行全面的比较，主要是因为它们的许多技术，如更高级的实现、添加额外的条件、替换更强大的骨干等，也可以很容易地集成到我们的框架中。我们将这些潜在的改进留给未来的探索，但在本文中只关注我们的香草射线表面距离场。为了公平的比较，所有基线都与我们的深度扫描量相同，以相同的场景特定方式从头开始仔细训练。关于所有基线的实施和可能的小调整的更多细节见附录A.3.1。

Conclusion

在本文中，我们已经证明，通过使用多视图一致的基于光线的框架，有效和准确地学习3D形状表示是真正可能的。与现有的基于坐标的方法相比，我们使用简单的射线-表面距离场来表示三维几何形状，并进一步由一种新的双射线可见性分类器驱动，以实现多视图形状一致。在多个数据集上的大量实验证明了我们的方法具有极高的渲染效率和出色的性能。用更高级的技术(如更快的实现和额外的正则化)扩展我们的框架会很有趣。

实验

环境配置

创建虚拟环境

conda create -n raydf python=3.8 -y
conda activate raydf

问题：

• 在wsl2中配置好pip install torch==1.12.1+cu113 torchvision==0.13.1+cu113 --extra-index-url https://download.pytorch.org/whl/cu113 和 pip install -r requirements.txt后发现cuda无法使用
  • JAX: 库安装和GPU使用，解决不能识别gpu问题_jax安装_Papageno2018的博客-CSDN博客
• 转到win10中配置，发现jax和jaxlib的0.4.10版本无法安装到python3.8中
  • jaxlib暂不支持windows_jaxlib-0.3.20+cuda11.cudnn82-cp38-cp38-win_amd64.w_GoldMinnie的博客-CSDN博客

==环境配置失败2023.11.14~11.16==