NeRO

Title	NeRO: Neural Geometry and BRDF Reconstruction of Reflective Objects from Multiview Images
Author	Yuan Liu, Peng Wang, Cheng Lin, Xiaoxiao Long, Jiepeng Wang, Lingjie Liu, Taku Komura, Wenping Wang
Conf/Jour	SIGGRAPH 2023
Year	2023
Project	NeRO: Neural Geometry and BRDF Reconstruction of Reflective Objects from Multiview Images (liuyuan-pal.github.io)
Paper	NeRO: Neural Geometry and BRDF Reconstruction of Reflective Objects from Multiview Images (readpaper.com)

Reference

[PDF] NeRD: Neural Reflectance Decomposition From Image Collections
[PDF] SAMURAI: Shape And Material from Unconstrained Real-world Arbitrary Image collections
[PDF] Relighting4D: Neural Relightable Human from Videos
[PDF] Neural 3D Scene Reconstruction with the Manhattan-world Assumption
[PDF] NeROIC: Neural Rendering of Objects from Online Image Collections

对金属反光材质的物体重建效果很好

提出了一种新的光表示方法，颜色由漫反射和镜面反射两部分组成，通过两个阶段的方法来实现

• Stage1：使用集成方向编码来近似光积分，使用shadow MLP对直接光和间接光进行model，学习到了表面几何形状
• Stage2：蒙特卡罗采样固定几何形状，重建更精确的表面BRDF和环境光
  • $\mathbf{c}_{\mathrm{diffuse}}=\frac{1}{N_{d}}\sum_{i}^{N_{d}}(1-m)\mathrm{a}L(\omega_{i}),$
  • $\mathbf{c}_{\mathrm{specular}}=\frac{1}{N_{s}}\sum_{i}^{N_{s}}\frac{FG(\omega_{0}\cdot\mathbf{h})}{(\mathbf{n}\cdot\mathbf{h})(\mathbf{n}\cdot\omega_{\mathbf{0}})}L(\omega_{i}),$

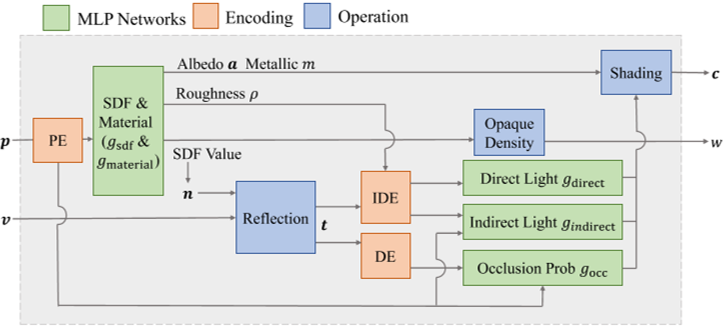
Stage1 MLP：

• SDF&Material：
  • input: p2PE
  • output: Albedo , Metallic , Roughness, SDF
• Refection计算：SDF2n法向量 , v观察方向 —> t反射方向
• Direct Light：
  • input: Roughness&t to IDE
  • output: shading
• Indirect Light: 间接光与球空间中的位置有关
  • input: Roughness&t to IDE , p2PE
  • output: shading
• Occlusion Prob: 来确定在渲染中将使用直接灯光还是间接灯光
  • input: t2DE, p2PE
  • output: shading
• Opaque Density计算：SDF —> w权重
• Shading计算： Albedo , Metallic , shading —> c颜色
  • Light integral approximation ， 由 $g_{direct}$输出、$g_{indirect}$输出和遮挡概率s(t)计算出光积分
  • 由漫射光积分、镜面反射光积分、反照率a和金属度m计算出最终该点的颜色

$$\begin{gathered} \mathbf{c}(\omega_{0})=\mathbf{c}_{\mathrm{diffuse}}+\mathbf{c}_{\mathrm{specular}}, \\ \mathbf{c}_{\mathrm{diffuse}}=\int_{\Omega}(1-m)\frac{\mathbf{a}}{\pi}L(\omega_{i})(\omega_{i}\cdot\mathbf{n})d\omega_{i}, \\ \mathbf{c}_{\mathrm{specular}}=\int_{\Omega}\frac{DFG}{4(\omega_{i}\cdot\mathbf{n})(\omega_{0}\cdot\mathbf{n})}L(\omega_{i})(\omega_{i}\cdot\mathbf{n})d\omega_{i}. \end{gathered}$$

光近似：
$\mathbf{c}_{\mathrm{diffuse}}=\text{a}(1-m)\underbrace{\int_{\Omega}L(\omega_{i})\frac{\omega_{i}\cdot\mathbf{n}}{\pi}d\omega_{i},}_{L_{\mathrm{diffuse}}}$
$\mathbf{c}_{\mathrm{specular}}\approx\underbrace{\int_{\Omega}L(\omega_{i})D(\rho,\mathbf{t})d\omega_{i}}_{L_{\mathrm{specular}}}\cdot\underbrace{\int_{\Omega}\frac{DFG}{4(\omega_{0}\cdot\mathbf{n})}d\omega_{i},}_{M_{\mathrm{specular}}}$
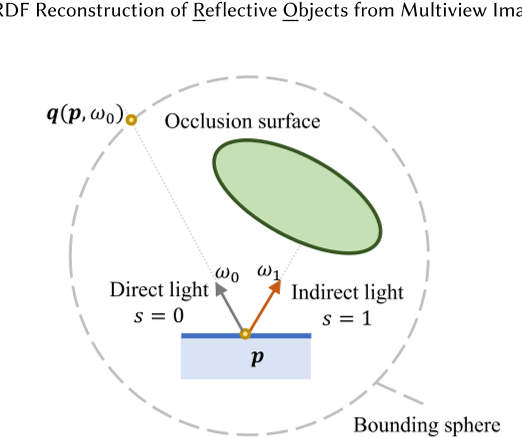
其中亮度可以分为直接光(outer sphere)和间接光(inner sphere)

$$\begin{aligned} L_{\mathrm{specular}}&\approx[1-s(\mathrm{t})]\int_{\Omega}g_{\mathrm{direct}}(SH(\omega_l))D(\rho,\mathrm{t})d\omega_l+\\&s(\mathrm{t})\int_{\Omega}g_{\mathrm{indirect}}(SH(\omega_l),\mathrm{p})D(\rho,\mathrm{t})d\omega_l\\&\approx[1-s(\mathrm{t})]g_{\mathrm{direct}}(\int_{\Omega}SH(\omega_l)D(\rho,\mathrm{t})d\omega_l)+\\&s(\mathrm{t})g_{\mathrm{indirect}}(\int_{\Omega}SH(\omega_i)D(\rho,\mathrm{t})d\omega_l,\mathrm{p}). \end{aligned}$$

• 优点
  • 不需mask，主要目标是重建物体的几何形状和BRDF的颜色
• 不足
  • 几何中的细节无法重建出来（太光滑）
  • 由于颜色依赖法向量估计，表面法线的错误会导致难以拟合正确的颜色
  • 依赖于准确的输入相机姿势，并且估计反射物体上的相机姿势通常需要稳定的纹理，如用于图像匹配的校准板。
  • 很慢，在3090(24G)上，Stage1的隐式重建需要大概10个小时左右，Stage2的BRDF色彩重建需要3个半小时左右

纹理校准板

Conclusion

我们提出了一种神经重建方法NeRO，它可以在不知道环境光照条件和物体掩模的情况下精确地重建反射物体的几何形状和BRDF。NeRO的关键思想是明确地将渲染方程合并到神经重构框架中。
NeRO通过提出一种新颖的光表示和采用两阶段方法来实现这一具有挑战性的目标。

• 在第一阶段，通过应用易于处理的近似，我们用阴影mlp对直接和间接光进行建模，并忠实地学习表面几何形状。
• 在第二阶段，我们通过蒙特卡罗采样固定几何形状，重建更精确的表面BRDF和环境光。

实验表明，与最先进的技术相比，NeRO可以实现更好的表面重建质量和反射物体的BRDF估计。

AIR

我们提出了一种基于神经渲染的方法，称为NeRO，用于从未知环境中捕获的多视图图像中重建反射物体的几何形状和BRDF

BRDF: 双向反射分布函数 The bidirectional reflectance distribution function
Bidirectional reflectance distribution function - Wikipedia

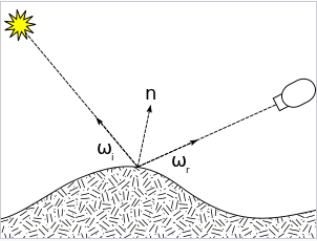
${\displaystyle f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\,=\,{\frac {\mathrm {d} L_{\text{r}}(\omega _{\text{r}})}{\mathrm {d} E_{\text{i}}(\omega _{\text{i}})}}\,=\,{\frac {1}{L_{\text{i}}(\omega _{\text{i}})\cos \theta _{\text{i}}}}{\frac {\mathrm {d} L_{\text{r}}(\omega _{\text{r}})}{\mathrm {d} \omega _{\text{i}}}}}$

反射物体的多视图重建非常具有挑战性，因为镜面反射依赖于视图，从而违反了多视图一致性，而多视图一致性是大多数多视图重建方法的基础。
最近的神经渲染技术可以模拟环境光和物体表面之间的相互作用，以适应与视图相关的反射，从而使从多视图图像中重建反射物体成为可能。然而，在神经渲染中，环境光的精确建模是一个棘手的问题，特别是在几何形状未知的情况下。现有的神经渲染方法对环境光进行建模时，大多只考虑直射光，依靠物体蒙版来重建反射较弱的物体。因此，这些方法无法重建反射物体，特别是在没有物体掩模和物体被间接光照射的情况下。

我们建议采取两步走的办法来解决这个问题。

• 首先，通过应用分割和近似split-sum approximation和集成方向编码来近似直接和间接光的阴影效果，我们能够准确地重建反射物体的几何形状，而不需要任何物体遮罩。
• 然后，在物体几何形状固定的情况下，我们使用更精确的采样来恢复物体的环境光和BRDF。大量的实验表明，我们的方法能够在不知道环境光和物体掩模的情况下，仅从RGB图像中准确地重建反射物体的几何形状和BRDF。

Introduction

• Multiview 3D reconstructionreconstruction，a fundamental task in computer graphics and vision近年来取得了巨大进步[Oechsle et al. 2021;Schönberger等。2016;Wang等。2021 a, b;姚等人。2018;Yariv等。2021,2020]。
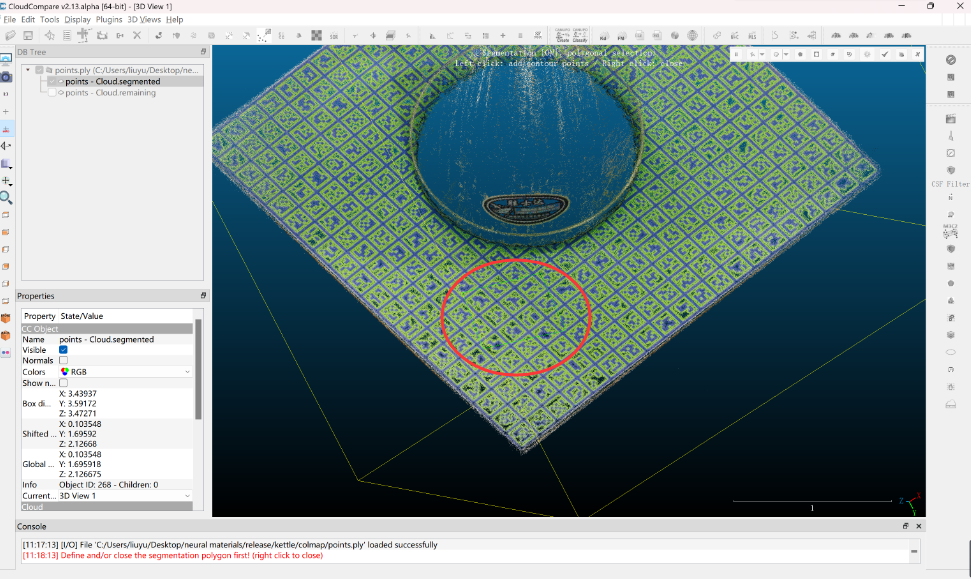
  • 尽管取得了令人信服的成果，但在现实环境中经常看到的反射物体的重建仍然是一个具有挑战性和突出的问题。反光物体通常有光滑的表面，部分或全部照射在物体上的光被反射。当从不同的角度观察物体时，反射导致颜色不一致。然而，大多数多视图重建方法严重依赖于视图一致性来进行立体匹配。这对现有技术的重建质量构成了重大障碍。图2 (b)显示了广泛使用的COLMAP [Schönberger et al. 2016]在反射物体上的重建
• 作为多视图重建的新兴趋势，基于神经渲染的曲面建模显示出处理复杂物体的强大能力[Oechsle等人。2021;Wang等。2021 b;Yariv等人。2021年,2020]。在这些所谓的神经重建方法中，底层表面几何被表示为隐式函数，例如，由多层感知(MLP)编码的符号距离函数(SDF)。为了重建几何图形，这些方法通过建模与视图相关的颜色并最小化渲染图像与输入图像之间的差异来优化神经隐式函数。
  • 然而，神经重建方法仍然难以重建反射物体。图2 (c)给出了示例。原因是这些方法中使用的颜色函数只将颜色与视图方向和表面几何形状关联起来，而没有明确考虑反射的底层遮阳机制。因此，拟合表面上不同视角方向的镜面颜色变化会导致错误的几何形状，即使在位置编码中频率更高，或更深更宽的MLP网络。
• 为了解决具有挑战性的表面反射，我们建议明确地将渲染方程的公式[Kajiya 1986]纳入神经重建框架。渲染方程使我们能够考虑表面双向反射分布函数(BRDF) [Nicodemus 1965]与环境光之间的相互作用。由于反射物体的外观受到环境光线的强烈影响，因此依赖于视图的镜面反射可以用渲染方程很好地解释。通过显式渲染函数，大大增强了现有神经重构框架的表征能力，以捕获高频镜面颜色变化，从而显著有利于反射物体的几何重建。
• 显式地将渲染方程合并到神经重建框架中并不是微不足道not trivial.的。在未知的表面位置和未知的环境光下，计算环境光的积分是一个棘手的问题。
  • 为了可跟踪地评估渲染方程，现有的材料估计方法[Boss等]。[2021 a, b;Hasselgren et al. 2022;Munkberg等人。2022;Verbin et al. 2022;Zhang等。2021a,b, 2022b]强烈依赖物体掩模来获得正确的表面重建，主要用于无强镜面反射的物体的材料估计，在反射物体上的效果要差得多，如图2 (d,e)所示。此外，这些方法大多进一步简化了渲染过程，只考虑来自遥远区域的光(直射光)[Boss等]。2021 a, b;Munkberg et al. 2022;Verbin等。2022;Zhang等。[2021a]，因此很难重建被物体本身或附近区域(间接光)的反射光照射的表面。虽然有方法[Hasselgren et al. 2022;Zhang et al. 2021b, 2022b]考虑到渲染中的间接光，它们要么需要具有已知几何形状的重建辐射场[Zhang et al. 2021b];2021b, 2022b]或只使用很少的射线样本来计算光[Hasselgren等。2022]，这会导致对反射对象的不稳定收敛或对对象掩模的额外依赖。因此，同时考虑直接光和间接光来正确重建反射物体的未知表面仍然是一个挑战。
• 通过将渲染方程整合到神经重建框架中，我们提出了一种称为NeRO的方法，用于仅从RGB图像中重建反射物体的几何形状和BRDF。NeRO的关键组成部分是一种新颖的光表示。在这种光表示中，我们使用两个单独的mlp分别编码直接光和间接光的亮度，并计算遮挡概率以确定在渲染中应该使用直接光还是间接光。这样的光表示有效地适应了直射光和间接光，以精确地重建反射物体的表面。基于提出的光表示，NeRO采用两阶段策略对神经重建中的渲染方程进行易于处理的评估。
  • NeRO的第一阶段采用分割和近似和集成方向编码[Verbin等人。2022]来评估渲染方程，该方程可以在折衷compromised的环境光和表面BRDF估计的情况下产生精确的几何重建。
  • 然后，在重建几何固定的情况下，NeRO的第二阶段通过蒙特卡罗采样更准确地评估渲染方程来改进估计的BRDF。
  • 通过光表示和两阶段设计，该方法从本质上扩展了神经渲染方法对反射物体的表示能力，使其充分发挥了学习几何表面的潜力。
• 为了评估NeRO的性能，我们引入了一个合成数据集和一个真实数据集，这两个数据集都包含被复杂环境光照射的反射物体。在这两个数据集上，NeRO都成功地重建了反射物体的几何和表面BRDF，而基线MVS方法和神经重建方法都失败了。我们的方法的输出是一个带有估计BRDF参数的三角形网格，可以很容易地用于下游应用，如重照明。

RELATED WORKS

• Multiview 3D reconstruction（MVS）
  • 多视角三维重建或多视角立体(MVS)已经研究了几十年。传统的多视图重建方法主要依靠三维点的多视图一致性来建立对应关系并估计不同视图上的深度值。随着深度学习技术的进步，最近的许多研究[Cheng et al .2020;Wang等。2021年;Yan等。2020;Yang et al. 2020;姚等人。2018]尝试引入神经网络来估计MVS任务的对应关系，这在广泛使用的基准测试中展示了令人印象深刻的重建质量[Geiger等人。2013;Jensen等人。2014;Scharstein and Szeliski 2002]。
  • 在本文中，我们的目标是重建具有强镜面反射的反射物体。强烈的镜面反射违背了多视图一致性，因此这些基于对应的方法在反射对象上表现不佳。
  • Neural surface reconstruction神经渲染和神经表示因其强大的表征能力和对新视图合成任务的显著改进而备受关注。
    • DVR [Niemeyer et al. 2020]首次在多视图重建中引入了神经渲染和神经表面表示。
    • IDR [Yariv et al. 2020]通过可微球追踪和Eikonal正则化[Gropp et al. 2020]提高了重建质量。
    • UNISURF [Oechsle等]。VolSDF [Yariv et al. 2021]和Neus [Wang et al. 2021 2021b]在多视图表面重建中引入了可微体绘制，提高了鲁棒性和质量。随后的工作在各个方面改进了基于体渲染的多视图重建框架，例如引入曼哈顿或正常先验[Guo等. 2022b;Wang等。2022c]，利用对称性[Insafutdinov et al. 2022;Zhang等。2021c]，提取图像特征[damon et al. 2022;Long et al. 2022]，提高保真度[Fu et al. 2022;Wang等。2022b]和效率[Li et . 2022;Sun et al. 2022;Wang等。2022年;Wu等人。2022;赵等。2022a]。
    • 与这些工作类似，我们也遵循体绘制框架进行表面重建，但我们的重点是重建具有强镜面反射的反射物体，这是现有神经重建方法尚未探索的突出问题。
• Reflective object reconstruction
  • 只有少数作品试图通过使用额外的物体遮罩来重建多视图立体环境中的反射物体[Godard等人。2015]或去除反射[Wu等。2018]。
  • 除了不受控制的多视图重建，一些作品[Han et al. 2016;Roth and Black 2006]采用已知镜面流的约束设置[Roth and Black 2006]或已知环境[Han等。2016]用于重建理想的镜面物体。
  • 其他一些工作通过编码射线来利用额外的射线信息[Tin等]或利用偏振图像[Dave et al. 2022;Kadambi et al. 2015;Rahmann and Canterakis 2001]用镜面反射来重建物体。
  • [Whelan et al. 2018]利用扫描仪的反射图像重建场景中的镜像平面。
  • 这些方法被限制在一个相对严格的设置与特殊设计的捕获设备。相比之下，我们的目标是直接从多视图图像中重建反射物体，这些图像可以很容易地用手机相机捕捉到。
  • 一些基于图像的渲染方法[Rodriguez et al .2020;Sinha et al. 2012]是专门为NVS任务设计的光滑或反射物体。
  • NeRFRen [Guo等 2022a]重构了存在镜像平面的场景的神经密度场。
  • 神经点溃散学[Kopanas et al .2022]应用翘曲场来提高反射物体的渲染质量。
  • Ref-Nerf [Verbin et al .][2022]提出了集成方向编码(IDE)来提高反射材料的NVS质量。
  • 我们的方法结合了IDE来重建反射物体，并使用神经SDF进行表面重建。一个并行的工作ORCA [Tiwary et al. 2022]扩展到从光滑物体上的反射重建场景的辐射场，这也重建了管道中的物体。由于ORCA的目标主要是重建场景的亮度场，因此它依赖于物体蒙版来重建反射物体。相比之下，我们的方法不需要物体遮罩，我们的主要目标是重建物体的几何形状和BRDF。
• BRDF estimation
  • 从图像中估计地表BRDF主要基于逆渲染技术[Barron and Malik 2014;Nimier-David等人。2019]。
  • 一些方法[Gao et . 2019;郭等。2020;Li等人。2020年,2018年;温鲍尔等人，2022;叶等人。2022]在直接估计BRDF和照明之前依赖于物体或场景。
  • 可微分渲染器Differentiable renderers[Chen et al. 2019,2021;Kato et al. 2018;Liu et al. 2019;Nimier-David等人。2019]允许从图像损失中直接优化BRDF。为了获得更准确的BRDF估计，大多数方法[Bi et al .2020年,(无日期);Cheng等。2021;Kuang et al. 2022;李和李2022a,b;Nam等人。2018;Schmitt et al. 2020;Yang等。2022a,b;Zhang等人2022a]要求物体的多个图像由不同的组合手电筒照射。
  • 在本文中，我们估计了带有移动摄像机的静态场景中的BRDF，这也是Boss等人采用的设置[2021a, 2022, 2021b;Deng et al. 2022;Hasselgren等人。2022;Munkberg et al. 2022;张等。2021a,b, 2022b]。
  • 其中，PhySG [Zhang等 2021a]， NeRD [Boss等 2021a]，神经网络- pil [Boss等 2021b]和NDR [Munkberg et al. 2022]在BRDF估计中考虑了直接环境光与表面之间的相互作用。后续工作MII[张等 2022b]， NDRMC [Hasselgren等。2022]，DIP [Deng等 2022]和NeILF [Yao等 2022]增加间接照明，这提高了估计BRDF的质量
  • 这些方法的主要目的是重建普通物体的BRDF，避免太多的镜面反射，从而在反射物体上产生低质量的BRDF。其他一些方法[Chen and Liu 2022;Duchêne et al. 2015;Gao等。2020;Liu等人。2021;Lyu等人。2022;Nestmeyer等人。2020;菲利普等人。2019年,2021年;Rudnev等人。2022;Shih et al. 2013;你等人。2020;Yu and Smith 2019;赵等，2022b;Zheng等人2021]主要针对重光照任务，而不是为重建表面几何或BRDF而设计的。
  • NeILF [Yao et al. 2022]与我们方法的第二阶段最相似，两者都固定了几何形状，以通过MC采样优化BRDF。然而，NeILF没有对镜面瓣进行重要采样，只是从一个位置和一个方向预测光线，而不考虑遮挡。相比之下，我们的方法明确区分直接和间接光，并在漫反射和镜面上使用重要采样，以便更好地估计反射物体的BRDF。

METHOD

Overview

给定一组已知相机姿势的RGB图像作为输入，我们的目标是重建图像中反射物体的表面和BRDF。注意，我们的方法不需要知道物体遮罩或环境光。
NeRO的pipeline由两个阶段组成

• 在第一阶段(3.3节)，我们通过优化带有体渲染的神经SDF来重建反射物体的几何形状，其中估计近似的直接和间接光来模拟依赖于视图的镜面颜色。
• 在第二阶段(第3.4节)，我们固定了物体的几何形状，并微调了直接和间接光，以计算反射物体的精确BRDF。

我们首先简要回顾一下Neus [Wang et al. 2021b]和微观面BRDF模型[Cook and Torrance 1982;托伦斯和斯派洛1967]

我们遵循Neus，用MLP网络编码的SDF来表示物体表面。$g_{sdf}(x)$，曲面为${x∈R^{3} |\mathcal{g}_{sdf} (x) = 0}$。然后，将体绘制[Mildenhall et al. 2020]应用于从神经SDF中渲染图像。给定相机光线$o+tv$从相机中心沿方向发射到空间，我们采样射线上的点$\{\mathbf{p}_{j}=\mathbf{o}+t_{j}\mathbf{v}|t_{j}>0,t_{j-1}<t_{j}\}.$。然后，计算这个相机光线的渲染颜色

$\hat{\mathbf{c}}=\sum_{n}w_{j}\mathbf{c}_{j},$

权重w通过[Wang et al. 2021b]中提出的不透明密度从SDF值导出的。c是这个点的颜色，由MLP网络输出得到$\mathbf{c}_{j}=g_{\mathrm{color}}(\mathbf{p}_{j},\mathbf{v})$。然后，通过最小化渲染颜色c与gt的c之间的差异，两个MLP网络的参数是train得到的。$g_{sdf}$的零水平集提取重构曲面。为了使颜色函数能够正确地表示反射表面上的高光颜色，NeRO使用Micro-facet BRDF将NeuS的颜色函数替换为阴影函数

Micro-facet BRDF: 点$p_j$的输出颜色
$\mathbf{c}(\omega_{0})=\int_{\Omega}L(\omega_{i})f(\omega_{i},\omega_{0})(\omega_{i}\cdot\mathbf{n})d\omega_{i},$

• $\omega_{o}= -v$ 是外观察方向，$c(\omega_o)$是外观察方向上电$p_j$的颜色
• $\mathbf{n}$是表面法向量
• $\omega_i$是输入光方向on the upper half sphere Ω,
• BRDF function：$f(\omega_{i},\omega_{0}) \in [0,1]^{3}$
• $L(\omega_{i}) \in [0,+\infty)^3$ 是入射光的亮度
• 在NeRO中，法向n是从SDF的梯度计算的。BRDF函数由漫反射部分和镜面部分组成

$$f(\omega_{i},\omega_{0})=\underbrace{(1-m)\frac{a}{\pi}}_{\mathrm{diffuse}}+\underbrace{\frac{DFG}{4(\omega_{i}\cdot\mathbf{n})(\omega_{0}\cdot\mathbf{n})}}_{\mathrm{specular}},$$

• $m \in [0,1]$: the metalness of the point
• 1-m为漫反射部分的权重
• $a \in [0,1]^3$:点的反照率颜色the albedo color of the point
• 𝐷 is the normal distribution function,
• 𝐹 is the Fresnel term
• 𝐺 is the geometry term
  • 𝐷, 𝐹 and 𝐺 are all determined by the metalness 𝑚 , the roughness $𝜌 ∈ [0, 1]$ and the albedo a
• 该点的BRDF由金属度、粗糙度和反照率决定，all of which are predicted by a material MLP $𝑔_{material}$ in NeRO, i.e., $[𝑚, 𝜌, a] = 𝑔_{material} (p).$

i.e: 颜色值

$$\begin{gathered} \mathbf{c}(\omega_{0})=\mathbf{c}_{\mathrm{diffuse}}+\mathbf{c}_{\mathrm{specular}}, \\ \mathbf{c}_{\mathrm{diffuse}}=\int_{\Omega}(1-m)\frac{\mathbf{a}}{\pi}L(\omega_{i})(\omega_{i}\cdot\mathbf{n})d\omega_{i}, \\ \mathbf{c}_{\mathrm{specular}}=\int_{\Omega}\frac{DFG}{4(\omega_{i}\cdot\mathbf{n})(\omega_{0}\cdot\mathbf{n})}L(\omega_{i})(\omega_{i}\cdot\mathbf{n})d\omega_{i}. \end{gathered}$$

如前所述，准确评估体绘制中每个样本点的漫反射和镜面反射颜色的积分是棘手的。因此，我们提出了一个两步框架来近似计算这两个积分。在第一阶段，我们的首要任务是忠实地重建几何表面。

Stage I: Geometry reconstruction

为了重建反射物体的表面，我们采用了与Neus[Wang et al. 2021b]相同的神经SDF表示和体绘制算法(Eq. 1)，但使用了不同的颜色函数。在NeRO中，我们预测金属度、粗糙度和反照率使用微面BRDF来计算颜色。为了在Neus的体绘制中使计算易于处理，我们采用了分割和近似[Karis and Games 2013]，它将灯光和BRDF积的积分分离为两个单独的积分。

镜面反射颜色

$\mathbf{c}_{\mathrm{specular}}\approx\underbrace{\int_{\Omega}L(\omega_{i})D(\rho,\mathbf{t})d\omega_{i}}_{L_{\mathrm{specular}}}\cdot\underbrace{\int_{\Omega}\frac{DFG}{4(\omega_{0}\cdot\mathbf{n})}d\omega_{i},}_{M_{\mathrm{specular}}}$

• $L_{specular}$是光在正态分布函数上的积分$D(\rho,\mathbf{t}) \in [0,1]$, specular lobe
  • t : is the reflective direction
• $M_{specular}$为BRDF的积分

请注意，粗糙的表面有较大的镜面瓣，而光滑的表面有较小的镜面瓣。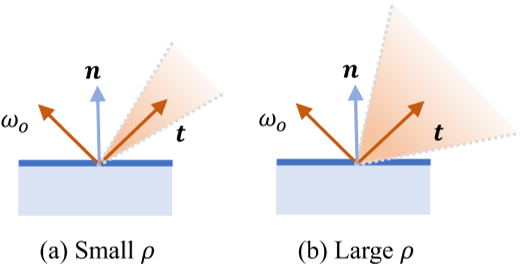

BRDF的积分可以由$\begin{aligned}M_{\mathrm{specular}}=((1-m)0.04+m\mathrm{a})*F_1+F_2,\end{aligned}$直接计算

• where 𝐹1 and 𝐹2 are two pre-computed scalars depending on the roughness 𝜌

漫反射颜色

The diffuse color：
$\mathbf{c}_{\mathrm{diffuse}}=\text{a}(1-m)\underbrace{\int_{\Omega}L(\omega_{i})\frac{\omega_{i}\cdot\mathbf{n}}{\pi}d\omega_{i},}_{L_{\mathrm{diffuse}}}$

$L_{diffuse}$为漫射光积分

由材料MLP预测的m,$\rho$,a。唯二未知的量为两个光积分
然而，为了计算光积分，我们不像以前的方法那样对环境光进行预滤波[Boss等。2021 b;Munkberg等人。2022]但使用集成定向编码[Verbin等人。2022]。

光表示Light representation

在NeRO中，我们在对象周围定义一个边界球来构建神经SDF。由于我们只重建边界球内的表面，所以我们将所有来自边界球外的光称为直接光，而将边界球内表面反射的光称为间接光，如图4所示。

$L(\omega_i)=[1-s(\omega_i)]g_\text{direct}(SH(\omega_i))+s(\omega_i)g_\text{indirect}(SH(\omega_i),\text{p}),$

• 两个mlp分别用于直接光和间接光：$g_{direct}, g_{indirect}$.这样所有的点都被相同的直接环境光照亮。这在解释反射对象的依赖于视图的颜色之前提供了一个强大的global
• 由于间接光在空间中变化，因此附加一个点位置p作为输入

Light integral approximation

我们使用集成方向编码来近似光积分

$$\begin{aligned} L_{\mathrm{specular}}&\approx[1-s(\mathrm{t})]\int_{\Omega}g_{\mathrm{direct}}(SH(\omega_l))D(\rho,\mathrm{t})d\omega_l+\\&s(\mathrm{t})\int_{\Omega}g_{\mathrm{indirect}}(SH(\omega_l),\mathrm{p})D(\rho,\mathrm{t})d\omega_l\\&\approx[1-s(\mathrm{t})]g_{\mathrm{direct}}(\int_{\Omega}SH(\omega_l)D(\rho,\mathrm{t})d\omega_l)+\\&s(\mathrm{t})g_{\mathrm{indirect}}(\int_{\Omega}SH(\omega_i)D(\rho,\mathrm{t})d\omega_l,\mathrm{p}). \end{aligned}$$

在第一个近似中，我们使用遮挡概率𝑠(t)以替换不同光线的遮挡概率𝑠 (𝜔𝑖 )。在第二近似中，我们交换MLP的阶数和积分
我们只需要评估MLP网络$𝑔_{direct}$和$𝑔_{indirect}$积分方向编码$\int_{\Omega}SH(\omega_i)D(\rho,\mathrm{t})d\omega_l$一次

通过选择正态分布函数𝐷 是von Mises–Fisher（vMF）分布（球面上的高斯分布）, Ref-NeRF已经展示了$\int_{\Omega}SH(\omega_i)D(\rho,\mathrm{t})d\omega_l$有一个近似闭合形式的解，在这种情况下，我们在这里使用这个闭合形式的解来近似光的积分。

类似地，对于漫反射光积分，
$\frac{\omega_i\cdot\mathbf{n}}\pi\approx D(1.0,\mathbf{n}).$

请注意，分裂和近似和光积分近似仅在第一阶段使用，以实现易于处理的计算，并将在第二阶段被更准确的蒙特卡罗采样所取代。

Occlusion loss

在灯光表示中，我们使用的遮挡概率𝑠 由MLP$𝑔_{occ}$预测来确定在渲染中将使用直接灯光还是间接灯光。然而，如图5所示，如果我们不对遮挡概率𝑠施加约束，并且让MLP网络从渲染loss中学习𝑠，预测的遮挡概率将与重建的几何结构完全不一致，并导致不稳定的收敛。

因此，我们使用神经SDF来约束预测的遮挡概率。给定从采样点p发射到其反射方向t的光线，我们计算其遮挡概率$s_{march}$在神经SDF中by ray-marching，并执行计算概率$s_{march}$和the predicted probability 𝑠之间的一致性$\ell_{occ}=|s_{\mathrm{march}}-s|_{1},$为遮挡概率正则化的损失

Training Losses

我们计算相机光线的颜色并计算Charbonier损失，在渲染颜色和输入地真颜色之间作为渲染损失(渲染损失)

同时，我们观察到SDF的前几个训练步骤是不稳定的，要么是极大地扩大了表面，要么是把表面压得太小。在前1k步中应用稳定化正则化损失。$\ell=\ell_\text{render}+\lambda_\text{eikonal}\ell_\text{eikonal}+\lambda_\text{occ}\ell_\text{occ}+1\text{(step}<1000)\ell_\text{stable},$

我们也采用Eikonal损失[Gropp等人。2020]将SDF梯度的范数正则化为1

Reflection of the capturer

在我们的模型中，我们假设一个静态照明环境。然而，在现实中，总是有一个人拿着相机捕捉周围反射物体的图像。移动的人会在物体的反射中可见，这就违反了静态照明的假设，如图7 (a)的红圈所示。

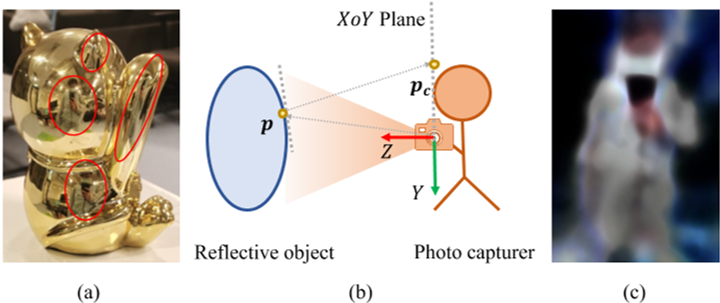
由于照片捕捉器相对于相机是静态的，我们在XoY平面建立了一个2D NeRF在摄像机坐标系中
在计算直射光时，我们还检查光线是否击中，如果hit点$p_{c}$存在，则使用$g_{camera}$，$[\alpha_{\mathrm{camera}},\mathrm{c}_{\mathrm{camera}}]=g_{\mathrm{camera}}(\mathrm{p}_{\mathrm{c}}),$来计算$\alpha_{camera}$和颜色

• $\alpha_{camera}$指示光线是否被捕获器遮挡
• $\mathrm{c}_{\mathrm{camera}}$表示该点上捕获器的颜色
• 然后，直射光是$(1-\alpha_{\mathrm{camera}})g_{\mathrm{direct}}(\omega_{i})+ \alpha_{camera} c_{camera}$

Stage II: BRDF estimation

到目前为止，在第一阶段之后，我们已经忠实地重建了反射物体的几何形状，但只得到了一个粗略的BRDF估计，需要进一步细化。在第二阶段，我们的目标是准确地评估渲染方程，从而精确地估计表面BRDF，即金属度、反照率和粗糙度。有了第一阶段的固定几何体，我们只需要在表面点上计算渲染方程。因此，现在可以应用蒙特卡罗采样来计算公式5中的漫射颜色和公式6中的镜面颜色。在MC采样中，我们对漫反射瓣和反射瓣都进行了重要采样。

• Importance sampling

  • 在蒙特卡洛采样中，漫反射颜色c漫反射是通过用余弦加权半球概率对射线进行采样来计算的$\mathbf{c}_{\mathrm{diffuse}}=\frac{1}{N_{d}}\sum_{i}^{N_{d}}(1-m)\mathrm{a}L(\omega_{i}),$
  • 𝑖 是第i个样本射线和$𝜔_{𝑖}$是此采样光线的方向。
  • 对于镜面反射颜色C，我们将GGX分布应用为正态分布𝐷. 然后，通过DDX分布的射线采样$𝑁_{𝑠}$条光线来计算镜面颜色$c_{specular}$ [Cook和Torrance1982]$\mathbf{c}_{\mathrm{specular}}=\frac{1}{N_{s}}\sum_{i}^{N_{s}}\frac{FG(\omega_{0}\cdot\mathbf{h})}{(\mathbf{n}\cdot\mathbf{h})(\mathbf{n}\cdot\omega_{\mathbf{0}})}L(\omega_{i}),$
  • 其中 h 是 𝜔𝑖 和 𝜔𝑜 之间的半向向量。为了评估上述两个式子我们仍然使用与第一阶段相同的材料 MLP [𝑚, 𝜌, a] = $g_{material}$来计算金属度 𝑚、粗糙度和反照率 a。第二阶段的灯表示$𝐿(𝜔_𝑖)$与第一阶段相同。由于几何是固定的，我们通过跟踪给定几何中的光线而不是从 MLP 中预测它来直接计算遮挡概率。同时，对于真实数据，我们在沿方向𝜔从p发出沿p的射线的边界球体$q_{p,𝜔}$上添加交点，如图4所示，作为直接轻MLP$𝑔_{direct}$的附加输入。

• Regularization terms

  • $\ell_{\mathrm{smooth}}=|g_{\mathrm{material}}(\mathrm{p})-g_{\mathrm{material}}(\mathrm{p}+\epsilon)|_{2},$
  • $\ell_{\mathrm{light}}=\sum_{c}^{3}([L_{\mathrm{diffuse}}]_{C}-\frac{1}{3}\sum_{c}^{3}[L_{\mathrm{diffuse}}]_{C}),$
  • $\ell=\ell_{\mathrm{render}}+\lambda_{\mathrm{smooth}}\ell_{\mathrm{smooth}}+\lambda_{\mathrm{light}}\ell_{\mathrm{light}},$

Limitations

几何。虽然我们成功地重建了反射物体的形状，但我们的方法仍然无法捕获一些细微的细节，如图19所示。主要原因是渲染函数强烈依赖于神经SDF估计的表面法线，但神经SDF往往会产生平滑的表面法线。因此，神经 SDF 很难产生突然的正常变化来重建细微的细节，例如“Angel”的布料纹理、“Cat”的胡子和“Maneki”的纹理。

BRDF。在实验中，我们观察到我们的BRDF估计主要存在不正确的几何形状，特别是在“Angel”上，如图20所示。由于反射物体的外观强烈依赖于表面法线来计算反射方向，表面法线的错误会使我们的方法难以拟合正确的颜色，从而导致BRDF估计不准确。同时，NeRO中的BRDF不支持各向异性反射等高级反射。

姿态估计。另一个限制是我们的方法依赖于准确的输入相机姿势，并且估计反射物体上的相机姿势通常需要稳定的纹理，如用于图像匹配的校准板。没有校准板，我们可以从其他共同可见的非反射物体或在IMU等设备的帮助下恢复姿势。

数据集

https://connecthkuhk-my.sharepoint.com/:f:/g/personal/yuanly_connect_hku_hk/EvNz_o6SuE1MsXeVyB0VoQ0B9zL8NZXjQQg0KknIh6RKjQ?e=jCLH0W

实验

环境配置

AutoDL:

• pytorch 1.11.0
• Python 3.8(ubuntu20.04)
• Cuda 11.3

pip install

• nvdiffrast.
• raytracing

git clone https://github.com/liuyuan-pal/NeRO.git
cd NeRO
pip install -r requirements.txt
-i https://pypi.tuna._tsinghua_.edu.cn/simple

# nvdiffrast
git clone https://github.com/NVlabs/nvdiffrast
pip install .

# raytracing
git clone https://github.com/ashawkey/raytracing
cd raytracing
pip install .

pip install --upgrade protobuf
pip install trimesh

运行

liuyuan-pal/NeRO: [SIGGRAPH2023] NeRO: Neural Geometry and BRDF Reconstruction of Reflective Objects from Multiview Images (github.com)

data: Models and datasets all can be found here.

NeRO
|-- data
    |-- GlossyReal
        |-- bear 
            ...
    |-- GlossySynthetic
        |-- bell
            ...

Stage 1 重建shape

训练程序获取隐式模型：

# reconstructing the "bell" of the Glossy Synthetic dataset
python run_training.py --cfg configs/shape/syn/bell.yaml

# reconstructing the "bear" of the Glossy Real dataset
python run_training.py --cfg configs/shape/real/bear.yaml

Intermediate results will be saved at data/train_vis. Models will be saved at data/model.

data/model/bear_shape

• (tensorboard logs_dir)logs: events.out.tfevents.1690871015.autodl-container-6a4811bc52-8879d78f
• model_best.pth —> model_dir = /data/model/bear_shape
• model.pth —> model_dir = /data/model/bear_shape
• train.txt —> logs_dir = (/data/model/bear_shape —> /root/tf-logs)
• val.txt —> logs_dir

tensorboard —> train/loss 40k step左，240k step右

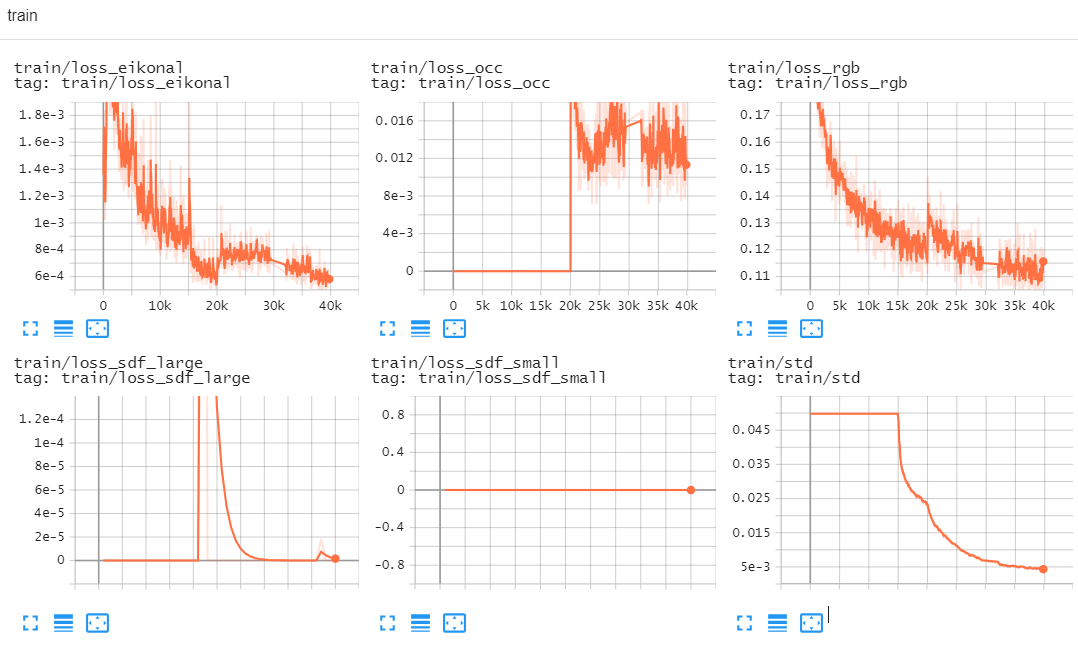
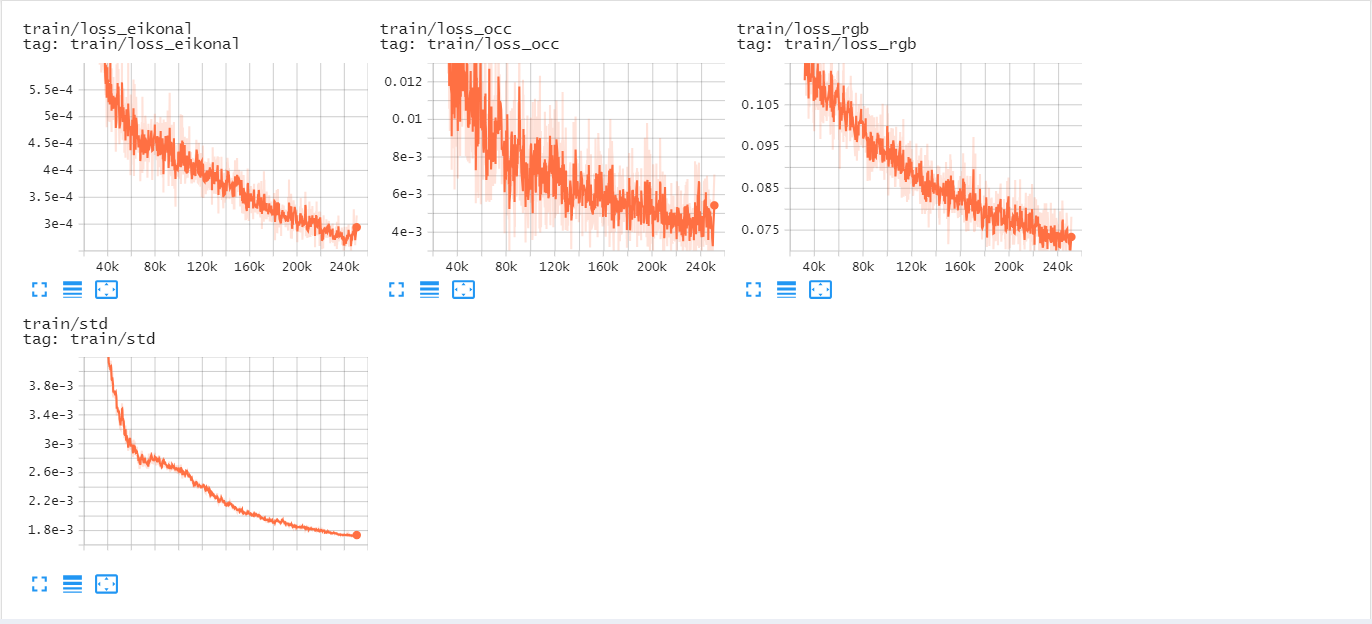
data/train_vis/bear_shape-val —> 14999-index-0.jpg左，244999-index-0.jpg右

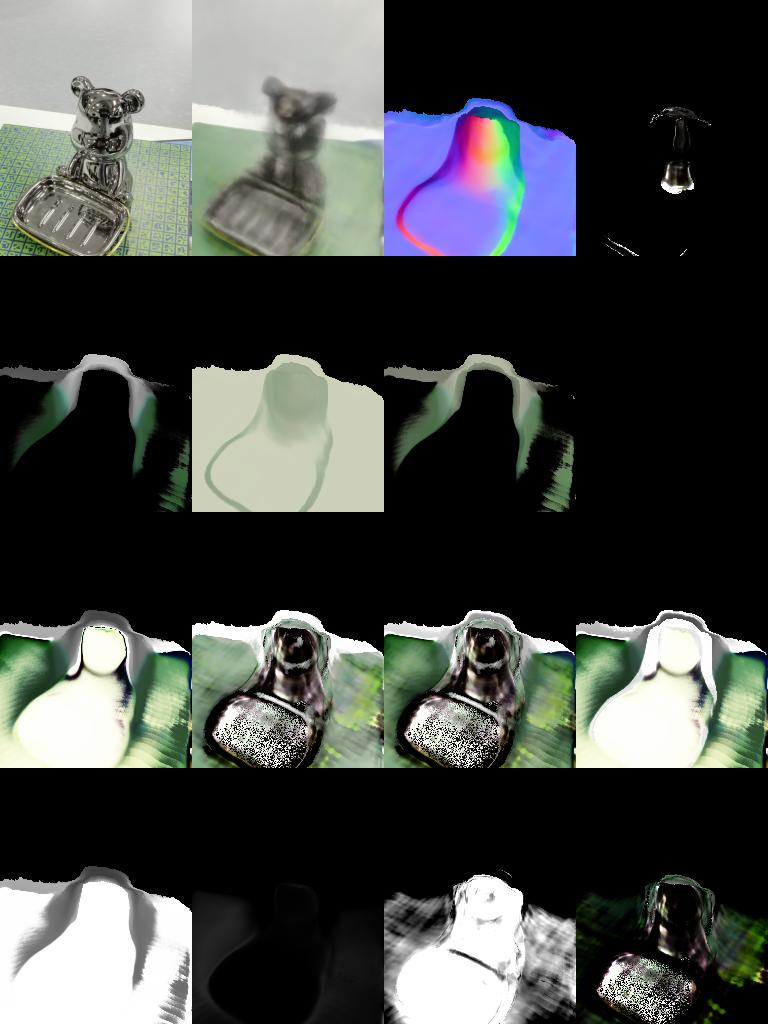
Extract mesh from the model.

python extract_mesh.py --cfg configs/shape/syn/bell.yaml
python extract_mesh.py --cfg configs/shape/real/bear.yaml

The extracted meshes will be saved at data/meshes.

bug: 
(nero) root@autodl-container-6a4811bc52-8879d78f:~/autodl-tmp/NeRO# python extract_mesh.py --cfg confi  
gs/shape/real/bear.yaml  
successfully load bear_shape step 300000!  
/root/miniconda3/lib/python3.8/site-packages/torch/functional.py:568: UserWarning: torch.meshgrid: in  
an upcoming release, it will be required to pass the indexing argument. (Triggered internally at ../a  
ten/src/ATen/native/TensorShape.cpp:2228.)  
return _VF.meshgrid(tensors, **kwargs) # type: ignore[attr-defined]

将return _VF.meshgrid(tensors, **kwargs) # type: ignore[attr-defined]
修改为return _VF.meshgrid(tensors, **kwargs, indexing = ‘ij’) # type: ignore[attr-defined]，警告解除
————————————————

应该是torch版本不匹配，亲测有效，不再出现UserWarning
————————————————
版权声明：本文为CSDN博主「余幼时即嗜学^」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_45103604/article/details/124717008

Stage 2 Material estimation or texture

ply mesh data

NeRO
|-- data
    |-- GlossyReal
        |-- bear 
            ...
    |-- GlossySynthetic
        |-- bell
            ...
    |-- meshes
        | -- bell_shape-300000.ply
        | -- bear_shape-300000.ply
             ...

训练BRDF色彩：

# estimate BRDF of the "bell" of the Glossy Synthetic dataset
python run_training.py --cfg configs/material/syn/bell.yaml

# estimate BRDF of the "bear" of the Glossy Real dataset
python run_training.py --cfg configs/material/real/bear.yaml

Intermediate results will be saved at data/train_vis. Models will be saved at data/model.

tensorboard —> train/loss 7k step左，100K step右

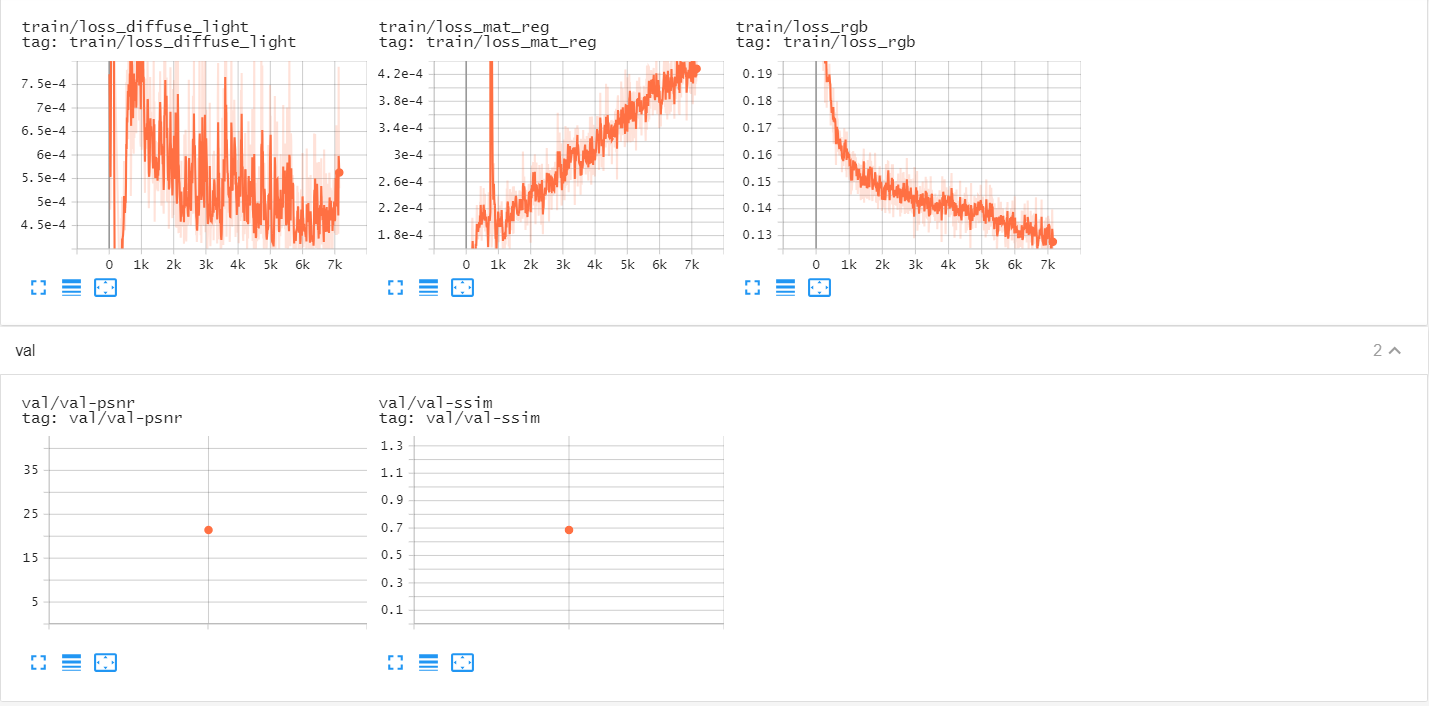
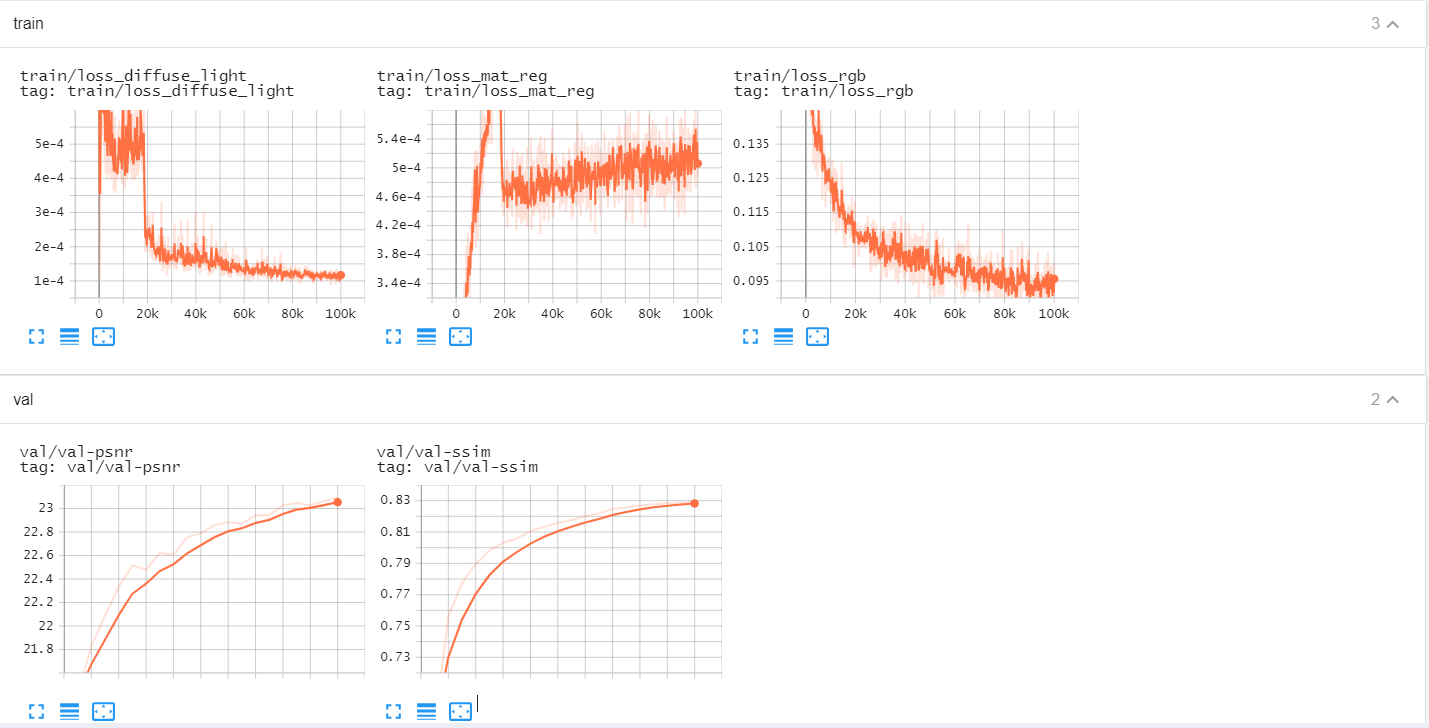
data/train_vis/bear_material-val/99999-index-0.jpg

Extract materials from the model

python extract_materials.py --cfg configs/material/syn/bell.yaml
python extract_materials.py --cfg configs/material/real/bear.yaml

The extracted materials will be saved at data/materials.

data/materials/bear_material-100000/

• albedo.npy
• metallic.npy
• roughness.npy

Relighting

使用blender进行relighting，渲染在hdr场景下的镜面反射物体

NeRO
|-- data
    |-- GlossyReal
        |-- bear 
            ...
    |-- GlossySynthetic
        |-- bell
            ...
    |-- meshes
        | -- bell_shape-300000.ply
        | -- bear_shape-300000.ply
             ...
    |-- materials
        | -- bell_material-100000
            | -- albedo.npy
            | -- metallic.npy
            | -- roughness.npy
        | -- bear_material-100000
            | -- albedo.npy
            | -- metallic.npy
            | -- roughness.npy
    |-- hdr
        | -- neon_photostudio_4k.exr

python relight.py --blender <path-to-your-blender> \
                  --name bell-neon \
                  --mesh data/meshes/bell_shape-300000.ply \
                  --material data/materials/bell_material-100000 \
                  --hdr data/hdr/neon_photostudio_4k.exr \
                  --trans
                  
python relight.py --blender <path-to-your-blender> \
                  --name bear-neon \
                  --mesh data/meshes/bear_shape-300000.ply \
                  --material data/materials/bear_material-100000 \
                  --hdr data/hdr/neon_photostudio_4k.exr

eg: 
python relight.py --blender F:\Blender\blender.exe --name bear-neon --mesh data/meshes/bear_shape-300000.ply --material data/materials/bear_material-100000 --hdr data/hdr/neon_photostudio_4k.exr

KeyError: 'bpy_prop_collection[key]: key "Principled BSDF" not found'
--> 需要将blender界面设置成英文

KeyError: ‘bpy_prop_collection[key]: key “Principled BSDF” not found’ · Issue #601 · carson-katri/dream-textures (github.com)

The relighting results will be saved at data/relight with the directory name of bell-neon or bear-neon. This command means that we use neon_photostudio_4k.exr to relight the object.

eg

syn/bell:

# stage1
python run_training.py --cfg configs/shape/syn/bell.yaml
python extract_mesh.py --cfg configs/shape/syn/bell.yaml
# stage2
python run_training.py --cfg configs/material/syn/bell.yaml
python extract_materials.py --cfg configs/material/syn/bell.yaml