| Title | NeuFace: Realistic 3D Neural Face Rendering from Multi-view Images |
|---|---|
| Author | Mingwu Zheng, Haiyu Zhang, Hongyu Yang, Di Huang |
| Conf/Jour | CVPR |
| Year | 2023 |
| Project | aejion/NeuFace: Official code for CVPR 2023 paper NeuFace: Realistic 3D Neural Face Rendering from Multi-view Images. (github.com) |
| Paper | NeuFace: Realistic 3D Neural Face Rendering from Multi-view Images (readpaper.com) |
贡献:
- BRDF+SDF+PBR新框架,端到端训练,重建出Face的外观和几何
- 简单而新的低秩先验,镜面反射部分的Material Integral. 表示为线性组合的BRDF基
Limitation
由于NeuFace主要侧重于复杂面部皮肤的反射建模,而没有明确解决更具挑战性的次表面散射问题,仅采用简化的阴影模型,因此本研究中获得的渲染结果的保真度可以进一步提高。
此外,NeuFace目前提供的是一个静态的3D人脸,而不是一个可驱动的人脸,虽然几何模型,即ImFace,是一个非线性变形模型,理论上支持可控的表情编辑,但需要更多的工作来提高性能。
Conclusion
本文提出了一种新的三维神经渲染模型,即:NeuFace,可以同时从多视图图像中捕获逼真的面部外观和几何形状。
为了处理复杂的面部皮肤反射率,我们将PBR与神经BRDFs结合起来,以获得更准确和更有物理意义的3D表示。
此外,为了促进底层brdf的优化,我们引入了一种split积分技术以及一种简单而新的低秩先验,这大大提高了恢复性能。
大量的实验证明了NeuFace在人脸绘制方面的优越性,以及对普通物体良好的泛化能力。
AIR
多视点图像的真实感人脸绘制对各种计算机视觉和图形学应用都有很大的帮助。然而,由于人脸具有复杂的空间变化的反射率特性和几何特征,在目前的研究中,如何真实有效地恢复三维人脸表征仍然是一个挑战。
本文提出了一种新的三维人脸绘制模型NeuFace,该模型通过神经绘制技术来学习精确且有物理意义的底层3D表示。它自然地将神经BRDFs合并到基于物理的渲染PBR中,以协作的方式捕获复杂的面部几何和外观线索。具体来说,我们引入了一个近似的BRDF积分和一个简单而新的低秩先验,有效地降低了模糊性,提高了面部BRDF的性能。大量的实验证明了NeuFace在人脸渲染方面的优势,以及对常见对象的良好泛化能力。
Introduction
Face Rendering问题
根据摄影测量学,在这个问题上的开创性研究通常利用复杂的主动照明设置,例如:LightStage[9]等,从个人的多张照片中构建3D人脸模型,其中准确的形状属性和高质量的漫反射和镜面反射属性通常被认为是其成功的前提。需要一个精心设计的工作流程,通常涉及相机校准、动态数据采集、多视角立体、材料估计和纹理参数化等一系列阶段[44]。虽然最终可以获得令人信服的3D人脸模型,但这种输出在很大程度上取决于工程师和美工的专业知识,因为多步骤的过程不可避免地会带来不同的优化目标。
最近,3D神经渲染提供了一种端到端替代方案,在从现实世界图像中恢复场景属性方面表现出了很好的性能,例如视图相关的亮度[27,29,37,39,49]和几何形状[34,50,51,56,57]。这主要归功于可学习的3D表示和可微分的图像形成过程的解开,摆脱了繁琐的摄影测量管道。然而,像经典的函数拟合一样,反向渲染从根本上是不受约束的,这可能会导致底层3D表示的条件拟合不良,特别是对于复杂的情况,例如,具有视图依赖高光的非兰伯曲面。随着计算机图形学与学习技术相结合的趋势,一些尝试利用物理动机的归纳偏差,并提出了基于物理的渲染(PBR)[15,32,49,58],其中双向反射分布函数(brdf)被广泛采用。通过明确地模拟环境光与场景的相互作用,它们促进了网络优化并提供了可观的收益。不幸的是,被利用的物理先验要么是启发式的,要么是分析性的[8,21,46],仅限于一小部分现实世界的材料,例如金属,无法描述人脸。
对于逼真的人脸渲染,最根本的问题在于准确建模多层面部皮肤的光学特性[22]。特别是,分布不均的细尺度油层和表皮不规则地反射入射光,导致复杂的视依赖和空间变化的高光。这种特征和面部表面的低纹理性质强烈地放大了形状-外观的模糊性。此外,真皮层和其他皮肤层之间的表皮下散射也使这一问题更加复杂。
在本文中,我们遵循了PBR范式在学习3D表示方面的潜力,并迈出了逼真的3D神经面部绘制的第一步,主要针对复杂的皮肤反射建模。我们的方法,即NeuFace,能够从多视图图像中恢复忠实的面部反射率和几何形状。具体来说,我们建立了一个PBR框架来学习神经BRDFs来描述面部皮肤,它模拟了物理正确的光传输,具有更高的表示能力。通过使用一种基于可微分符号距离函数(SDF)的表示方法,即ImFace[63]作为形状先验,可以在反渲染中同步优化面部外观和几何场。
与分析型BRDFs相比,神经型BRDFs可以更丰富地表征面部皮肤等复杂材料。尽管有这种优势,但这种表示对训练期间的计算成本和数据需求提出了挑战。为了解决这些困难,实时渲染技术[1]被用来分离神经 BRDFs 的半球积分,其中物质积分和光积分被单独学习,绕过了数值解法所需的大量 Monte-Carlo 采样阶段[35]。此外,在空间变化的面部BRDFs中引入了低秩先验,极大地限制了解空间,从而减少了对大规模训练观测的需求。这些模型设计确实使NeuFace能够像在真实的3D空间中一样,准确而稳定地描述光与面部表面的相互作用。图1显示了一个示例。

本研究的主要贡献包括:
1)一个具有自然结合的PBR和神经BRDF表示的新框架,协同捕获复杂面部皮肤的面部几何和外观属性。
2)一种新的、简单的低秩先验,极大地促进了神经brdf的学习,提高了外观恢复性能。
3)令人印象深刻的人脸渲染结果仅来自多视图图像,适用于各种应用,如重照明,以及对常见物体的良好泛化能力。
Related Work
我们将讨论具体限于静态面部几何和外观捕获以及3D神经渲染。请参考[10,22,45]进行更深入的讨论。
Face Capturing
它的目标是在任意光照条件下渲染一个逼真的3D人脸。
- 现有的方法通常利用摄影测量技术来估计面部几何形状和外观,需要大量的人工工作。在这种情况下,它们通常分解问题,其中面部几何形状是通过复杂的多视图立体过程预先捕获的[3,4]。然而,由于光与皮肤之间复杂的相互作用,具有反射率的面部外观仍然难以获得。
- 最初的尝试[9,17,53]通过密集地捕获每像素的面部反射率来解决这一挑战,这需要大量的数据采集和专门的设备。随后,梯度[12,20,26]或偏光[12,13,26,40]被探索以减少记忆成本,其中大部分精力都花在brdf的良好条件拟合上。
- 与上述研究相比,我们的解决方案是真正的端到端,只在单一的、未知的照明条件下观察面部皮肤,没有繁琐的捕捉设置。
3D Neural Rendering
- 该领域的最新进展,如NeRF[30],已经彻底改变了多视图重建的范式。使用可学习的体积表示(例如,神经场[30,57],网格[11]和混合[31])和解析可微前向映射,仅从2D图像就可以直接推断出场景属性。虽然在新的视图合成[27,29,37,39,49]或几何重建[34,50,51,56,57]方面取得了令人印象深刻的成果,但研究仍然存在2D-3D模糊性,导致难以同时建立真实的外观和精确的几何形状[59]。由于面部皮肤的反射特性比较复杂,这个问题更加突出。
- Ref-NeRF[49]向精确表面法线和光滑外观的目标迈进了一步,这是通过用反射方向重新参数化经典NeRF中的辐射来实现的。它验证了物理定律在模糊中的意义。[15,23,32,43,58]进一步采用PBR管道,同时提供更高的质量和支持重照明。然而,使用或假设的简化材料模型无法处理皮肤等复杂材料。
- NeRFactor等[25,61,62]从测量数据训练神经材料模型。但是获取这样的数据对于活的生物组织来说是不切实际的
相比之下,我们的方法直接构建神经皮肤brdf,重建精确的几何线索,而不需要任何外部数据。
Preliminaries
我们采用PBR[19]来显式预测复杂的skin reflectances,其中表面位置x处的辐射度$L_{o}$沿方向$\omega_{o}$可以表示为: $L_o(x,\omega_o)=\int_{S^2}L_i(\omega_i)f(x,\omega_i,\omega_o)(\omega_i\cdot\mathbf{n})^+\mathrm{d}\omega_i,$ Eq.1
其中,$L_{o}$的计算方法是对从$\omega_{i}$方向入射亮度$L_{i}$、皮肤BRDF f和表面法向$\mathbf{n}$与$\omega_{i}$球面$S^2$之间的半余弦函数$(\omega_i\cdot\mathbf{n})^+$的乘积进行积分。假设无阴影的单弹直接照明,因此$L_{i}$与x无关。此外,由于假设像素级的次表面散射,$L_{o}$只考虑单个小区域。
球面谐波(SH)[6]和球面高斯(SG)[58]通常被用作入射照明的有效表示。本研究选择SH是因为它的完备性和紧凑性。更重要的是,它可以隐式地促进低阶的镜面分离[47]。因此,未知$L_{i}$可以用前十阶的球形基函数$Y_{\ell m}$乘以相应的可学习系数$c_{\ell m}$来近似:$L_i(\omega_i)\approx\sum_{\ell=0}^{10}\sum_{m=-\ell}^{\ell}c_{\ell m}Y_{\ell m}(\omega_i),$ Eq.2
f被建模为两个组件,类似于现有技术
$f\left(x,\omega_i,\omega_o\right)=\frac{\mathbf{a}(x)}\pi+\varrho f_\mathrm{s}\left(x,\omega_i,\omega_o\right),$ Eq.3
其中左项是漫反射分量(Lambertian),仅由反照率a(x)决定,剩余项主要负责光滑反射,由$f_\mathrm{s}\left(x,\omega_i,\omega_o\right)$表示,其比例因子$\varrho$表示镜面强度。因此,渲染方程(Eq.(1))可分为两项:
Eq.4:
$L_o(x,\omega_o)=\underbrace{\frac{\mathbf{a}(x)}{\pi}\int_{S^{2}}L_i(\omega_i)(\omega_i\cdot\mathbf{n})^{+}\mathrm{d}\omega_i}_{\text{diffuse term }L_\mathrm{d}} +\underbrace{\varrho\int_{S^2}L_i(\omega_i)f_\mathrm{s}(x,\omega_i,\omega_o)(\omega_i\cdot\mathbf{n})^+\mathrm{d}\omega_i}_{residual (specular) term L_{8}}$
Method
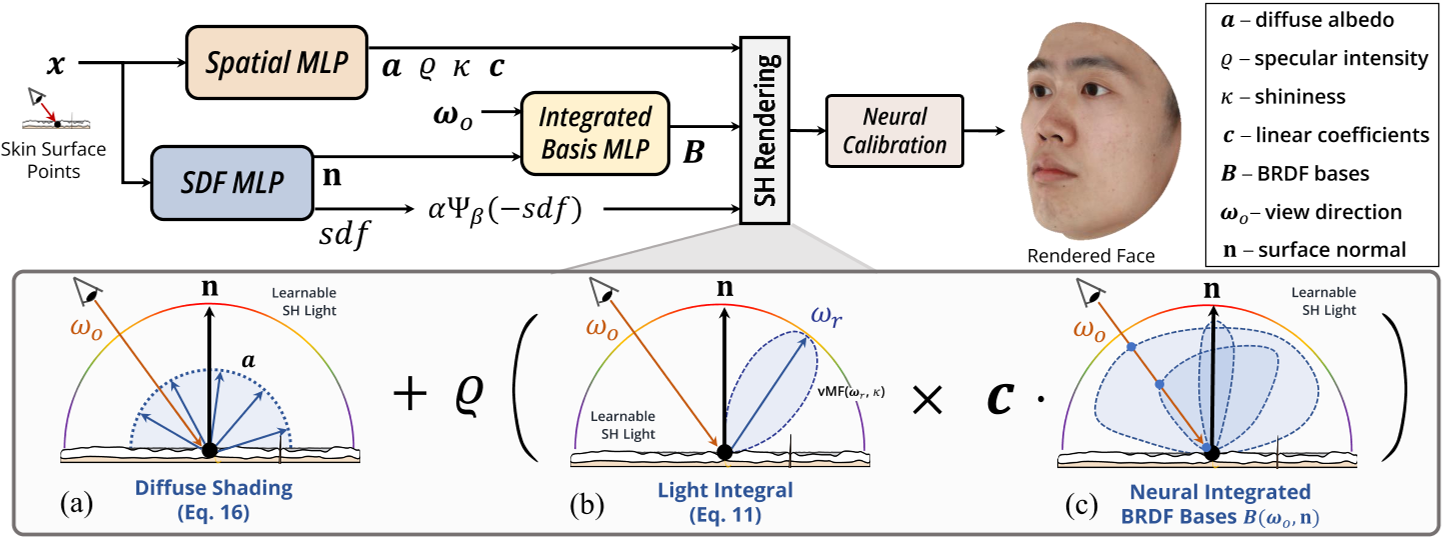
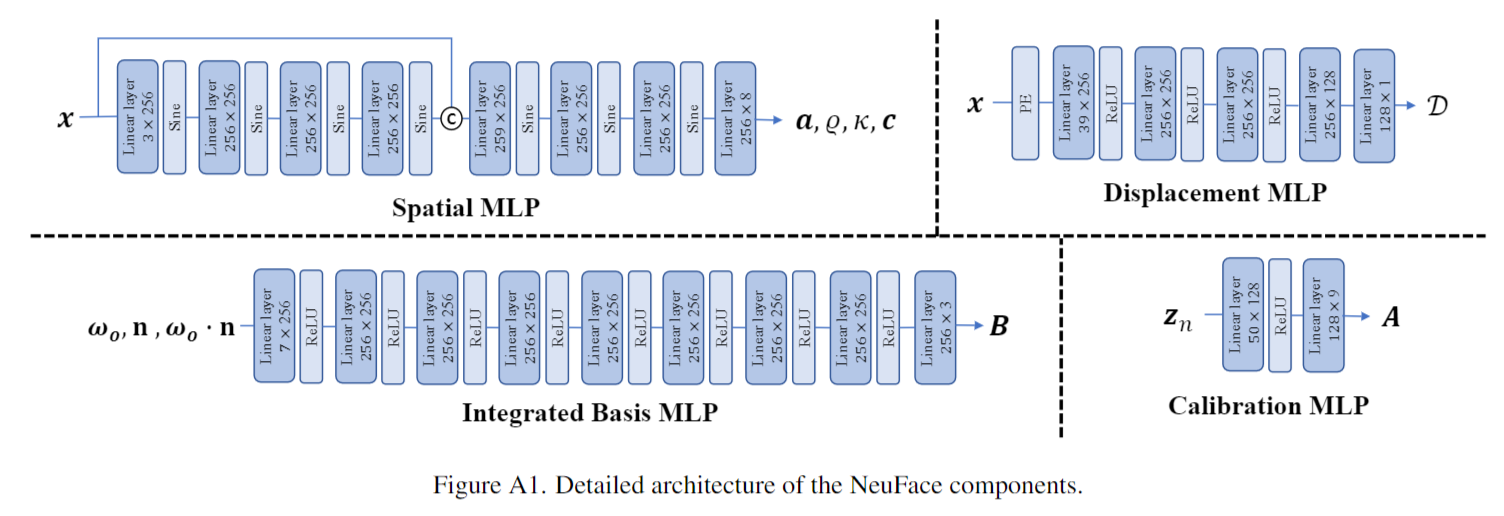
我们将神经brdf整合到PBR中,以协同学习复杂的外观属性(即漫射反照率和镜面反照率)和复杂的几何属性。提出的NeuFace从多视图图像中进行3D人脸捕获,只需要额外的相机姿势。如图2所示,它利用Spatial MLP和Integrated Basis MLP来学习皮肤BRDFs,并通过将其明确分解为漫反射反照率、光积分和BRDFs积分来模拟物理正确的光传输。面部外观建模可以用Eq.(4)表示,我们努力解决学习过程中计算成本高和数据需求大带来的挑战。为了获得更准确的估计,NeuFace进一步利用基于sdf的表示,即imface[63],作为前向映射的面部几何形状。通过端到端的逆渲染,将人脸外观和几何场联合恢复。

Specular Modeling
对于带有BRDF $f_\mathbf{s}(x,\omega_i,\omega_o),$的镜面项$L_{\mathrm{s}}$,由于$\omega_{o}$的视域依赖特性,难以求解。在先前处理非面部神经渲染的研究中,分析BRDFs,例如microfacet模型[32,42,58],已被用于近似积分。然而,这些显式模型只能恢复一小部分材料,而不包括具有相当独特属性的面部皮肤[33]。为了获得更强的表示能力,NeRFactor[61]采用了从真实世界捕获的MERL数据库[28]中学习到的数据驱动BRDFs,但面部皮肤等具有空间变化BRDFs的活组织在体内[16]极难测量。此外,在NeRFactor中必须执行大量蒙特卡罗采样来求解渲染方程,这在我们的情况下是不实用的,因为面部几何形状最初是未知的。
在这项研究中,我们提出了一种不需要外部数据和数值积分的方法来渲染复杂的面部高光。特别地,受到实时渲染[1]中的分裂积分近似的启发,对镜面进行了分解,其中$L_{\mathrm{s}}$可以近似为: $L_{\mathrm{s}}\approx\varrho\int_{\mathrm{s}^{2}}f_{\mathrm{s}}\left(x,\omega_{i},\omega_{o}\right)(\omega_{i}\cdotp\mathrm{n})^{+}\mathrm{d}\omega_{i}\int_{\mathrm{s}^{2}}D(h)L_{i}\left(\omega_{i}\right)\mathrm{d}\omega_{i}$ Eq.5
其中D(h)是一个分布函数,表示光在半向量$h=\frac{\omega_i+\omega_o}{|\omega_i+\omega_o|_2}$处的反射。整个方程两侧分别是材料和光的积分项,它们在后面分别求解。
Material Integral.
Eq.(5)中的第一个分裂积分项仅与材料属性有关,在我们的方法中,材料属性由可学习网络参数化,以获得更高的面部皮肤表示能力。考虑到二维观测只能约束积分值,而不是像[61,62]那样建模$f_{\mathrm{s}}(\tilde{x,\omega_{i}},\omega_{o})$,我们直接将整个积分表示为更平滑的函数F: $\int_{\mathrm{s}^{2}}f_{\mathrm{s}}\left(x,\omega_{i},\omega_{o}\right)\left(\omega_{i}\cdot\mathbf{n}\right)^{+}\mathrm{d}\omega_{i}=F(x,\omega_{o},\mathbf{n}).$ Eq.6
需要注意的是,对于这样一个空间变化的9变量函数,使用MLP实现鲁棒拟合需要大量的真实样本,这在实践中是不可用的。基于之前对人脸外观测量的研究[13,53],我们提出了一个关键假设,即个体的所有面部表面位置都具有相似的镜面结构,因此空间变化的特性可以由少数(低秩)可学习BRDFs的不同线性组合表示:
$f_\mathrm{s}\left(x,\omega_i,\omega_o\right)\approx\sum_{j=1}^{k}c_j(x)b_j(\omega_i,\omega_o),$ Eq.7
其中$\{b_j(\omega_i,\omega_o)\}_{j=1}^k$表示k个全局与空间无关的BRDF基,$\mathbf{c}(x)=[c_1(x),c_2(x),…,c_k(x)]^T$表示每个表面位置x对应的线性系数。
因此,材料积分可表示为:
$\int_{\mathrm{s}^2}f_\mathrm{s}\left(x,\omega_i,\omega_o\right)(\omega_i\cdot\mathbf{n})^+\mathrm{d}\omega_i=\mathbf{c}(x)\cdot\mathbf{B}(\omega_o,\mathbf{n}),$ Eq.8
式中$\mathbf{B}(\omega_o,\mathbf{n})=[B_1,B_2,…,B_k]^T$表示k积分BRDF基$b_{j}$乘以半余弦函数$(\omega_{i}\cdot\mathbf{n})^{+}$:
$B_j(\omega_o,\mathbf{n})=\int_{\text{s}^2}b_j\left(\omega_i,\omega_o\right)(\omega_i\cdot\mathbf{n})^+\mathrm{d}\omega_i,j=1,2,…,k.$ Eq.9
我们利用一个MLP,即Integrated Basis MLP,来拟合$\mathbf{B}(\omega_o,\mathbf{n})$。$\omega_{o}\cdot\mathbf{n}$也被输入其中,以考虑菲涅耳效应。同时,以x为输入的Spatial MLP预测系数向量$\mathbf{c}(x)$。请注意,面部皮肤是介电的,不能对高光着色,因此我们使用单个通道$B_{j}$来表示单色面部brdf 。
如图 2 (c) 所示,低秩先验全局限制了所有面部镜面的解空间,而不强制任何空间平滑性[55]或采样位置聚类[32]。有了这样的先验,材料积分项就更容易拟合和插值,只需适量的训练数据就能产生令人印象深刻的结果。

Light Integral.
对于光滑表面,反射能量主要集中在反射方向附近,用$\omega_{r}$表示,如图2 (b)所示。因此,我们将$D(h)$建模为三维归一化球面高斯分布(vMF),以$\omega_{r}$为中心,浓度参数κ表示亮度: $D(h)\approx\mathrm{vMF}(\omega_i;\omega_r,\kappa),$
κ是由Spatial MLP预测的,较大的值表明指向$\omega_{r}$的BRDF波瓣更尖锐,使面部皮肤看起来更有光泽。正如我们补充材料中的证明所示,方程(5)中描述镜面光输运的第二次分裂积分可以近似为:
$\int_{\mathrm{s}^2}D(h)L_i\left(\omega_i\right)\mathrm{d}\omega_i\approx\sum_{\ell=0}\sum_{m=-\ell}^{\ell}e^{-\frac{\ell(\ell+1)}{2\kappa}}c_{\ell m}Y_{\ell m}(\omega_r).$ Eq.11
然后,神经brdf (Eq.(4))中的整个镜面项可以有效地微分计算为:
$L_\mathrm{s}\approx\varrho\left(\mathbf{c}(x)\cdot\mathbf{B}(\omega_o,\mathbf{n})\right)\sum_{\ell=0}\sum_{m=-\ell}^{\ell}e^{-\frac{\ell(\ell+1)}{2\kappa}}c_{\ell m}Y_{\ell m}(\omega_r).$ Eq.12
Diffuse Modeling
由式(2)可知,表面位置x处的漫射亮度$L_{\mathrm{d}}$可改写为:
$L_{\mathrm{d}}(x)=\frac{\mathbf{a}(x)}{\pi}\sum_{\ell=0}\sum_{m=-\ell}^{\ell}c_{\ell m}\int_{\mathrm{s}^{2}}Y_{\ell m}\left(\omega_{i}\right)\left(\omega_{i}\cdot\mathbf{n}\right)^{+}\mathrm{d}\omega_{i}.$Eq.13
根据Funk-Hecke定理[2],$(\omega_{i}\cdot\mathbf{n})^{+}$与球次谐波$Y_{\ell m}$的卷积可解析计算为:
$\int_{\mathrm{s}^{2}}Y_{\ell m}\left(\omega_{i}\right)\left(\omega_{i}\cdot\mathrm{n}\right)^{+}\mathrm{d}\omega_{i}\approx\Lambda_{\ell m}Y_{\ell m}(\mathrm{n}),$ Eq.14
$\Lambda_{\ell m}=\begin{cases}\frac{2\pi}{3},&\mathrm{if~\ell=1,}\\\frac{(-1)^{\ell/2+1}\pi}{2^{\ell-1}(\ell-1)(\ell+2)}\binom{\ell}{\ell/2},&\mathrm{if~\ell~is~even},\\0,&\mathrm{if~\ell~is~odd},\end{cases}$ Eq.15
详见[2]。在NeuFace中,漫射反照率a(x)由Spatial MLP建模。对于可学习的SH照明系数$c_{lm}$,漫射项可直接计算为: $L_{\mathrm{d}}(x)\approx\frac{\mathbf{a}(x)}{\pi}\sum_{\ell=0}\sum_{m=-\ell}^{\ell}\mathbf{\Lambda}_{\ell m}c_{\ell m}Y_{\ell m}\left(\mathbf{n}\right).$ Eq.16
综上所述,NeuFace的外观分量由一个Spatial MLP: $\begin{aligned}x\mapsto(\varrho,\mathbf{c},\kappa,\mathbf{a})\end{aligned}$,一个Integrated Basis MLP:$(\omega_o,\mathbf{n},\omega_o\cdot\mathbf{n})\mapsto\mathbf{B}$,以及可学习的环境光系数$c_{\ell m}.$组成。最后可以通过Eq.(12)和Eq.(16)估算出Radiance $L_{o}$。
Geometry Modeling
为了实现端到端训练,一个可微的几何表示是必不可少的。与大多数神经渲染实践类似[50,56 - 58],神经SDF可用于隐式定义面部几何形状。在这里,我们利用ImFace[63]作为直接的面部SDF,以便于采样和训练。为了捕获先验分布之外的几何形状,我们对ImFace I: $x\mapsto\mathrm{SDF}$进行微调,并引入神经位移场$\mathcal{D}(x)$来纠正最终结果:$\mathrm{SDF}(x)=\mathcal{I}(x)+\mathcal{D}(x).$ Eq.17
根据SDF的性质,可以通过自梯度提取表面法向n: $\mathbf{n}=\nabla\text{SDF}(x).$。
Sampling and Rendering
为了处理多层面部皮肤,我们像VolSDF[56]一样对亮度值进行体积渲染。对于从相机位置$\mathbf{o}\in\mathbb{R}^3$向$\omega_{o}$方向发射的射线$x(t)$,定义为$x(t)=\mathbf{o}+t\omega_{o},t>0,$,密度函数定义为$\sigma(t)=\beta^{-1}\Psi_{\beta}(-\mathrm{SDF}(x(t))).$。$\Psi_{\beta}$为零均值拉普拉斯分布的累积分布函数和学习到的尺度参数β。因此,每条射线的综合辐射度由以下公式计算:
$\mathbf{I}(\mathbf{o},\omega_o)=\int_{t_a}^{t_b}L_o(x(t),\omega_o)\sigma(t)T(t)\mathrm{d}t,$ Eq.18
其中$T(t)=\exp(-\int_{0}^{t}\sigma(s)\mathrm{d}s)$为透明度。
为了加速渲染,我们不像[56]那样沿着射线密集采样点,而是首先进行积极的球体追踪[24],快速找到表面附近的位置$t_{0}$(阈值为0.05mm),然后从$t\in[t_a,t_b]$均匀采样32个点,其中$\begin{aligned}t_a=t_0-0.5mm\end{aligned}$,$t_{b}=t_{0}+0.5mm.$。如图3所示,对于未击中表面的光线,我们从ImFace[63]中稀疏采样由先前几何定义的球体Ω内的点,并计算累积,绕过需要大量采样的掩膜损失[57]。通过结合体和表面渲染,它在渲染质量、几何精度和采样效率之间取得了很好的平衡。
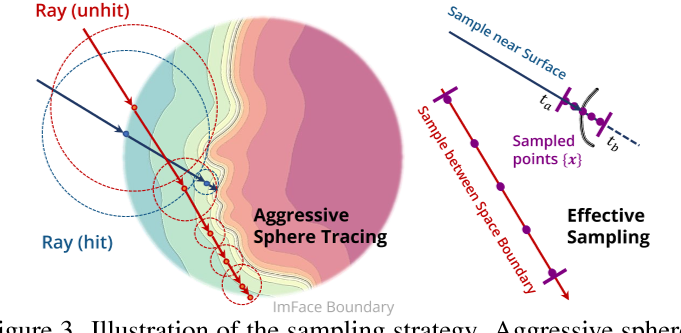
抽样策略的说明。采用侵略性球体跟踪来加速体绘制的采样过程。对于未击中表面的光线,使用ImFace的几何先验定义的球体来约束采样空间。
Neural Photometric Calibration
为了自动校准相机之间不一致的色彩响应和白平衡,我们将每个图像的线性映射矩阵$\mathbf{A}_n\in \mathbb{R}^{3\times3}$应用于渲染的亮度值: $\mathbf{I}_n=\mathbf{A}_n\mathbf{I},$ Eq.19
其中$\mathbf{A}_{n}$由基于可学习的每幅图像嵌入的轻量级MLP预测。
Loss Functions
NeuFace 通过复合批评器进行训练,以学习准确的外观和几何属性: $\mathcal{L}=\mathcal{L}_{RGB}+\mathcal{L}_{white}+\mathcal{L}_{spec}+\mathcal{L}_{geo}.$ Eq.20
设$P_{n}$为第n张多视图图像$\bar{\mathbf{I}}_n.$的像素。$\mathcal{L}$的每一项描述如下,其中λ表示权衡超参数。
- Reconstruction Loss.它用于监督渲染的2D人脸是否接近真实观测值:
- $\mathcal{L}_{RGB}=\lambda_{1}\sum_{n}\sum_{\omega_{o}\in P_{n}}|\mathbf{I}_{n}-\bar{\mathbf{I}}_{n}|.$ Eq.21
- Light Regularization.我们假设捕获的环境光接近白色,通过以下方式实现:
- $\mathcal{L}_{white}=\lambda_{2}\sum_{n}\sum_{\omega_{o}\in P_{n}}|L_{i}-\bar{L}_{i}|,$ Eq.22
- 其中,$\bar{L}_i$是通过平均RGB通道来计算的。
- Facial Specular Regularization.只有一小部分入射光在表面上(大约6%[48])直接反射,因此我们通过以下方式惩罚镜面能量:
- $\mathcal{L}_{spec}=\lambda_3\sum_n\sum_{\omega_o\in P_n}L_s.$ Eq.23
- Geometry Losses. Following ImFace,利用嵌入正则化、Eikonal正则化和一种新的残差约束进行精确几何建模:
- $\mathcal{L}_{geo}=\lambda_{4}|\mathbf{z}|^{2}+\lambda_{5}\sum_{x\in\Omega}||\nabla\mathrm{SDF}(x)|-1|+\lambda_{6}\sum_{x\in\Omega}|\mathcal{D}(x)|,$ Eq.24
- 其中z代表ImFace的嵌入
Experiments
Dataset: FaceScape
Comparison
- NeRF, Ref-NeRF
- Volume Rendering of Neural Implicit Surfaces
- Extracting Triangular 3D Models, Materials, and Lighting From Images
- PhySG
- DIFFREC
metrics: PSNR、SSIM[52]和LPIPS[60]、Chamfer distance
Ablation Study
- On Shading Model.
- On Neural Integrated Basis.
Extension to Common Objects
- DTU