| Title | Ref-NeuS: Ambiguity-Reduced Neural Implicit Surface Learning for Multi-View Reconstruction with Reflection |
|---|---|
| Author | Wenhang Ge1 Tao Hu 2 Haoyu Zhao 1 Shu Liu 3 Ying-Cong Chen1,∗ |
| Conf/Jour | ICCV Oral |
| Year | 2023 |
| Project | Ref-NeuS (g3956.github.io) |
| Paper | Ref-NeuS: Ambiguity-Reduced Neural Implicit Surface Learning for Multi-View Reconstruction with Reflection (readpaper.com) |
- Anomaly Detection for Reflection Score + Visibility Identification for Reflection Score
- Reflection Direction Dependent Radiance反射感知的光度损失
Limitation and Conclusion
Limitation:尽管我们的方法在带反射的多视图重建中显示出良好的效果,但仍然存在一些局限性。
- 首先,估计反射分数不可避免地增加了计算成本。
- 其次,简单地用反射方向取代辐射网络的依赖关系,而不管物体的材质如何,在某些情况下都会导致伪影。我们在补充材料中给出了这样一个人工制品的例子。
Conclusion:本文研究了具有反射表面的物体的多视点重建问题,这是一个重要但尚未得到充分研究的问题。反射引起的模糊会严重破坏多视图的一致性,但我们提出的Ref-NeuS方法通过引入反射感知的光度损失来解决这个问题,其中反射像素的重要性使用高斯分布模型衰减。此外,我们的方法采用了反射方向相关的辐射,这进一步改善了几何形状,具有更好的辐射场,包括几何形状和表面法线。
AIR
神经隐式表面学习在多视图三维重建中取得了重大进展,其中物体由MLP表示,这些感知器提供连续的隐式表面表示和与视图相关的亮度。然而,目前的方法往往不能准确地重建反射表面,导致严重的模糊性。为了克服这个问题,我们提出了Ref-NeuS,旨在通过降低反射表面的重要性来减少模糊性。具体来说,我们利用异常检测器在多视图context的指导下估计显式反射分数来定位反射表面。之后,我们设计了一个反射感知的光度损失,通过将渲染颜色建模为高斯分布,以反射分数表示方差variance,自适应地减少模糊。我们表明,与反射方向相关的辐射一起,我们的模型在反射表面上实现了高质量的表面重建,并且在很大程度上优于最先进的技术。此外,我们的模型在一般表面上也具有可比性。
Introduction
三维重建是计算机视觉中的一项重要任务,是计算机辅助设计[20,8]、计算机动画[33,23]、虚拟现实[40]等多个领域的基础。在各种三维重建技术中,基于图像的三维重建技术尤其具有挑战性,其目的是从构成的二维图像中恢复三维结构。传统的多视角立体(MVS)方法[11,39,51]通常需要一个多步骤的管道,并带有监督,这可能很麻烦。最近,神经隐式表面学习[45,52,31]因其能够以支持端到端和无监督训练的整洁公式实现卓越的重建质量而受到越来越多的关注。然而,如图1所示,现有的方法往往在反射表面(如镜面高光)产生错误的结果。由于这些方法推断的几何信息具有多视图一致性,因此由于反射表面上几何网络的表面预测不明确而影响了多视图一致性。因此,在反射不可避免的情况下,它们的实用性受到限制。
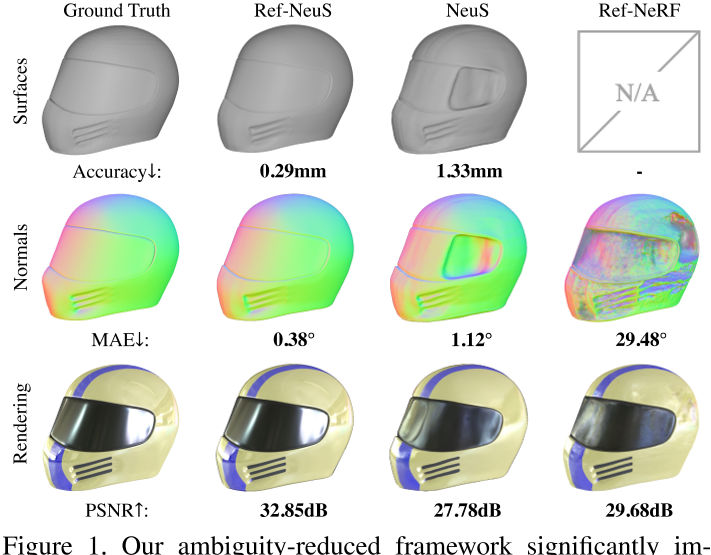
最近的一些研究[3,42,55,57,43]研究了神经辐射场的反射建模。这些方法通常将对象的外观分解为几个物理组件,从而允许显式地表示反射。通过消除反射分量的影响,可以更好地估计3D几何形状。然而,物理分解可能是高度不适定的[14],不准确的分解会严重限制性能。例如,如图1所示,Ref-NeRF[43]中预测的norm不够准确,从而导致性能次优。
在本文中,我们提出了一个简单而有效的解决方案,不依赖于具有挑战性的物理分解。
相反,我们建议通过引入反射感知光度损失来减少模糊性,该光度损失可根据反射分数自适应地降低拟合反射表面的权重。通过这样做,我们避免了破坏性的多视图一致性。此外,受Ref-NeRF[43]和NeuralWarp[7]的启发,我们表明我们可以通过用反射方向代替辐射依赖关系来进一步改进几何形状,以获得更准确的辐射场。如图1所示,我们的模型在预测表面几何形状(顶部行)和表面法线(中间行)方面优于其他竞争方法。此外,通过估算更精确的表面法线来确定反射方向的准确性,我们还可以实现有希望的渲染真实感,作为一个额外的benefit(底部行)。
虽然上面讨论的想法很简单,但设计反射感知的光度损失是非常重要的。一种直接的方法是遵循NeRF-W[27],其中vanilla光度损失被扩展到贝叶斯学习框架[19]。它将辐射表示为高斯分布,学习到的不确定性表示方差,期望不确定性可以在野外定位图像的瞬态分量,消除其对静态分量学习的影响。然而,这种方法并不适用于反射场景,因为它学习了只考虑单一光线信息而忽略多视图context的隐含不确定性。
为了解决这个问题,我们建议定义一个明确的反射分数,该分数利用参考同一表面点的多视图图像的像素颜色获得的多视图context。首先,我们确定给定一个表面点的所有源视图的可见性。接下来,我们将点投影到可见图像中以获得像素颜色。在此基础上,我们使用异常检测器来估计反射分数,该分数作为方差。通过最小化颜色高斯分布的负对数似然,较大的方差会减弱其重要性。我们进一步证明,通过使用反射方向相关的辐射,我们的模型在具有更好的辐射场的多视图重建中取得了令人满意的结果。
贡献:
- 据我们所知,我们提出了第一个用于重建具有反射表面的物体的神经隐式表面学习框架。
- 我们提出了一种简单而有效的方法,使神经隐式表面学习处理反射表面。我们的方法可以产生高质量的表面几何形状和表面法线。
- 在多个数据集上进行的大量实验表明,所提出的框架在反射表面上的性能明显优于最先进的方法。
Related Works
Multi-View Stereo for 3D Reconstruction
多视图立体(MVS)是一种旨在从多视图图像中重建细粒度场景几何结构的技术。传统的MVS方法可以根据输出场景的表示分为四类: 基于体积的方法[6,41]、基于网格的方法[10]、基于点云的方法[11,24]和基于深度图的方法[4,12,38,39,47]。其中,基于深度图的方法最为灵活,利用参考图像和相邻图像的光度一致性估计每个视图的深度图[11],然后将所有深度图融合成密集的点云。然后采用表面重建方法[6,18,22],如筛选泊松表面重建[18],从点云重建表面。
然而,基于学习的MVS方法在某些情况下仍然可能产生令人不满意的结果,例如镜面反射的表面,低纹理的区域和非兰伯特区域。在这些情况下,不能保证多视图图像的光度一致性,这可能导致重建结果中出现严重的伪影和缺失部分。
Neural Implicit Surface for 3D Reconstruction
近年来,人们提出了基于学习的隐式表面表示方法。在这些表示中,神经网络将三维空间中的连续点映射到占用场[29,36]或有符号距离函数(SDF)[34]。这些方法执行多视图重建,并根据每个点的占用值或SDF进行额外的监督。然而,对这些方法的监督并不总是适用于only多视图2D图像,这限制了它们的可扩展性。
在NeRF[30]中引入的体积方法将经典的体绘制[16]与用于新型视图合成的隐式函数相结合,引起了人们对使用神经隐式表面表示和体绘制进行三维重建的大量关注[31,52,45]。与NeRF不同,NeRF旨在呈现新颖的视图图像,同时保持几何形状不受约束,这些方法以更明确的方式定义表面,因此更适合表面提取。UNISURF[31]使用占用域[29],而IDR[53]、VolSDF[52]和NeuS[45]使用SDF域[34]作为隐式表面表示。尽管这些方法在三维重建方面表现良好,但它们无法恢复具有反射的物体的正确几何形状,导致表面优化模糊不清。我们的方法建立在NeuS[45]的基础上,但我们相信它可以适应任何体积神经隐式框架
Modeling for Object with Reflection
我们讨论了具有反射的物体的渲染和重建。最近的作品[3,42,55,57,43]研究了通过将场景分解为形状、反射率和照明来渲染视图依赖的反射外观,以实现新的视图合成和重照明。然而,恢复的网格没有明确验证,几何形状往往不令人满意。另一方面,重建旨在恢复显式几何,由于固有的挑战,这一领域仍未得到充分探索。例如,PM-PMVS[5]将重建任务定义为曲面几何和反射率的联合能量最小化,而nLMVS-Net[49]将MVS定义为端到端可学习网络,利用表面法线作为与视图无关的表面特征进行成本体积构建和过滤。然而,这些方法都没有将神经隐式曲面与体绘制相结合进行重建。
Warping-based Consistency Learning
基于翘曲的一致性学习广泛应用于MVS[44,48,47,54]和神经隐式表面学习[7,9]中,通过利用可微翘曲操作的图像间对应关系进行三维重建。通常,基于mvs的管道中的一致性学习是在CNN特征级进行的。例如,MVSDF[54]将预测的表面点扭曲到相邻视图,并强制逐像素特征一致性,而ACMM[47]将粗预测深度扭曲,形成多视图聚合的几何一致性成本,以细化更精细的尺度。另一方面,基于神经隐式表面的管道中的一致性学习通常在图像级别进行。NeuralWarp[7]将采样点沿射线弯曲到源图像,获得其RGB值,并与辐度网络联合优化,Geo-Neus[9]将以预测表面点为中心的灰度斑块弯曲到邻近图像,以保证多视图几何一致性。然而,它们忽略了与视图相关的辐射,并且当由于反射而导致多视图一致性不合理时受到限制,这可能导致在最小化贴片相似性时产生伪影,而不管反射如何。此外,可见性识别处理得不好,两者都依赖于繁琐的预处理来确定源图像。Alternatively,我们利用不一致性来减少高保真重建的模糊性。
Approach
给定具有反射表面的物体的N幅校准多视图图像$\mathcal{X}=\left\{\mathbf{I}_{i}\right\}_{i=1}^{N}$,我们的目标是通过神经隐式表面学习来重建表面。
- 第3.1节介绍了我们用于重建的基线Neus。
- 第3.2节介绍了反射感知的光度损失。它通过将渲染颜色表述为高斯分布并考虑多视图context的显式方差估计来减少反射的影响。
- 第3.3节讨论了我们如何识别源视图的可见性以获得无偏反射分数。
- 第3.4节显示,与反射方向相关的辐射一起,我们的模型通过更好的辐射场获得更好的几何形状。
- 最后,第3.5节给出了完整的优化。图2概述了我们的方法。
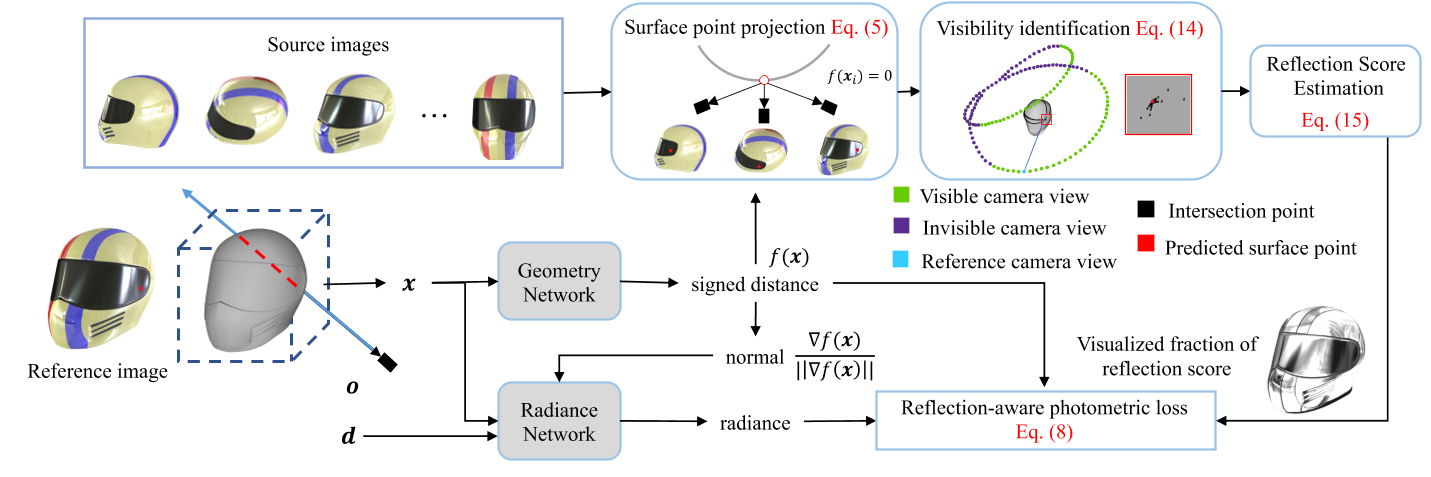
Volume Rendering with Implicit Surface
体绘制[16]在NeRF[30]中被用于新视图合成。这个想法是用神经网络来表示3D场景的连续属性(如密度和亮度)。α合成[28]沿着射线r聚集这些属性,通过以下方式近似像素RGB值:
$\hat{\mathbf{C}}(\mathbf{r})=\sum_{i=1}^{P}T_{i}\alpha_{i}\mathbf{c}_{i},$ Eq.1
$T_i=\exp\left(-\sum_{j=1}^{i-1}\alpha_j\delta_j\right)$, $\alpha_i=1-\exp{(-\sigma_i\delta_i)}$分别表示采样点的透光率和alpha值
$δ_{i}$是相邻采样点之间的距离。P是沿一条射线采样点的个数。在位置x = (x, y, z)和视场方向$d = (θ, φ)$的条件下,神经网络预测属性$σ_{i}$和$c_{i}$。NeRF的训练对象$\mathcal{L}$是真实像素颜色C(r)与渲染颜色$\hat{\mathrm{C}}(\mathbf{r})$之间的均方误差,表示为
$\mathcal{L}_\mathrm{color}=\sum_{\mathbf{r}\in\mathcal{R}}|\mathrm{C}(\mathbf{r})-\hat{\mathbf{C}}(\mathbf{r})|_2^2,$ Eq.2
其中R为从相机中心到图像像素的所有光线的集合。
然而,基于密度的体绘制缺乏清晰的表面定义,这使得提取精确的几何形状变得困难。另外,有符号距离函数(Signed Distance Function, SDF)将曲面明确定义为零水平集,使得基于SDF的体绘制在曲面重建中更加有效。根据NeuS [45], 3D场景的属性包括带符号的距离和亮度,由几何网络f和亮度网络c参数化:
$s=f(\mathbf{x}),\quad\mathbf{c}=c(\mathbf{x},\mathbf{d}),$ Eq.3
其中几何网络f将空间位置x映射到其到对象的带符号距离f (x),而辐射网络c预测位置x和视图方向d的颜色,以模拟与视图相关的辐射。为了沿着射线r聚合采样点的带符号距离和颜色以进行像素颜色近似,我们使用了类似于NeRF的体渲染。关键的区别在于$\alpha_{i},$的公式,它是从带符号的距离f (x)而不是密度$\sigma_{i}$计算出来的
$\alpha_{i}=\max\left(\frac{\Phi_{s}\left(f(\mathbf{x}_{i})\right)-\Phi_{s}\left(f(\mathbf{x}_{i+1})\right)}{\Phi_{s}\left(f(\mathbf{x}_{i})\right)},0\right),$ Eq.4
$\Phi_s(x)=(1+e^{-sx})^{-1}$,1/s是一个可训练参数,表示$\Phi_s(x).$的标准差。
Anomaly Detection for Reflection Score
对于多视图重建,多视图一致性是精确重建曲面的保证。然而,对于反射像素,几何网络经常预测模糊的表面,这破坏了多视图的一致性。为了克服这个问题,我们建议通过反射感知光度损失来减少反射表面的影响,该损失自适应地降低分配给反射像素的权重。为了实现这一点,我们首先定义反射分数,它允许我们识别反射像素
一种naive的解决方案是将NeRF-W[27]中定义的不确定性作为反射评分。该方法将场景的radiance值建模为高斯分布,并将预测的不确定性视为方差。通过最小化高斯分布的负对数似然,大方差降低了具有高不确定性的像素的重要性。理想情况下,应该为反射像素分配较大的方差,以减弱其对重建的影响。然而,MLP学习到的隐式不确定性是在单个光线上定义的,而没有考虑多视图context。因此,如果没有明确的监督,它可能无法准确定位反射表面。
与NeRF-W[27]类似,我们也将渲染光线的颜色表述为高斯分布$\hat{\mathbf{C}}(\mathbf{r})\sim (\overline{\mathbf{C}}(\mathbf{r}),\overline{\mathbf{\beta}}^2(\mathbf{r}))$,其中$\mathrm{\overline{C}(r)}$和$\overline{\beta}^2(\mathbf{r})$分别是均值和方差。我们采用Eq.(1)来查询$\mathrm{\overline{C}(r)}$。然而,与NeRF-W不同的是,NeRF-W仅根据单个光线的信息定义隐式方差,我们基于多视图context显式定义方差。具体来说,我们利用多视图像素的颜色来确定相同的表面点的方差。
为了获得多视图像素颜色$\{\mathbf{C}_i(\mathbf{r})\}_{i=1}^N$,我们将曲面点x投影到所有N张图像$\{\mathbf{I}_i\}_{i=1}^N$上,并使用双线性插值得到相应的像素颜色$\{\hat{\mathbf{C}_i}(\mathbf{r})\}_{i=1}^N$,其中$\{\hat{\mathbf{C}_i}(\mathbf{r})\}_{i=1}^{N}= \left\{\mathbf{C}_i(\mathbf{r}),\{\mathbf{C}_j(\mathbf{r})\}_{j=1}^{N-1}\right\}$表示参考像素颜色和源像素颜色。为简单起见,省略下标,像素颜色C由
$\begin{aligned}\mathcal{G}&=\mathbf{K}\cdot\left(\mathbf{R}\cdot\mathbf{x}+\mathbf{T}\right),\\\mathbf{C}&=\operatorname{interp}(\mathbf{I},\mathcal{G}),\end{aligned}$ Eq.5
式中,interp为双线性插值,K为内标定矩阵,R为旋转矩阵,t为平移矩阵,·为矩阵乘法。
考虑到只有部分图像的局部区域包含反射,我们将反射定位视为异常检测问题,期望将反射表面视为异常并赋予较高的反射分数。为此,我们利用马氏距离[26]作为反射分数(即方差),通过异常检测器经验估计出视点相关反射分数$\cdot\overline{\beta}^{2}(\mathbf{r})$,如下所示:
$\overline{\beta}^{2}(\mathbf{r})=\gamma\frac{1}{N-1}\sum_{j=1}^{N-1}\sqrt{\left(\mathbf{C}_{i}(\mathbf{r})-\mathbf{C}_{j}(\mathbf{r})\right)^{T}\mathbf{\Sigma}^{-1}\left(\mathbf{C}_{i}(\mathbf{r})-\mathbf{C}_{j}(\mathbf{r})\right)},$Eq.6
其中γ为控制反射分数尺度的尺度因子,$\Sigma^{-1}$为经验协方差矩阵。由于反射并不占大多数训练图像的主导地位,如果当前渲染的像素颜色$\mathbf{C}_i(\mathbf{r})$受到反射的污染,则由于大多数相对散度变大,生成的反射分数也会变大。
然后,我们通过最小化类似于NeRF-W[27]和ActiveNeRF[32]的批次$\mathcal{R}$中射线r分布的负对数似然,将Eq.(2)中的光度损失扩展为反射感知的损失,如下所示:
$\mathcal{L}_{\mathrm{color}}=-\log p(\hat{\mathbf{C}}(\mathbf{r}))=\sum_{\mathbf{r}\in\mathcal{R}}\frac{|\mathbf{C}(\mathbf{r})-\overline{\mathbf{C}}(\mathbf{r})|_{2}^{2}}{2\overline{\beta}^{2}(\mathbf{r})}+\frac{\log\overline{\beta}^{2}(\mathbf{r})}{2}.$ Eq.7
由于${\overline{\beta}}^{2}(\mathbf{r})$是由Eq.(6)显式估计的,而不是通过MLP隐式学习,因此它是一个常数,可以从目标函数中去除。此外,根据之前的工作[45,52,9],我们使用L1损耗代替L2损耗进行多视图重建。最后,我们的反射感知光度损失是相当简单的公式为
$\mathcal{L}_{\mathrm{color}}=\sum_{\mathrm{r}\in\mathcal{R}}\frac{|\mathbf{C}(\mathbf{r})-\overline{\mathbf{C}}(\mathbf{r})|}{\overline{\beta}^2(\mathbf{r})}$ Eq.8
Visibility Identification for Reflection Score
使用源图像的所有像素颜色$\{\mathbf{C}_{j}(\mathbf{r})\}_{j=1}^{N-1}$计算反射分数时,假设表面上的点在所有源图像上都有有效的投影。然而,在实践中,由于自我聚焦,这种假设并不正确。如果该点在源图像中不可见,则投影的像素颜色没有意义,在式(6)中不应使用相应的像素颜色。
为了解决这个问题,我们设计了一个可见性识别模块,它利用中间重构网格来识别可见性,如图3所示。具体来说,给定一条射线$r_{i}$对应的像素$p_{i}$,则射线$r_{i}$上的隐式曲面可以根据采样点x的带符号距离表示为:$\hat{S}_i=\{\mathbf{x}\mid f(\mathbf{x})=0\}.$ Eq.9
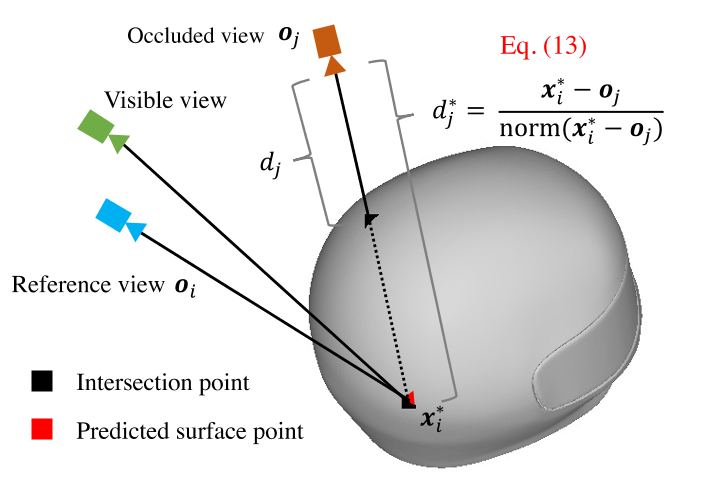
由于一条射线上有无数个点,我们需要对这条射线上的离散点进行采样。根据采样点和它们的符号距离,我们可以通过
$T_i=\left\{\mathbf{x}_j\mid f\left(\mathbf{x}_j\right)\cdot f\left(\mathbf{x}_{j+1}\right)<0\right\}.$ Eq.10
如果采样点$f(\mathbf{x}_j)$的符号与下一个采样点$f(\mathbf{x}_{j+1})$的符号不同,则区间$[\mathbf{x}_j,\mathbf{x}_{j+1}]$与曲面相交。交点集$\hat{S}_{i}$可由线性插值得到
$\hat{S}_i=\left\{\mathbf{x}\mid\mathbf{x}=\frac{f(\mathbf{x}_j)\mathbf{x}_{j+1}-f(\mathbf{x}_{j+1})\mathbf{x}_j}{f(\mathbf{x}_j)-f(\mathbf{x}_{j+1})},\mathbf{x}_j\in T_i\right\}$ Eq.11
实际上,射线$r_{i}$可以在多个表面与物体相交。对于我们的反射分数计算,只有第一个交集是有意义的,它被表示为
$\mathbf{x}_i^=\operatorname{argmin}\mathcal{D}(\mathbf{x},\mathbf{o}_i),$ Eq.12
$\mathbf{x}\in\hat{S}_{i}$和$\mathcal{D}(\cdot,\mathbf{o}_i)$分别表示点x和射线原点$r_{i}$之间的距离。
捕获预测的曲面点$\mathrm{x}_i^$后,我们可以计算该点与所有源相机位置$\{\mathbf{o}_{j}\}_{j=1}^{N-1}$之间的距离$\left\{d_j^\right\}_{j=1}^{N-1}$,如下所示:
$d_j^=\frac{\mathbf{x}_i^-\mathbf{o}_j}{\mathrm{norm}(\mathbf{x}_i^-\mathbf{o}_j)},$ Eq.13
其中norm表示将向量转换为单位向量的归一化操作。同时,我们通过光线投射计算所有源摄像机位置$\{\mathbf{o}_{j}\}_{j=1}^{N-1}$到中间重建网格的第一个交叉点的距离$\{d_j\}_{j=1}^{N-1}$[37]。基于这两个距离,源图像的可见性$\mathrm{I}_{j}$由
$v_j=\mathbb{I}(d_j^*\leq d_j)$ Eq.14
其中$\mathbb{I}(\cdot)$为指示函数。在近似可见性的基础上,我们剔除公式(6)中用于计算反射分数的不可见像素颜色$\{\mathbf{C}_j(\mathbf{r})\mid v_j=0\}$,然后将反射分数细化如下:
$\overline{\beta}^2(\mathbf{r})=\gamma\frac{1}{\sum_{j=1}^{N-1}v_j}\sum_{j=1}^{N-1}v_j\text{Mdis},$
$\mathbf{Mdis}=\sqrt{\left(\mathbf{C}_{i}(\mathbf{r})-\mathbf{C}_{j}(\mathbf{r})\right)^{T}\mathbf{\Sigma}^{-1}\left(\mathbf{C}_{i}(\mathbf{r})-\mathbf{C}_{j}(\mathbf{r})\right)}.$ Eq.15
我们在图4中提供了一些例子来说明估计的反射得分。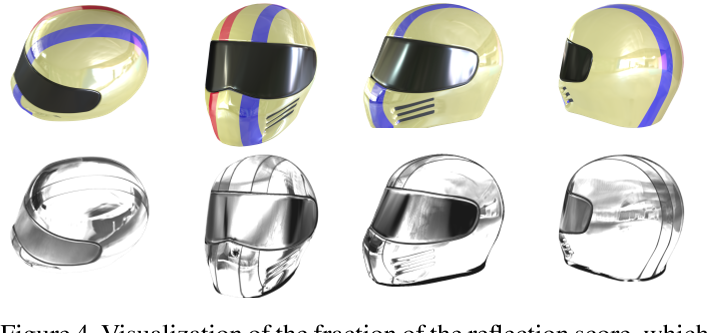
反射分数的可视化,可以定位反射面。黑色表示高分
Reflection Direction Dependent Radiance
如Ref-NeRF[43]所示,在反射场景中,根据反射方向调节亮度可以获得更精确的亮度场,这已被证明有利于在NeuralWarp中进行重建[7]。受此启发,我们将辐射网络重新参数化为表面法线反射方向的函数,公式(3)为
$\mathbf{c}=c(\mathbf{x},\hat{\mathbf{d}}),$ Eq.16
reflection direction: $\hat{\mathbf{d}}=2(-\mathbf{d}\cdot\mathbf{\hat{n}})\mathbf{\hat{n}}+\mathbf{d},$ Eq.17
surface normal: $\hat{\mathbf{n}}=\frac{\nabla f(\mathbf{x})}{||\nabla f(\mathbf{x})||}.$ Eq.18
与Ref-NeRF[43]相比,我们的框架中的反射方向更加精确,因为表面法线估计得很好,这导致了更精确的辐射场。与在其框架中忽略反射的NeuralWarp[7]相比,我们考虑了与视图相关的亮度,并估计了更准确的亮度场。结果表明,该方法对于具有反射的物体的多视图重建更为可靠和有前景
Optimization
损失函数:
$\mathcal{L}=\mathcal{L}_{\mathrm{color}}+\alpha\mathcal{L}_{\mathrm{eik}}.$
- 反射感知光度损失$\mathcal{L}_{\mathrm{color}}$ Eq.8
- $\mathcal{L}_{\mathrm{eik}}=\frac{1}{P}\sum_{i=1}^{P}\left(\left|\nabla f\left(x_{i}\right)\right|-1\right)^{2}.$
- $\alpha = 0.1$
Experimetns
Datasets
- Shiny Blender
- Blender
- SLF
- Bag of Chips
Evaluation Protocol.
- Chamfer Distance
- Shiny Blender
- MAE: mean angular error
- PSNR
Implementation Details
- same as NeuS
- 3090Ti 7h
Comparison with State-of-the-Art Methods
- IDR、UNISURF、VolSDF、NeuS
- NeuralWarp、Geo-NeuS
- Ref-NeRF、PhySG
- quantitative results
- qualitatively
Ablation Study