| Title | FreeNeRF: Improving Few-shot Neural Rendering with Free Frequency Regularization |
|---|---|
| Author | Jiawei Yang Marco Pavone Yue Wang |
| Conf/Jour | CVPR |
| Year | 2023 |
| Project | FreeNeRF: Frequency-regularized NeRF (jiawei-yang.github.io) |
| Paper | FreeNeRF: Improving Few-shot Neural Rendering with Free Frequency Regularization (readpaper.com) |
Frequency regularized NeRF (FreeNeRF)
T为正则化持续时间,t为当前训练迭代,L为输入位置编码的长度
How:
- High-frequency inputs cause the catastrophic failure in few-shot neural rendering.
- 位置编码中高频信号可以使高频分量更快收敛,但是过快收敛将导致少样本神经渲染中灾难性的过拟合
- 测试:将高频位置编码位设置为0,
pos_enc[int(L * x%): ] = 0,, L为位置编码的长度,x是可见比率
- Frequency regularization enjoys the benefits of both high-frequency and low-frequency signals.
- 频率正则化:根据训练时间steps,线性增加的频率mask,来正则化可见频谱。即刚开始使用低频,逐步增加高频信号的可见性
- 频率正则化有助于降低在开始时导致灾难性故障的过度拟合风险,并避免在最终导致过度平滑的欠拟合
- Occlusion regularization addresses the near-camera floaters.
- 遮挡正则化,对相机附近密集场进行乘法
Limitations
我们的FreeNeRF有两个限制
- 首先,较长的频率curriculum可以使场景更流畅,但可能会降低LPIPS分数,尽管达到了具有竞争力的PSNR分数。
- 其次,遮挡正则化会导致DTU数据集中近相机对象的过度正则化和不完整表示。每个场景调整正则化范围可以缓解这个问题,但我们选择不在本文中使用它。
Conclusion
我们提出了FreeNeRF,一种简化的少镜头神经渲染方法。我们的研究揭示了输入频率与少镜头神经渲染失败之间的深层关系。一个简单的频率正则化器可以彻底解决这个挑战。FreeNeRF在多数据集上的性能优于现有的最先进的方法,开销最小。
我们的研究结果为未来的研究提供了几个方向。例如,将FreeNeRF应用于受高频噪声影响的其他问题是有趣的,例如NeRF in the wild,in the dark,以及野外更具有挑战性的图像,例如来自自动驾驶场景的图像。
此外,在附录中,我们展示了频率正则化的NeRF产生更平滑的正频估计,这可以促进处理光滑表面的应用,如RefNeRF[32]。我们希望我们的工作能激发对少镜头神经渲染的进一步研究,并在神经渲染中更普遍地使用频率正则化。
AIR
具有稀疏输入的新颖视图合成是神经辐射场 (NeRF) 的一个具有挑战性的问题。最近的工作通过引入外部监督(例如预训练模型和额外的深度信号)或使用非平凡的基于补丁的渲染来缓解这一挑战。在本文中,我们提出了频率正则化 NeRF (FreeNeRF),这是一个令人惊讶的简单基线,在对普通 NeRF 进行最小修改的情况下优于以前的方法。
我们分析了少镜头神经渲染的关键挑战,发现频率在NeRF的训练中起着重要作用。基于该分析,我们提出了两个正则化项:一个用于正则化 NeRF 输入频率范围,另一个用于惩罚近相机密度场。这两种技术都是”free lunches”,无需额外的计算成本。
我们证明了即使只有一行代码更改,原始 NeRF 也可以在少样本设置中实现与其他复杂方法相似的性能。FreeNeRF 在不同的数据集上实现了最先进的性能,包括 Blender、DTU 和 LLFF。我们希望这个简单的基线能够激发人们重新思考频率在 NeRF 训练中的基本作用,在低数据模式下和更高模式下
Introduction
- NeRF稀疏视图
- 迁移学习方法
- PixelNerf
- MVSNeRF
- 深度监督方法
- 基于补丁的正则化方法
- 语义一致性正则化
- 几何正则化
- 外观正则化
- 迁移学习方法
我们提出两个正则化项:
- 频率正则化
- 遮挡正则化
我们的方法FreeNeRF特点:
- 无依赖,不需要昂贵的预训练,也不需要额外的监督信号
- 无开销,不需要额外的基于补丁的正则化训练时间
贡献:
- 我们揭示了少镜头神经渲染失败与位置编码频率之间的联系,并通过实证研究进一步验证了这一点,并通过我们提出的方法解决了。据我们所知,我们的方法是首次尝试从频率的角度解决少镜头神经渲染。
- 我们从稀疏输入中确定了学习NeRF的另一个常见失败模式,并通过新的遮挡正则化器来缓解它。这个正则化器有效地提高了性能并泛化了数据集。
- 结合,我们引入了一个简单的基线 FreeNeRF,它可以通过几行代码修改来实现,同时优于以前的最先进方法。我们的方法是无依赖和无开销的,使其成为这个问题的实用且有效的解决方案。
Related Work
Neural fields 神经场[36]使用深度神经网络将2D图像或3D场景表示为连续函数。开创性的工作神经辐射场(Neural Radiance Fields, NeRF)[21]在各种应用中得到了广泛的研究和推进[2,3,32,19,23,13,25],包括新型视图合成[21,18]、3D生成[25,10]、变形[23,26,28]、视频[15,35,7,24,14]。尽管取得了巨大的进步,NeRF仍然需要数百个输入图像来学习高质量的场景表示; 它无法用一些输入视图(例如3,6和9视图)合成新的视图,从而限制了它在现实世界中的潜在应用。
Few-shot Neural Rendering. 许多作品试图通过利用额外的信息来解决具有挑战性的少数镜头神经渲染问题。例如,外部模型可用于获得归一化——流正则化[22]、感知正则化[38]、深度监督[29,6,34]和跨视图语义一致性[11]。另一项研究[5,37,4]试图通过在一个大型的、精心策划的数据集上训练来学习可转移模型,而不是使用外部模型。最近的研究认为几何是少镜头神经渲染中最重要的因素,并提出几何正则化[22,1,8]以获得更好的性能。然而,这些方法需要在定制的多视图数据集上进行昂贵的预训练[5,37,4]或昂贵的训练时间补丁渲染[11,22,1,8],这在方法、工程实施和训练预算方面带来了巨大的开销。在这项工作中,我们表明,通过结合我们的频率正则化和遮挡正则化,简单的NeRF可以通过最小的修改(几行代码)出奇地好地工作。与大多数以前的方法不同,我们的方法保持了与原始NeRF相同的计算效率
Frequency in neural representations 位置编码是NeRF成功的核心[21,31]。先前的研究[31,30]表明,神经网络通常难以从低维输入中学习高频函数。用不同频率的正弦函数编码输入可以缓解这个问题。最近的研究表明,在非刚性场景变形[23]、束调整[16]、曲面重构[33]和更宽频带的拟合函数[9]等不同应用中,逐渐增加输入频率是有好处的。我们的工作利用频率课程来解决少数镜头的神经渲染问题。值得注意的是,我们的方法不仅证明了频率正则化在从稀疏输入中学习方面的惊人有效性,而且揭示了这个问题背后的失效模式以及频率正则化为什么有帮助。
Method
Preliminaries
Neural radiance fields. 神经辐射场(NeRF)[21]使用多层感知器(MLP)将场景表示为体积密度场σ和场景中每个点的相关RGB值c。它以三维坐标$\mathrm{x~\in~\mathbb{R}^3}$和观看方向单位矢量$\mathbf{d}\in\mathbb{S}^{2},$作为输入,输出相应的密度和颜色。在其最基本的形式中,NeRF学习一个连续函数$f_\theta(\mathbf{x},\mathbf{d})=(\sigma,\mathbf{c})$,其中θ表示MLP参数。
Positional encoding. 直接优化原始输入(x, d)上的NeRF通常会导致合成高频细节的困难[31,21]。为了解决这个问题,最近的研究使用不同频率的正弦函数将输入映射到高维空间[21]
$\gamma_{L}(\mathbf{x})=\left[\sin(\mathbf{x}),\cos(\mathbf{x}),…,\sin(2^{L-1}\mathbf{x}),\cos(2^{L-1}\mathbf{x})\right],$ Eq.1
其中L是一个控制最大编码频率的超参数,对于坐标x和方向向量d可能会有所不同。一种常见的做法是将原始输入与频率编码输入连接起来:$\mathbf{x’}=[\mathbf{x},\gamma_L(\mathbf{x})]$ Eq.2,此连接应用于坐标输入和视图方向输入。
Rendering. 为了在NeRF中渲染一个像素,从相机原点o沿着方向d投射一条射线$\mathbf{r}(t)=\mathbf{o}+t\mathbf{d}$穿过像素,其中t是到原点的距离。在投射光线的近界和远界$[t_\mathrm{near},t_\mathrm{far}]$内,NeRF使用K个采样点$\mathbf{t}_{K}=\{t_{1},\ldots,t_{K}\}$的求积来计算该光线的颜色:
$\hat{\mathbf{c}}(\mathbf{r};\theta,\mathbf{t}_K)=\sum_{K}T_k(1-\exp(-\sigma_k(t_{k+1}-t_k)))\mathbf{c_k},$
$\text{with}\quad T_{k}=\exp\left(-\sum_{k’<k}\sigma_{k}^{\prime}\left(t_{k’+1}-t_{k’}\right)\right),$ Eq.3
$\hat{\mathbf{c}}(\mathbf{r};\theta,\mathbf{t}_K)$为最终的积分色。注意,采样点$\mathbf t_{K}$是按远近顺序排列的,即指数k较小的点离相机原点更近。
Frequency Regularization
少镜头神经渲染最常见的失效模式是过拟合。NeRF从一组没有明确的3D几何图形的2D图像中学习3D场景表示。通过优化2D投影视图中的外观,隐式地学习3D几何。然而,由于只有少数输入视图,NeRF很容易过度拟合这些2D图像,损失很小,同时不能以多视图一致的方式解释3D几何。从这些模型中综合新的观点会导致系统失败。如图1左侧所示,在合成新视图时,没有NeRF模型能够成功恢复场景几何形状。
高频输入可能会加剧少数镜头神经渲染中的过拟合问题。[31]表明,高频映射使高频分量的收敛速度更快。然而,高频上的过快收敛阻碍了NeRF对低频信息的探索,并显著地使NeRF倾向于不需要的高频伪影(图1中的喇叭和房间示例)。在少拍场景中,NeRF对易受影响的噪声更敏感,因为需要学习相干几何的图像更少。因此,我们假设高频成分是在少量神经渲染中观察到的失效模式的主要原因。我们在下面提供了经验证据
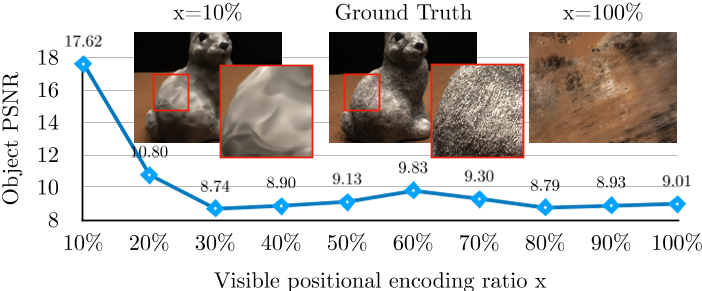
我们研究了当输入由不同数量的频带编码时,普通NeRF是如何执行的。为了实现这一点,我们使用掩码(集成)位置编码来训练mipNeRF[2]。具体来说,我们设置pos enc[int(L*x%]):]=0,其中L表示经过位置编码(Eq.(1))后的频率编码坐标的长度,x为可见比。我们在这里简单地说明我们的观察结果,并把实验的细节推迟到§4.1。图2显示了DTU数据集在3个输入视图设置下的结果。正如预期的那样,我们观察到当向模型提供更高频率的输入时,mipNeRF的性能显着下降。当使用总嵌入位的10%时,mipNeRF实现了17.62的高PSNR,而普通mipNeRF本身仅实现9.01的PSNR(在100%可见比下)。这两种模型之间的唯一区别是是否使用掩码位置编码。虽然去除高频成分的很大一部分避免了在训练开始时的灾难性故障,但它不会导致竞争性的场景表示,因为渲染的图像通常是过度平滑的(如图2放大补丁所示)。尽管如此,值得注意的是,在少数场景中,使用低频输入的模型可能比使用高频输入的模型产生更好的表示。
基于这一经验发现,我们提出了一种频率正则化方法。给定长度为L + 3的位置编码(Eq.(2)),我们使用线性增加的频率掩码α来根据训练时间步长调节可见频谱,如下所示:
$\gamma_{L}^{\prime}(t,T;\mathbf{x})=\gamma_{L}(\mathbf{x})\odot\mathbf{\alpha}(t,T,L),$ Eq.4
$\text{with }\alpha_i(t,T,L)=\begin{cases}1&\text{if }i\le\frac{t\cdot L}{T}+3\\\dfrac{t\cdot L}{T}-\lfloor\dfrac{t\cdot L}{T}\rfloor&\text{if }\frac{t\cdot L}{T}+3
式中$\alpha_i(t,T,L)$为$\alpha(t,T,L)$的第i位值,t和T分别为频率正则化的当前训练迭代和最终迭代。具体地说,我们从没有位置编码的原始输入开始,随着训练的进行,每次线性增加3位的可见频率。这个时间表也可以简化为一行代码,如图1所示。我们的频率正则化绕过了训练开始时不稳定、易受影响的高频信号,逐步提供NeRF高频信息,避免过平滑。
我们注意到,我们的频率正则化与其他工作中使用的粗到细频率调度有一些相似之处[23,16]。与他们不同的是,我们的工作侧重于少镜头神经渲染问题,揭示了高频输入引起的灾难性故障模式及其对该问题的影响。
Occlusion Regularization
频率正则化并不能解决少镜头神经渲染中的所有问题。由于训练视图的数量有限和问题的不适定性质,在新视图中可能仍然存在某些特征伪象。这些失效模式通常表现为靠近相机的“墙壁”或“漂浮物”,如图3底部所示。即使有足够数量的训练视图[3],仍然可以观察到这样的工件。为了解决这些问题,Mip-NeRF 360[3]提出了失真损失。然而,我们的实验表明,这种正则化在很少的镜头设置中没有帮助,甚至可能加剧问题。
我们发现大多数的失败模式源自训练视图中重叠最少的区域。图3显示了3个训练视图和2个带有“白墙”的新视图的示例。为了演示(图3中的(a)和(b)),我们手动标注了训练视图中重叠最少的区域。由于可用信息极其有限(一次性),这些区域很难从几何角度进行估计。因此,NeRF模型将这些未开发区域解释为位于相机附近的密集体积漂浮物。我们怀疑在[3]中观察到的漂浮物也来自这些重叠最少的区域。
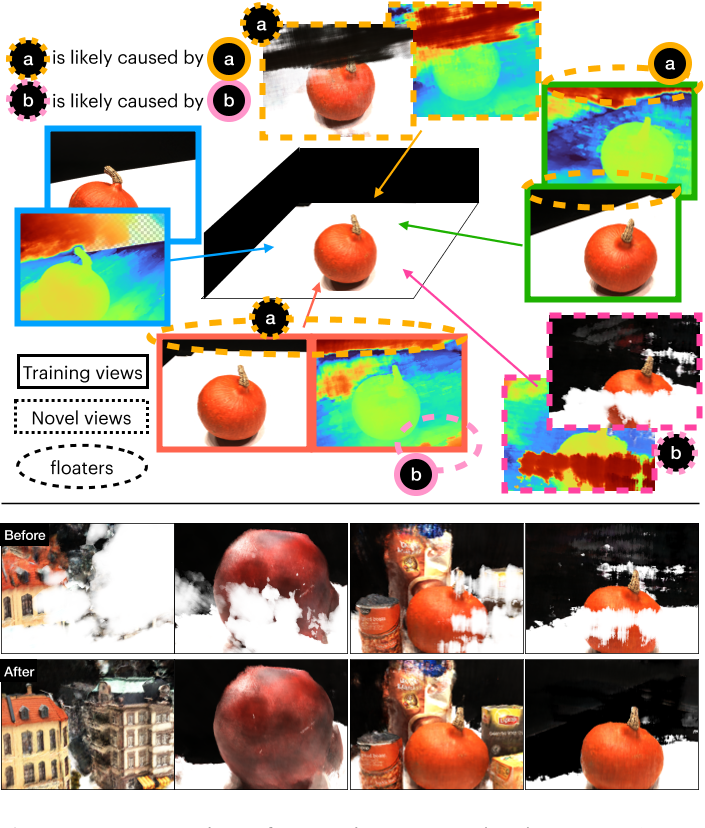
遮挡正则化示意图。我们展示了3个训练视图(实心矩形)和2个新视图(虚线矩形),这些视图由频率正则化的NeRF渲染。在训练视图(虚线圈)中,新视图中的漂浮物似乎是靠近相机的密集场,因此我们可以直接惩罚它们,而不需要在[11,22]中进行昂贵的新视图渲染。
如上所述,新视图中漂浮物和墙壁的存在是由不完善的训练视图引起的,因此可以在训练时直接解决,而不需要进行新姿态采样[22,11,37]。为此,我们提出了一种简单而有效的“遮挡”正则化方法,对相机附近的密集场进行惩罚。我们定义: $\mathcal{L}_{occ}=\frac{\sigma_{K}^{\mathsf{T}}\cdot\mathrm{m}_{K}}{K}=\frac{1}{K}\sum_{K}\sigma_{k}\cdot m_{k},$ Eq.6
其中$m_k$是一个二进制掩模向量,它决定了一个点是否会被惩罚,$\sigma_{K}$表示沿着射线采样的K个点的密度值,其顺序从近到远。为了减少相机附近的固体漂浮物,我们将指数 M以下的$m_k$值(正则化范围),设置为1,其余为0。闭塞正则化损失易于实现和计算。
Experiments
Datasets & metrics
- NeRF Blender合成数据集(Blender) DietNeRF
- DTU数据集 RegNeRF
- LLFF数据集 RegNeRF
- metrics:PSNR, SSIM和LPIPS
- and $\mathrm{MSE~=~10^{-PSNR/10}},$$\sqrt{1-\mathrm{SSIM}},$LPIPS,
Implementations
直接改进NeRF和mipNeRF
Hyper-parameters
- $T=\lfloor90\%*\text{total-iters}\rfloor$ to 3-view setting
- $T=\lfloor70\%*\text{total-iters}\rfloor$ to 6-view setting
- $T=\lfloor20\%*\text{total-iters}\rfloor$ to 9-view setting
- $\mathcal{L}_{occ}$ 使用0.01权重
- LLFF和Blender的正则化范围设置为M = 20, DTU的正则化范围设置为M = 10
Comparing methods.
除非另有说明,否则我们直接使用DietNeRF[11]和RegNeRF[22]中报告的结果进行比较,因为我们的方法是使用它们的代码库实现的。我们还包括我们的复制结果供参考。
Comparison
Ablation Study
Frequency curriculum.
Occlusion regularization