| Title | SparseNeuS: Fast Generalizable Neural Surface Reconstruction from Sparse Views |
|---|---|
| Author | Xiaoxiao Long Cheng Lin Peng Wang Taku Komura Wenping Wang |
| Conf/Jour | ECCV |
| Year | 2022 |
| Project | SparseNeuS: Fast Generalizable Neural Surface Reconstruction from Sparse Views (xxlong.site) |
| Paper | SparseNeuS: Fast Generalizable Neural Surface Reconstruction from Sparse views (readpaper.com) |
从仅2~3张的稀疏输入中重建表面
- 首先,我们提出了一个多层几何推理框架,以粗到细的方式恢复表面。
- 其次,我们采用了一种多尺度颜色混合方案,该方案联合评估局部和背景亮度一致性,以获得更可靠的颜色预测。
- 第三,采用一致性感知的微调方案,控制遮挡和图像噪声引起的不一致区域,得到准确、干净的重建。
Conclusion
提出了一种新的基于神经渲染的表面重建方法SparseNeuS,用于从多视图图像中恢复表面。我们的方法可以推广到新的场景,并产生高质量的稀疏图像重建,这是以前的作品[44,49,32]所难以做到的。因此,为了使我们的方法推广到新的场景,我们引入了几何编码体来编码通用几何推理的几何信息。此外,针对稀疏视图设置困难的问题,提出了一系列策略。
- 首先,我们提出了一个多层几何推理框架,以粗到细的方式恢复表面。
- 其次,我们采用了一种多尺度颜色混合方案,该方案联合评估局部和背景亮度一致性,以获得更可靠的颜色预测。
- 第三,采用一致性感知的微调方案,控制遮挡和图像噪声引起的不一致区域,得到准确、干净的重建。
实验表明,该方法在重建质量和计算效率方面都优于目前的方法。由于采用了符号距离场,我们的方法只能产生闭面重构。未来可能的方向包括利用其他表示,如无符号距离场来重建开放表面物体。
AIR
介绍了一种新的基于神经渲染的多视图图像表面重建方法——SparseNeuS。当只提供稀疏图像作为输入时,这项任务变得更加困难,在这种情况下,现有的神经重建方法通常会产生不完整或扭曲的结果。此外,它们无法推广到未见过的新场景,阻碍了它们在实践中的应用。相反,SparseNeuS可以泛化到新的场景,并且可以很好地处理稀疏图像(少至2或3张)。
SparseNeuS采用有符号距离函数(SDF)作为表面表示,并通过引入几何编码体从图像特征中学习泛化先验,用于通用表面预测。此外,引入了几种策略来有效地利用稀疏视图进行高质量的重建,包括:
1)多级几何推理框架,以粗到精的方式恢复表面;
2)多尺度颜色混合方案,实现更可靠的颜色预测;
3)一致性感知微调方案,控制遮挡和噪声引起的不一致区域。
大量的实验表明,我们的方法不仅优于最先进的方法,而且具有良好的效率、通用性和灵活性。
Introduction
从多视图图像中重建三维几何结构是计算机视觉中的一个基本问题,已经被广泛研究了几十年。传统的多视图立体方法[2,8,36,18,37,7,19]通过在输入图像中寻找相应的匹配来重建三维几何形状。然而,当只有一组稀疏的图像作为输入时,图像噪声、弱纹理和反射使得这些方法难以建立密集和完整的匹配。
随着神经隐式表示的最新进展,神经表面重建方法[44,50,49,32]利用神经渲染来共同优化隐式几何和辐射场,通过最小化渲染视图和地面真实视图的差异。虽然这些方法可以产生似是而非的几何形状和逼真的新颖视图,但它们有两个主要的局限性。
- 首先,现有的方法严重依赖于大量的输入视图,即密集视图,这在实践中通常是不可用的。
- 其次,它们需要耗时的逐场景优化重建,因此无法推广到新的场景。为了使这种重建方法适用于实际应用,需要解决这些限制。
我们提出了一种新的多视图表面重建方法SparseNeuS,它具有两个明显的优点:
- 它具有良好的泛化能力;
- 只需要一组稀疏的图像(少则2 ~ 3张)即可成功重建。
SparseNeuS通过从图像特征中学习可泛化先验并分层地利用稀疏输入中编码的信息来实现这些目标。
为了学习可泛化先验,根据MVSNerf[3],我们构建了一个几何编码体,该编码体聚集了来自多视图输入的2D图像特征,并使用这些信息潜在特征来推断3D几何。因此,我们的曲面预测网络采用混合表示作为输入,即xyz坐标和来自几何编码体的相应特征,来预测重建曲面的网络编码符号距离函数(SDF)。
我们的pipeline中最关键的部分是如何有效地整合来自稀疏输入图像的有限信息,通过神经渲染获得高质量的表面。为此,我们介绍了一些应对这一挑战的策略。
- 首先是一种多级几何推理方案,由粗到细逐级构造曲面。我们使用级联体编码结构,即编码相对全局特征的粗体来获得高级几何形状,粗体引导的细体来细化几何形状。每个场景的微调过程被进一步纳入到该方案中,该方案以推断的几何形状为条件,以构建细微的细节来生成更细粒度的表面。这种多层次的方案将高质量的重建任务分为几个步骤。每一步都是基于前一步的几何图形,重点是构建更精细的细节。此外,由于该方案的层次性,大大提高了重建效率,因为可以丢弃大量远离粗糙表面的样本,从而不会增加精细几何推理的计算负担。
- 我们提出的第二个重要策略是用于新视图合成的多尺度颜色弯曲方案。鉴于稀疏图像中的信息有限,网络将难以直接回归准确的颜色以呈现新视图。因此,我们通过预测输入图像像素的线性混合权重来获得颜色来缓解这个问题。具体来说,我们采用基于像素和基于补丁的混合来共同评估局部和上下文的亮度一致性。当输入是稀疏的时,这种多尺度混合方案产生更可靠的颜色预测。
- 多视图3D重建的另一个挑战是,由于遮挡或图像噪声,3D表面点在不同视图之间通常没有一致的投影。在输入视图数量较少的情况下,几何推理对每个图像的依赖性进一步增加,从而加剧了问题并导致几何变形。为了应对这一挑战,我们在微调阶段提出了一致性感知的微调方案。该方案自动检测缺乏一致投影的区域,并在优化中排除这些区域。事实证明,该策略有效地使微调表面不易受遮挡和噪声的影响,从而更准确,更清洁,有助于高质量的重建。
我们在DTU[11]和BlendedMVS[48]数据集上评估了我们的方法,并表明我们的方法在定量和定性上都优于最先进的无监督神经隐式表面重建方法
In Summary
- 提出了一种基于神经绘制的表面重建方法。我们的方法学习了跨场景的可泛化先验,因此可以泛化到具有高质量几何结构的新场景进行3D重建。
- 我们的方法能够从稀疏的图像集(少至2或3张图像)进行高质量的重建。这是通过使用三种新策略有效地从稀疏输入图像推断3D表面来实现的:
- a)多级几何推理multi-level geometry reasoning;
- b)多尺度配色multi-scale color blending;
- c)一致性意识微调。consistency-aware fine-tuning
- 我们的方法在重建质量和计算效率方面都优于最先进的方法
Related Work
- Multi-view stereo(MVS)
- 经典的MVS方法利用各种3D表示进行重建,例如:基于体素网格的[12,13,15,18,37,40],基于3D点云的[7,19],以及基于深度图的[2,8,36,42,47,10,27,26,25]。与体素网格和3D点云相比,深度图更加灵活,更适合并行计算,因此基于深度图的方法是最常用的,如著名的COLMAP[36]方法。基于深度图的方法首先估计每个图像的深度图,然后利用滤波操作将深度图融合在一起,形成全局点云,然后使用筛选泊松曲面重建[16]等网格算法进行进一步处理。这些方法在密集捕获的图像上取得了很好的效果。然而,由于图像数量有限,这些方法对图像噪声、弱纹理和反射更加敏感,使得这些方法难以产生完整的重建
- Neural surface reconstruction
- 近年来,三维几何的神经隐式表示已成功应用于形状建模[1,4,9,28,33,29]、新视图合成[39,24,30,21,34,38,38,43]和多视图三维重建[14,50,31,17,22,44,49,32,32,52,52,6]。
- 对于多视图重建任务,三维几何图形由神经网络表示,神经网络输出占用场或符号距离函数(SDF)。一些方法利用表面渲染[31]进行多视图重建,但它们总是需要额外的对象掩模[50,31]或深度先验[52],这在实际应用中效率较低。
- 为了避免额外的掩码或深度先验,一些方法[44,49,32,6]利用体绘制进行重建。然而,它们也严重依赖于大量的图像来执行耗时的逐场景优化,因此无法推广到新的场景。
- 在泛化方面,已有一些成功的神经渲染尝试[51,45,3,23,5]。这些方法以稀疏视图为输入,利用图像的亮度信息生成新的视图,可以推广到未见场景。虽然这些方法可以生成合理的合成图像,但提取的几何图形往往存在噪声、不完整性和失真等问题。
Method
给定几个(即三个)具有已知相机参数的视图,我们提出了一种分层恢复表面并跨场景进行泛化的新方法。如图2所示,我们的管道可以分为三个部分:
(1)几何推理。SparseNeuS首先构建级联几何编码体,对局部几何表面信息进行编码,并以粗到细的方式从体积中恢复表面(参见3.1节)。
(2)外观预测。SparseNeuS利用多尺度颜色混合模块通过汇总输入图像的信息来预测颜色,然后将估计的几何形状与预测的颜色相结合,使用体绘制来渲染合成视图(参见3.2节)。
(3)逐场景微调。最后,提出了一种一致性感知的微调方案,以进一步改善获得的具有细粒度细节的几何形状(参见3.3节)。
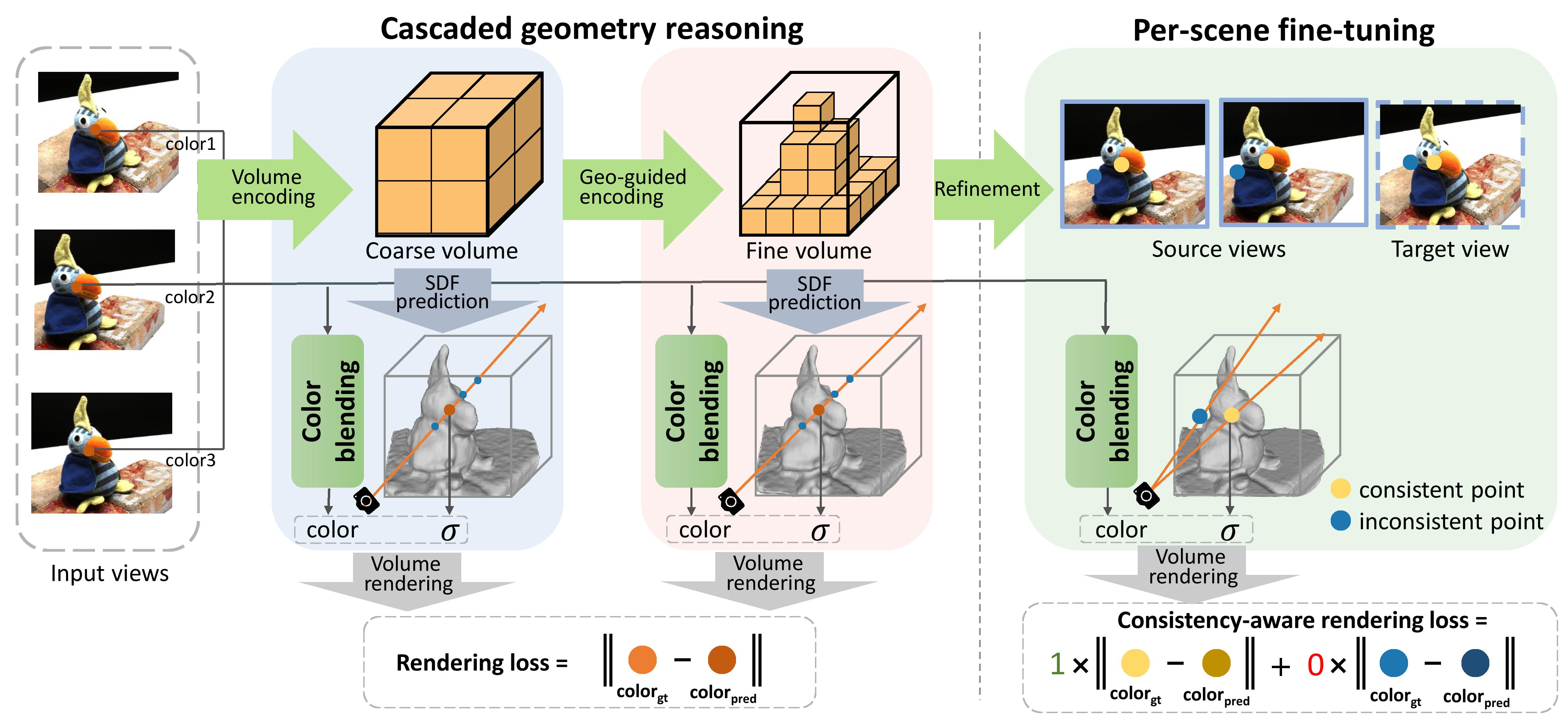
SparseNeuS概述。级联几何推理方案首先构建一个编码相对全局特征的粗体来获得基本几何,然后在粗层的引导下构建一个精细体来细化几何。最后,使用一致性感知微调策略来添加微妙的几何细节,从而产生具有细粒度表面的高质量重建。特别地,利用多尺度颜色混合模块进行更可靠的颜色预测
Geometry reasoning
SparseNeuS构建两种不同分辨率的级联几何编码体进行几何推理,聚合图像特征对局部几何信息进行编码。该方法首先从低分辨率的几何编码体中提取粗几何,然后用粗几何来指导精细层次的几何推理。
几何编码体积
对于N幅输入图像$\{I_i\}_{i=0}^{N-1}$捕获的场景,我们首先估计一个能够覆盖感兴趣区域的边界框。在居中输入图像的相机坐标系中定义边界框,然后网格化成规则体素。为了构造几何编码体M,通过二维特征提取网络从输入图像$\{I_i\}_{i=0}^{N-1}$中提取二维特征映射$\{F_{i}\}_{i=0}^{N-1}$。接下来,利用一张图像$I_{i}$的相机参数,将边界框的每个顶点v投影到每个特征映射$F_{i}$上,通过插值得到其特征$F_i(\pi_i(v))$,其中$\pi_i(v)$表示v在特征图$F_{i}$上的投影像素位置。为简便起见,我们将$F_i(\pi_i(v))$缩写为$F_{i}(v).$。
使用每个顶点的所有投影特征$\{F_i(v)\}_{i=0}^{N-1}$构造几何编码体积M。按照之前的方法[46,3],我们首先计算顶点所有投影特征的方差来构建cost 体积B,然后应用稀疏的3D CNN $\mathbb{\Psi}$对代价体积B进行聚合,得到几何编码体积M:
$M=\psi(B),\quad B(v)=\mathrm{Var}\left(\{F_{i}(v)\}_{i=0}^{N-1}\right),$
其中Var为方差运算,计算每个顶点v的所有投影特征$\{F_i(v)\}_{i=0}^{N-1}$的方差。
表面提取
给定任意三维位置q, MLP网络$f_{θ}$以三维坐标及其对应的几何编码体M (q)的插值特征的组合作为输入,预测用于曲面表示的有符号距离函数(SDF) s(q)。其中,对其三维坐标进行位置编码PE,曲面提取操作表示为:$s(q)=f_\theta(\operatorname{PE}(q),M(q)).$
级联体积方案
为了平衡计算效率和重建精度,SparseNeuS构建了两种分辨率的级联几何编码体,以粗到精的方式进行几何推理。首先构建粗糙几何编码体来推断基本几何,该编码体呈现场景的全局结构,但由于体积分辨率有限,精度相对较低。在得到的粗几何结构的指导下,构建精细几何编码体,进一步细化表面细节。在精细级体积中,可以丢弃许多远离粗糙表面的顶点,这大大减少了计算内存负担,提高了效率。
Appearance prediction
给定方向为d的射线上的任意3D位置q,我们通过汇总来自输入图像的外观信息来预测其颜色。在稀疏输入图像信息有限的情况下,网络很难直接回归颜色值来呈现新视图。与之前的作品[51,3]不同,sparseneus通过预测输入图像的混合权重来生成新的颜色。首先将一个位置q投影到输入图像上,得到相应的颜色$\{I_i(q)\}_{i=0}^{N-1}.$。然后使用估计的混合权值将来自不同视图的颜色混合在一起作为q的预测颜色。
混合权重
生成混合权值$\{w_i^q\}_{i=0}^{N-1}$的关键是考虑输入图像的摄影一致性。我们将q投影到特征映射$\{F_{i}\}_{i=0}^{N-1}$上,使用双线性插值提取相应的特征$\{F_i(q)\}_{i=0}^{N-1}$。此外,我们从不同的角度计算特征$\{F_i(q)\}_{i=0}^{N-1}$的均值和方差,以获取全局摄影一致性信息。每个特征$F_{i}(q)$与均值和方差连接在一起,然后输入到一个微小的MLP网络中生成一个新的特征$F_i^{\prime}(q)$。接下来,我们将新特征$F_i^{\prime}(q)$,查询射线相对于第i个输入图像的观察方向的观察方向$\Delta d_{i}=d{-}d_{i},$,以及三线性插值的体积编码特征M(q)输入MLP网络$f_c$,以生成混合权值:$w_{i}^{q}=f_{c}(F_{i}^{\prime}(q),M(q),\Delta d_{i}).$。最后,使用Softmax算子对混合权值$\{w_i^q\}_{i=0}^{N-1}$进行归一化。
基于像素的颜色混合
利用得到的混合权值,预测3D位置q的color $c_q$为其投影颜色$\{I_i(q)\}_{i=0}^{N-1}$在输入图像上的加权和。为了渲染查询光线的颜色,我们首先预测在光线上采样的3D点的颜色和SDF值。使用基于SDF的体绘制[44],将采样点的颜色和SDF值聚合以获得光线的最终颜色。由于查询光线的颜色对应于合成图像的一个像素,因此我们将此操作命名为基于像素的混合。尽管对基于像素的混合所呈现的颜色的监督已经诱导出有效的几何推理,但像素的信息是局部的,缺乏上下文信息,因此当输入是稀疏的时,通常会导致不一致的表面斑块。
基于补丁的颜色混合
受经典patch 匹配的启发,我们考虑强制合成颜色和gt颜色上下文一致;即不仅在像素级,而且在贴片级。要渲染大小为k × k的patch的颜色,一种幼稚的实现是使用体渲染查询$k^2$射线的颜色,这会导致大量的计算量。因此,我们利用局部曲面假设和单应性变换来实现更有效的实现。
关键思想是估计采样点的局部平面,从而有效地导出局部patch。给定一个采样点q,我们利用SDF网络s(q)的性质,通过计算空间梯度来估计法向$n_{q}$,即$n_q=\nabla s(q)$。然后,我们对局部平面$(q,n_q)$上的一组点进行采样,将采样点投影到每个视图上,并对每个输入图像进行插值得到颜色。局部平面上的所有点与q共享相同的混合权值,因此只需要查询一次混合权值。利用局部平面假设,考虑查询三维位置的邻近几何信息,对局部补丁的上下文信息进行编码,增强了查询三维位置的几何一致性。通过采用基于patch的体绘制,合成区域比单个像素包含更多的全局信息,从而产生更有信息量和一致性的形状上下文,特别是在纹理较弱和强度变化的区域。
体积渲染
为了绘制经过场景的光线r的像素色C(r)或补丁色P (r),我们查询光线上M个样本的像素色、补丁色$p_i$和sdf值$s_i$,然后利用Neus中体渲染函数将sdf值$s_i$转换为密度$σ_i$。最后,密度被用来沿着射线积累基于像素和基于补丁的颜色:$U(r)=\sum_{i=1}^MT_i\left(1-\exp\left(-\sigma_i\right)\right)u_i,\quad\mathrm{where}\quad T_i=\exp\left(-\sum_{j=1}^{i-1}\sigma_j\right)$
其中U (r)表示C (r)或P (r), $u_{i}$表示第i个样本在射线上基于像素的颜色$c_{i}$或基于patch的颜色$p_{i}$。
Per-scene fine-tuning
利用可推广的先验和有效的几何推理框架,在给定新场景的稀疏图像的情况下,SparseNeuS已经可以通过快速网络推理恢复几何表面。然而,由于稀疏输入视图中的信息有限,以及不同场景的高度多样性和复杂性,通用模型获得的几何形状可能包含不准确的异常值,缺乏微妙的细节。
因此,我们提出了一种新的微调方案,该方案以推断的几何形状为条件,重构细微细节并生成更细粒度的表面。由于网络推理给出的初始化,每个场景的优化可以快速收敛到一个高质量的曲面。
精调网络Fine-tuning networks
在微调中,我们直接优化得到的精细级几何编码体积和有符号距离函数(SDF)网络$f_θ$,而丢弃二维特征提取网络和三维稀疏CNN网络。
此外,在通用设置中使用的基于CNN的混合网络被一个微小的MLP网络所取代。虽然基于CNN的网络也可以用于逐场景微调,但通过实验,我们发现一个新的微型MLP可以加速微调而不会损失性能,因为MLP比基于CNN的网络小得多。MLP网络仍然输出混合权重$\{w_{i}^{q}\}_{i=0}^{N-1}$查询的3D位置q, 但是需要输入的组合3d坐标q,表面法向$n_q$,射线方向d, 预测SDFs(q), 和几何编码体积的插值特征M(q)。特别, 位置编码PE应用于3d位置q和射线方向d。
MLP网络$f_{c}^{\prime}$的定义是:$\{w_i^q\}_{i=0}^{N-1}=f_c^{\prime}(\mathrm{PE}(q),\mathrm{PE}(d),n_q,s(q),M(q))$,其中$\{w_i^q\}_{i=0}^{N-1}$为预测的混合权值,N为输入图像的个数。
一致性感知的颜色损失
我们观察到,在多视图立体中,由于投影可能被图像噪声遮挡或污染,3D表面点在不同视图之间往往没有一致的投影。因此,这些区域的误差处于次优状态,并且这些区域的预测曲面总是不准确和扭曲的。为了解决这个问题,我们提出了一种一致性感知的颜色损失来自动检测缺乏一致投影的区域,并在优化中排除这些区域:
其中r是一条查询射线,$\mathbb{R}$是所有查询射线的集合,$O (r)$是通过体绘制得到的沿射线r的累计权值之和。由式2,我们可以很容易地推导出$\begin{aligned}O\left(r\right)=\sum_{i=1}^{M}T_i\left(1-\exp\left(-\sigma_i\right)\right).\end{aligned}$。
C (r)和$\tilde{C}\left(r\right)$分别为查询射线的基于像素的渲染和gt的颜色,P (r)和$\tilde{P}\left(r\right)$分别为查询射线的基于patch的渲染和gt的颜色,$\mathcal{D}_{pix}$和$\mathcal{D}_{pat}$分别为渲染像素的颜色和渲染patch颜色的损失度量。经验上,我们选择$\mathcal{D}_{pix}$作为L1损失,$\mathcal{D}_{pat}$作为归一化互相关(NCC)损失。
这个公式背后的原理是,投影不一致的点总是有比较大的颜色误差,在优化中不能最小化。因此,如果在优化过程中颜色误差难以最小化,我们强制将累积权值$O (r)$的和设为零,这样在优化过程中就会排除不一致的区域。为了控制一致性水平,我们引入了两个逻辑正则化术语:λ0/λ1的比值越小,保留的区域越多;否则,更多的区域被排除,表面更干净。
Training loss
通过增强合成颜色和地面真值颜色的一致性,SparseNeuS的训练不依赖于三维地面真值形状。总损失函数定义为三个损失项的加权和:
$\mathcal{L}=\mathcal{L}_\mathrm{color~}+\alpha\mathcal{L}_\mathrm{eik}+\beta\mathcal{L}_\mathrm{sparse}.$
我们注意到,在通用训练的早期阶段,估计的几何形状相对不准确,并且3D表面点可能有很大的误差,其中误差不能提供关于区域是否亮度一致的明确线索。我们在每个场景的微调中利用了一致性感知的颜色损失,并在通用模型的训练中删除了Eq. 3$\mathcal{L}_\mathrm{color~}$的最后两个一致性感知逻辑项。
对采样点应用Eikonal项[9],对表面预测网络$f_θ$得到的SDF值进行正则化:
$\mathcal{L}_{eik}=\frac{1}{\left|\mathbb{Q}\right|}\sum_{q\in\mathbb{Q}}\left(\left|\nabla f_{\theta}\left(q\right)\right|_{2}-1\right)^{2},$
其中q为一个采样的三维点,$\mathbb{Q}$为所有采样点的集合,$\nabla f_{\theta}\left(q\right)$为网络$f_θ$相对于采样点q的梯度,$\left|\cdot\right|_{2}$为l2范数。Eikonal项强制网络$f_θ$具有单位l2范数梯度,这鼓励$f_θ$生成光滑的表面。
此外,由于体绘制中透光率的累积特性,可见面后面的不可见查询样本缺乏监督,导致可见面后面的自由面不可控。为了使我们的框架能够生成紧凑的几何曲面,我们采用稀疏正则化项来惩罚不可控的自由曲面:
$\mathcal{L}_{sparse}=\frac{1}{\left|\mathbb{Q}\right|}\sum_{q\in\mathbb{Q}}\exp\left(-\tau\cdot\left|s(q)\right|\right),$
其中$|s(q)|$为采样点q的绝对SDF值,τ为重新缩放SDF值的超参数。这一项将促使可见表面后面的点的SDF值远离0。在提取0级集SDF生成网格时,该项可以避免不可控的自由曲面。
Datasets and Implementation
Dataset
- DTU: like IDR scene
- 为了提高存储效率,我们使用分辨率为512 × 640的中心裁剪图像进行训练。我们观察到DTU数据集的图像包含大量的黑色背景,并且这些区域具有相当大的图像噪声,因此我们使用基于简单阈值的去噪策略来减轻训练图像中这些区域的噪声。可选地,RGB值为零的黑色背景可以用作简单的数据集,以鼓励这些区域的几何预测为空。
- BlendedMVS
- 我们在BlendedMVS[48]数据集的7个具有挑战性的场景上进行了进一步测试。对于每个场景,我们选择一组分辨率为768 × 576的三幅图像作为输入。请注意,在每个场景微调阶段,我们仍然使用这三张图像进行优化,而不使用任何新图像。
实现细节
使用特征金字塔网络[20]作为图像特征提取网络,从输入图像中提取多尺度特征。我们使用类似U-Net的架构实现了稀疏的3D CNN网络,并使用torchsparse[41]作为3D稀疏卷积的实现。粗级和精细级几何编码体的分辨率分别为96 × 96 × 96和192 × 192 × 192。基于补丁的混合中使用的补丁大小为5 × 5。
我们采用两阶段的训练策略来训练我们的通用模型:
- 第一阶段,首先训练粗级网络150k次迭代;
- 第二阶段,对精细级网络进行150k次迭代训练,对粗级网络进行固定训练。
我们在两个RTX 2080Ti gpu上训练我们的模型,批处理大小为512射线。
Experiments
我们将我们的方法与三种最先进的方法进行比较:
1)通用的神经渲染方法,包括PixelNerf [51], IBRNet[45]和MVSNerf[3],其中我们使用密度阈值从学习的隐式场中提取网格;
2)基于逐场景优化的神经表面重建方法,包括IDR[50]、NeuS[44]、VolSDF[49]、UniSurf [32];
3)广泛使用的经典MVS方法COLMAP[35],我们从COLMAP的输出点云中使用筛选泊松表面重建(filtered Poisson Surface Reconstruction)[16]重建网格。
所有方法都以三幅图像作为输入。
- Quantitative定量 comparisons.
- Qualitative comparisons.
- Ablations and analysis