Title	Challenging universal representation of deep models for 3D point cloud registration
Author	Bojani\’{c}, David and Bartol, Kristijan and Forest, Josep and Gumhold, Stefan and Petkovi\’{c}, Tomislav and Pribani\’{c}, Tomislav
Conf/Jour	BMVC
Year	2022
Project	DavidBoja/greedy-grid-search: [BMVC 2022 workshop] Greedy Grid Search: A 3D Registration Baseline (github.com)
Paper	Challenging the Universal Representation of Deep Models for 3D Point Cloud Registration (readpaper.com)

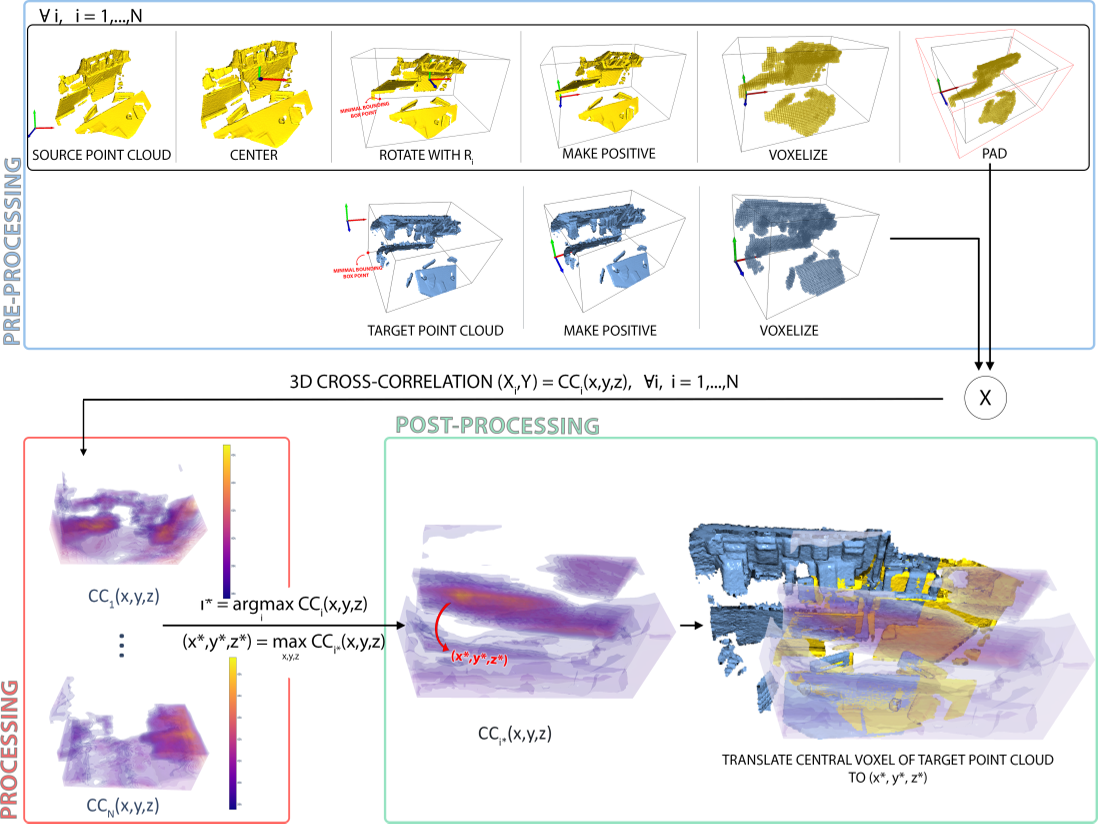
按步长穷举法，粗配准，需要根据ICP进行精配准

Abstract

学习跨不同应用领域的通用表示是一个开放的研究问题。事实上，在相同的应用程序中，在不同类型的数据集中找到通用的架构仍然是一个未解决的问题，特别是在涉及处理 3D 点云的应用程序中。在这项工作中，我们通过实验测试了几种最先进的基于学习的 3D 点云配准方法，以对抗所提出的非学习基线配准方法。所提出的方法优于或达到了基于学习方法的可比结果。此外，我们提出了一个基于学习的方法很难泛化的数据集。我们提出的方法和数据集，以及提供的实验，可以用于进一步研究通用表示的有效解决方案

比较好的泛化
提出了新基准 FAUST-partial，基于 3D 人体扫描，这进一步对基于学习的方法的泛化提出了挑战
提出了一种新的三维配准基线，该基线根据体素化点云之间的最大相互关系选择变换候选点
在公共基准测试中展示与最先进的 3D 配准方法相当的性能，并在 FAUST-partial 上优于它们

Method

分为三步：

Pre-Processing
- 源点云X居中并按一定的 step 旋转(预计算N个旋转矩阵)，得到 N 个旋转后的源点云，然后将源点云移动到坐标全为正值的象限(方便体素化)，然后将 N 个源点云和目标点云Y体素化(voxel resolution of VR cm)，没有使用 0 1 值的 3D 网格，而是为体素填充正值 PV(包含点云点)和负值 NV( 不包含点云点)
- 得到 N 个 source volumes 和 1 个 target volume
Processing
- 计算每个 source volume 与 target volume 的 3D cross-correlation(两个 volume 的体素值相乘并相加)，结果产生 N 个 cross-correlation volumes 与 source volumes 的三个维度相同，可以使用 heatmaps 表示匹配度的高低。
- cross-correlation 之前，每个 source volume 应该被 pad 以便 target volume 在 source volume 上 slide，用 6 维的 P 表示 Pad，每个维度分别表示在 source volume 的左右上下前后 pad 的数量
- 使用 Fourier 加速 cross-correlation 的计算，首先将两个 volume 使用 FFT 转换到 Fourier space，将 cross-correlation 简化为矩阵乘法，然后使用逆 FFT 将输出转换回来
Post-Processing
- 使用预先计算的旋转矩阵中的一个来估计将X旋转到Y的旋转矩阵(CC最大的source volume)
- 同时将target volume 的中心移动到最大CC volume voxel (xyz)，由于最大CC volume相对应某个source volume，本质上是将target volume 体素中心移动到 source volume 体素中心(使得CC最大)

$\left(\hat{R}\left(\mathcal{X}-t_{\mathcal{X}}^{\text{CENTER}}\right)\right)+t_{\mathcal{X}}^{\text{POSIT}}\sim\left(\mathcal{Y}+t_{\mathcal{Y}}^{\text{POSIT}}\right)-t_{\text{est}}$
其中~表示左右部分是对齐的，X源点云和Y目标点云，$t_{\mathcal{X}}^{\text{CENTER}}$将源点云的质心移动到原点，$t^{\text{POSIT}}$将最小边界框点移动到原点

公式变形：
$\left(\hat{R}\left({\mathcal X}-t_{\mathcal X}^{\mathrm{CENTER}}\right)\right)+t_{\mathcal X}^{\mathrm{POSIT}}+t_{\mathrm{est}}-t_{\mathcal Y}^{\mathrm{POSIT}}\sim{\mathcal Y}$
$\hat{R}=R_{i^{*}},\quad\hat{t}=-\hat{R}t_{\mathcal{X}}^{\mathrm{CENTER}}+t_{\mathcal{X}}^{\mathrm{POSIT}}+t_{\mathrm{est}}-t_{\mathcal{Y}}^{\mathrm{POSIT}}$

Refinement:
由于旋转和平移空间是离散的，所以初始对齐只是一个粗略的估计。如果地面真值解位于估计的离散位置，则旋转和平移误差的上界为$\frac12\max_{i,ji\neq j}\arccos\left(\frac{\operatorname{trace}(R_i^TR_j)-1}2\right)\frac{180}\pi$ degree 和$\frac{\mathrm{VR}\sqrt{3}}{2}$ cm。对于S = 15◦和V R = 6cm的角度步长，上限误差为7.5◦和5cm。因此，粗略的初始对齐应该为精细的配准算法提供非常好的初始化。我们使用广义ICP[53]来refine初始解决方案，因为它提供了最好的结果

Conclusion

提出的经典方法提供了良好的三维配准基线。该方法简单有效，并在公共基准测试中得到了验证。与最先进的方法的泛化性能相比，基线是相同的。在新提出的FAUST-partial基准测试中，即使生成的云对之间的重叠相当高，竞争方法也难以保留结果，或者执行得更差。与深度学习方法相反，基线简单且可解释，可用于详细分析。不同策略的效果是清晰和直观的，并提供了对注册过程的见解。因此，在寻找通用表示的过程中，设计一个模仿所提出的基线方法的深度模型是一个有趣的未来发展方向。