| Title | Sources of Uncertainty in 3D Scene Reconstruction |
|---|---|
| Author | Marcus Klasson and Riccardo Mereu and Juho Kannala and Arno Solin |
| Conf/Jour | ECCV Workshop on Uncertainty Quantification for Computer Vision. |
| Year | 2024 |
| Project | AaltoML/uncertainty-nerf-gs: Code release for the paper “Sources of Uncertainty in 3D Scene Reconstruction” |
| Paper | Sources of Uncertainty in 3D Scene Reconstruction |
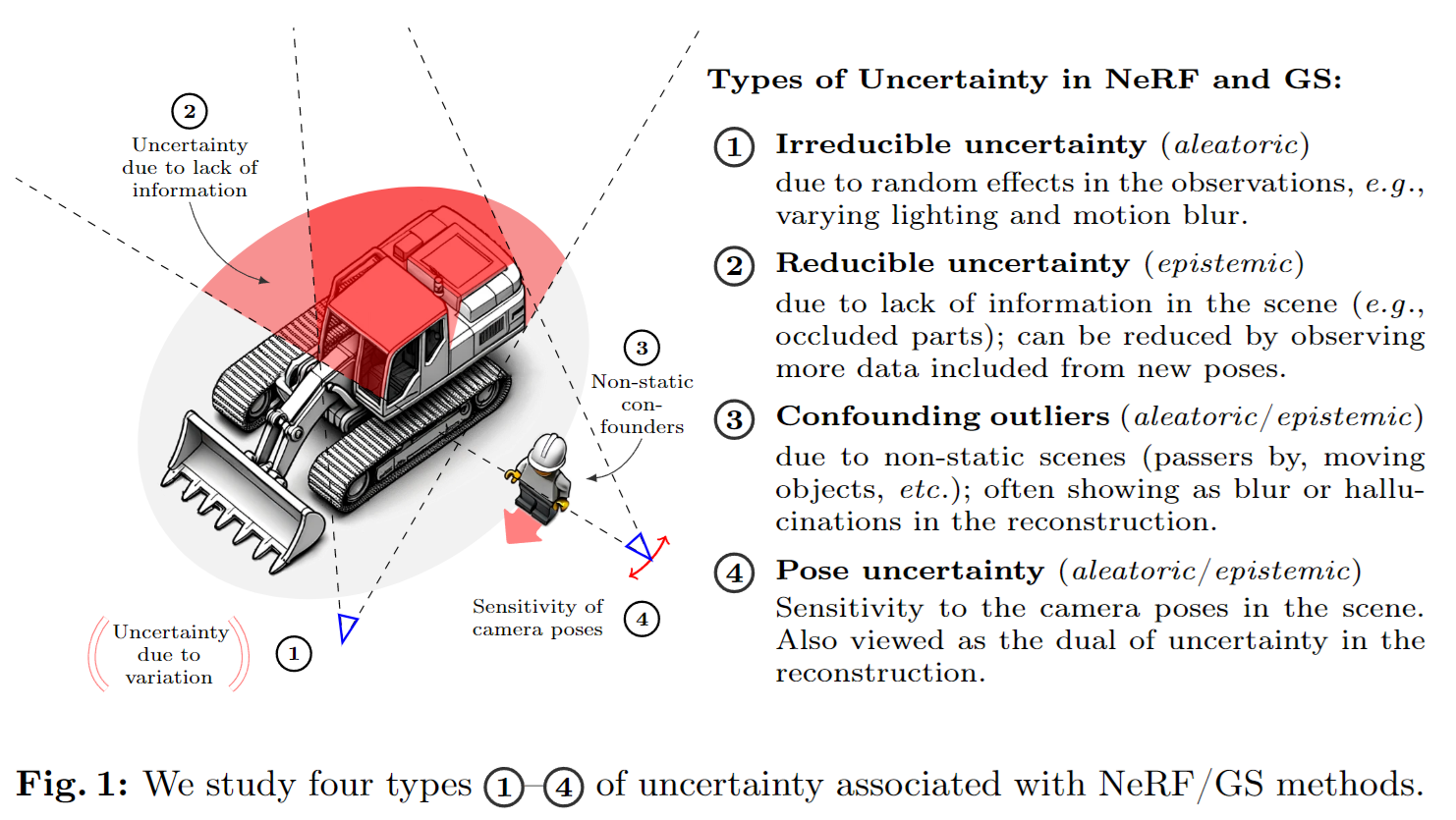
Q: 环境光照可以建模为不确定性吗?
AIR
- Aleatoric Uncertainty
- random effects in the observations include varying lighting and motion blur
- Epistemic Uncertainty
- lack of information in the scene such as occluded (can be reduced by observing more data from new poses)
- challenging scenes : low texture, repetitive patterns and insufficient overlap in images
- Confounding outliers
- non-static scenes (passers by, moving object)
- non-static elements in a scene, such as moving people or vegetation, introduce variability that is often interpreted as aleatoric noise. However, these elements can also obscure parts of the scene, acting as a source
of occlusion for parts of the scene
- non-static elements in a scene, such as moving people or vegetation, introduce variability that is often interpreted as aleatoric noise. However, these elements can also obscure parts of the scene, acting as a source
- non-static scenes (passers by, moving object)
- Pose Uncertainty
- Sensitivity to the camera poses in the scene
Contribution:
- identify and categorize sources of uncertainties in 3D scene reconstruction and propose methods for systematically evaluating their impact.
- perform an empirical study using efficient NeRF and GS models from Nerfstudio [49] to compare the performance of various uncertainty estimation techniques on the sources of uncertainty.
RelatedWork:
- Uncertainty Estimation in Deep Learning:
- Aleatoric Uncertainty commonly is modeled to predict a Probability Distribution from the network (mean and variance). However, this modification is insufficient to model epistemic uncertainty in the model parameters,
- Epistemic Uncertainty
- Bayesian deep learning methods give means to quantify epistemic uncertainty through posterior approximations to obtain the predictive distribution.
- nsembles estimate uncertainty by predictions from multiple networks trained with different weight initializations
- MC-Dropout performs predictions by masking weights in the network by enabling dropout at test time.
- the Laplace approximation has been shown to be a scalable and fast option to obtain predictive uncertainties from already-trained networks in a post-hoc fashion
- Uncertainty Estimation in NeRFs and GS
- ActiveNeRF models a Gaussian distribution over rendered RGB pixels with the goal of next-best view selection, which spurred interest in this application as well as exploring more flexible probability distributions.
- Estimating epistemic uncertainty in few-view settings was studied, which require significant modifications to the NeRF architecture as they use variational inference for optimization.
- Later works have focused on architecture agnostic不可知论 approaches, used ensembles of efficient NeRF backbones to estimate uncertaintie
- a calibration method for correcting uncalibrated predictions on novel scenes of already-trained NeRFs
- Bayes’ Rays uses perturbations in a spatial grid to define a NeRF architecture-agnostic spatial uncertainty estimated using the Laplace approximation,
- while FisherRF [14] computes the Fisher information over the parameters in both NeRF- and GS-based methods to quantify the uncertainty of novel views.
- Recently, robustness to confounding outliers and removing distractors has been studied
- using view-specific embeddings
- leveraging pre-trained networks
- using robust optimization to learn what scene parts are static and dynamic
- Other works have aimed to consider aleatoric noise, motion blur and rolling shutter effects, by explicitly modeling for these
- Furthermore, camera pose optimizers have been proposed to correct inaccurate camera parameters alongside optimizing the scen
Method
In particular, for the aleatoric ones, we adapt the approach proposed in Active-NeRF [30], while, for the epistemic approaches, we use MC-Dropout [7], the Laplace approximations [6] and ensembles [19].
- ActiveNeRF: Learning where to see with uncertainty estimation.
- Dropout as a Bayesian approximation: Representing model uncertainty in deep learning.
- Laplace redux-effortless Bayesian deep learning.
- Simple and scalable predictive uncertainty estimation using deep ensembles.
limit the use of MC-Dropout and LA to NeRFs since both are Bayesian deep learning methods and, thus, non-trivial to extend to GS. 两个都是通过预测一条光线上的点颜色(NeRF连续),无法简单的用到3DGS中*,两外两个Active-NeRF 和 Ensemble 可以用是因为他们用不同的trained 网络来建模不确定性
Active-NeRF/GS
颜色被处理成gaussian random variable $\mathbf{c}\sim\mathcal{N}(\mathbf{c};\bar{\mathbf{c}},\beta)$ $\bar{\mathbf{c}}\in\mathbb{R}^3$,$\beta\in\mathbb{R}^+$ 并学习均值和方差,方差由另一个网络进行预测
方差被表述为单个量,没有考虑不同通道的color方差不同
$\mathbf{c}_{\text{Active-NeRF}}=\sum_{i=1}^{N_s}T_i\alpha_i\bar{\mathbf{c}}_i\quad\mathrm{and}\quad\mathrm{Var}(\mathbf{c}_{\text{Active-NeRF}})=\sum_{i=1}^{N_s}T_i^2\alpha_i^2\beta_i,$
$\mathbf{c}_{\text{Active-GS}}=\sum_{i=1}^{N_p}T_i\alpha_i\bar{\mathbf{c}}_i\mathrm{~and~}\mathrm{~Var}(\mathbf{c}_{\text{Active-GS}})=\sum_{i=1}^{N_p}T_i\alpha_i\beta_i,$
MC-Dropout NeRF
The uncertainty is estimated by applying dropout M times during inference to obtain M rendered RGB predictions,然后计算这M个rendered color的均值与方差
均值就是均匀分布的期望
这里方差公式应该是写错了吧,应该是:$\mathrm{Var}(\mathbf{c}_{\mathrm{MC-Dropout}}) \approx\frac1M\sum_{m=1}^M\mathbf{c}_{\text{NeRF}}^2-\left(\frac1M\sum_{m=1}^M\mathbf{c}_{\text{NeRF}}\right)^2.$
Laplace NeRF
The idea is to approximate the intractable posterior distribution over the weights with a Gaussian distribution centered around the mode of $p(\mathbf{\theta|\mathcal{D}})$, where $\mathcal{D}$ is the training data set.
- Mean is set as a local maximum of the posterior $\mathbf{\theta^{*}}=\arg\max_{\mathbf{\theta}}\log p(\mathbf{\theta|\mathcal{D}})$ is obtained by training the network until convergence.
- Covariance matrix $\log h(\mathbf{\theta})\approx \log h\left( \mathbf{\theta^{}}-\frac{1}{2}(\mathbf{\theta}-\mathbf{\theta^{}})^{\top}\mathrm{H}(\mathbf{\theta}-\mathbf{\theta^{*}}) \right)$
- by Taylor expanding $\log p(\mathbf{\theta}|\mathcal{D})$ around $\mathbf{\theta^{*}}$
- $\mathrm{H}=-\nabla^{2}_{\mathbf{\theta}\log h(\mathbf{\theta})|_{\mathbf{\theta^{}}}}$ is the Hessian matrix of the unnormalized log-posterior at $\mathbf{\theta^{}}$
the Laplace posterior approximation as the Gaussian distribution $p(\boldsymbol{\theta}\mid\mathcal{D}) \approx q(\boldsymbol{\theta}) = \mathcal{N}(\boldsymbol{\theta}\mid\boldsymbol{\theta}^*,\mathbf{H}^{-1})$
pointcloud color mean $\hat{\mathbf{c}}$ and variance $\hat{\beta}$ for every input $\mathbf{x}$ along the ray via MC sampling from approximate posterior
$\mathbf{c}_{\text{Laplace}}=\sum_{i=1}^{N_s}T_i\alpha_i\hat{\mathbf{c}}_i\quad\text{and}\quad\text{Var}(\mathbf{c}_{\text{Laplace}})=\sum_{i=1}^{N_s}T_i^2\alpha_i^2\hat{\beta}_i.$
Ensemble NeRF/GS
training M network with different weight initialization to different local minima
$\mathbf{c}_{\mathrm{ens}}=\frac1M\sum_{m=1}^M\mathbf{c}_{\mathrm{NeRF/GS}}^{(m)}\text{ and Var}(\mathbf{c}_{\mathrm{ens}})\approx\frac1M\sum_{m=1}^M\mathbf{c}_{\mathrm{ens}}^2-\left(\frac1M\sum_{m=1}^M\mathbf{c}_{\mathrm{ens}}\right)^2.$
同理这里方差公式也写错了,应该是:$\text{Var}(\mathbf{c}_{\mathrm{ens}})\approx\frac1M\sum_{m=1}^M\mathbf{c}_{\mathrm{NeRF/GS}}^2-\left(\frac1M\sum_{m=1}^M\mathbf{c}_{\mathrm{NeRF/GS}}\right)^2.$
Experiments
aleatory:不可减少的随机不确定性
epistemic:可减少的认知不确定性
① a 观察时的随机影响,例如光照变化,或运动模糊
② e 缺少场景的信息,如图片数量不足
③ a+e 非静态场景,例如行人或移动的物体,导致重建模糊/幻觉
④ a+e 相机位姿的敏感性
Datasets:
- Mip-NeRF 360 and Blender datasets for ① and ②
- Light Field (LF) data set and follow the few-shot setting for ②
- RobustNeRF and On-the-go data sets to evaluate robustness against confounding objects in the training views for ③
- Mip-NeRF 360 data set for ④
Metrics:
- 图片质量:PSNR、SSIM、LPIPS
- 不确定性估计:negative log likelihood (NLL)
- Area Under Sparsification Error (AUSE) 不确定性与预测误差之间的相关程度
- Area Under Calibration Error (AUCE) to assess the calibration of each method
| Experiments | Datasets | Trainsets | Testsets |
|---|---|---|---|
| ① | Mip-NeRF 360 (1.0~1.6 megapixels) | Gaussian noise or Gaussian blur | without noise |
| ② | Mip-NeRF 360 | randomly sample 10%, 25%, 50%, and 100% | regularly subsample 10% |
| Mip-NeRF 360 | 一个方向的视图 | 另一个方向的视图 | |
| LF data set | few-view setting | ||
| ③ | RobustNeRF and On-the-go data set | 非静态物体,导致渲染照片出现漂浮物 | |
| RobustNeRF | different clutter proportions | ||
| On-the-go | different occlusion levels | ||
| ④ |
① sensitivity under different confounding effects applied to the training images
② (i) sensitivity to the number of training views;
(ii) sensitivity to views that are different from the training views (out-of-distribution, OOD);
OOD setting:separate the training and test sets by splitting all input images based on their camera pose positions

(iii) sensitivity to few views with limited scene coverage.
③ the sensitivity of each method to learning from cluttered(凌乱的) training views. (非静态物体,可以是玩具/人)
④ the sensitivity (uncertainty) aspect of imprecise camera poses in 3D scene reconstruction
使用颜色对相机位姿的梯度来量化敏感性 $\partial\mathbf{c}/\partial\mathbf{P}\in\mathbb{R}^{3\times4},$沿着z轴随机移动相机位置作为扰动,扰动足够小使得可以在扰动和非扰动gradient normal maps之间进行像素级的比较