QiYun

Note

Structured Light Review

Posted on Edited on In
3.9k 14 mins.

结构光三维重建

参考：
结构光综述 - 知乎 (zhihu.com)

结构光原理

结构光主要可以分为两类

  1. 线扫描结构光；线扫描结构光较之面阵结构光较为简单，精度也比较高，在工业中广泛用于物体体积测量、三维成像等领域。
  2. 面阵结构光；

线扫描结构光

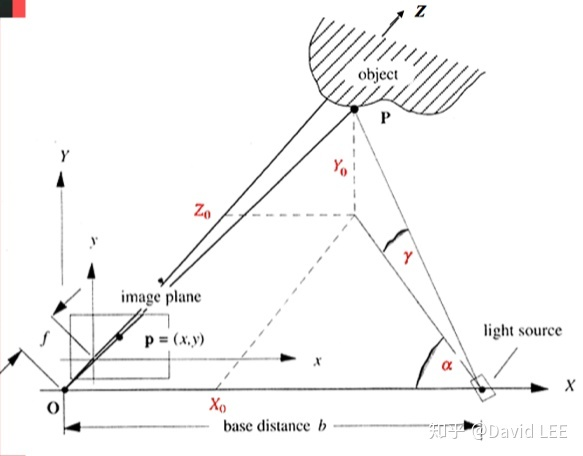
image.png|666

由小孔成像模型有 $\frac Xx=\frac Zf=\frac Yy$
由三角测量原理又有 $\tan\alpha=\frac Z{b-X}$
两式联立则有
$\begin{aligned}&Z=\frac Xx\cdot f=\tan\alpha\cdot(b-X)\\&X\cdot(\frac fx+\tan\alpha)=\tan\alpha\cdot b\end{aligned}$

可得，所测物体点的三维坐标与俯仰角 $\gamma$ 无关
$\begin{aligned}X&=\frac{\tan\alpha\cdot b\cdot x}{f+x\cdot\tan\alpha}\\Y&=\frac{\tan\alpha\cdot b\cdot y}{f+x\cdot\tan\alpha}\\Z&=\frac{\tan\alpha\cdot b\cdot f}{f+x\cdot\tan\alpha}\end{aligned}$

面阵结构光

面阵结构光大致可以分为两类：随机结构光和编码结构光。

  • 随机结构光较为简单，也更加常用。通过投影器向被测空间中投射亮度不均和随机分布的点状结构光，通过双目相机成像，所得的双目影像经过极线校正后再进行双目稠密匹配，即可重建出对应的深度图。如下图为某种面阵的红外结构光。(和普通双目算法很相似)
  • 编码结构光可分为：
    • 时序编码：高精度，但只适用于静态场景且需要拍摄大量影像
    • 空间编码：无需多张照片，只需要一对影像即可进行三维重建。可以满足实时处理，用在动态环境中，但易受噪声干扰：由于反光、照明等原因可能导致成像时部分区域等编码信息缺失；对于空间中的遮挡比较敏感；相较于时序编码结构光精度较低

时序编码结构光
在一定时间范围内，通过投影器向被测空间投射一系列明暗不同的结构光，每次投影都通过相机进行成像。则通过查找具有相同编码值的像素，来进行双目匹配

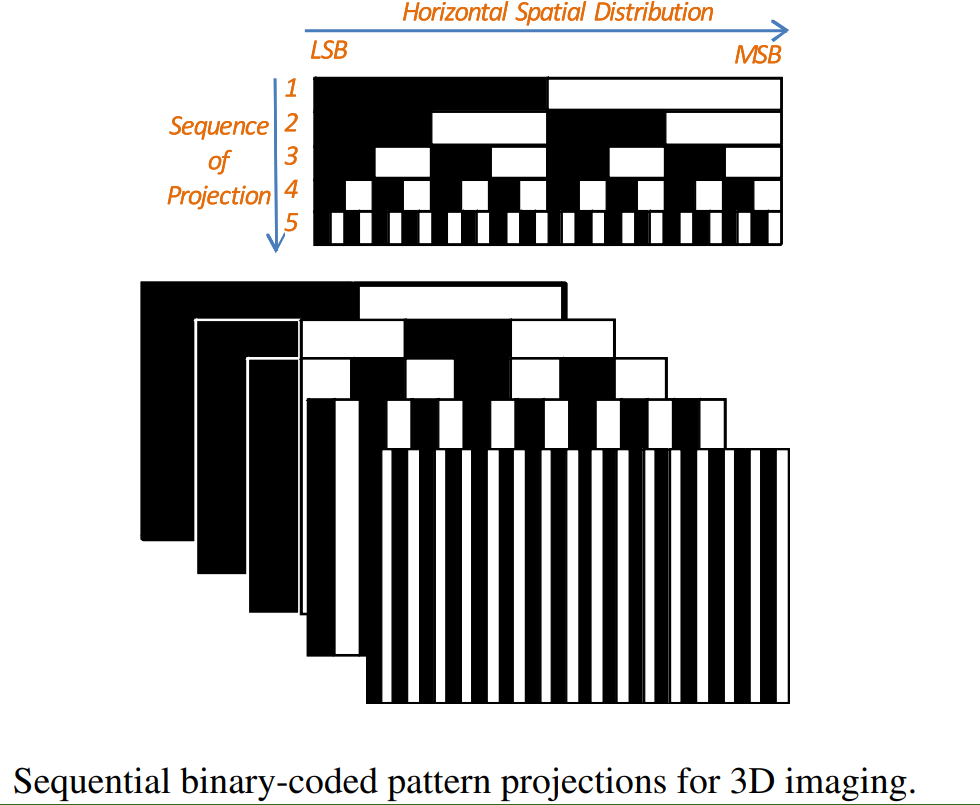
image.png|666

空间编码结构光
为满足动态场景的需要，可以采用空间编码结构光。空间编码结构光特指向被测空间中投影经过数学编码的、一定范围内的光斑不具备重复性的结构光。由此，某个点的编码值可以通过其临域获得。其中，包含一个完整的空间编码的像素数量（窗口大小）就决定了重建的精度

De Bruijn sequence

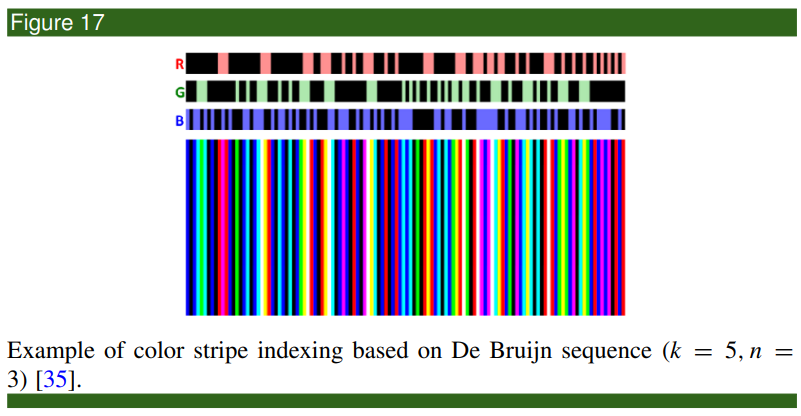
image.png|666

2D Spatial Grid Patterns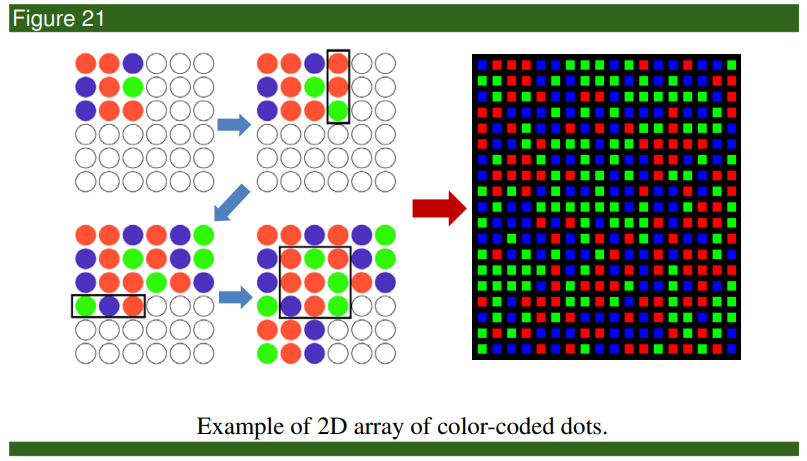
image.png|666

结构光三维重建项目

几个 Github 项目：

FourStepPhaseShifting

jiayuzhang128/FourStepPhaseShifting

使用”互补格雷码+相移码”方法获取被测物体的三维信息
相机标定获得相机内外参

硬件设备搭建

  • DLP 投影仪：闻亭 PRO6500
  • 灰度相机：FLIR BFS-U3-50S5
  • 旋转平台

image.png|666

投影仪-相机系统标定

投影仪-相机系统标定方法_投影仪标定-CSDN博客
Projector-Camera Calibration / 3D Scanning Software (brown.edu)

一般相机标定

—>得到精确的相机内外参和畸变参数
张正友标定法-完整学习笔记-从原理到实战 - 知乎 (zhihu.com)

  • 相机标定的目的是：建立相机成像几何模型并矫正透镜畸变
    • 建立物体从三维世界映射到相机成像平面这一过程中的几何模型非常重要，而这一过程最关键的部分就是要得到相机的内参和外参
    • 由于小孔成像只有小孔部分能透过光线就会导致物体的成像亮度很低，因此发明了透镜，但由于透镜的制造工艺，会使成像产生多种形式的畸变

透镜的畸变主要分为径向畸变和切向畸变，我们一共需要 5 个 3 个畸变参数（k1、k2、k3、p1 和 p2 ）来描述透镜畸变

  • 径向畸变是由于透镜形状的制造工艺导致。且越向透镜边缘移动径向畸变越严重
  • 切向畸变是由于透镜和 CMOS 或者 CCD 的安装位置误差导致。因此，如果存在切向畸变，一个矩形被投影到成像平面上时，很可能会变成一个梯形

标定过程：固定相机，改变棋盘标定板的位姿，一般拍摄 20 组以上照片

  • 根据两张图片中棋盘特征点的世界坐标位置和像素坐标位置，可以得到单应性矩阵(特征点从一张图片变换到另一张图片的变换矩阵，单应性矩阵H 是内参矩阵和外参矩阵的混合体)
  • 先不考虑镜头畸变，根据旋转向量之间的两个约束关系和单应性矩阵，得到相机的内参
    • 如果图片数量 n>=3，就可以得到唯一解 b(相机内参)
  • 上述只是理论过程，在实际标定过程中，一般使用最大似然估计进行优化

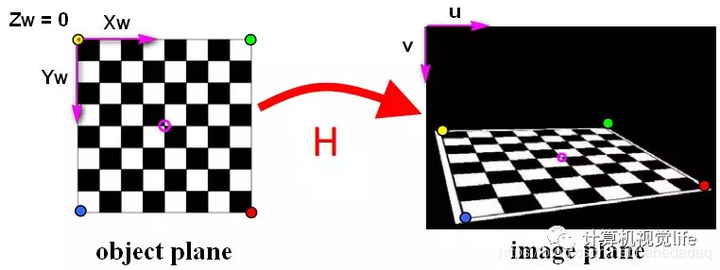
image.png|666

标定实战
MATLAB 自带相机标定应用程序，有 camera calibrator 和 stereo camera calibrator 两类相机标定应用程序。其操作简单、直观，能够获得相机的内、外参数以及畸变参数等

投影仪-相机系统标定

Projector-Camera Calibration / 3D Scanning Software (brown.edu)

用带有径向和切向畸变的小孔模型描述相机和投影仪 相机模型

基于相移法的结构光三维重建

互补格雷码+相移码 FourStepPhaseShifting/support/原理介绍.pdf or CSDN1 + CSDN2

相移法的结构光通过投影仪投射一系列正弦编码的条纹图案到被测物体表面，然后通过相机采集发生形变的条纹图像，继而根据相移算法进行解码获得待测物体表面的深度信息

image.png|666

生成四步相移图像

N 步相移码：首先相移码的原理是利用 N 幅正弦条纹图通过投影仪投射到物体表面再通过相机拍摄获取图像，通过所得图像计算每个位置的相位差，然后通过相位—深度的映射关系获取物体的深度信息。

投影光栅的光强函数
$\begin{aligned}&I_n(x,y)=A(x,y)+B(x,y)cos[\varphi(x,y)+\Delta\varphi_n]\\{}\\&\Delta\varphi_n=2\pi(n-1)/N(n\in[1,N])\end{aligned}$

  • A(x,y)表示背景光强，B(x,y)表示调制幅值
  • $\varphi(x,y)$ 表示包裹相位（相对相位）
  • $\Delta\varphi_n$ 表示平移相位

由于选用 4 位格雷码+四步相移，编码区域可以分为 16，因此相移码的周期数，周期 $T=Width/f$
$\varphi(x,y)=\frac{2\pi fx}{Width}$ Width 表示图像宽度(单位:像素)

相移条纹图(下)生成公式，$u_p,v_p$ 表示投影仪像素坐标；T 表示单根条纹在一个周期内的像素数量
$\begin{gathered}\begin{aligned}&I_0(u_p,\nu_p)=0.5+0.5\cos(2\pi\frac{u_p}T) \\&I_{1}(u_{p},\nu_{p})=0.5+0.5\cos(2\pi\frac{u_{p}}{T}+\frac{\pi}{2}) \\&I_2(u_p,\nu_p)=0.5+0.5\cos(2\pi\frac{u_p}T+\pi) \\&I_{3}(u_{p},\nu_{p})=0.5+0.5\cos(2\pi\frac{u_{p}}{T}+\frac{3\pi}{2})\end{aligned} \end{gathered}$

代码生成：

  • 第一步：生成一个 1920 维的行向量；
  • 第二步：利用公式 $I(x,y)=128+127cos[2\pi(\frac{fx}{Width}+\frac{n-1}N)]$ 对每一个向量元素进行填充；
  • 第三步：利用 np.Tile() 函数生成 1080 行，得到 1920*1080 的矩阵；
  • 第四步：利用 cv2.imshow() 函数显示。

格雷码(中)

一种二进制码制，是一种无权码，它的特点是前后相邻码值只改变一位数，这样可以减小错位误差，因此又称为最小错位误差码。

十进制数 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
格雷码 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000

生成 n 位格雷码:

  • 传统方法
    • 第一步，生成 n 位全零码
    • 第二步，改变最右端的码值
    • 第三步，改变自右起第一个“1”码元左边的码元
    • 重复第二、三步直至得到 2^n 个格雷码
  • 递归法：n 位格雷码可以由（n-1）位格雷码得到
    • 第一步：（n-1）位格雷码正序排列最左侧（前缀）补 0
    • 第二步：（n-1）位格雷码逆序排列最左侧（前缀）补 1
    • 第三步：一、二步得到结果依次排列得到 n 位格雷码
1
2
3
4
5
6
7
8
9
10
11
12
递归法：
1位：0 1 
正序 00 01 
逆序 11 10 
2位：00 01 11 10 
正序 000 001 011 010 
逆序 110 111 101 100 
3位：000 001 011 010 110 111 101 100
正序 0000 0001 0011 0010 0110 0111 0101 0100
逆序 1100 1101 1111 1110 1010 1011 1001 1000
4位：0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000
...

格雷码与普通二进制码的转换

  • 传统方法：
    • 二进制码—>格雷码：二进制码与其右移一位高位补零后的数码异或后得到格雷码
    • 格雷码—>二进制码：最左边的一位不变，从左边第二位起，将每位与左边一位解码后的值异或，作为该位解码后的值。依次异或，直到最低位。依次异或转换后的值（二进制数）就是格雷码转换后二进制码的值

在生成格雷码的同时，将每一位格雷码与其对应的十进制数组成键值对储存在字典中，这样在进行二进制码、格雷码、十进制相互转换时可以直接查询字典完成比较方便
本项目采用的互补格雷码，需要 4 位格雷码图和 5 位格雷码的最后一张，详细代码可以查看 python 版本代码。

投影获得图像

image.png|666

求解相对相位(包裹相位)

数字条纹投影~标准N步相移主值相位计算式推导过程_up六月上的博客-CSDN博客

$\begin{aligned}I_2(u_c,\nu_c)-I_0(u_c,\nu_c)=&0.5\left(\cos[\phi(u_c,\nu_c)+\pi]-\cos[\phi(u_c,\nu_c)]\right)=-\cos[\phi(u_c,\nu_c)]\\I_3(u_c,\nu_c)-I_1(u_c,\nu_c)=&0.5\left\{\cos\left[\phi(u_c,\nu_c)+\frac{3\pi}2\right]-\cos\left[\phi(u_c,\nu_c)+\frac\pi2\right]\right\}=\sin[\phi(u_c,\nu_c)]\end{aligned}$

$\phi(u_c,\nu_c)=-\arctan\frac{I_3(u_c,\nu_c)-I_1(u_c,\nu_c)}{I_2(u_c,v_c)-I_0(u_c,\nu_c)},\phi(u_c,\nu_c)\in\left[-\pi,\pi\right]$
$𝑢_𝑐$、$𝑣_𝑐$ 表示相机获取图像的像素标, $\phi(u_c, v_c)$ 表示该像素点的包裹相位

将每一个像素利用上述方法求得包裹相位并储存在对应位置，可以得到所有对应位置的数值大小都在 $[0,2\pi]$,然后对其进行线性放缩到 $[0,255]$

image.png|666

求绝对相位

相位展开获得绝对相位(得到了投影仪像素坐标与相机像素坐标的关系)
GC 表示格雷码图，k1、k2 表示对应的编码值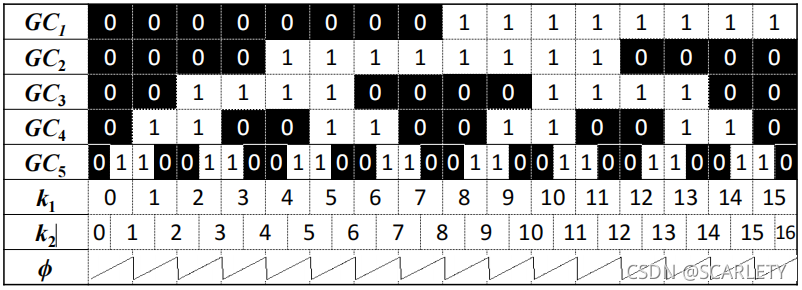
image.png|666

包裹相位ϕ如上图，要想将上面的包裹相位还原成连续的绝对相位，只要在每一个截断处加上2kπ(k 表示周期的级次),就可以恢复成连续的相位。($\phi(x,y) = \varphi(x,y) + 2 \pi k_1(x,y)$)因此我们用四幅格雷码图像将整个有效视区分成 16 份并分别编码，因此这里的周期级次 K 就等于格雷码的编码值（k1），但是由于实际过程中，由于投影仪和相机的畸变效应，所投的格雷码图像与相移码图像会产生错位：
由于错位发生在包裹相位的截断处，为了解决错位问题，我们引入一张5位格雷码，与4位格雷码形成互补，k2的计算公式：$K2=INT[(V2+1)/2]$，INT:向下取整，V2：GC0-GC5 格雷码对应的十进制数。

利用以下公式就可以避免截断处产生错位：
$\phi(x,y)=\begin{cases}\varphi(x,y)+2\pi k_2(x,y),~\varphi(x,y)\leq\frac\pi2\\\\\varphi(x,y)+2\pi k_1(x,y),~\frac\pi2<\varphi(x,y)<\frac{3\pi}2\\\\\varphi(x,y)+2\pi[k_2(x,y)-1],~\varphi(x,y)\geq\frac{3\pi}2&\end{cases}$

在相机实际拍摄的图片中由于环境光的影响，拍摄到的格雷码值并不是标准的二值图，需要二值化:

  • 首先要将格雷码图像进行二值化处理
  • 然后计算 k1、k2 的值
  • 最后带入公式求解绝对相位 $\phi(x,y)$

image.png|666

然后求解三维坐标，获得三维点云(根据各坐标系的关系以及相机和投影仪的参数)

获得相机-投影仪像素坐标之间的对应关系

由相机像素坐标 $u_c,v_c$，投影仪像素坐标 $(u_p,v_p)$

$\Phi(\operatorname{u_P},\operatorname{v_P})=\Phi(\operatorname{u_C},\operatorname{v_C})$
$\Phi(\operatorname{u_P},\operatorname{v_P})=\frac{2\pi\operatorname{u_p}}{\operatorname{T}}$

可得：

根据标定参数获得重建点云信息

由相机内外参矩阵，可以得到像素坐标与世界坐标之间的关系：

$x_c,y_c$ 为 $u_c,v_c$ 的相机坐标，世界坐标 $X_w,Y_w,Z_w$ 旋转平移得到 $X_c,Y_c,Z_c$

同理投影仪：

由相机和投影仪外参关系：

可得：

由相机投影仪像素坐标关系：

联立上述两式：

可得：$Z_{c}=\frac{x_{p}t_{z}-t_{x}}{J_{x}-J_{z}x_{p}}$

其中

则相机坐标系下，每个像素的世界坐标为：

Welcome to my other publishing channels