QiYun

Note

DMTet

Posted on Edited on In
2.8k 10 mins.
Title Deep Marching Tetrahedra: a Hybrid Representation for High-Resolution 3D Shape Synthesis
Author Tianchang Shen and Jun Gao and Kangxue Yin and Ming-Yu Liu and Sanja Fidler
Conf/Jour NeurIPS
Year 2021
Project Deep Marching Tetrahedra: a Hybrid Representation for High-Resolution 3D Shape Synthesis (nvidia.com)
Paper Deep Marching Tetrahedra: a Hybrid Representation for High-Resolution 3D Shape Synthesis (readpaper.com)

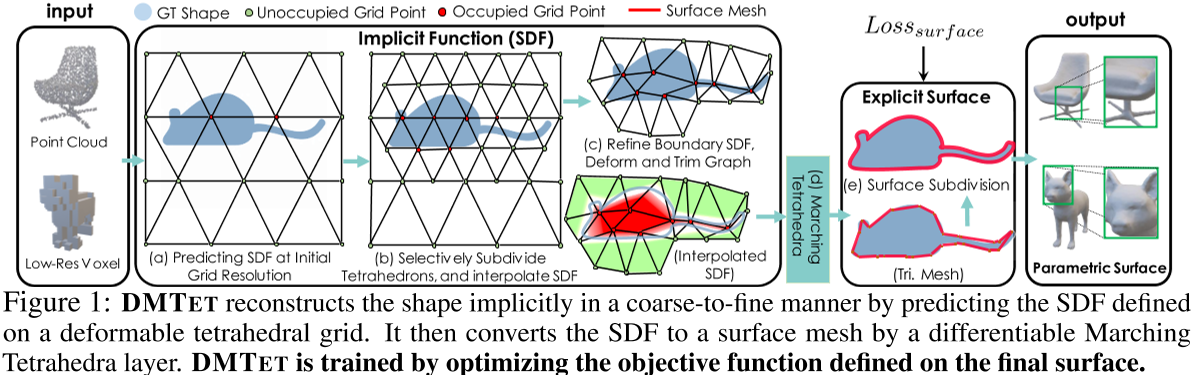
image.png|666

输入点云或低分辨率体素，提取特征后利用GAN网络，生成每个顶点的位置和SDF偏移值，得到优化后顶点的位置和SDF
结合显式与隐式表达的表示方法，利用MT，从隐式SDF中重建出显式mesh

Abstract

我们介绍了 DMTET，一个深度3D 条件生成模型，可以使用简单的用户指南(如粗体素)合成高分辨率3D 形状。它通过利用一种新的混合3D 表示结合了隐式和显式3D 表示的优点。与目前的隐式方法相比，DMTET 直接针对重建表面进行优化，使我们能够以更少的人工合成更精细的几何细节。与直接生成显式表示(如网格)的深度3D 生成模型不同，我们的模型可以合成具有任意拓扑结构的形状。DMTET 的核心包括一个可变形的四面体网格，它编码一个离散的符号距离函数和一个可微的移动四面体层，它将隐式的符号距离表示转换为显式的表面网格表示。这种组合允许表面几何和拓扑结构的联合优化，以及使用重建和在表面网格上明确定义的对抗损失来生成细分层次。我们的方法明显优于现有的粗糙体素输入条件形状合成的工作，这些工作是在复杂的3D 动物形状数据集上训练的。项目页面: https://nv-tlabs.github.io/DMTet/

贡献：

  • 我们表明，与之前的研究[31,45]的分析相比，使用行进四面体(MT)作为可微的等面层允许隐式场表示的底层形状的拓扑变化。
  • 我们将 MT 合并到深度学习框架中，并引入 DMTET，这是一种结合隐式和显式表面表示的混合表示。我们证明了直接在从隐场提取的表面上定义的额外监督(例如倒角距离，对抗损失)提高了形状合成质量。
  • 我们引入了一种从粗到精的优化策略，在训练期间将 DMTET 扩展到高分辨率。因此，在具有挑战性的三维形状合成任务中，我们比最先进的方法获得了更好的重建质量，同时需要更低的计算成本。

Method

3D Representation

image.png|666

  • 采用 DefTet：不同于 DefTet 用占用值表示, 本文用 SDF 表示 shape, SDF 由可变形的四面体网格编码
  • 与八叉树思想类似，围绕预测表面细分四面体
  • 使用 Marching Tetrahedra layer 将从 SDF 的隐式表示中提取三角形 mesh

Deformable Tetrahedral Mesh as an Approximation of an Implicit Function

将四面体表示为 $(V_T,T)$，$V_{T}$ 表示 4 个顶点 $\{v_{ak} , v_{bk} , v_{ck} , v_{dk}\}$，共有 T 个四面体
通过插值定义在网格顶点上的 SDF 值来表示符号距离域

Volume Subdivision

为了提高效率，我们用从粗到细的方式来表示形状。我们通过检查四面体是否具有不同 SDF 符号的顶点来确定表面四面体 $T_{surf}$ -表明它与 SDF 编码的表面相交。我们将 $T_{surf}$ 及其近邻进行细分，并通过向每个边缘添加中点来提高分辨率。我们通过平均边缘上的 SDF 值来计算新顶点的 SDF 值(图 2)。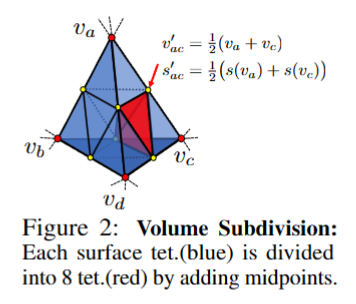
image.png|333

Marching Tetrahedra for converting between an Implicit and Explicit Representation

我们使用 Marching Tetrahedra[15]算法将编码的 SDF 转换为显式三角形网格。
给定四面体顶点的 SDF 值 $\{s(v_a),s(v_b),s(v_c),s(v_d)\}$， MT 根据 s(v)的符号确定四面体内部的表面类型，如图3所示。构型的总数为 $2^4 = 16$，在考虑旋转对称性后可分为 3 种独特的情况。一旦确定了四面体内部的曲面类型，在沿四面体边缘的线性插值的零交点处计算等距曲面的顶点位置，如图 3 所示。

Surface Subdivision

有一个表面网格作为输出允许我们进一步增加表示能力和形状的视觉质量与一个可微分的表面细分模块。我们遵循循环细分方法[35]的方案，但不是使用一组固定的参数进行细分，而是使这些参数在 DMTET 中可学习。具体来说，可学习的参数包括每个网格顶点 $v_{i}^{\prime}$ 的位置，以及 $\alpha_{i}$， $\alpha_{i}$ 通过加权相邻顶点的平滑度来控制生成的表面。注意，与 Liu et al.[33]不同，我们只在开始时预测每个顶点参数，并将其带入后续的细分迭代，以获得更低的计算成本。

DMTET: 3D Deep Conditional Generative Model

目的：从输入 x(点云或粗体素化形状)输出高分辨率 3D 网格 M

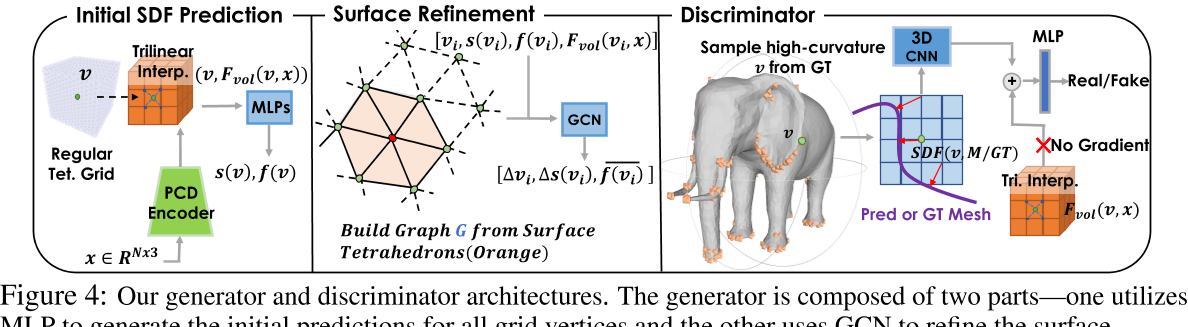
image.png|666

3D Generator

Input Encoder
点云：使用PVCNN[34]作为输入编码器，从点云中提取3D 特征体 $F_{vol}(x)$。
粗体素：我们在其表面采样点。我们通过三线性插值计算网格顶点 $v\in\mathbb{R}^3$ 的特征向量 $F_{vol}(v,x)$。

Initial Prediction of SDF
通过 MLP 预测每个顶点的 SDF：$s(v)=\boldsymbol{MLP}(F_{\boldsymbol{vol}}(v,x),v).$ 全连接网络还输出一个特征向量 f (v)，用于体细分阶段的表面细化

Surface Refinement with Volume Subdivision

Surface Refinement
在获得初始 SDF 后，迭代细化曲面并细分四面体网格。我们首先根据当前 s(v)值识别表面四面体 $T_{surf}$。然后我们建立一个图 $G=(V_{surf},E_{surf}),$，其中 $V_{surf},E_{surf}$ 对应于 $T_{surf}$ 中的顶点和边。然后，我们使用图形卷积网络 GCN[32]预测 $V_{surf}$ 中每个顶点 i 的位置偏移量 $\Delta v_{i}$ 和 SDF 残差值 $\Delta s(v_i)$

$\begin{array}{rcl}f_{v_i}^{\prime}&=&\operatorname{concat}(v_i,s(v_i),F_{vol}(v_i,x),f(v_i)),\end{array}$
$(\Delta v_i,\Delta s(v_i),\overline{f(v_i)})_{i=1,\cdots N_{surf}}\quad=\quad\mathrm{GCN}\big((f_{v_i}^{\prime})_{i=1,\cdots N_{surf}},G\big),$

通过 GCN，更新:

  • $v’_i=v_i+\Delta v_i$
  • $s(v’_i)=s(v_i)+\Delta s(v_i).$
  • $f_{v_i}^{\prime} \to \overline{f(v_i)}$

Volume Subdivision
在表面细化之后，我们执行体积细分步骤，然后执行附加的表面细化步骤。特别是，我们重新识别了 $T_{surf}$，并细分了 $T_{surf}$ 及其近邻。在这两个步骤中，我们都从完整的四面体网格中删除了未细分的四面体，这节省了内存和计算，因为 $T_{surf}$ 的大小与对象的表面积成正比，并且随着网格分辨率的增加呈二次而不是三次缩放。

注意，SDF 值和顶点的位置是从细分前的水平继承的，因此，在最终表面计算的损失可以反向传播到所有水平的所有顶点。因此，我们的 DMTET 自动学习细分四面体，并且不需要在中间步骤中添加额外的损失项来监督八叉树层次结构的学习，就像之前的工作 Octree Generating Networks 一样

Learnable Surface Subdivision
在 MT 提取表面网格后，我们可以进一步进行可学习的表面细分。具体来说，我们在提取的网格上构建一个新的图，并使用 GCN 来预测每个顶点的更新位置 $v_{i}^{\prime}$， $\alpha_{i}$ 用于循环细分。该步骤消除了量化误差，并通过调整 $\alpha_{i}$ 减轻了经典环路细分方法中固定的近似误差。

3D Discriminator

我们在生成器预测的最终表面上应用三维鉴别器 D。我们的经验发现，使用 DECOR-GAN[6]的3D CNN 作为从预测网格计算的带符号距离域的判别器可以有效地捕获局部细节。具体来说，我们首先从目标网格中随机选择一个高曲率顶点 v，在 v 周围的体素化区域计算地面真符号距离场 $S_{real}\in\mathbb{R}^{N\times N\times N}$。同样，我们在同一位置计算预测表面网格 M 的符号距离场，得到 $S_{pred}\in\mathbb{R}^{N\times N\times N}$。请注意，$S_{pred}$ 是网格 M 的解析函数，因此 $S_{pred}$ 的梯度可以反向传播到 M 中的顶点位置。我们将 $S_{real}$ 或 $S_{pred}$ 输入鉴别器，以及位置 v 中的特征向量 $F_{vol}(\bar{v},x)$，鉴别器然后预测指示输入是来自真实形状还是生成形状的概率。

Loss Function

  • a surface alignment loss to encourage the alignment with ground truth surface,
    • $L_{\mathrm{cd}}=\sum\limits_{p\in P_{pred}}\min\limits_{q\in P_{gt}}||p-q||_2+\sum\limits_{q\in P_{gt}}\min\limits_{p\in P_{pred}}||q-p||_2,L_{\mathrm{normal}}=\sum\limits_{p\in P_{pred}}(1-|\vec{\mathbf{n}}_p\cdot\vec{\mathbf{n}}_{\hat{q}}|),$
    • 从 GT 和 Pred 中分别采样一系列点 $P_{gt}$ 和 $P_{pred}$，计算两者之间的 L2 Chamfer Distance 和 normal consistency loss
  • an adversarial loss to improve realism of the generated shape, LSGAN 中提出
    • $L_{\mathbf{D}}=\frac{1}{2}[(D(M_{gt})-1)^{2}+D(M_{pred})^{2}],L_{\mathbf{G}}=\frac{1}{2}[(D(M_{pred})-1)^{2}].$
  • regularizations to regularize the behavior of SDF and vertex deformations.
    • 上述损失函数作用于提取的曲面上，因此，在四面体网格中，只有靠近等面的顶点接收梯度，而其他顶点不接收梯度。此外，表面损失不能提供内部/外部的信息，因为翻转四面体中所有顶点的 SDF 符号将导致 MT 提取相同的表面。这可能导致训练过程中分离的组件。为了缓解这个问题，我们增加了一个 SDF 损失来正则化 SDF 值
    • $L_{\mathrm{SDF}}=\sum_{v_i\in V_T}|s(v_i)-SDF(v_i,M_{gt})|^2,$
    • $SDF(v_i,M_{gt})$ 表示点 $v_i$ 到 GT mesh 的 SDF 值
    • 此外，预测顶点变形的正则化损失，避免伪影 $L_{\mathsf{def}}=\sum_{v_i\in V_T}||\Delta v_i||_2.$

最终的总损失：$L=\lambda_\mathrm{cd}L_\mathrm{cd}+\lambda_\mathrm{normal}L_\mathrm{normal}+\lambda_\mathrm{G}L_\mathrm{G}+\lambda_\mathrm{SDF}L_\mathrm{SDF}+\lambda_\mathrm{def}L_\mathrm{def},$

Conclusion

在本文中，我们介绍了一种深度 3D 条件生成模型，该模型可以使用简单的用户 guides（例如粗体素）来合成高分辨率 3D 形状。我们的 DMTET 具有一种新颖的 3D 表示，通过利用两者的优势来汇集隐式和显式表示。我们通过实验表明，我们的方法合成的质量形状明显更高，几何细节比现有方法更好，由定量指标和广泛的用户研究证实。通过展示提升粗体素（如 Minecraft 形状）的能力，我们希望我们一步更接近民主化 3D 内容创建。

Welcome to my other publishing channels