| Title | Rodin: A Generative Model for Sculpting 3D Digital Avatars Using Diffusion |
|---|---|
| Author | Tengfei Wang1† Bo Zhang2 Ting Zhang2 Shuyang Gu2 Jianmin Bao2 |
| Conf/Jour | arXiv preprint |
| Year | 2022 |
| Project | RODIN Diffusion (microsoft.com) |
| Paper | Rodin: A Generative Model for Sculpting 3D Digital Avatars Using Diffusion (readpaper.com) |
Abstract
本文提出了一种利用扩散模型自动生成以神经辐射场表示的三维数字化身的三维生成模型。生成这种虚拟形象的一个重大挑战是,3D 中的内存和处理成本令人望而却步,无法生成高质量虚拟形象所需的丰富细节。为了解决这个问题,我们提出了推出扩散网络(Rodin),它将神经辐射场表示为多个 2D 特征图,并将这些地图推出到单个 2D 特征平面中,我们在其中执行 3d 感知扩散。Rodin 模型在保证三维扩散完整性的同时,利用三维感知卷积,在二维特征平面中根据原始关系处理投影特征,从而提高了计算效率。我们还使用潜在条件反射来协调全局一致性的特征生成,从而产生高保真的虚拟形象,并使其基于文本提示进行语义编辑。最后,我们使用层次合成来进一步增强细节。与现有的生成技术相比,我们的模型生成的 3D 头像效果更好。我们可以生成具有逼真发型和胡须等面部毛发的高度详细的化身。我们还演示了从图像或文本生成 3D 头像以及文本引导的可编辑性。
Method

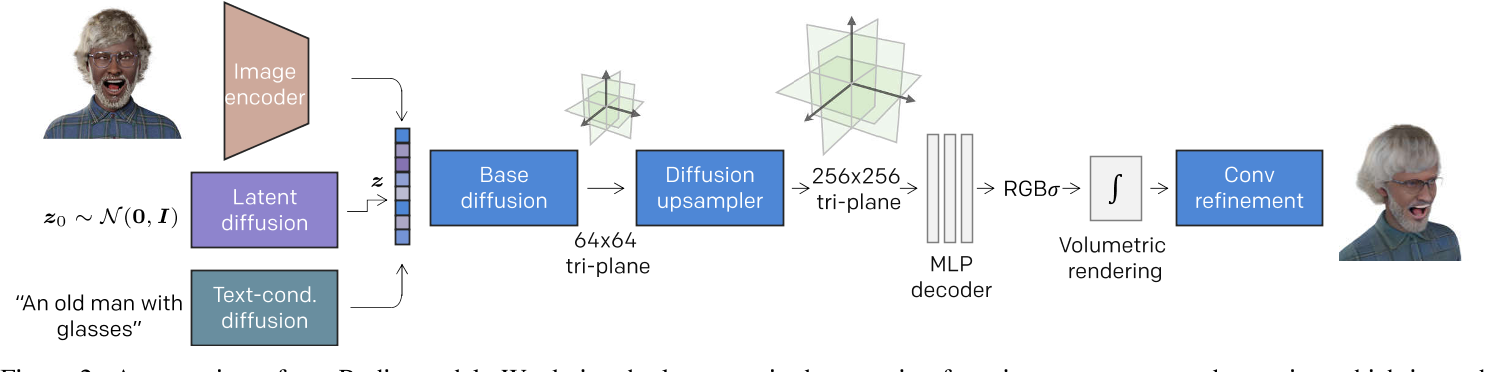
与之前从 2D 图像集合中学习 3D 感知生成的方法不同,我们的目标是使用来自 Blender 合成管道的多视图渲染来学习 3D 角色生成[69]。而不是将同一主题的多视图图像作为单独的训练样本,我们拟合每个头像的体积神经表示,用于解释从不同角度观察到的所有结果。然后,我们使用扩散模型来表征这些 3D 实例的分布。我们基于扩散的 3D 生成是一个分层过程-我们首先利用扩散模型生成粗糙的几何形状,然后是扩散上采样器进行细节合成。如图 2 所示,整个 3D 肖像生成包括多个训练阶段,我们将在下面的小节中详细介绍。
Robust 3D Representation Fitting
鲁棒的 3D 表示:
- 适合生成网络处理的显式表示
- 紧凑的表示,这是高效的的内存利用
- 表示可以快速拟合,原始 NeRF 那样耗时数小时的优化将无法生成生成建模所需的大量 3D 训练数据。
三维体被分解成三个轴向的正交特征平面 $y_{uv},y_{wu},y_{vw}\in\mathbb{R}^{H\times W \times C}$
每个特征平面的空间分辨率为 H×W,通道数为 c。与体素网格相比,三平面表示在不牺牲表达性的情况下提供了相当小的内存占用。因此,丰富的三维信息被显式地记忆在三平面特征中,可以通过将三维点 $p\in\mathbb{R}^3$ 投影到各个平面上,并将检索到的特征聚合在一起来查询其特征,即 $y_{p}=y_{uv}(p_{uv})+y_{wu}(p_{wu})+y_{vw}(p_{vw}).$
轻量级 MLP 解码器 $\mathcal{G}_\theta^{\mathrm{MLP}}$ 推导出给定观察方向 $d\in S^{2}$ 的每个 3D 位置的密度 $\sigma\in{\mathbb{R}^{+}}$ 和与视图相关的颜色 $c\in \mathbb{R}^{3}$,即:$c(p,d),\sigma(p)=\mathcal{G}_\theta^{\mathrm{MLP}}\big(y_p,\xi(y_p),d\big).$ 我们将傅里叶嵌入算子ξ(·)应用于查询的特征上,而不是空间坐标上。
对三平面特征和 MLP 解码器进行了优化,使得神经辐射场的渲染与给定主题的多视图图像 $\left\{x\right\}_{N_v}$ 匹配,其中 $x\in\mathbb{R}^{H_0\times W_0\times3}$。我们强制体积渲染[38]给出的渲染图像,即: $\hat{x}={\cal R}\left(c,\sigma\right),$,以均方误差损失匹配相应的地面真值。此外,我们还引入了稀疏、平滑和紧凑的正则化器来减少自由空间中的“浮动”伪像(Mip-NeRF 360)
虽然之前的每个场景重建主要关注拟合质量,但我们的 3D 拟合程序也应该考虑生成目的的几个关键方面。
- 首先,不同主体的三平面特征必须严格处于同一域。为了实现这一点,我们在拟合不同的肖像时采用了一个共享的 MLP 解码器,从而隐式地将三平面特征推到解码器可识别的共享潜在空间。
- 其次,MLP 解码器必须具有一定程度的鲁棒性。也就是说,解码器应该能够容忍三面特征的轻微扰动,因此即使三面特征不完全生成,仍然可以获得可信的结果。
- 更重要的是,解码器应该对不同的三平面尺寸具有鲁棒性,因为分层 3D 生成是在多分辨率三平面特征上训练的。如图 3 所示,当单独拟合 256 × 256 三平面时,其 64 × 64 分辨率变体无法有效呈现。为了解决这个问题,我们在拟合过程中随机缩放三平面,这有助于通过共享解码器同时导出多分辨率三平面特征。

Latent Conditioned 3D Diffusion Model
现在3D 角色生成被简化为学习三平面特征的分布,即 $p\left(y\right)$,其中 $y = (y_{uv},y_{wu},y_{vw})$。这种生成式建模是 non-trivial 的,因为 y 是高维的。我们利用扩散模型来完成这项任务,它在复杂的图像建模中显示出令人信服的质量
在较高的层次上,扩散模型通过逐步反转马尔科夫正演过程产生 y。从 $y_0\sim p(y)$ 开始,正演过程 q 根据 $y_t:=\alpha_t y_0+\sigma_t\epsilon,$ 得到一个递增的噪声潜码序列 $\{y_t\mid t\in[0,T]\}$,其中 $\epsilon\in\mathcal{N}(\mathbf{0},I)$ 为加入的高斯噪声;αt 和σt 定义了一个噪声调度,其对数信噪比 $\lambda_t=\log[\alpha_t^2/\sigma_t^2]$ 随时间步长 t 线性减小。有了足够的噪声步长,我们得到一个纯高斯噪声,即 $y_T \sim \mathcal{N}(0,I)$。生成过程对应于上述噪声过程的反转,其中扩散模型被训练成使用均方误差损失将 $y_{T}$ 降噪为 $y_{0}$。Following Denoising Diffusion Probabilistic Models.,通过参数化扩散模型 $\hat{\epsilon}_{\theta}$ 来预测增加的噪声,可以获得更好的生成质量: $\mathcal{L}_{\mathrm{simple}}=\mathbb{E}_{t,\boldsymbol{x}_0,\boldsymbol{\epsilon}}\bigg[\big|\hat{\epsilon}_{\boldsymbol{\theta}}(\alpha_t y_0+\sigma_t\boldsymbol{\epsilon},t)-\boldsymbol{\epsilon}\big|_2^2\bigg].$
在实践中,我们的扩散模型训练也共同优化了 41 中提出的变分下界损失 ${\mathcal{L}}_{\mathrm{VLB}}:$,从而可以用更少的时间步长实现高质量的生成。在推理过程中,使用随机祖先采样器 24 生成最终样本,该样本从高斯噪声 $y_T \sim \mathcal{N}(0,I)$ 开始,依次产生较少噪声的样本 $\{y_T,y_{T-1},\dots\}$,直到达到 y0。
我们首先训练一个基本扩散模型来生成粗糙的三平面,例如,在 64 × 64 分辨率下。
一种直接的方法是在我们的三平面生成中采用最先进的基于图像的扩散模型中使用的 2D 网络结构。具体而言,我们可以将通道维度中的三平面特征如[9]中所示进行串联,形成 $y=\left(\boldsymbol{y}_{uv}\oplus\boldsymbol{y}_{wu}\oplus\boldsymbol{y}_{vw}\right)\in\mathbb{R}^{H\times W\times3C},$ 并采用精心设计的二维 U-Net,通过去噪扩散过程对数据分布进行建模。然而,这样的基线模型会产生带有严重伪影的 3D 化身。我们推测生成伪影来自于三平面表示与二维 U-Net 之间的不兼容。
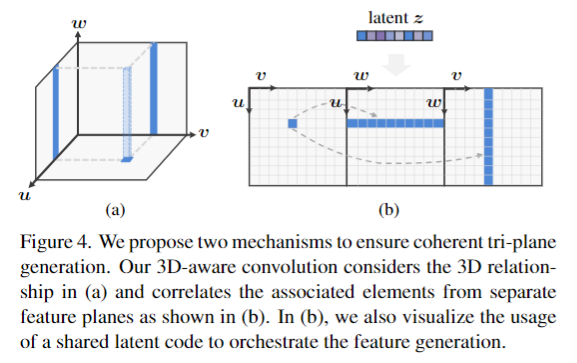
如图 4(a)所示,可以直观地将三平面特征视为神经体积在正面、底部和侧面的投影。因此,在 CNN 处理中,这些正交平面的通道级联是有问题的,因为这些平面在空间上没有对齐。为了更好地处理三平面表示,我们做了以下努力:
3D-aware convolution
使用 CNN 处理按通道拼接的三平面会导致在3D 方面混合理论上未校正的特征。解决这个问题的一个简单而有效的方法是在空间上展开三平面特征。如图4(b)所示,我们将三平面特征水平连接,得到 $\tilde{y}= \text{hstack}(y_{uv},y_{wu},y_{vw})\in\mathbb{R}^{H\times3W\times C}.$。这样的特征展开允许对特征平面进行独立处理。为简单起见,我们随后默认使用 y 来表示这样的输入形式。然而,三平面推出阻碍了跨平面通信,而 3D 生成需要三平面生成的协同作用。
为了更好地处理三平面特征,我们需要一个在三平面上执行的有效的 3D 算子,而不是将其视为普通的 2D 输入。为了实现这一点,我们提出了3D 感知卷积来有效地处理三平面特征,同时尊重它们的 3D 关系。在某一特征平面上的一个点实际上对应着体中的一条轴向三维直线,在其他平面上也有两条对应的直线投影,如图 4(A)所示。这些相应位置的特征本质上描述了相同的 3D 原语,应该同步学习。然而,当使用平面二维卷积进行三平面处理时,这种三维关系被忽略了。因此,我们的3D 感知卷积通过将每个平面的特征与其他平面的相应行/列相关联,明确地引入了这种 3D 感应偏置。通过这种方式,我们实现了 2D cnn 的 3D 处理能力。这种 3D 感知卷积应用于三平面表示,实际上是一种简化 3D 卷积的通用方法,以前在建模高分辨率 3D 体积时计算成本太高。
3d 感知卷积如图4(b)所示。理想情况下,$y_{uv}$ 的计算将关注来自其他平面的相应行/列的完整元素,即 $y_{wu}$ 和 $y_{vw}$。对于并行计算,我们将其简化并聚合行/列元素。具体来说,我们对 $y_{wu}$ 和 $y_{vw}$ 应用了轴向池化,分别得到一个行向量 $y_{wu\to u}\in\mathbb{R}^{1\times W\times C}$ 和一个列向量 $y_{vw\to v}\in\mathbb{R}^{H\times 1\times C}$。对于 $y_{uv}$ 的每个点,我们可以很容易地访问聚合向量中相应的元素。我们将聚合向量扩展到原来的二维维度(即沿行维度复制列向量,反之亦然),从而得到 $y_{(\cdot)u},y_{v(\cdot)}\in\mathbb{R}^{H\times W\times C}$。到目前为止,我们可以对特征映射的通道级连接执行2D 卷积,即 $\text{Conv2D}(\boldsymbol{y}_{uv}\oplus\boldsymbol{y}_{(\cdot)u}\oplus\boldsymbol{y}_{v(\cdot)}).$。因为 $y_{uv}$ 现在在空间上与来自其他平面的相应元素的聚合对齐。对 $y_{wu}$ 和 $y_{vw}$ 进行了同样的计算。3d 感知卷积极大地增强了平面间的通信,我们通过经验观察到减少了伪影,并改善了头发等细结构的生成。
Latent conditioning.
我们进一步提出学习一个潜在向量来协调三平面生成。如图2所示,我们另外训练了一个图像编码器 $\mathcal{E}$ 来提取一个语义潜在向量作为基本扩散模型的条件输入,所以本质上整个框架就是一个自编码器。具体来说,我们从每个训练对象的正面视图中提取潜在向量,即 $z=\mathcal{E}_\theta(x_{\mathrm{front}})\in\mathbb{R}^{512},$ 训练以 z 为条件的扩散模型重构同一主体的三平面。我们使用自适应群归一化(AdaGN)来调节扩散模型的激活,其中 z 注入到每个残差块中,这样,根据共享潜函数同步生成正交平面的特征。
潜在条件反射不仅可以提高生成质量,还可以提供一个解纠缠的潜在空间,从而可以对生成的结果进行语义编辑。为了实现更好的可编辑性,我们采用了与文本提示共享潜在空间的冻结 CLIP 图像编码器[48]。我们将展示学习模型如何产生可控的文本引导生成结果。
潜在条件反射的另一个显著优点是它允许无分类器的引导,这是一种通常用于提高条件生成中的采样质量的技术。在训练扩散模型时,我们以20%的概率随机将潜在嵌入归零,从而使扩散解码器适应无条件生成。在推理过程中,我们可以根据 $\hat{\epsilon}_\theta(y,z)=\lambda\epsilon_\theta(y,z)+(1-\lambda)\epsilon_\theta(y),$ 引导模型朝着更好的 generation sampling 方向发展
- 其中 $\epsilon_\theta(y,z) \text{and}\epsilon_\theta(y)$ 分别为条件预测和无条件预测,λ > 0 为引导强度。
因此,我们的潜在条件基础模型既支持无条件生成,也支持用于肖像反演的条件生成。为了考虑无条件采样期间的完全多样性,我们额外训练了一个扩散模型来模拟潜在 z 的分布,而潜在 $y_{T}$ 描述残差变化。我们在图 2 中包含了这个潜在扩散模型。
Diffusion Tri-plane Upsampler
为了生成高保真的3D 结构,我们进一步训练扩散超分辨率(SR)模型,将三平面分辨率从64×64提高到256×256。在这个阶段,扩散上采样器的条件是低分辨率(LR)三平面 $y^{\mathrm{LR}}$。与基本模型训练不同的是,我们将扩散上采样器 $y_{\theta}^{\mathrm{HR}}(y_{t}^{\mathrm{HR}},y^{\mathrm{LR}},t)$ 参数化来预测高分辨率(HR)地面真值 $y_0^{\mathrm{HR}}$,而不是 added 噪声 $\epsilon.$。在每个残差块中利用三维感知卷积来增强细节合成。
在之前的级联图像生成工作之后,我们应用条件增强来减少基本模型输出和 LR 条件输入之间的域间隙,用于 SR 训练。我们通过随机下采样、高斯模糊和高斯噪声的组合对三平面增强进行了仔细的调整,使渲染增强的 LR 三平面尽可能地与基本渲染输出相似。
尽管如此,我们发现与地面真实较低 L2距离的三平面恢复不一定对应于令人满意的图像渲染。因此,我们需要直接约束渲染的图像。具体来说,我们从预测的三平面 $\hat y_{0}^{HR}$ 中获得了渲染图像 $x^{\hat{\mathrm{HR}}}\in\mathbb{R}^{256\times256\times3}$,其中 $\hat{\boldsymbol{x}}=\mathcal{R}(\mathcal{G}_{\theta}^{\mathbf{MLP}}(\hat{\boldsymbol{y}}_{0}^{\mathbf{HR}}))$,我们进一步惩罚了这个渲染结果与地面真实之间的感知损失[27],根据 $\mathcal{L}_{\mathtt{perc}}=\mathbb{E}_{t,\hat{\boldsymbol{x}}}\sum\lVert\Psi^l(\hat{\boldsymbol{x}})-\Psi^l(\boldsymbol{x})\rVert_2^2,$ 其中 $\Psi^l$ 表示使用预训练的 VGG 进行多级特征提取。
通常,体绘制需要沿每条射线分层采样,这对于高分辨率渲染来说在计算上是禁止的。因此,我们在人脸区域具有高采样重要性的随机112 × 112图像块上计算 $\mathcal{L}_{perc}$。与之前需要渲染完整图像的 3d 感知 gan 相比,我们的 3d 感知 SR 可以很容易地扩展到高分辨率,因为允许在直接监督下进行 patchwise 训练
$\mathcal{L}_{perc}$ 是 patchwise 的
建模高频细节和薄结构是特别具有挑战性的体绘制。因此,在这个阶段,我们在我们的数据上共同训练一个卷积细化器,它补充了NeRF渲染中缺失的细节,最终产生引人注目的1024 × 1024图像输出。
Conclusion
从实验中,我们观察到 Rodin 模型是一个强大的 3D 头像生成模型。这种模式还允许用户从肖像或文字中定制头像,从而大大降低了个性化头像创建的障碍。虽然本文只关注虚拟人物,但罗丹模型背后的主要思想适用于一般 3D 场景的扩散模型。事实上,高昂的计算成本一直是 3D 内容创作的一大挑战。在 3D 中执行连贯和 3D 感知扩散的高效 2D 架构是解决这一挑战的重要一步。在今后的工作中,提高三维扩散模型的采样速度,共同研究利用充足的二维数据来缓解三维数据瓶颈将是富有成效的。