QiYun

Note

Adaptive Shells

Posted on Edited on In
4.5k 17 mins.
Title Adaptive Shells for Efficient Neural Radiance Field Rendering
Author Zian Wang and Tianchang Shen and Merlin Nimier-David and Nicholas Sharp and Jun Gao and Alexander Keller and Sanja Fidler and Thomas M\”uller and Zan Gojcic
Conf/Jour ACM Trans. On Graph. (SIGGRAPH Asia 2023)
Year 2023
Project Adaptive Shells for Efficient Neural Radiance Field Rendering (nvidia.com)
Paper Adaptive Shells for Efficient Neural Radiance Field Rendering (readpaper.com)

image.png|666

Abstract

神经辐射场在新视图合成中实现了前所未有的质量，但它们的体积公式仍然昂贵，需要大量的样本来渲染高分辨率图像。体积编码对于表示模糊几何(如树叶和毛发)是必不可少的，它们非常适合于随机优化。然而，许多场景最终主要由固体表面组成，这些表面可以通过每个像素的单个样本精确地渲染。基于这一见解，我们提出了一种神经辐射公式，可以在基于体积和基于表面的渲染之间平滑过渡，大大加快渲染速度，甚至提高视觉保真度。
我们的方法构建了一个明确的网格包络，该包络在空间上约束了神经体积表示。在固体区域，包络几乎收敛到一个表面，通常可以用单个样本渲染。为此，我们推广了 NeuS [Wang et al. 2021]公式，使用学习的空间变化核大小来编码密度的传播，将宽核拟合到类体积区域，将紧核拟合到类表面区域。然后，我们在表面周围提取一个窄带的显式网格，宽度由核尺寸决定，并微调该波段内的辐射场。在推断时，我们将光线投射到网格上，并仅在封闭区域内评估辐射场，大大减少了所需的样本数量。实验表明，我们的方法可以在非常高的保真度下实现高效的渲染。我们还演示了提取的包络支持下游应用程序，如动画和仿真。

Introduction

使用 InstantNGP 加速：nerf 已经可以渲染每条射线具有不同数量的样本的图像

  • 首先，基于网格的加速结构的内存占用随着分辨率的增加而减少
  • 其次，mlp 的平滑感应偏置阻碍了学习体积密度的尖锐脉冲或阶跃函数，即使学习了这样的脉冲，也很难有效地对其进行采样
  • 最后，由于缺乏约束，隐式体积密度场不能准确地表示下表面 underlying surfaces—— NeuS [Wang et al. 2021]，这往往限制了它们在依赖网格提取的下游任务中的应用

为了弥补最后一点，[Wang et al. 2021, 2022a;Yariv 等人]提出优化带符号距离函数(SDF)以及编码密度分布的核大小，而不是直接优化密度。虽然这对于改善表面表示是有效的，但使用全局核大小与场景的不同区域需要自适应处理的观察相矛盾。

为了解决上述挑战，我们提出了一种新的体积神经辐射场表示方法。特别是:
I)我们概括了 NeuS[Wang et al .2021]的公式，该公式具有空间变化的核宽度，对于模糊表面收敛为宽核，而对于没有额外监督的固体不透明表面则坍缩为脉冲函数。在我们的实验中，仅这一改进就可以提高所有场景的渲染质量。
Ii)我们使用学习到的空间变化核宽度来提取表面周围窄带的网格包络。提取的包络的宽度可以适应场景的复杂性，并作为一种有效的辅助加速数据结构。
Iii)在推断时，我们将光线投射到包络层上，以便跳过空白区域，并仅在对渲染有重要贡献的区域对辐射场进行采样。在类表面区域，窄带可以从单个样本进行渲染，而对于模糊表面则可以进行更宽的核和局部体渲染。

Neural Radiance Fields (NeRFs).

Implicit surface representation.
我们的方法是建立在 NeuS 公式之上，我们的主要目标不是提高提取表面的准确性。相反，我们利用 SDF 提取一个狭窄的外壳，使我们能够适应场景的局部复杂性，从而加速渲染

Accelerating neural volume rendering.
我们研究了一种加速(体积)渲染的替代方法，通过调整渲染每个像素所需的样本数量来适应场景的潜在局部复杂性。请注意，我们的公式是对“烘焙”方法的补充，我们认为两者的结合是未来研究的有趣途径。

Method

我们的方法(见图 3)建立在 NeRF 和 NeuS 的基础上。具体来说，我们概括了 NeuS 使用新的空间变化核(章节 3.2)，提高了质量并指导窄带壳的提取(章节 3.3)。然后，在 shell 内对神经表示进行微调(第 3.5 节)，从而显著加速渲染(第 3.4 节)。

Preliminaries

直观上，一个小的𝑠会得到一个具有模糊密度的宽核，而在限界 $\lim_{\mathfrak{s}\to0}d\Phi_\mathbf{s}/d\tau$ 中，则近似于一个尖锐的脉冲函数(见插图)。这种基于 sdf 的公式允许在训练期间使用 Eikonal 正则化器，这鼓励学习的𝑓成为实际的距离函数，从而产生更准确的表面重建。相关的损失将在第 3.5 节中讨论。

(NeuS 对 $\Phi_s(f)=(1+\exp(-f/s))^{-1},$ 中 s 的修改即核大小，修改密度变化 $\sigma=\max\left(-\frac{\frac{d\Phi_s}{d\tau}(f)}{\Phi_s(f)},0\right)$) 趋势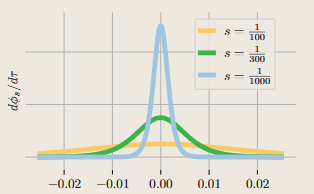
image.png|333

==后面的 s 都是核大小==

Spatially-Varying Kernel Size

NeuS SDF 公式是非常有效的，然而，它依赖于全局核大小。结合 Eikonal 正则化，这意味着在整个场景中体积密度的恒定分布。然而，一刀切的方法并不能很好地适应包含“尖锐”表面(如家具或汽车)和“模糊”体积区域(如头发或草)混合的场景。

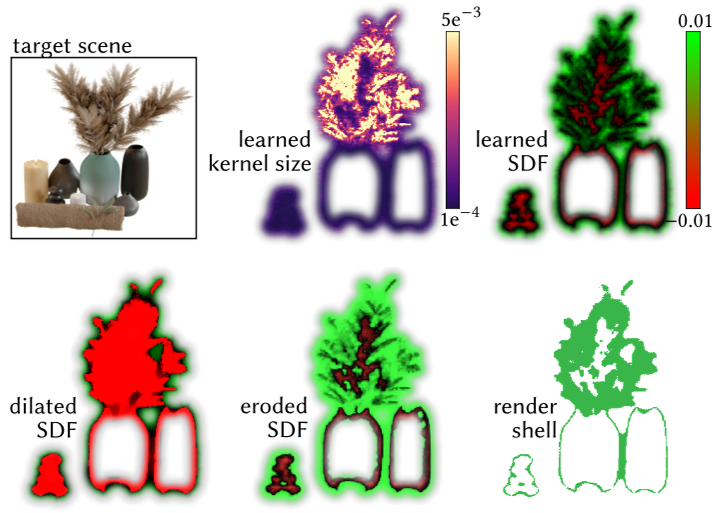
我们的第一个贡献是用一个空间变化的、局部学习的核大小𝑠作为依赖于输入 3D 位置 x 的额外神经输出来增强 NeuS 公式。扩展的网络变成 $(\mathbf{c},f,s)=\mathrm{NN}_{\theta}(\mathbf{x},\mathbf{d})$ (参见第 4.1 节中的实现细节)。在训练过程中，我们还加入了一个正则化器来提高核大小 field 的平滑度(第 3.5 节)。该神经场仍然可以仅从彩色图像监督中进行拟合，并且由此产生的随空间变化的核大小会自动适应场景内容的清晰度(图 7)。这种增强的表示本身是有价值的，可以提高困难场景中的重建质量，但重要的是它将指导我们在 3.3 节中明确的 Shell 提取，从而大大加快渲染速度。

Extracting an Explicit Shell

自适应壳划分了对渲染外观有重要影响的空间区域，并由两个显式三角形网格表示。当𝑠较大时，外壳较厚，对应于体积场景内容，当𝑠较小时，外壳较薄，对应于表面。在隐式 field 𝑠和𝑓按照 3.2 节的描述进行拟合之后，我们作为后处理提取这个自适应 shell 一次。

在方程3中 $\Phi_s(f)=(1+\exp(-f/s))^{-1},$ $\sigma=\max\left(-\frac{\frac{d\Phi_s}{d\tau}(f)}{\Phi_s(f)},0\right)$
S 形指数中数量𝑓/𝑠的大小决定了沿着一条射线的渲染贡献(参见第 3.1 节的插图)。简单地提取|𝑓/𝑠| <𝜂(对于某些𝜂)作为对呈现有重要贡献的区域是很有诱惑力的。然而，学习到的函数很快就会在远离𝑓= 0 水平集的地方变得有噪声，并且在不破坏精细细节的情况下无法充分正则化。我们的解决方案是分别提取内部边界作为𝑓= 0 水平集的侵蚀，并将外部边界作为其膨胀(图 4)，两者都通过针对任务定制的正则化约束水平集进化来实现

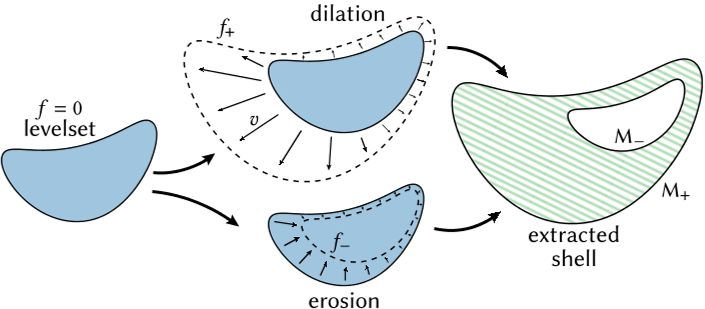
image.png|666

详细地说，我们首先对规则网格顶点处的 field 𝑓和𝑠进行采样。然后，我们将水平集进化应用于𝑓，产生新的侵蚀场 SDF-，并通过 marching cubes 提取 SDF- = 0 水平集作为内壳边界。一个独立的、类似的演化产生了膨胀场 SDF+，而 SDF+ = 0 的能级集形成了外壳边界。
我们分别定义这两个 level 集:

  • 膨胀的外表面应该是光滑的，以避免可见的边界伪影，
  • 而侵蚀的内表面不需要光滑，但必须只排除那些肯定对渲染外观没有贡献的区域。

Recall field 𝑎的基本水平集演化由 $\partial a/\partial t=-\left|\nabla a\right|v$ 给定，其中𝑣是水平集的所需标量向外法向速度。我们在𝑓上的限制的正则化流是：$\frac{\partial f}{\partial t}=-|\nabla f|\left(v(f_{0},s)+\lambda_{\mathrm{curv}}\nabla\cdot\frac{\nabla f}{|\nabla f|}\right)\omega(f),$
其中 $𝑓_{0}$ 表示初始学习的 SDF，散度项是一个权值为 $𝜆_{curv}$ 的曲率平滑正则化器。软衰减𝜔(见插图)将流量限制在水平集周围的窗口:
窗口宽度𝜁。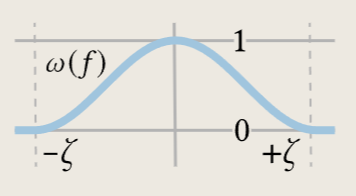
image.png|333

为了 dilate 水平集，对于法线方向入射的射线，选择速率 v用密度为 $\sigma>\sigma_{\min}$ 填充所有区域

$v_\text{dilate}(f_0,s)=\begin{cases}\beta_d\sigma(f_0,s)&\sigma(f_0,s)>\sigma_{\min}\\0&\sigma(f_0,s)\leq\sigma_{\min}\end{cases},$

$\beta_{d}$ 是 scaling coefficient。我们使用𝜁= 0.1，$𝜆_{curv} = 0.01$。

为了侵蚀水平集，速度与密度成反比，因此在低密度区域，壳向内膨胀得快，而在高密度区域，壳向内膨胀得慢

$v_{\mathrm{erode}}(f_0,s)=\min{(v_{\mathrm{max}},\beta_e}\frac{1}{\sigma(f_0,s)}),$

这里我们使用𝜁= 0.05，$𝜆_{curv}$ = 0。These velocities 导致了短距离的流动，因此形成了一个狭窄的壳，其中𝑠很小，内容物呈表面状。它们导致长距离流动，因此形成一个宽壳，其中𝑠很大，内容物呈体积状。

我们通过前向欧拉积分法在网格上对该流进行50步积分，通过空间有限差分计算导数，分别计算膨胀场 SDF+和侵蚀场 SDF-。我们认为没有必要进行数值上的距离调整。最后，我们将结果 $SDF−←max(𝑓_{0},SDF−)$ 和 $SDF+←min(𝑓_0,SDF+)$ 夹紧，以确保侵蚀场只缩小水平集，而膨胀流只增大水平集。SDF+ = 0 和 SDF−= 0 的水平集通过 MC 分别作为外壳外边界网格 M+和内壳边界网格 M−提取。图 5 显示了结果字段。进一步详情载于附录的程序1及2。

image.png|666

Narrow-Band Rendering

提取的自适应壳作为辅助加速数据结构，引导点沿着射线采样(公式 2)，使我们能够有效地跳过空白空间，只在需要高感知质量的地方采样点。对于每条射线，我们使用硬件加速射线跟踪来有效地枚举由射线和自适应壳的交点定义的有序间隔。在每个间隔内，我们查询等间隔的样本。我们的渲染器不需要任何动态自适应采样或依赖于样本的终止标准，这有利于高性能并行评估。

详细地说，我们首先为外部网格 M+和内部网格 M-
构建光线跟踪加速数据结构，然后将每条光线投射到网格上，产生一系列光线进入或退出网格的交叉点，将光线划分为零或更多包含在外壳中的间隔(见插图)。

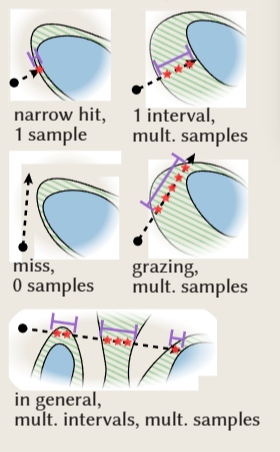
image.png|222

采样数量计算方法：$ceil(max(w-w_s,0)/{\delta_{s}})+1$，将最大采样数量限制为 $N_{max}$，并等距离采样
这个过程可以通过首先生成所有间隔内的所有样本，然后执行单个批处理 MLP 推理传递来实现，这可以提高吞吐量

Losses and Training

在第一阶段
$\mathcal{L}=\mathcal{L}_{\mathbf{c}}+\lambda_{e}\mathcal{L}_{e}+\lambda_{s}\mathcal{L}_{s}+\lambda_{\mathbf{n}}\mathcal{L}_{\mathbf{n}}$

  • 所有实验的权值分别为𝜆c = 1， 𝜆𝑒= 0.1，𝜆n = 0.1，𝜆𝑠= 0.01。
  • $\mathcal{L_{c}}$ 是对校准的真地图像的标准逐像素色彩损失：$\mathcal{L}_{\mathrm{c}}=\frac{1}{|\mathcal{R}|}\sum_{\mathrm{r}\in\mathcal{R}}|\mathbf{c}(\mathbf{r})-\mathbf{c}_{\mathrm{gt}}(\mathbf{r})|$
  • $\mathcal{L_{e}}$ 是 Eikonal 正则器 $\mathcal{L}_{e}=\frac{1}{|X|}\sum_{\mathbf{x}\in\mathcal{X}}\left(||\nabla f(\mathbf{x})||_{2}-1\right)^{2},$ 本文使用有限差分得到
  • 损失 $\mathcal{L_{s}}$ 正则化在我们的公式中引入的空间变化的核大小以实现平滑: $\mathcal{L}_{s}=\frac{1}{\mathcal{X}}\sum_{\mathbf{x}\in\mathcal{X}}|||\log\big[s(\mathbf{x})\big]-\log\big[s(\mathbf{x}+\mathcal{N}(0,\varepsilon^{2}))\big]||_{2},$ 式中 $\mathcal{N}(0,\varepsilon^{2})$ 为标准差为 $\varepsilon$ 的正态分布样本。最后，我们把损失算进去
  • $\mathcal{L}_{\mathbf{n}}=\frac{1}{|\mathcal{X}|}\big|\mathbf{n}(\mathbf{x})-\frac{\nabla f(\mathbf{x})}{||\nabla f(\mathbf{x})||_{2}}\big|_{2},$ 与 NeuS 一样，我们将利用几何法线作为着色子网络的输入，但我们发现使用网络预测这些法线可以提高推理性能，而不是梯度评估

在隐式域拟合之后，我们提取自适应壳，如第3.3节所示。虽然最初的训练需要沿着射线密集采样，但我们的显式外壳现在允许窄带渲染只在重要区域集中样本。因此，我们在窄带内微调表示，现在只有 $\mathcal{L_{c}}$ -不再需要鼓励几何上很好的表示，因为我们已经提取了外壳并将采样限制在场景内容周围的小带内。禁用正则化使网络能够将其全部容量用于拟合视觉外观，从而提高视觉保真度(表 4)。在附录的过程 4 中，我们还提供了带有算法细节的训练管道。

  • 第二阶段只需要优化 $\mathcal{L_{c}}$

APPLICATIONS

  • Cage-based deformation methods 动态物体（变形网格）
  • physical simulation and animation

DISCUSSION

最近的工作开发了加速和提高 nerf 类场景表示质量的方案。第 4 节提供了对选定的，特别是相关方法的比较。请注意，由于该领域的高研究活动，不可能对所有技术进行比较，并且许多方法的实现是不可用的。因此，我们对一些相关工作提出补充意见:

  • MobileNeRF、nerfmesh 和 nerf2mesh 后处理类似 nerf 的模型并提取网格以加速推理，类似于这项工作。然而，这些方法将外观限制在表面，牺牲了质量。相反，我们的方法保留了完整的体积表示和几乎完全的 nerf 质量，代价是稍微昂贵一些的推理(尽管在现代硬件上仍然是实时的)。
  • DuplexRF 也从底层神经领域提取了一个显式外壳，并使用它来加速渲染，尽管它使用了非常不同的神经表示，优先考虑性能。它们的壳直接从辐射场的两个阈值中提取，这需要仔细选择阈值，并导致与我们的方法相反的噪声壳不适应场景的局部复杂性。
  • VMesh 基于类似的见解，即场景的不同部分需要不同的处理。然而，它们的公式假设了一个额外的体素网格数据结构来标记有助于最终渲染的体积区域。与InstantNGP的辅助加速数据结构一样，这种方法的复杂性缩放能力较差。相反，我们的方法使用显式的自适应shell来划分有助于呈现的区域。除了较低的复杂性外，我们的配方无缝地支持第5节APPLICATIONS中讨论的进一步应用

CONCLUSION AND FUTURE WORK

在这项工作中，我们专注于有效地渲染nerf。我们的第一阶段训练(第3.2节)在很大程度上类似于NNeuralangelo，并且可能通过算法进步和类似于我们的推理管道的低级调优来加速NeuS。
尽管我们的方法为高保真神经渲染提供了很大的加速，并在现代硬件上以实时速率运行(表1)，但它仍然比MeRF等方法昂贵得多，其预先计算神经场输出，并将其烘烤成离散的网格表示。我们的公式与MeRF的公式是互补的，我们假设结合这两种方法将导致进一步的加速，潜在地达到性能-高质量的方法，将体积表示烘烤到显式网格，甚至可以在商品硬件上实时运行(例如MobileNeRF)。
我们的方法不能保证捕获薄结构——如果提取的自适应壳忽略了一个几何区域，它将永远无法在微调期间恢复，并且将始终缺席重建。这种形式的工件在一些mipnerf360场景中是可见的。未来的工作将探索一个迭代过程，在这个过程中，我们交替调整我们的重建和适应外壳，以确保没有重要的几何形状丢失。在我们的重建中偶尔出现的其他人工制品包括虚假的浮动几何形状和低分辨率背景;这两者都是神经重建中常见的挑战，我们的方法可以借鉴该领域其他工作的解决方案(例如RegNeRF)。
更广泛地说，将最近的神经表示与计算机图形学中实时性能的高性能技术结合起来有很大的潜力。在这里，我们展示了如何使用光线跟踪和自适应shell来极大地提高性能

Welcome to my other publishing channels