Basic of Finite Element Analysis
Finite Element
有限元分析（Finite Element Analysis，FEA）有时又被称作有限元方法（Finite Element Method，FEM），二者基本可以混用，微小的区别在于，FEM 侧重于整套理论而 FEA 侧重于应用 FEM 于具体工程问题。
Basic
有限元入门—Understanding the Finite Element Method | The Efficient Engineer的部分笔记 - 知乎
网格划分：六面体和四面体该怎么选择？ - 知乎 六面体计算收敛速度快，四面体计算收敛慢。
有限元分析（FEA）是个什么东东 - 知乎 有限元法就是为了求解偏微分方程！ 获得微分方程的“弱形式”解
有限元模型是什么：
- 节点nodes和元素/单元elements的集合称为有限元网格(finite element mesh)
- 元素elements：线元素line elements用于建模杆等一维结构、表面元素surface elements用于模拟薄壳等薄表面、实体元素solid elements用于建模三维实体，如四面体Tet，六面体Hex
- 复杂的几何体通常只能使用tri三角形和tet四面体元素进行网格划分。四边形quad和六面体hex元素最适合规则几何图形，在规则几何图形中，它们优于三角形和三角形元素，因为它们效率更高且需要的节点更少
- 元素可以是线性的（也称为一阶元素，linear or first-order elements）或二次的（二阶元素，quadratic or second-order elements）。二次元素在元素的每一侧都有附加的中间节点。它们需要更多的计算能力，但通常比线性元素产生更准确的结果。线性四面体元素（例如TET4，一种4节点四面体元素）可能表现出过度僵硬的行为，应避免使用它们-通常应使用TET10二次四面体元素
- 自由度：有限元网格中的每个节点都有一定数量的自由度，在二维应力分析中，每个节点有3个自由度——在X轴和Y轴上平移，以及绕Z轴旋转。对于热分析，每个节点都有一个自由度，即节点温度。
- 微分方程大大降低了使用固体力学法的效率，甚至让求解成为不可能
- 那么怎样才能绕开微分方程呢？答案是在计算一开始就去猜结构受力后的位移。这个位移最好满足边界条件（注意，这里是“最好”），之后算出结构在假设位移下的内外力虚功，或者是应变能，令其满足对应的能量原理。人们通过猜位移并引入能量原理的方式终于摆脱了微分方程，可以通过积分来分析结构了。
- 用传统书写方式进行计算效率贼低，一大堆类似的方程算来算去，好不自在。于是有人引入了矩阵（Matrix）来改善计算效率，把相似计算写成矩阵形式，使得书写更加简洁，效率也更高。
- 把结构分成很多很多份，去猜每一份上的位移，比如都猜成线性，只要结构被划分的够多，每一份上猜的准不准就无所谓，在满足收敛条件的前提下，算出来的位移就会很靠近真实的位移
试函数（_trial function_）作为有限元分析的数学基础，其基本原理是：先假定满足一定边界条件的试函数，然后将其代入需要求解的控制方程（_governing equation_），通过使用与原方程的误差残值最小来确定试函数中的待定系数。
求解微分方程方法：
- 解析方法
- 近似方法(差分)，将整体分为很多小部分，每个部分进行求解，细分越多越接近解析解
- 近似方法(试函数)，选择满足边界条件的试函数(有待定系数)，带入控制方程(微分方程)，大概率不满足方程，带入控制方程得到残差函数并让残差最小。加权余量法——(残差函数与基底函数加权求和/求积分并令其为0，确当待定系数) 当残差与基函数的积分为零时，意味着在这些方向上的残差投影为零。
Really nice book!!!
有限元方法（一）【翻译】 | 学习笔记
《Automated Solution of Differential Equations by the Finite Element Method》读书笔记 by chaoskey
PINN
PINN相较于FEM加了data driven，相较于Neural network加了物理先验信息
(72 封私信 / 80 条消息) 数值pde与深度学习结合是未来发展方向吗？ - 知乎 PINN 内嵌物理知识神经网络（PINN）是个坑吗？ - 知乎
数值pde与深度学习结合是未来发展方向吗？ - Martingale的回答 - 知乎
PINN还有研究的必要吗？ - 可恶的大黑狗的回答 - 知乎 https://www.zhihu.com/question/526459912/answer/3431672289
在我看来，传统的有限体积法有限元法本身就可看做训练好的图神经网络
广义来看，Physically Compatible 3D Object Modeling from a Single Image 这篇是不是也是PINN，基于物理来优化三维模型，让重建出来的三维模型打印后可以合理地立在桌面上
内嵌物理知识神经网络（PINN）是个坑吗？ - 知乎 PINN基本原理
数值分析类教材中接触得更多的是有限差分法、有限元、有限体积法等的基于网格的方法。还存在与基于网格方法相对的一类方法，也就是所谓无网格方法，在其中不难发现PINN的原型（Prototype），比如一种最简单的基于强形式径向基函数的无网格方法Kansa法。
PINN：
对于微分方程$\begin{aligned}\mathcal{F}(u(z);\gamma)&=f(z)\quad&&z\in\Omega\\\mathcal{B}(u(z))&=g(z)\quad&&z\in\partial\Omega\\\mathcal{D}(u(z_i))&=d(z_i)\quad&&i\in D\end{aligned}$
- $z$是包含了空间和时间的坐标；
- $u$表示方程的解；
- $\Omega$是方程所在的区域；
- $\mathcal{F}$算子描述了控制方程；
- $\gamma$是控制方程的参数；
- $\mathcal{B}$算子描述了初值或者边界条件，
- $\mathcal{D}$算子描述了观测数据的方式；
- $D$是观测数据指标集。
PINN目的就是求解$u$，用神经网络来逼近这个解$u_\theta(z)\approx u(z),\quad z\in\Omega.$，这里的时空信息都被包含在$z$中，也就可以关于$z$进行自动微分运算来表达 $\mathcal{F},\mathcal{B},\mathcal{D}$这些微分算子，这只是个最基本的模型，也就是Raissi 2017年底提出的一个网络模型，目前也被使用得最多。其他加入了Resnet、soft-attention、Echo State Network的结构也不鲜见，总之，这类结构可以对$z$求自动微分。
深度学习一些其他网络结构，比如CNN、RNN，通常并没有直接可供直接输入空间或时间 z 的入口，而是将空间或时间的信息直接嵌入到网络本身的结构中。CNN类方法的图像信号天然包含空间信息，RNN类方法的处理单元天然包含时间信息。然后依据“内嵌物理知识”这一思想，将微分方程的三个算子$\mathcal{F},\mathcal{B},\mathcal{D}$ 以离散（差分）的方式而不是自动微分的方式嵌入到损失函数中，有时这种内嵌物理的方式会被它们的作者称为是“弱监督”、“自监督”或者“无监督”。狭义的PINN并不包含这类不使用自动微分的结构，虽然“内嵌物理”的思想上并没有太大区别。
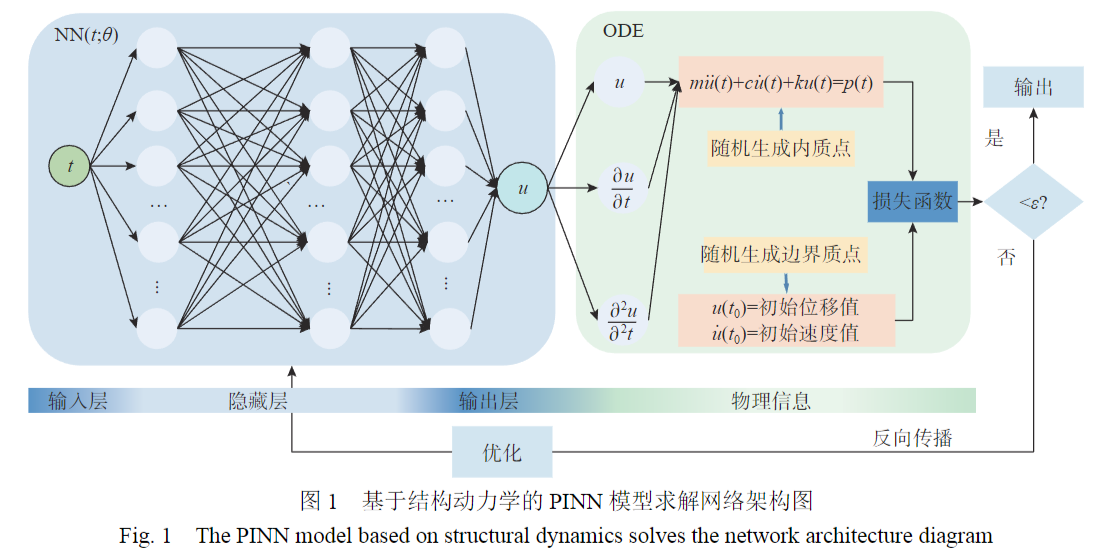
VEM (Virtual Element Method)
草莓Ye子酱个人动态-草莓Ye子酱动态记录-哔哩哔哩视频 Qinxiaoye/xpfem: A python package for finite element method (FEM) in solid mechanics Bingbing Xu大佬
An introduction to the Virtual Element Method
Software (about FE)
Solidworks
建立好的模型导出为.x_t格式
将Solid 转换成Surface：
- Delete Face
- Offset
How To Convert Solid To Surface Body In SolidWorks - YouTube
Patran
Preferences —> Geometry 单位制 inches/m/mm，不同的单位设置材料特性时会有差异
eg(钢板): E = 210GPa，$\rho = 7860 Kg/m^{3}$
mm制：
- Elastic Modulus/Shear Modulus：(210000)MPa/(83000)MPa
- Poisson Ratio(0.25)：注意设置了E和G后，Poisson Ratio会自动计算(根据钢板算例测试出来的)
- Density：(7.8599998E-09)$Kgf \cdot s^{2} /mm^{4}$ $(Kg/m^{3} =kgf \cdot s^{2}/m^{4})$ $(1Kgf = 9.8N = 9.8 Kg \cdot m/s^{2})$
Mode Frequency
—>生成 bdf
- File —> New —>
*.db - Menu —> Preferences —> Geometry —> 1000.0 (Millimeters) —> Apply
- File —> Import —>
*.x_t—> Apply (Display —> Smooth Shade) - Meshing —>(RHS) Mesh —> Solid —>(Main window) select solid —> Automatic Calculation —> Apply
- Properties —> Isotropic —>(RHS) Material Name —> Input properties (Elastic Modulus: 210000MPa, Shear Modulus: 83000, Density: 7.86E-09 Kg/m^3) —> Apply
- Properties —> Solid —> Propert Set Name —>(RHS) Input properties —> Mat Prop Name select gangban(Material Name) —> Select Application Region —>(Main window) select solid —> Add —> Apply
- Analysis —> Solution Type —> NORMAL MODES —> Solution Type —> Solution Parameters —> Results Output Format(XDB or OP2) —> Subcase —> Subcase Parameters —> Number of Desired Roots : 20 —> Apply Run nastran —> Get .bdf
Nastran
如何用matlab被nastran给整的明明白白 PART 1 KNOW YOUR ENEMY——.bdf文件 - 知乎 (zhihu.com)
Nastran的Python库：Welcome to pyNastran’s documentation for v1.3! — pyNastran 1.3 1.3 documentation (pynastran-git.readthedocs.io)
Debug: Nastran Error List 1. | PDF
D:\Software\Nastran\Nastran_install\bin\nastranw.exe *.bdf
卫星算例.bdf
不同结构参数生成结构特征量FR
1 | $ Elements and Element Properties for region : Shear_Panels |
- 主弹性模量$\theta_1$ 70Gpa，
- 主密度 $\theta_2$ ，密度2.7x $10^{3} kg/m^{3}$ (英文论文) or 适配器厚度 1mm(本 1)
- 中心筒厚度$\theta_3$ 2mm
- 底板厚度 $\theta_4$ 1mm
- 剪切板厚度$\theta_5$ 2mm
- 顶板厚度 $\theta_6$ 2.5mm
FEA二次开发(Python)
Ansys:
Ansys与Python：r/ANSYS —- Ansys with Python : r/ANSYS
PyAnsys — PyAnsys
Nastran:
pynastranGUI 支持对有限元模型和仿真结果的可视化，支持的模型文件格式：
Other
FE & Blender
可否指教一下blender如何渲染abaqus求解文件odb？
odb写个脚本导出obj文件，然后导进blender一张张渲染就好