QiYun

Note

Modal Testing

Posted on Edited on In
3.7k 13 mins.

Modal Testing、Experimental Modal Analysis (EMA)

模态试验实用技术 谭祥军,钱小猛译 (美国)彼得·阿维塔比莱
模态实验技术与实践 陈阳
Technical Papers | Vibrant Technology, Inc.

模态试验实用技术

实验模态分析一般理论

SDOF

系统方程

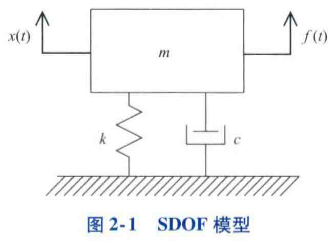
image.png|666

单自由度系统方程
$m\ddot{x}+c\dot{x}+kx=f(t)$

  • 质量是集中质量
  • 弹簧刚度线性正比于位移
  • (黏性)阻尼线性正比于速度

方程拉普拉斯域变换： $ms^2+cs+k=0$
方程的根: $P_{_{1,2}}=-\frac{c}{2m}\pm\sqrt{\left(\frac{c}{2m}\right)^2-\frac{k}{m}}$
可以重写为： $P_{_{1,2}}=-\zeta\omega_{_n}\pm\sqrt{\left(\zeta\omega_{_n}\right)^2-\omega_{_n}^2}=-\sigma\pm\mathrm{j}\omega_{_d}$

  • 阻尼因子：$\sigma=\zeta\omega_n$
  • 无阻尼固有频率：$\omega_n=\sqrt{\frac{k}{m}}$
  • 阻尼比：$\zeta=\frac{c}{c_c}$ , 当阻尼达到临界阻尼时，即$c=c_{c}, \zeta=1$
  • 临界阻尼：$c_{c}=2m\omega_n=2 \sqrt{km }$
  • 有阻尼固有频率：$\omega_d=\omega_n\sqrt{1-\zeta^2}$

无阻尼—欠阻尼—临界阻尼—过阻尼

  • $\zeta=0$，无阻尼 $\pm\mathrm{j}\omega_{_d}$
  • $0<\zeta<1$，欠阻尼 $-\sigma\pm\mathrm{j}\omega_{_d} =-\zeta w_{n}\pm jw_{n}\sqrt{1-\zeta^{2}}$
  • $\zeta=1$，临界阻尼 $-\sigma$
  • $\zeta>1$，过阻尼

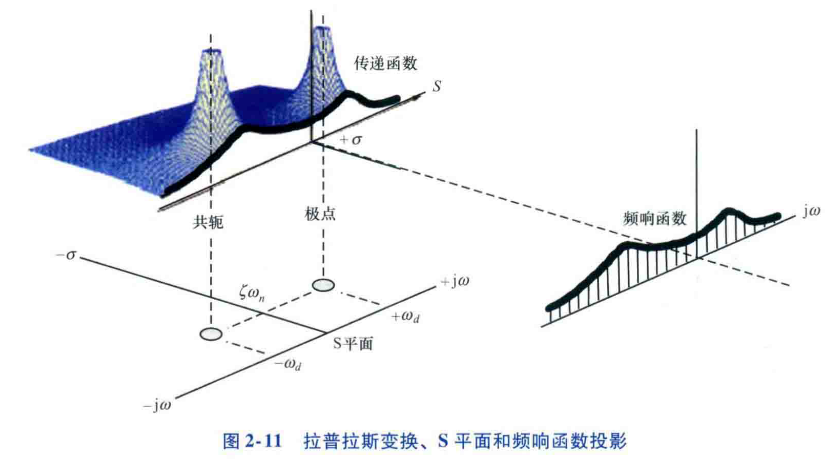
从图中可以看出，共振频率/固有频率/模态频率处的FRF由系统的阻尼决定

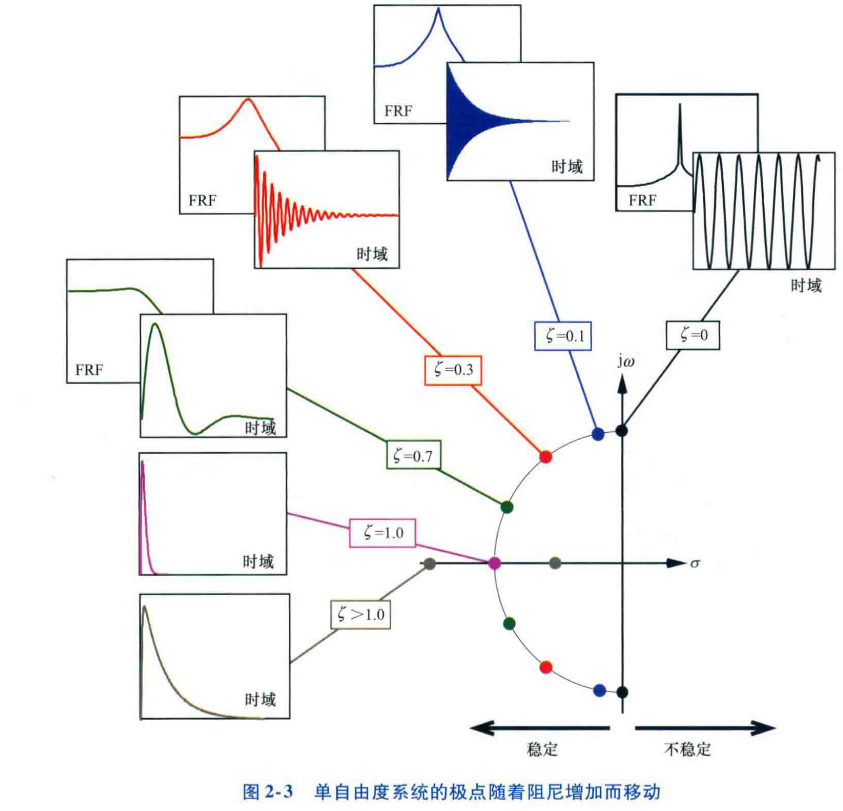
image.png|666

传递—>频响函数

SDOF系统简谐激励下的响应：

  • 位移：$x=F_0/\sqrt{\left(k-m\omega^2\right)^2+\left(c\omega\right)^2}$
  • 相位：$\varphi=\tan^{-1}\left(\frac{c\omega}{k-m\omega^2}\right)$

响应与激励之比：
$\frac{x}{\delta_{\mathrm{st}}}=\frac{1}{\sqrt{\left(1-\beta^{2}\right)^{2}+\left(2\zeta\beta\right)^{2}}}\quad\varphi=\tan^{-1}\left(\frac{2\zeta\beta}{1-\beta^{2}}\right)$，

  • $\beta=\frac{\omega}{\omega_{n}}$为激励频率与系统固有频率之比

阻尼估计

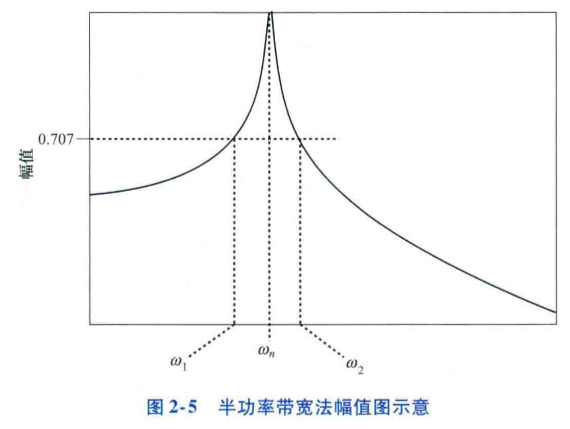
  • 半功率带宽法：阻尼与(固有频率除以半功率点对应的频率差)相关，品质因子$Q=\frac{1}{2\zeta}=\frac{\omega_n}{\omega_2-\omega_1}$ 当频率分辨率不足时，精度较差

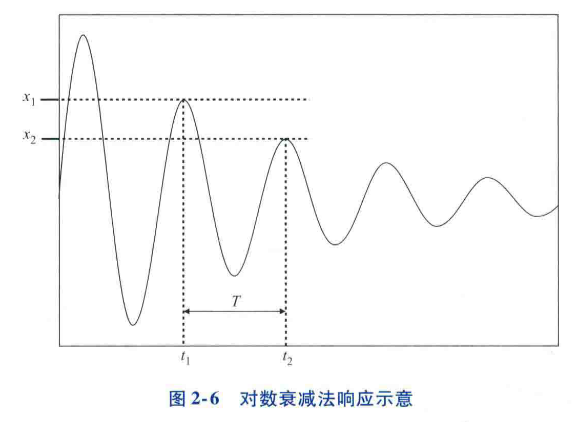
image.png|666

  • 对数衰减法：使用系统的时域响应幅值在一个或几个周期的衰减来确定阻尼，$\delta=\ln\frac{x_1}{x_2}\approx2\pi\zeta$ 时域响应只有一阶模态的情况较为少见，现实角度来看行不通

image.png|666

  • 使用模态参数估计工具(以最小二乘方式处理数据以找到感兴趣参数的最佳拟合)和模态数据来获取模态振型，进而估计模态阻尼

传递函数

运动方程拉氏变换：$(\begin{array}{c}ms^2+cs+k\end{array})x(\begin{array}{c}s\end{array})=f(\begin{array}{c}s\end{array})$
传递函数：$h\left(s\right)=\frac{1}{\left(ms^2+cs+k\right)}$
传函不同形式：

  • 多项式：$h\left(s\right)=\frac{1}{\left(ms^2+cs+k\right)}$
  • 极点-零点：$h\left(s\right)=\frac{1/m}{\left(s-p_{1}\right)\left(s-p_{1}^{*}\right)}$
  • 部分分式(实验模态常用)：
  • 复指数：$h\begin{pmatrix}t\end{pmatrix}=\frac{1}{m\omega_d}\mathrm{e}^{-\zeta\omega t}\sin\omega_dt$

什么是频响函数FRF？ - 知乎
这些FRF由留数和系统极点组成，而留数直接与模态振型相关，极点包含系统的频率和阻尼信息。
模态参数提取时用的是频响函数的幅值谱，而非实部和虚部

  • [ ] 留数： ============================= 需要复变知识 (为了估计传递函数在根位置的值)

频响函数(二维)是传递函数(三维)，沿着$s=jw$轴上的取值。频响函数的形式有：伯德图(幅值相位)、实部虚部图、奈奎斯特图(实部虚部) 虚部半功率点==实部的峰值 是否普适？
频响函数形式：

  • 多项式形式： $h\left(\mathrm{j}\omega\right)=\frac{1}{m\left(\mathrm{j}\omega\right)^2+c\left(\mathrm{j}\omega\right)+k}$
  • 极点-零点形式： $h\left(\mathrm{j}\omega\right)=\frac{1/m}{\left(\mathrm{j}\omega-p_1\right)\left(\mathrm{j}\omega-p_1^*\right)}$
  • 部分分式形式：
  • 实部-虚部形式(复数频响函数): $h(\mathrm{j}\omega)=\frac{1-\left(\frac{\omega}{\omega_n}\right)^2}{\left[1-\left(\frac{\omega}{\omega_n}\right)^2\right]^2+\left[2\zeta\left(\frac{\omega}{\omega_n}\right)\right]^2}-\mathrm{j}\frac{2\zeta\left(\frac{\omega}{\omega_n}\right)}{\left[1-\left(\frac{\omega}{\omega_n}\right)^2\right]^2+\left[2\zeta\left(\frac{\omega}{\omega_n}\right)\right]^2}$

FRF of SDOF： $H(jw)=\frac{X(jw)}{F(jw)}=\frac{1}{(k-mw^{2})+jw}$

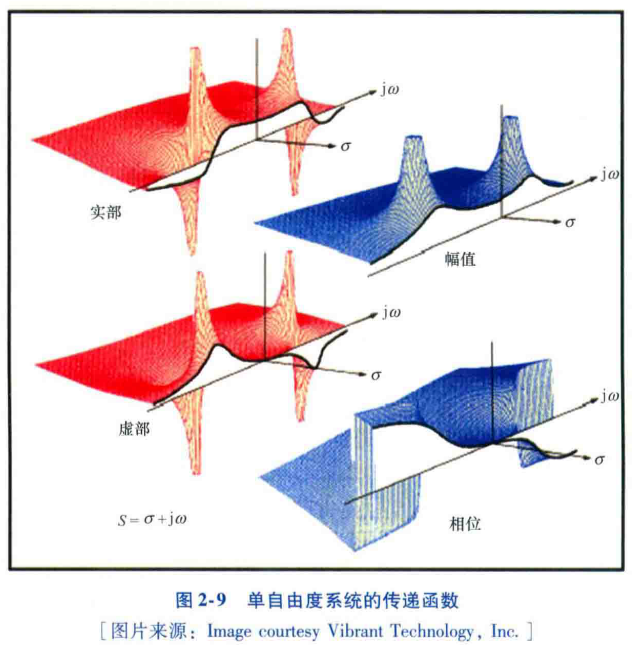
image.png|666

传递函数—频响函数—S平面之间的关系

image.png|666

为什么测试与仿真低频能对上，高频却对不上？ - 知乎

SDOF系统频响函数 $H(j\omega)=\frac{X(j\omega)}{F(j\omega)}=\frac{1}{(k-m\omega^{2})+jc\omega}$

  • 极低频区域$\omega \to 0$，$H(j\omega) \to \frac{1}{k}$ 主要由刚度控制
  • 固有频率$\omega =\sqrt{ \frac{k}{m} }$, $H(j \omega) =\frac{1}{jc\omega}$ 主要由阻尼控制
  • 极高频区域$\omega \to \infty$, $H(j \omega) \to \frac{1}{m \omega^{2}}$ 主要由质量控制

FRF的y轴值：

  • 位移，FRF称为动柔度。位移倒数，动刚度
  • 速度，FRF称为移动性。速度倒数，阻抗
  • 加速度，FRF称为惯性。加速度倒数，动质量

位移(D/F)—> 乘以$j\omega$ —> 速度(V/F) —> 乘以$j\omega$ —> 加速度(A/F) 时域求导=s域乘以s $=\sigma+j\omega$

  • 位移 $H(j\omega)=\frac{X(j\omega)}{F(j\omega)}=\frac{1}{(k-m\omega^{2})+jc\omega}$
  • 速度 $H(j\omega) * j\omega$
  • 加速度 $H(j\omega) * -\omega^{2}$

MDOF

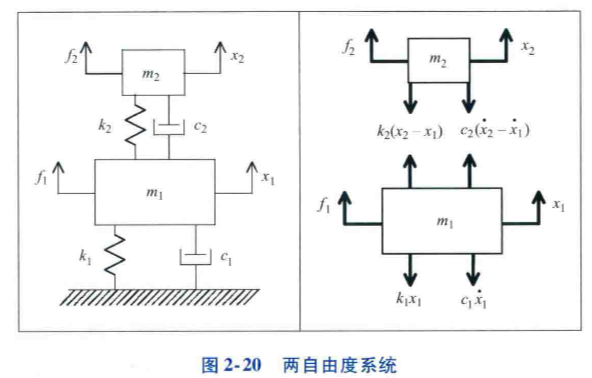
image.png|666

两自由度系统方程(矩阵形式)：

  • 其中刚度和阻尼矩阵有非对角元素，表征了质量1与 质量2之间的耦合
  • 矩阵都是对称的，规模与自由度数有关

推广到多自由度：$M\ddot{x}+C\dot{x}+Kx=F(t)$

多 自 由 度 系 统 的 振 动

特征值求解只需要质量和刚度矩阵，假设阻尼矩阵为0或者正比例于质量/刚度矩阵(关注的是系统的自由振动模式（即没有外部强迫力或阻尼效应的情况下，系统如何振动)，阻尼的存在使得系统的特征值变为复数，表示系统在振动过程中的衰减特性。
方程 $(K-\lambda M)\mathrm{x}=0$ —> $\mid K\mathrm{-}\omega^2M\mid =0$ 方程的解$\omega$即为特征频率 （方程的解为频响函数的零点） 对应的特征向量$\mathrm{x}$即为振动模式/模态振型。
求解方法：

  • 直接法：Jacobi、Givens、Householder
  • 间接法：(大型有限元模型) Subspace Iteration、Simultaneous Vector Iteration、Lanczos

实践

Modal Testing: A Practical Guide

双击影响

测量的FRFs噪声很大

rtaImage (669×410)

rtaImage (672×409)

Mode Frequency

模态空间│不同的模态指示函数有什么区别？_模态试验__汽车测试网

SUM —和函数 所测的全部频响函数之和
MIF —模态指示函数 尽管SUM很有用，但是它并不能很清晰地区分密集模态，为了更好地进行区分，提出了最初的模态指示函数（MIF）。从本质上讲，MIF的数学公式就是频响函数的实部除以频响函数的幅值。由于实部在共振区快速穿过零点，MIF在某阶模态附近会发生剧变，共振时频响函数的实部为零。因此，MIF将在某阶模态附近将下降至最小值。
MMIF —多变量模态指示函数 针对多参考点频响函数数据的MIF的扩展。MMIF函数同样遵循单个MIF函数的基本特征，它的最大优点就是多参考点数据会有多个MIF（每个参考点各有一个），可以有效识别出重根
CMIF —复模态指示函数
SD stabilization diagram —稳态图 基本原理是如果极点是系统的全局特征，那么从模态阶数不断增长的数学模型中提取的极点将随着模态阶数的增加而重复出现

MAC

Modal Assurance Criterion (MAC)

Modal Assurance Criterion (MAC) is used to determine the similarity of two mode shapes.

判断是否有近似的模态，防止设置的测量点不够，而无法获取正确的振型

rtaImage (704×365)

rtaImage (704×365)

rtaImage (831×351)

其他基本概念

实验模态分析初步
模态分析理论与试验基础

功率谱密度

SunnyFHY
什么是功率谱密度？为什么它很重要？ 功率谱密度 (PSD) 是信号在不同频率上的功率分布

要区分功率谱和能量谱，首先要清楚两种不同类型的信号：功率有限信号和能量有限信号。

  • 信号的归一化能量（简称信号的能量）定义为信号电压或电流f(t)加到1Ω电阻上所消耗的能量
  • 信号的平均功率（简称信号的功率）是指信号电压或电流在1Ω电阻上所消耗的功率

一般来说，周期信号和随机信号是功率信号，而非周期的确定信号是能量信号。

  • 能量谱是信号幅度谱的模的平方，其量纲是焦/赫
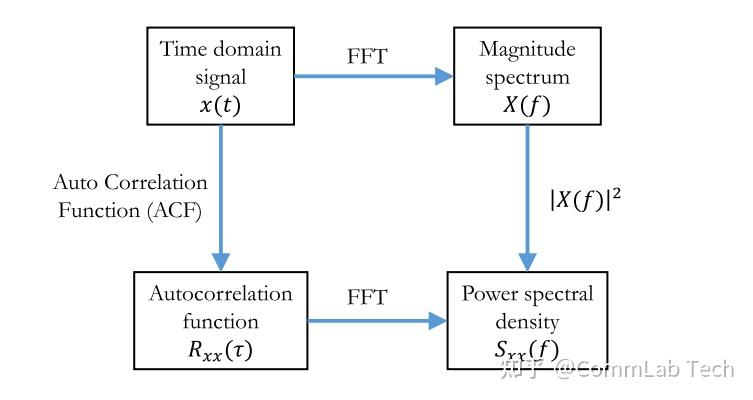
  • 功率谱是信号自相关函数的傅里叶变换

今天，从头捋一捋功率谱和能量谱 - stayHungry的文章 - 知乎

电流信号$f(t)$作用在$1 \Omega$ 电阻上消耗的能量： $E=\int_{-\infty}^\infty\left|f(t)\right|^2\mathrm{d}t$
平均功率：$P=\lim_{T\to\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\left|f(t)\right|^2\mathrm{d}t$

  • 如果 E 是一个非无穷大也非0的常数，那么 f(t) 就定义为能量有限信号，简称能量信号。显然，能量信号的平均功率 P 为0；
  • 如果 P 是一个非无穷大也非0的常数，比如 f(t) 为周期信号或者统计量满足某一分布的随机信号时，那么 f(t) 就定义为功率有限信号，简称功率信号。显然，功率信号的能量 E 为无穷大。

相关函数：
能量信号

信号$f(t)$的自相关函数：$R(\tau)=\int_{-\infty}^\infty f(t)f(t-\tau)dt=\int_{-\infty}^\infty f(t+\tau)f(t)dt$

  • $R(\tau)=R(-\tau)$ 自相关函数 R(τ) 是时移 τ 的偶函数。

$f_2(t)$和$f_1(t)$ 的互相关函数：$R_{12}(\tau)=\int_{-\infty}^\infty f_1(t)f_2(t-\tau)dt=\int_{-\infty}^\infty f_1(t+\tau)f_2(t)dt$

$f_2(t)$和$f_1(t)$ 的互相关函数： $R_{21}(\tau)=\int_{-\infty}^\infty f_1(t-\tau)f_2(t)dt=\int_{-\infty}^\infty f_1(t)f_2(t+\tau)dt$

功率信号

自相关
$R(\tau)=\lim_{T\to\infty}\left[\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)f(t-\tau)\mathrm{d}t\right]$

功率信号的自相关函数与功率谱是一对傅里叶变换.

互相关
$\left.\left\{\begin{array}{l}R_{12}(\tau)=\lim_{T\to\infty}\left[\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_1(t)f_2(t-\tau)\mathrm{d}t\right]\\R_{21}(\tau)=\lim_{T\to\infty}\left[\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f_1(t-\tau)f_2(t)\mathrm{d}t\right]\end{array}\right.\right.$

类似卷积

如何理解随机振动的功率谱密度？ - J Pan的文章 - 知乎 一个信号的功率密度谱，就是其自相关函数的傅里叶变换。

自相关函数

$R_x(\tau)=\lim_{T\to\infty}\frac{1}{T}\int_{-\infty}^{+\infty}x(t)x(t+\tau)dt$

随机过程 x(t) 的自相关函数定义为在时刻 t 和时刻 t+τ 的随机变量乘积的平均值，反映了随机信号本身在不同时刻的相互关系

对于平稳随机信号，自相关函数将信号的平均功率向 τ=0 这一点集中， τ≠0 时自相关函数快速衰减为零

自相关函数能够检测出信号内部蕴藏的周期组分，而过滤掉了周期组分的相位信息。

帕斯瓦定理：信号的能量在时域和频域是一样的
$\int_{-\infty}^{+\infty}|x(t)|^2dt=\frac{1}{2\pi}\int_{-\infty}^{+\infty}|F_x(\omega)|^2d\omega=\int_{-\infty}^{+\infty}|F_x(2\pi f)|^2df$

因此将自相关函数从时域通过FT到频域，即为功率密度谱：
$S_x(f)=\int_{-\infty}^{+\infty}R_x(\tau)e^{-i2\pi f\tau}d\tau$
$R_x(\tau)=\int_a^bS_x(f)e^{i2\pi f\tau}df$

功率被定义成幅值的平方的时间平均分量，而这个过程，也可以看成是去除频域谐波分量的相位信息的过程，因为本质来说，一个简谐信号的相位是不影响其功率的。而自相关函数，也具有去除信号相位的功能

相干函数

数字信号处理基础-12 传递函数与相干（coherence）函数 - XYZ图像工作室的文章 - 知乎

相干函数（Coherence Function），它对评测传递函数结果的可靠性非常重要。

输出信号：$y(t)=v(t)+n(t)……(1)$， $v(t)$是输入信号$x(t)$经过系统后得到的输出信号，无法测量，$n(t)$为噪声

由传递函数, 仅由输入信号x(t) 产生的输出信号 v(t) 功率谱的表达式为：$G_{vv}(f)=\left|H(f)\right|^2G_{xx}(f)$
相干函数 $\gamma^2(f)=\frac{G_{vv}(f)}{G_{yy}(f)}=\frac{\left|H(f)\right|^2G_{xx}(f)}{G_{yy}(f)}=\frac{\left|G_{xy}(f)\right|^2}{G_{xx}(f)G_{yy}(f)}$

相干函数，表示基于输入信号产生的功率在总输出功率中的占比，相干函数用于评估传递函数结果的可靠性。一般情况下，当相干函数大于等于0.9时，就可以认为得到的传递函数的结果比较可靠。

信号处理方法 - 声振论坛 - 振动,动力学,声学,信号处理,故障诊断 - Powered by Discuz!

相干性是频率的函数关系，它表示有多少输出是由FRF中的输入引起的。它可以作为FRF质量的指标。它评估从测量到重复相同测量的FRF的一致性。
多次敲击的输入对输出的影响是否一致

v2-cd550e325a2cbb8381a4dbf95b9c6e4e_1440w.jpg (753×400)

倍频程扫描速率

振动试验中倍频程扫描速率这个参数的意义_哔哩哔哩_bilibili

扫描速率：$n=2 (oct/min)$ 2倍频程每分钟
扫频范围：4~100Hz

则扫频耗费时间为：
$\Delta t= \frac{60}{n\ln2} \ln(\frac{f_{2}}{f_{1}})$

Welcome to my other publishing channels