QiYun

Note

Sampling Method

Posted on In
2.6k 9 mins.

Sampling Method

Sampling

如何在不知道目标概率密度函数的情况下，抽取所需数量的样本，使得这些样本符合目标概率密度函数。这个问题简称为抽样

Finite Element Model Updating in Bridge Structures Using Kriging Model and Latin Hypercube Sampling Method - Wu - 2018 - Advances in Civil Engineering - Wiley Online Library 不同采样方法的讨论(simple random sampling (SRS), stratified sampling method, cluster sampling method, and systematic sampling) Latin Hypercube Sampling 属于 =分层采样
It’s all about Sampling - 子淳的博客 | Just Me

Monte Carlo

一文看懂蒙特卡洛采样方法 - 知乎 (zhihu.com)
简明例析蒙特卡洛（Monte Carlo）抽样方法 - 知乎 (zhihu.com)
走进贝叶斯统计（四）—— 蒙特卡洛方法 - 知乎
逆变换采样和拒绝采样 - barwe - 博客园 (cnblogs.com)
Monte Carlo method - Wikipedia
【数之道 22】巧妙使用”接受-拒绝”方法，玩转复杂分布抽样 - YouTube

MC Sampling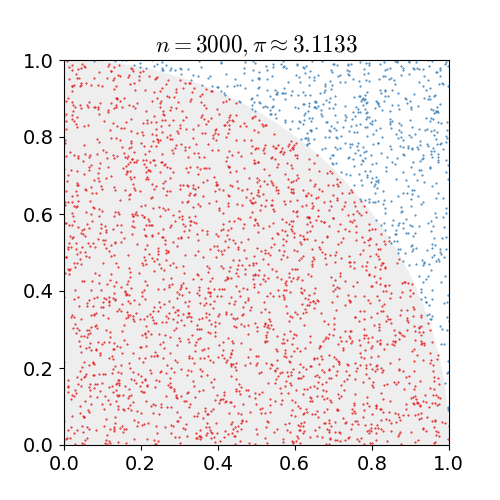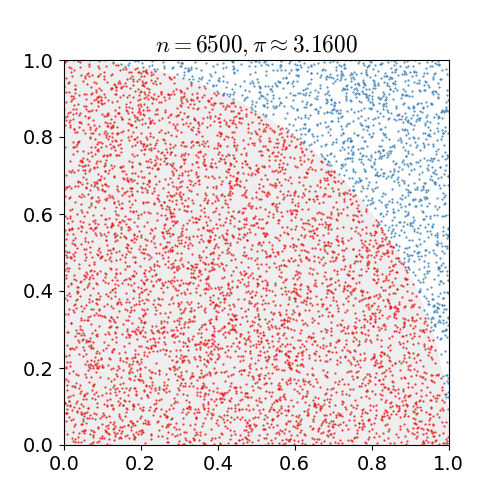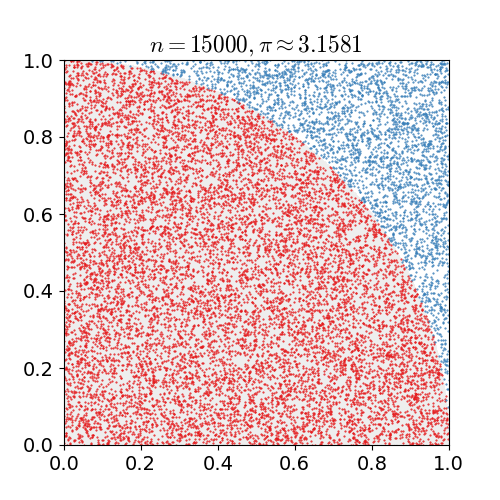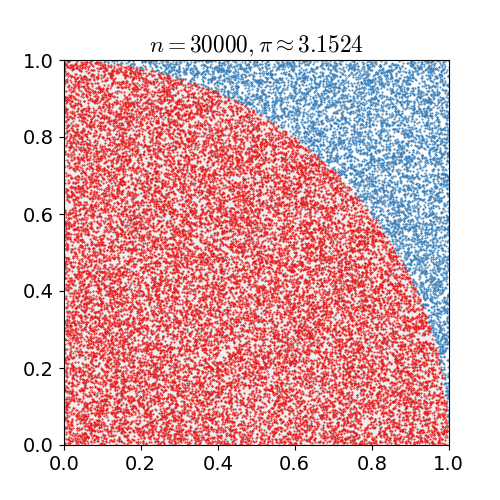
v2-eb0945aa2185df958f4568e58300e77a_1440w.gif|222

对某一种概率分布p(x)进行蒙特卡洛采样的方法主要分为直接采样、拒绝采样与重要性采样三种:

  • Naive Method
    • 根据概率分布进行采样。对一个已知概率密度函数与累积概率密度函数的概率分布，我们可以直接从累积分布函数（cdf）进行采样（类似逆变换采样）
  • Acceptance-Rejection Method
    • 逆变换采样虽然简单有效，但是当累积分布函数或者反函数难求时却难以实施，可使用MC的接受拒绝采样
    • 对于累积分布函数未知的分布，我们可以采用接受-拒绝采样。如下图所示，p(z)是我们希望采样的分布，q(z)是我们提议的分布(proposal distribution)，令kq(z)>p(z)，我们首先在kq(z)中按照直接采样的方法采样粒子，接下来判断这个粒子落在途中什么区域，对于落在灰色区域的粒子予以拒绝，落在红线下的粒子接受，最终得到符合p(z)的N个粒子
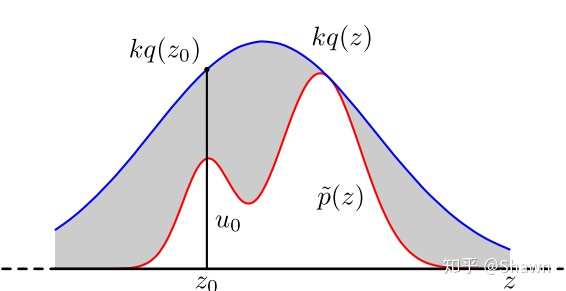
    • image.png|333
    • 数学推导：
      • image.png|500
      1. 从 $f_r(x)$ 进行一次采样 $x_i$
      2. 计算 $x_i$ 的 接受概率 $\alpha$（Acceptance Probability）:$\alpha=\frac{f\left(x_i\right)}{f_r\left(x_i\right)}$
      3. 从 (0,1) 均匀分布中进行一次采样 u
      4. 如果 $\alpha$≥u，接受 $x_i$ 作为一个来自 f(x) 的采样；否则，重复第1步
1
2
3
4
5
6
7
8
9
10
N=1000 #number of samples needed
i = 1
X = np.array([])
while i < N:
    u = np.random.rand()
    x = (np.random.rand()-0.5)*8
    res = u < eval(x)/ref(x)
    if res:
        X = np.hstack((X,x[res])) #accept
        ++i
  • Importance Sampling
    • 接受拒绝采样完美的解决了累积分布函数不可求时的采样问题。但是接受拒绝采样非常依赖于提议分布(proposal distribution)的选择，如果提议分布选择的不好，可能采样时间很长却获得很少满足分布的粒子。
    • $E_{p(x)}[f(x)]=\int_a^bf(x)\frac{p(x)}{q(x)}q(x)dx=E_{q(x)}[f(x)\frac{p(x)}{q(x)}]$
    • 我们从提议分布q(x)中采样大量粒子$x_1,x_2,…,x_n$，每个粒子的权重是 $\frac{p(x_i)}{q(x_i)}$，通过加权平均的方式可以计算出期望:
    • $E_{p(x)}[f(x)]=\frac{1}{N}\sum f(x_i)\frac{p(x_i)}{q(x_i)}$
      • q提议的分布，p希望的采样分布
1
2
3
4
5
6
7
8
9
10
11
12
N=100000
M=5000
x = (np.random.rand(N)-0.5)*16
w_x = eval(x)/ref(x)
w_x = w_x/sum(w_x)
w_xc = np.cumsum(w_x) #accumulate

X=np.array([])
for i in range(M):
    u = np.random.rand()
    X = np.hstack((X,x[w_xc>u][0])) # 其中，w_xc是对归一化后的权重计算的累计分布概率。每次取最终样本时，都会先随机一个(0,1)之间的随机数，并使用这个累计分布概率做选择。样本的权重越大，被选中的概率就越高。

分层采样

分层抖动采样

Physically Based Rendering：采样和重建（二） | YangWC’s Blog

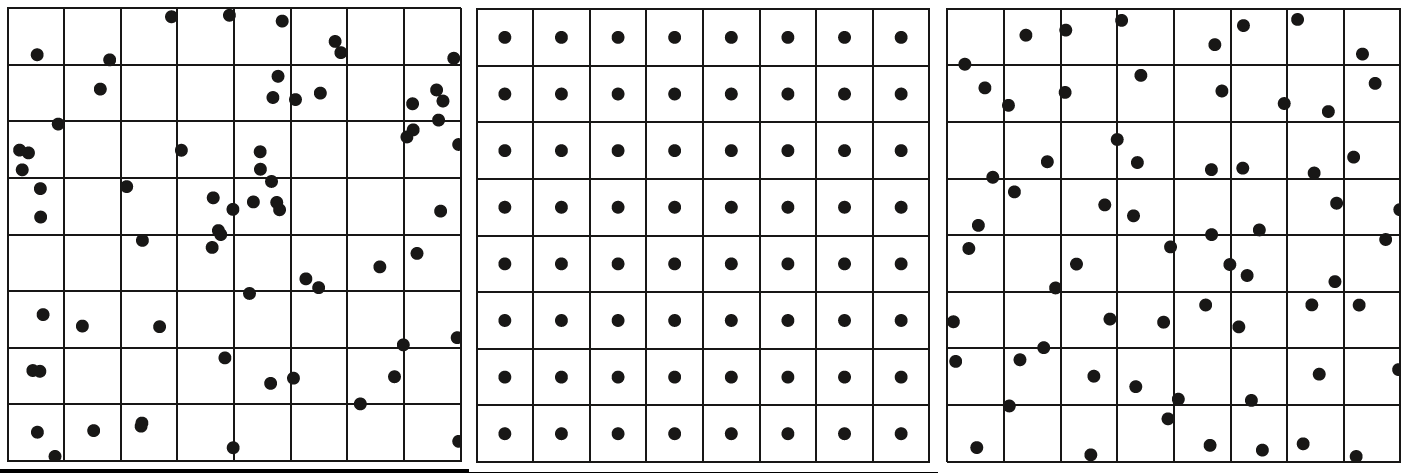
image.png|666

  • 随机采样
  • 分层均匀采样
  • 分层抖动采样。理想的分层抖动采样很容易陷入维数灾难，因此有人提出了高维转低维采样+随机串联(or随机配对)的方法

Latin Hypercube Sampling

  1. 将每个维度的区间划分为m个不重叠的区间，每个区间概率相等（取均匀分布，区间大小应相等）
  2. 从均匀分布中随机采样，每个维度的每个间隔中的一个点
  3. 将每个维度的点随机配对（相同可能的组合）

相较于Simple Random Sampling，LHS的方法更加分散，且不存在聚类效应

MCMC

(Markov Chain Monte Carlo)

Blog:

马尔可夫链蒙特卡罗算法（MCMC） - 知乎
动画 The Markov-chain Monte Carlo Interactive Gallery | 代码 Javascript demos
MCMC MCMC: A (very) Beginnner’s Guide

Paper:

An effective introduction to the Markov Chain Monte Carlo method For physics
A Conceptual Introduction to Markov Chain Monte Carlo Methods
Markov Chain Monte Carlo in Practice | W.R. Gilks, S. Richardson, Davi MCMC需要小心地初始化，早期阶段需要warm-up time

M-H采样

走进贝叶斯统计（五）—— Metropolis-Hasting 算法 - 知乎

Gibbs采样

走进贝叶斯统计（六）—— 吉布斯抽样 （Gibbs Sampling） - 知乎

TMCMC

Transitional Markov Chain Monte Carlo Method for Bayesian Model Updating, Model Class Selection, and Model Averaging

拉丁超立方采样(Latin hypercube sampling, LHS)

拉丁超立方采样(Latin hypercube sampling, LHS)及蒙特卡洛模拟简介 - 知乎

拉丁超立方采样先把样本空间分层，在此问题下要分为5层，于是便有了 [1,20],[21,40],[41,60],[61,80],[81,100] 共5个样本空间，在各样本空间内进行随机抽样，然后再打乱顺序，得到结果。这样就结束了~

可以看出拉丁超立方采样分为了三步——分层、采样、乱序。

Hammersley sampling

Hammersley采样是一种确定性的、低差异度的采样方法，属于准蒙特卡洛（Quasi-Monte Carlo）方法的范畴。 与依赖伪随机数生成器的传统蒙特卡洛方法不同，Hammersley采样使用一种基于Hammersley点集的准随机数生成器，旨在在一个单位超立方体中生成高度均匀的样本点。 这种均匀分布的特性使得Hammersley采样在许多应用中比随机采样或其他采样方法（如拉丁超立方采样）更有效率。

Hammersley采样如何工作？

Hammersley采样通过一种被称为“激进逆”（radical inverse）的构造方法生成样本点，该方法与哈尔顿序列（Halton sequence）密切相关。 一个d维的Hammersley点集是这样生成的：

  • 第一维：对于要生成的N个样本点，第一维的坐标是简单地将区间[0, 1)均匀划分为N份，即 i/N，其中 i 从0到N-1。
  • 其他维度：对于剩下的d-1个维度，其坐标是通过“激进逆”函数，并使用d-1个互为质数的基数（通常是最小的d-1个素数，如2, 3, 5, …）来生成的。

激进逆函数 的基本思想是：对于一个整数 i 和一个基数 p，首先将 i 表示为p进制数，然后将这个p进制数的各位数字颠倒顺序，并将其放在小数点后，从而得到一个在[0, 1)区间内的数。

例如，要生成一个二维的Hammersley点集，我们会：

  1. 第一维：使用均匀间隔的点：0/N, 1/N, 2/N, …
  2. 第二维：使用基数为2的激进逆（也称为Van der Corput序列）。

这种构造方法保证了点集在整个空间中分布得非常均匀，避免了随机采样中可能出现的点簇和空白区域。

主要特点和优势
  • 高均匀性和低差异度：Hammersley点集被设计为在k维超立方体上实现最优的点布局。 这种优良的均匀分布特性意味着与随机采样相比，它能用更少的样本点来获得对输出统计数据（如均值）的可靠估计。
  • 高效率：在计算不确定性时，Hammersley采样可以将所需的样本数量减少2到100倍。
  • 确定性：与随机采样不同，Hammersley序列是完全确定的，不涉及随机数生成。
  • 优于拉丁超立方采样（LHS）：虽然LHS在每个维度上都保证了均匀分布，但Hammersley在整个k维超立方体上提供了更好的整体均匀性。
应用领域

Hammersley采样及其相关的低差异序列被广泛应用于需要高效数值积分和空间采样的领域，例如：

  • 计算机图形学：在光线追踪和辐射度算法中，用于生成均匀的采样模式以减少图像噪点。
  • 优化与不确定性分析：在需要探索参数空间的设计实验（DOE）和不确定性量化中，Hammersley采样是一种高效的选择。
  • 金融建模：用于准蒙特卡洛积分，以评估复杂的金融衍生品。
局限性

尽管Hammersley采样非常有效，但它也有一些局限性：

  • 维度限制：当维度增加时（通常超过10维），Hammersley序列的性能会下降，点之间可能会出现不希望的相关性。 在更高维度的问题中，像Sobol序列这样的其他低差异序列可能表现更好。
  • 固定样本数：标准的Hammersley点集需要预先知道总样本数N。 如果需要增量式地添加样本，哈尔顿序列是更好的选择，因为哈尔顿序列的所有前缀都保持了良好的分布特性。

总而言之，Hammersley采样是一种强大而高效的确定性采样技术，特别适用于低维空间中的均匀采样。它通过生成低差异度的点集，能够在保证精度的同时，显著减少蒙特卡洛模拟所需的样本数量。低差异度的点集，能够在保证精度的同时，显著减少蒙特卡洛模拟所需的样本数量。

Langevin Monte Carlo(LMC)

什么是diffusion model? 它为什么好用？ - Zephyr的回答 - 知乎

$\mathbf{x}_{t+1}=\mathbf{x}_t+a\nabla\log Q(\mathbf{x}_t)+b\boldsymbol{\eta}_{t+1},$

  • a>0 is a hyperparameter defining the step size for the gradient-based walks
  • b>0 is a hyperparameter defining the step size for the random walk $\boldsymbol{\eta}_{t\boldsymbol{+}1}\boldsymbol{\sim}\mathcal{N}(0,\mathbf{1})$
  • 采样是局部的，因此采样的开销很小
  • log的作用应该是把乘除转换成加减, eg: $w_i=\frac{p(x_i)}{q(x_i)}, \log w_i=\log p(x_i)-\log q(x_i)$

Hamiltonian Monte Carlo(HMC)

Welcome to my other publishing channels