学习深度学习过程中的一些基础知识
| DL | 修仙.炼丹 | example |
|---|---|---|
| 框架 | 丹炉 | PyTorch |
| 网络 | 丹方.灵阵 | CNN |
| 数据集 | 灵材 | MNIST |
| GPU | 真火 | NVIDIA |
| 模型 | 成丹 | .ckpt |
技巧
归一化
输入数据的归一化:
当输入的数据为多个变量时,如果某个变量的变化远大于其他变量的变化,则会出现大数吃小数问题,网络会按着变化大的变量(对其最为敏感)来预测。
Model
CNN(Spatial)
1 | """ |
maxpooling时,会向下取整,丢弃掉多余的行/列
例如251,一次maxpooling(kernel=2,stride=2),则变成125,第二次则变成了62
nn.ConvTranspose2d | PyTorch function fully discussed | stride, padding, output_padding, dilation - YouTube
ConvTranspose2d 的输出尺寸公式:
H_out = (H_in - 1) stride_h - 2 padding_h + kernel_size_h + output_padding_h
W_out = (W_in - 1) stride_w - 2 padding_w + kernel_size_w + output_padding_w
UCNN
单向卷积
BCNN
kumar-shridhar/PyTorch-BayesianCNN: Bayesian Convolutional Neural Network with Variational Inference based on Bayes by Backprop in PyTorch.
Bayesian neural network introduction - 知乎
重参数 (Reparameterization)-CSDN博客 漫谈重参数:从正态分布到Gumbel Softmax - 科学空间|Scientific Spaces
初始化的权重参数用高斯先验分布表示:$p(w^{(i)})=\prod_i\mathcal{N}(w_i|0,\sigma_p^2)$,训练的过程就是根据权重先验和数据集来获得权重参数的后验分布:$p(w|\mathcal{D})=\frac{p(\mathcal{D}|w)p(w)}{p(\mathcal{D})}$
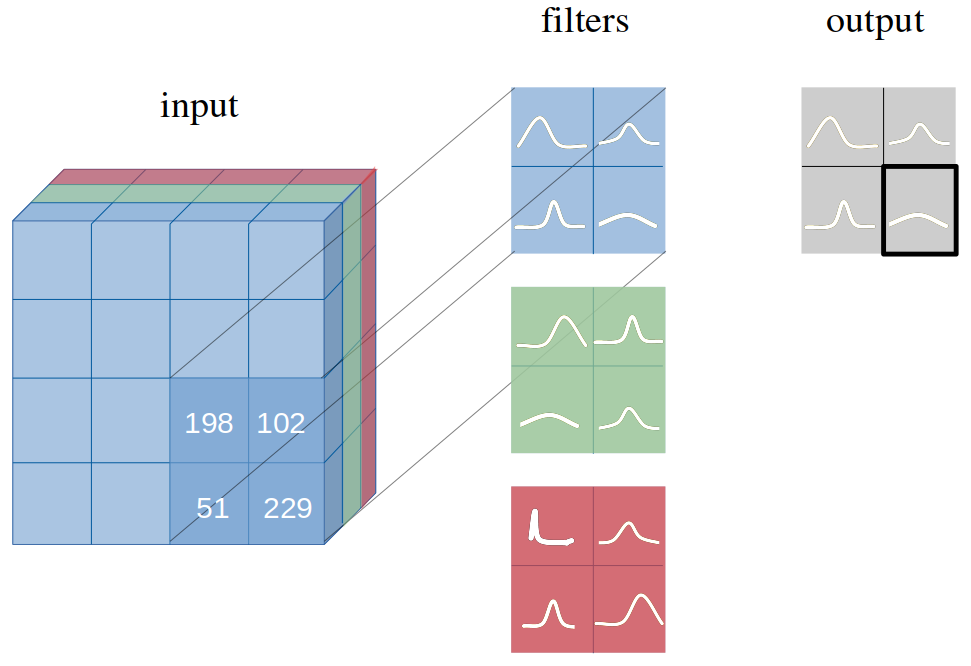
具体流程:对数据使用两个卷积核进行操作,得到两个输出的feature map,分别作为真实输出的均值和标准差。随后使用高斯分布从两个feature map中采样,得到该层feature map的激活值,作为下一层的输入。
激活值$\begin{aligned}b_j=A_i\mu_i+\epsilon_j\odot\sqrt{A_i^2(\alpha_i\odot\mu_i^2)}\end{aligned}$ (Reparameterization)
- 为了解决从分布中采样不可微的问题,使用基于重参数化(Reparameterization)的反向传播方法来估计梯度
VGG16
VGG16学习笔记 | 韩鼎の个人网站 (deanhan.com)
ResNet
ResNet中的BasicBlock与bottleneck-CSDN博客
RNN(Temporal)
相比一般的神经网络来说,他能够处理序列变化的数据
LSTM
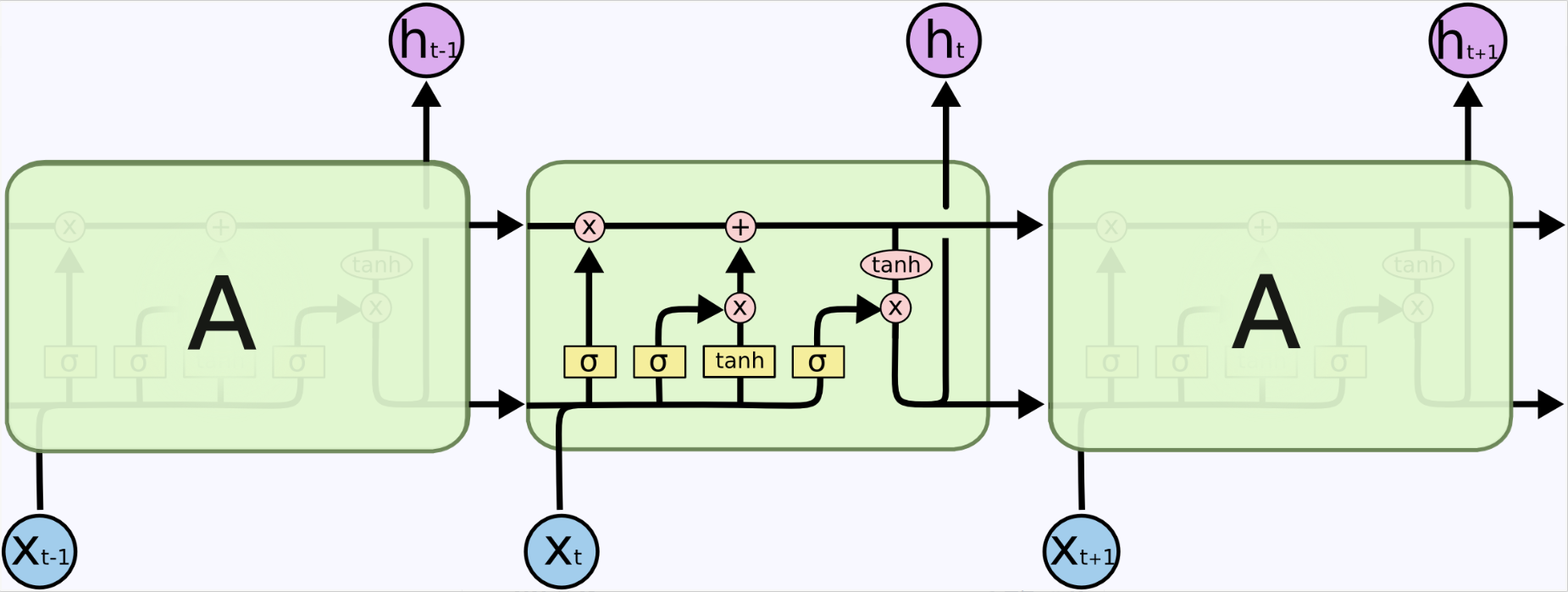
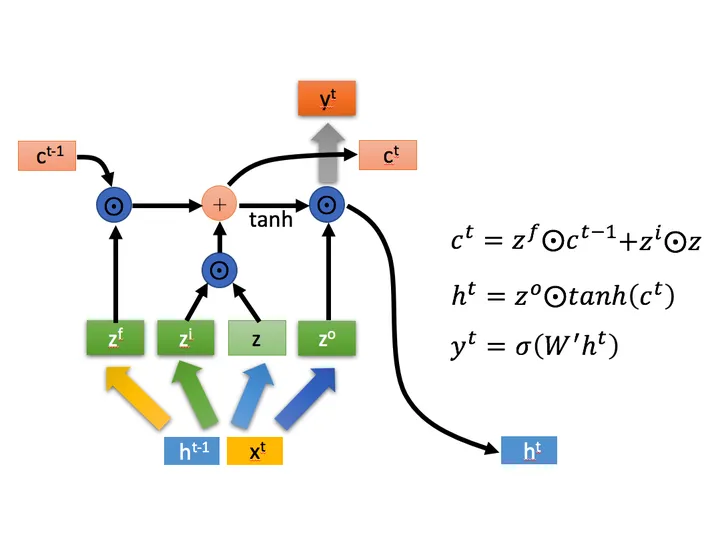
1
2
3
4
5
6self.rnn = nn.LSTM(input_size=in_dim,
hidden_size=hidden_dim,
num_layers=num_layers,
batch_first=batch_first,
bidirectional=bidirectional,
dropout=self.dropout)
LSTM — PyTorch 2.8 documentation
PyTorch 中 LSTM 的 output、h_n 和 c_n 之间的关系_lstm 最终output h c有什么关系-CSDN博客
batch_first,设为True,让Batch size为第一维
bidirectional,是否双向,默认False
输入(B, Seq, feature)的数据,self.rnn输出:
- output: (B, seq, hidden_size)
- h_n:(n_layers, B, hidden_size)
- c_n: (n_layers, B, hidden_size)
可以直接把h_n[-1],即最后一层输出output的最后一个数seq=-1作为输出
也可以把output直接作为输出,然后通过线性层继续提取特征
U-Net
U-Net (labml.ai)
anxingle/UNet-pytorch: medical image semantic segmentation
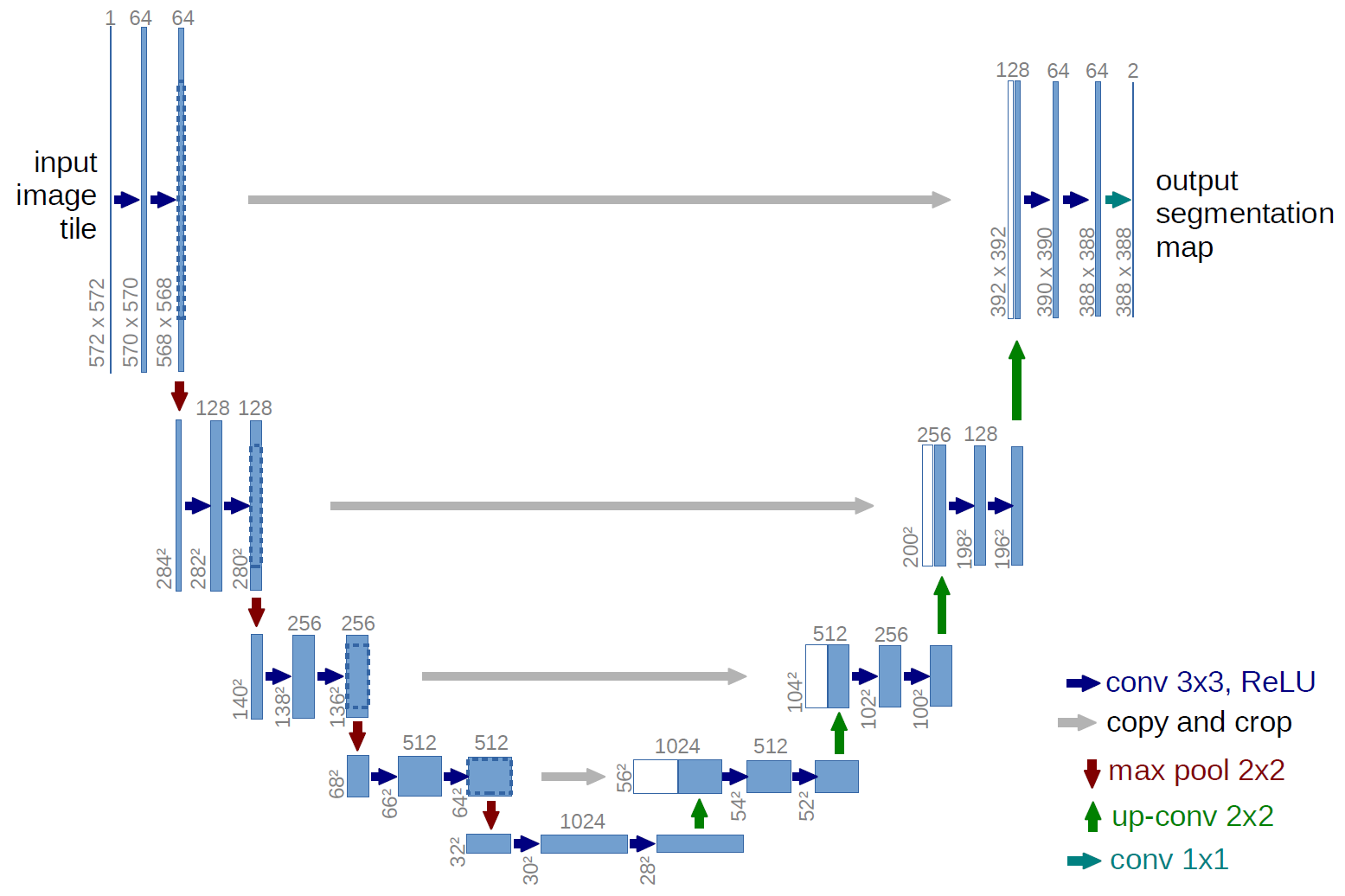
图像分割
Generate Model
概览:VAE, GAN, Flow Model 和 Diffusion 的关系_vae gan diffusion 知乎-CSDN博客
GAN
GAN在结构上受博弈论中的二人零和博弈 (即二人的利益之和为零,一方的所得正是另一方的所失)的启发,训练过程:
- 训练判别器:首先我们随机初始化生成器 G,并输入一组随机向量(Randomly sample a vactor),以此产生一些图片,并把这些图片标注成 0(假图片)。同时把来自真实分布中的图片标注成 1(真图片)。两者同时丢进判别器 D 中,以此来训练判别器 D 。实现当输入是真图片的时候,判别器给出接近于 1 的分数,而输入假图片的时候,判别器给出接近于 0 的低分。
- 训练生成器:对于生成网络,目的是生成尽可能逼真的样本。所以在训练生成网络的时候,我们需要联合判别网络一起才能达到训练的目的。也就是说,通过将两者串接的方式来产生误差从而得以训练生成网络。步骤是:我们通过随机向量(噪声数据)经由生成网络产生一组假数据,并将这些假数据都标记为 1 。然后将这些假数据输入到判别网路里边,火眼金睛的判别器肯定会发现这些标榜为真实数据(标记为1)的输入都是假数据(给出低分),这样就产生了误差。在训练这个串接的网络的时候,一个很重要的操作就是不要让判别网络的参数发生变化,只是把误差一直传,传到生成网络那块后更新生成网络的参数。这样就完成了生成网络的训练了。
已知真实的分布$p_{data}(x)$,如何找到最合适的参数z,来使得生成的$p_{model}(x;z)$与真实分布之间的差异最小——极大似然估计:
- $\theta_{ML}=arg\operatorname{\max}_{\theta}p_{model}(X;\theta)=arg\operatorname{max}_{\theta}\prod_{i=1}^mp_{model}(x^{(i)};\theta)$
- $\theta_{ML}=arg\underset{\theta}{\operatorname*{max}}\sum_{i=1}^mlog\left.p_{model}(x^{(i)};\theta)\right.$ 通过log将累乘变成累加
- $\theta_{ML} = arg\max_{\theta} E_{x \sim \hat{p}_{data}} log p_{model}(x;\theta)$ 由于缩放代价函数不会影响求导和求argmax,因此除以m来将求和变成期望,当m—>$\infty$ 时,经验分布就会是真实数据的分布$\hat{p}_{data}\to p_{data}(x)$
通过$p_{model(x)}$与$p_{data}(x)$之间的差异衡量,来训练G和D:
- $D^{*}=arg\max_{D}V(G,D)$ 生成器固定,判别器D判断的越好,V=1+1越大,D越差,V=0+0越小
- $G^{*}=arg\min_{G}\max_{D}V(G,D)$ 判别器固定,生成器G生成的越好,V=1+0越小
VAE
AE:PyTorch-Tutorial/tutorial-contents/404_autoencoder.py at master · MorvanZhou/PyTorch-Tutorial
VAE:相较于AE的离散潜在空间,VAE的目标是使得潜在空间连续(正态分布),这样才能从任意潜在空间样本生成目标数据
$D_{KL}(P||Q)=\int p(x)\log\left(\frac{p(x)}{q(x)}\right)dx\mathrm{。}$ $D_{KL}(P||Q)=\log\frac{\sigma_{2}}{\sigma_{1}}+\frac{\sigma_{1}^{2}+(\mu_{1}-\mu_{2})^{2}}{2\sigma_{2}^{2}}-\frac{1}{2}$
$Loss_{recon}=-\mathbb{E}_{q(\mathbf{z}|\mathbf{x})}\left[\log p(\mathbf{x}|\mathbf{z})\right]$
【生成式AI】Diffusion Model 原理剖析 (2/4) (optional) - YouTube
生成模型共同目标: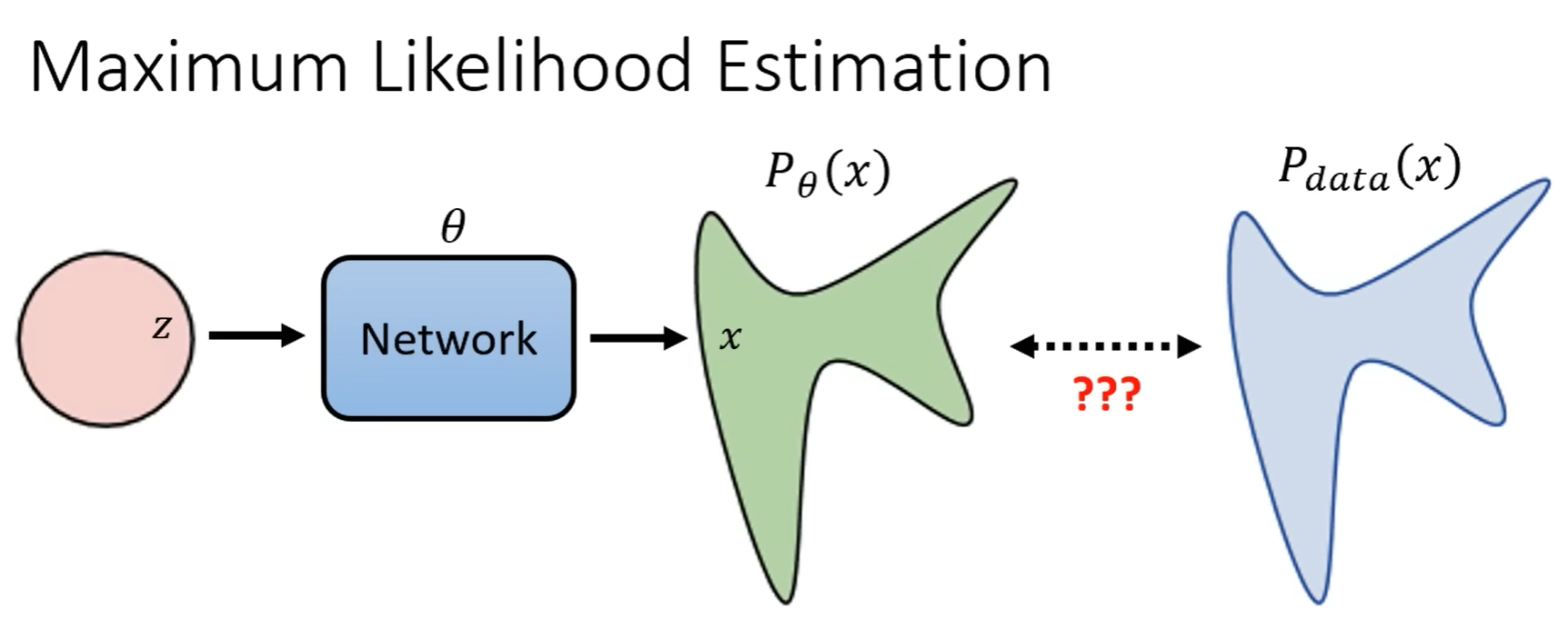
如何优化:
Maximum Likelihood == Minimize KL Divergence
最大化 $P_{\theta}(x)$ 分布中从 $P_{data}(x)$ 采样出来的 $x_{i},…, x_{m}$ 的概率,相当于最小化 $P_{\theta}(x)$ 与 $P_{data}(x)$ 之间的差异
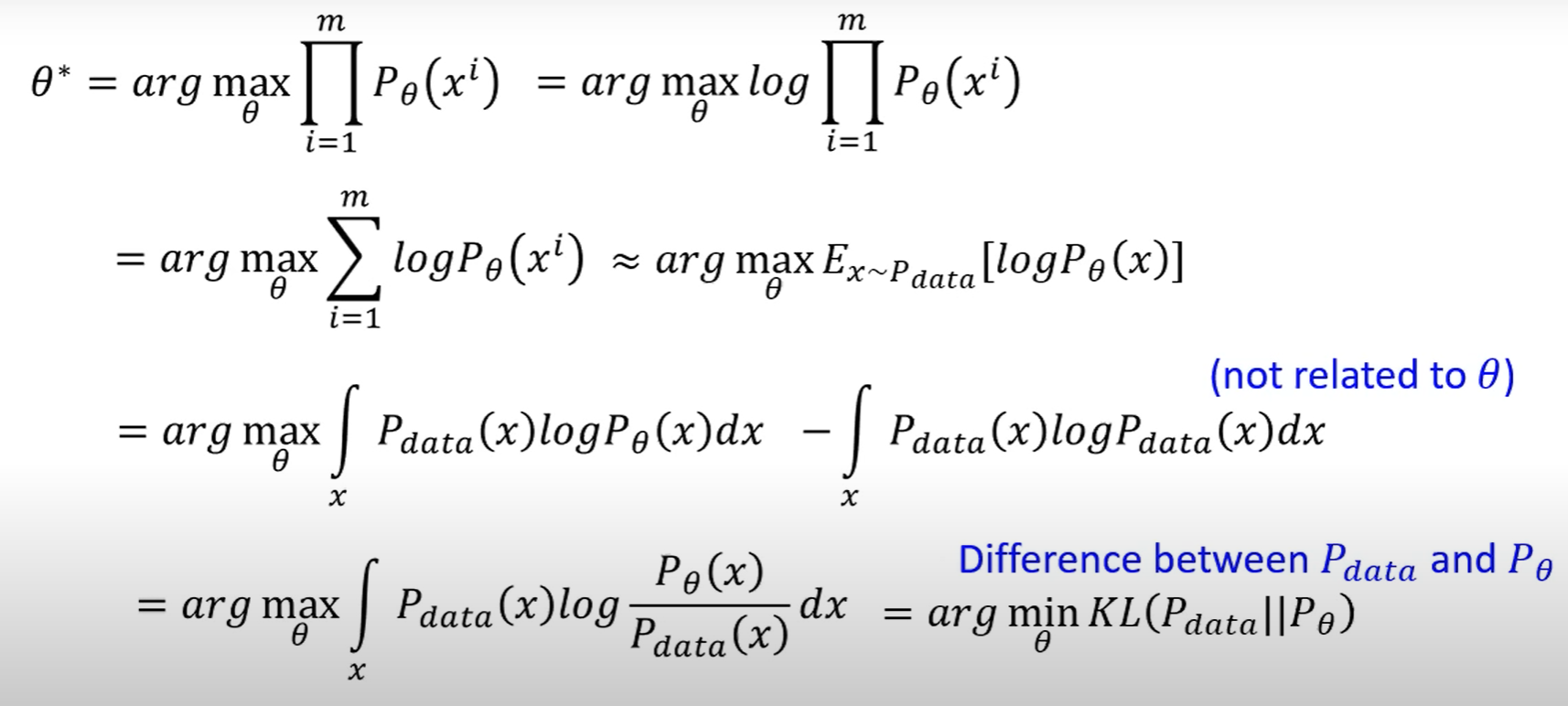
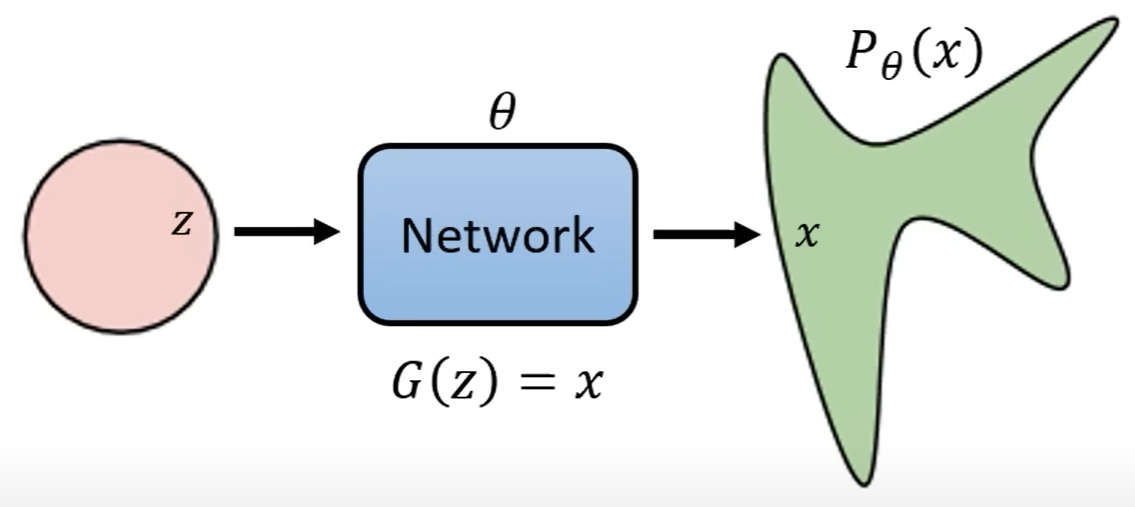
$P_\theta(x)=\int\limits_zP(z)P_\theta(x|z)dz$
$\begin{aligned}&P_\theta(x|\mathrm{z})\propto\exp(-|G(\mathrm{z})-x|_2)\end{aligned}$
Maximize : Lower bound of $logP(x)$
Flow-based Model
Diffusion Model
MLP
前向传播
根据每层的输入、权重weight和偏置bias,求出该层的输出,然后经过激活函数。按此一层一层传递,最终获得输出层的输出。
反向传播
神经网络之反向传播算法(BP)公式推导(超详细) - jsfantasy - 博客园 (cnblogs.com)
ML Lecture 7: Backpropagation - YouTube
假如激活函数为sigmoid函数:$\sigma(x) = \frac{1}{1+e^{-x}}$
sigmoid的导数为:$\frac{d}{dx}\sigma(x) = \frac{d}{dx} \left(\frac{1}{1+e^{-x}} \right)= \sigma(1-\sigma)$
因此当损失函数对权重求导,其结果与sigmoid的输出相关
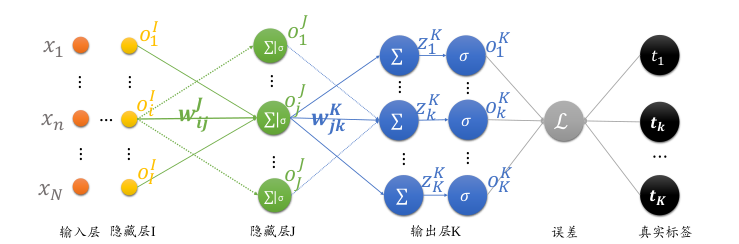
- o代表输出,上标表示当前的层数,下标表示当前层数的第几号输出
- z代表求和结果,即sigmoid的输入
- 权重$w^{J}_{ij}$的上标表示权值所属的层数,下标表示从I层的第i号节点到J层的第j号节点
输出对J层的权重$w_{ij}$求导:
$\frac{\partial z_k}{\partial w_{ij}} = \frac{\partial z_k}{o_j}\cdot \frac{\partial o_j}{\partial w_{ij}} = w_{jk} \cdot \frac{\partial o_j}{\partial w_{ij}}$, because $z_k = o_j \cdot w_{jk} + b_k$
and $\frac{\partial z_j}{\partial w_{ij}} = o_i \left(z_j = o_i\cdot w_{ij} + b_j\right)$
其中 $\delta_j^J = o_j(1-o_j) \cdot \sum_k \delta _k^K\cdot w_{jk}$
推广:
- 输出层:$\frac{\partial L}{\partial w_{jk}} = \delta _k^K\cdot o_j$ ,其中$\delta _k^K = (o_k-t_k)o_k(1-o_k)$
- 倒二层:$\frac{\partial L}{\partial w_{ij}} = \delta _j^J\cdot o_i$ ,其中$\delta_j^J = o_j(1-o_j) \cdot \sum_k \delta _k^K\cdot w_{jk}$
- 倒三层:$\frac{\partial L}{\partial w_{ni}} = \delta _i^I\cdot o_n$ ,其中$\delta_i^I = o_i(1-o_i)\cdot \sum_j\delta_j^J\cdot w_{ij}$
- $o_n$ 为倒三层输入,即倒四层的输出
根据每一层的输入或输出,以及真实值,即可计算loss对每个权重参数的导数
优化算法
不同的算法有不同的参数更新方式
优化的目标
训练数据集的最低经验风险可能与最低风险(泛化误差)不同
- 经验风险是训练数据集的平均损失
- 风险则是整个数据群的预期损失
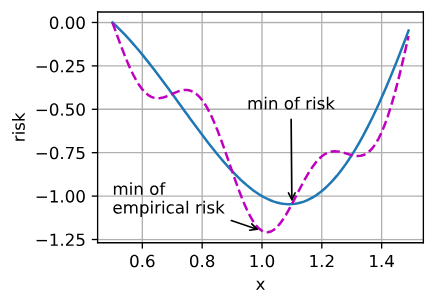
优化的挑战
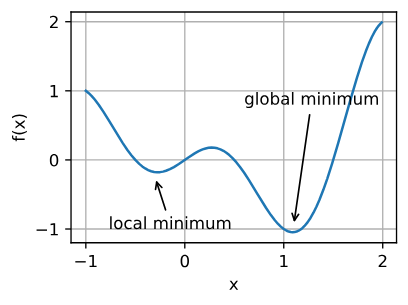
局部最优 |
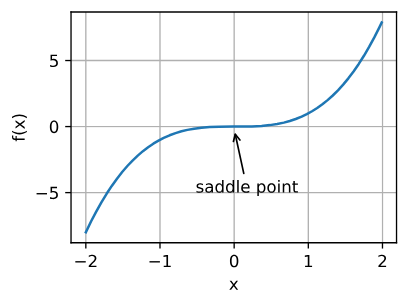
鞍点 |
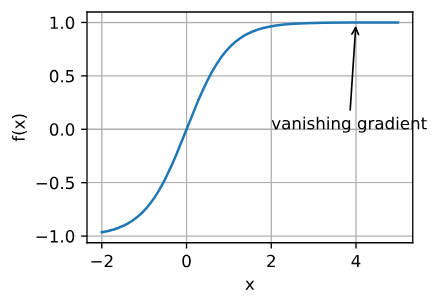
梯度消失 |
(鞍点 in 3D)saddle point be like: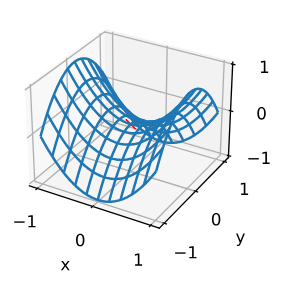
Transformer
The Illustrated Transformer – Jay Alammar – Visualizing machine learning one concept at a time.
The Transformer Family | Lil’Log
注意力机制的本质|Self-Attention|Transformer|QKV矩阵_哔哩哔哩_bilibili
输入X,通过三个不同的权重
$f(X)=softmax(XW_QX^TW_K/\sqrt{d})XW_V$ OR $\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}(\frac{\mathbf{Q} {\mathbf{K}}^\top}{\sqrt{d_k}})\mathbf{V}$
- $a_{ij} = \text{softmax}(\frac{\mathbf{q}_i {\mathbf{k}_j}^\top}{\sqrt{d_k}})= \frac{\exp(\mathbf{q}_i {\mathbf{k}_j}^\top)}{ \sqrt{d_k} \sum_{r \in S_i} \exp(\mathbf{q}_i {\mathbf{k}_r}^\top) }$
- 其中$\sqrt{d}$是为了防止维度过高导致的梯度消失,d是数据的维度
softmax(Q与K的乘积) 可以看作权重,通过权重来插值V得到最终的输出。通过使Q与K距离越小时,对
应的权重更大,即此时Key对应的Value对输出的贡献更大,让网络注意到这个贡献更大的Key
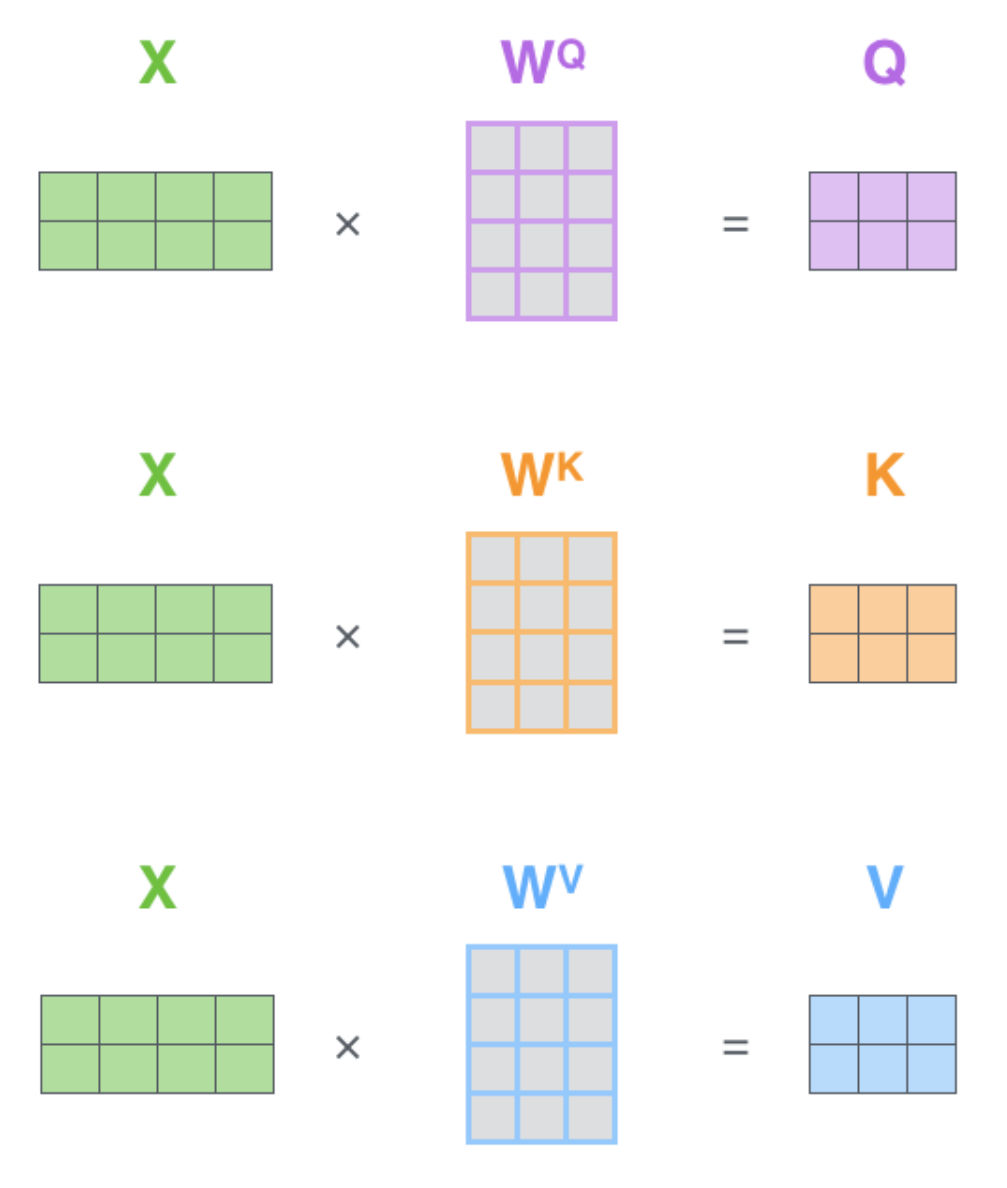
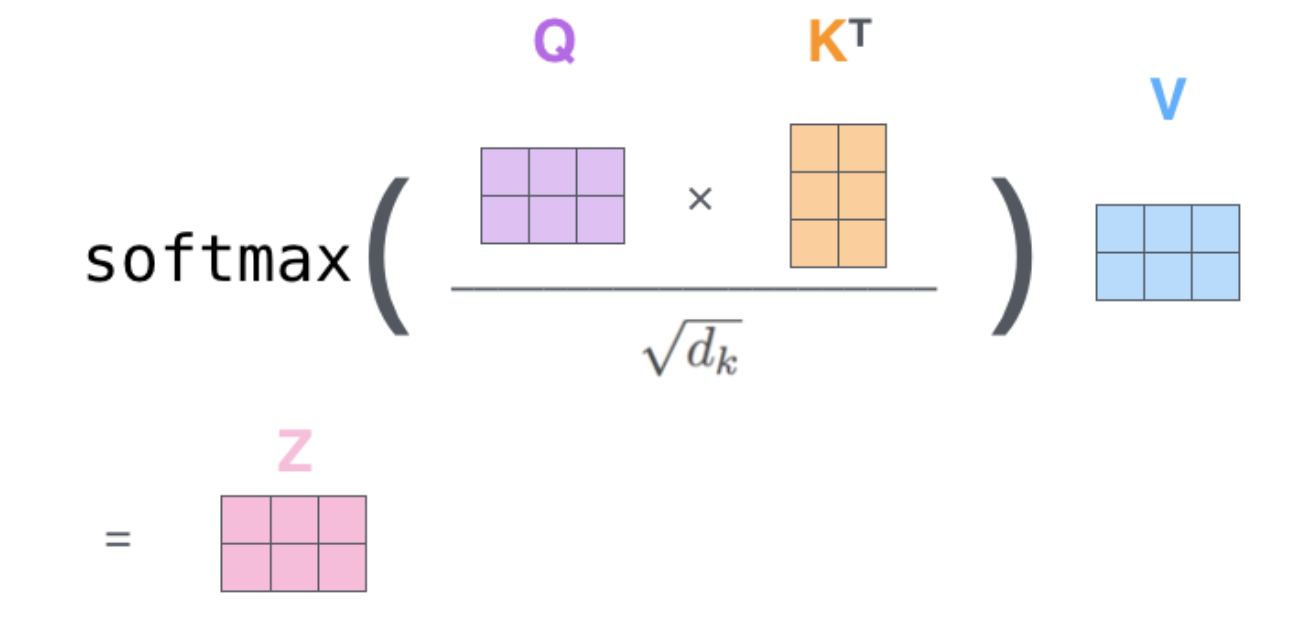
一个$\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}(\frac{\mathbf{Q} {\mathbf{K}}^\top}{\sqrt{d_k}})\mathbf{V}$计算为Attention的一个Head,多头注意力就是多个Head:
- $\begin{aligned}\text{MultiHeadAttention}(\mathbf{X}_q, \mathbf{X}_k, \mathbf{X}_v) &= [\text{head}_1; \dots; \text{head}_h] \mathbf{W}^o \\ \text{where head}_i &= \text{Attention}(\mathbf{X}_q\mathbf{W}^q_i, \mathbf{X}_k\mathbf{W}^k_i, \mathbf{X}_v\mathbf{W}^v_i)\end{aligned}$
- $\mathbf{W}^o \in \mathbb{R}^{d_v \times d}$ 为输出的线性transformation
vanilla Transformer model: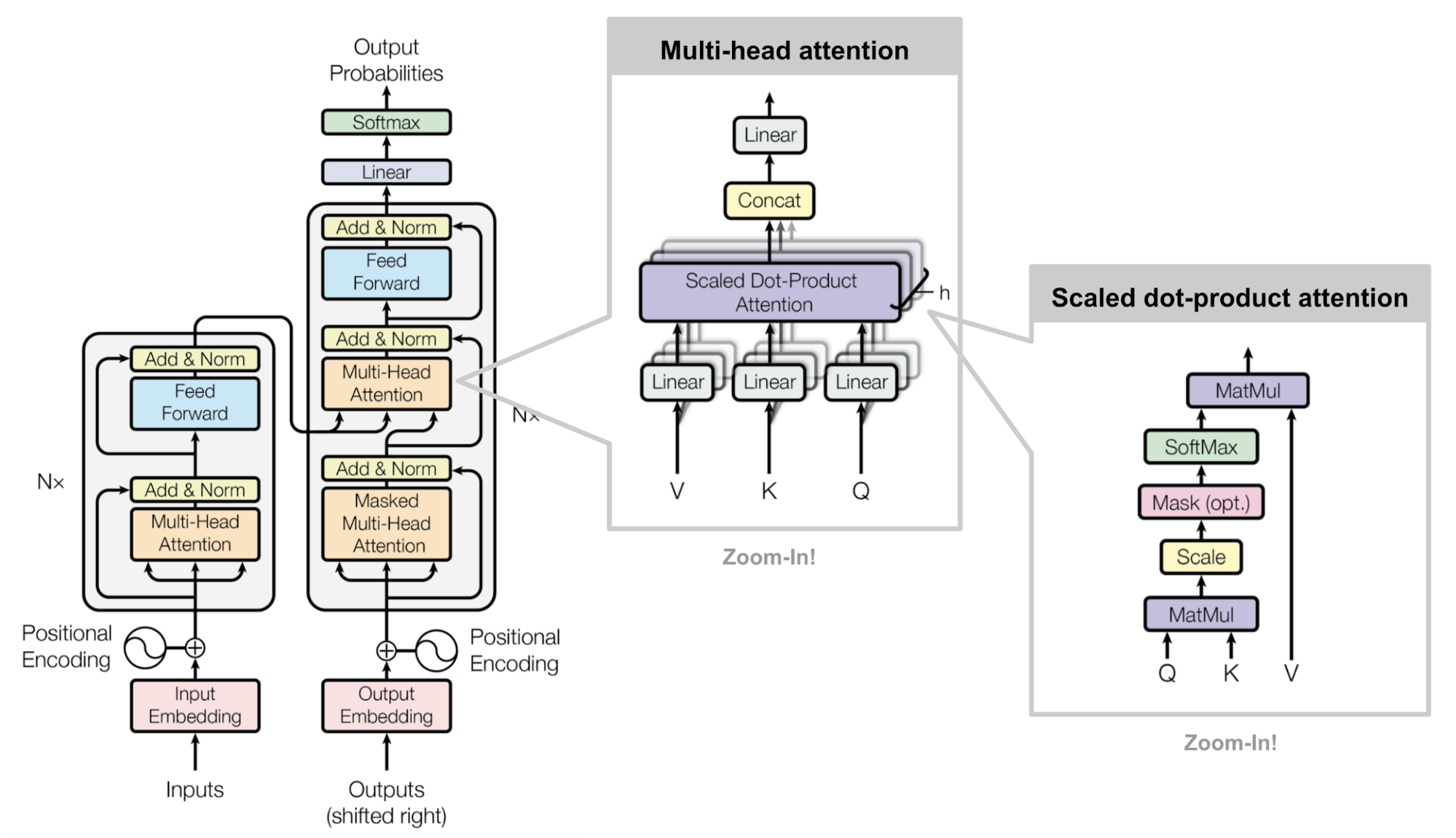
Positiolal Encoding
- the token position $i=1,\dots,L$
- the dimension $\delta=1,\dots,d$
_Learned positional encoding_, as its name suggested, assigns each element with a learned column vector which encodes its _absolute_ position
Convolutional Sequence to Sequence Learning | Abstract
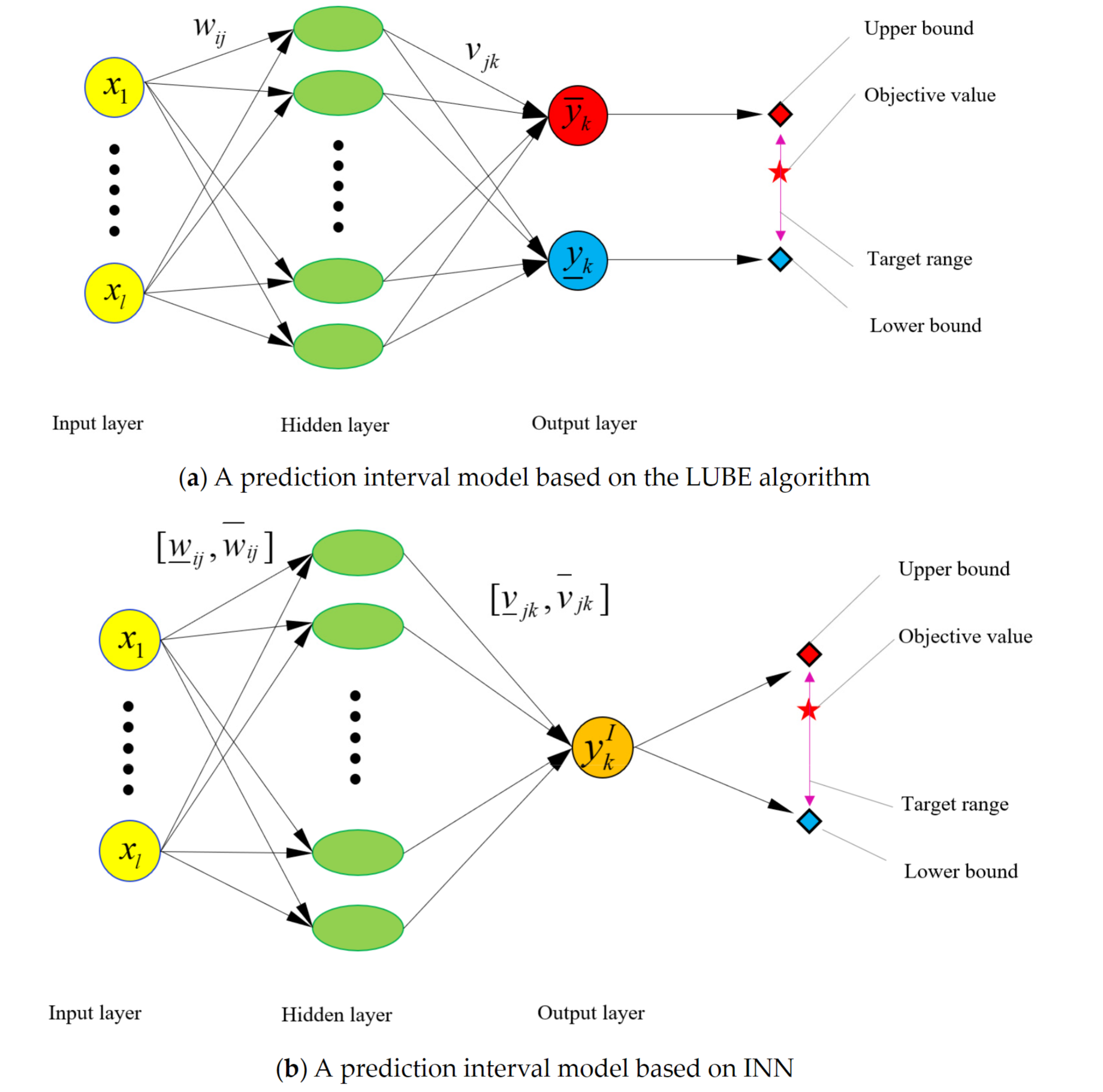
INN
Interval Neural Networks 2020 通过物理参数和measured response来辨识 集中负载
$y_{k}^{I}=f(x_{1},x_{2},\cdots,x_{l})=[\underline{y}_{k},\overline{y}_{k}]=f\left(\sum_{j=1}^{m}\left[\underline{v}_{jk},\overline{v}_{jk}\right]u_{j}-[\underline{\lambda}_{k},\overline{\lambda}_{k}]\right)$
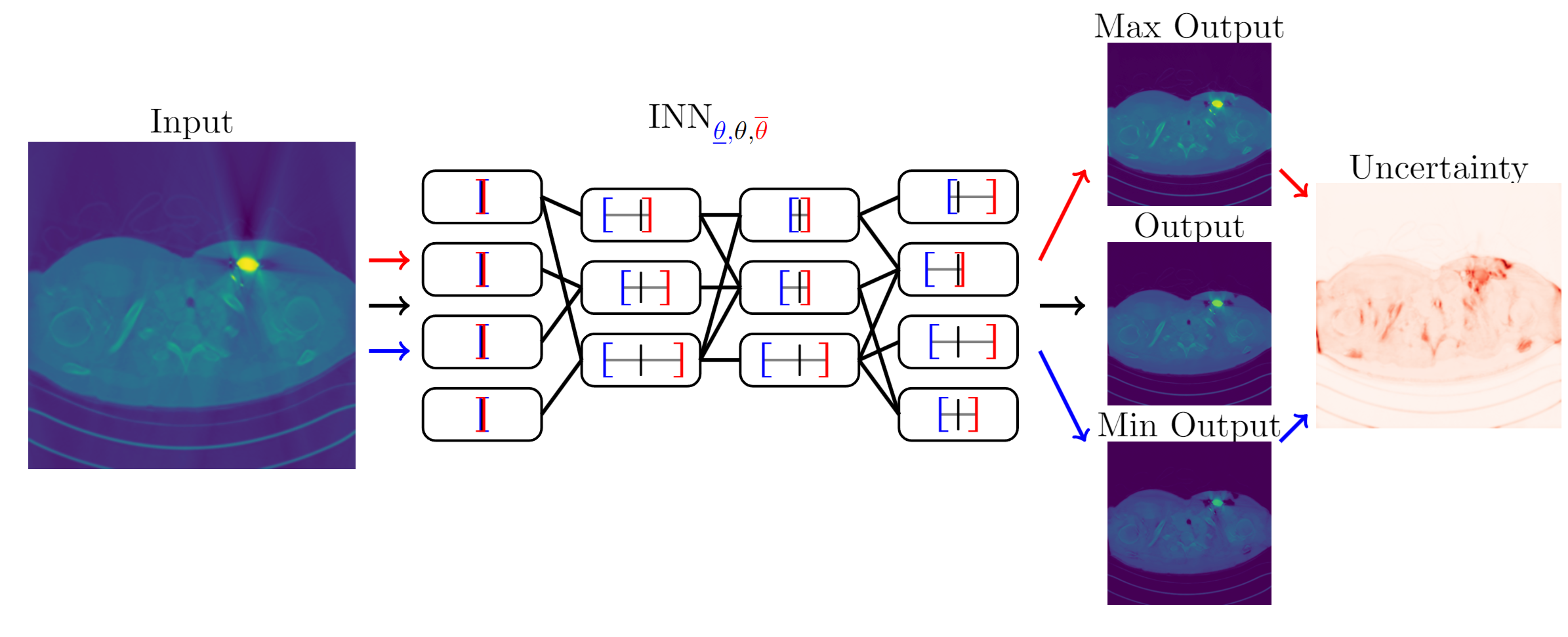
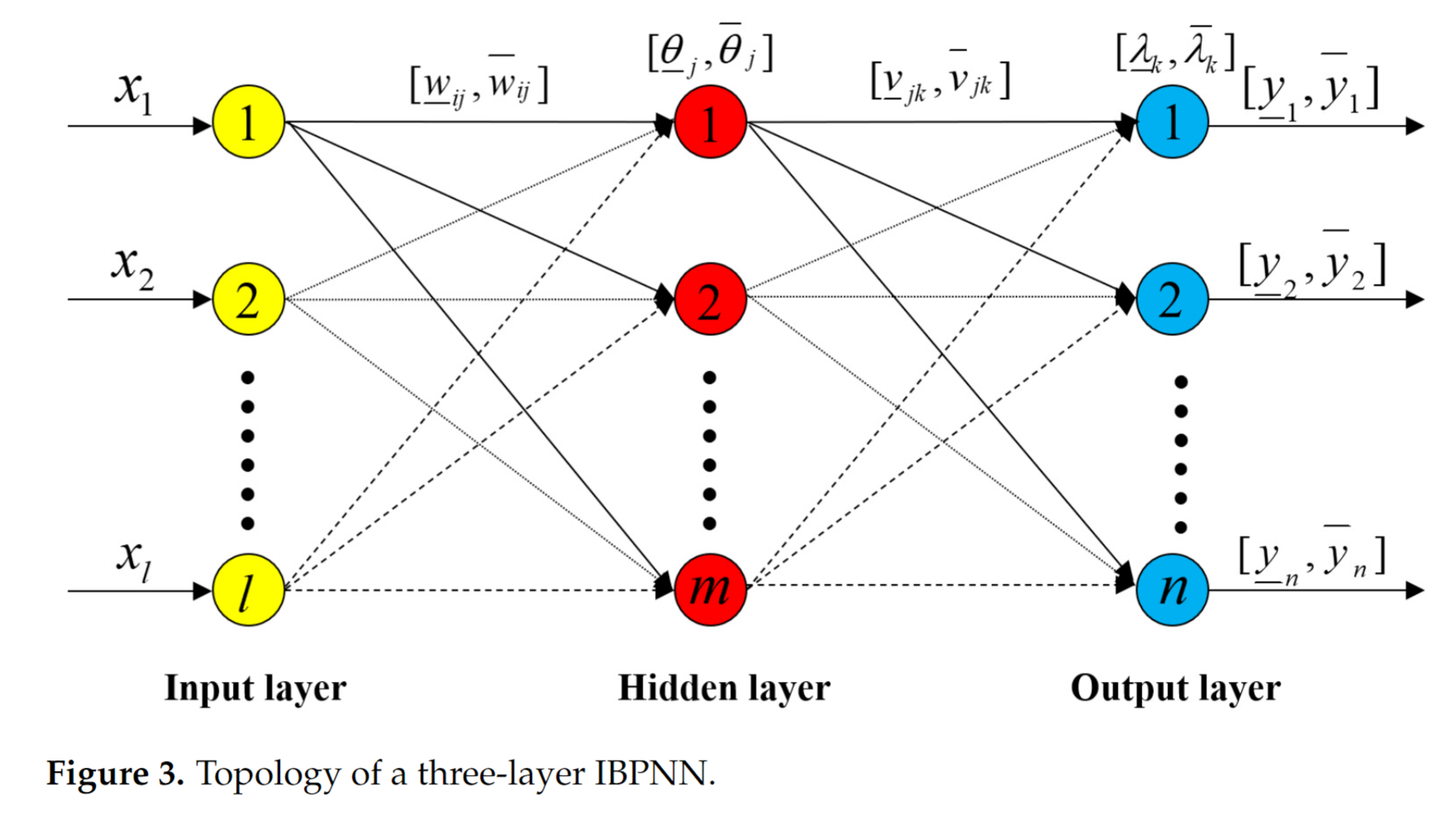
INN 与 MLP 两者预测区间参数的区别
INN offers greater fitting flexibility due to the interval of weight and bias
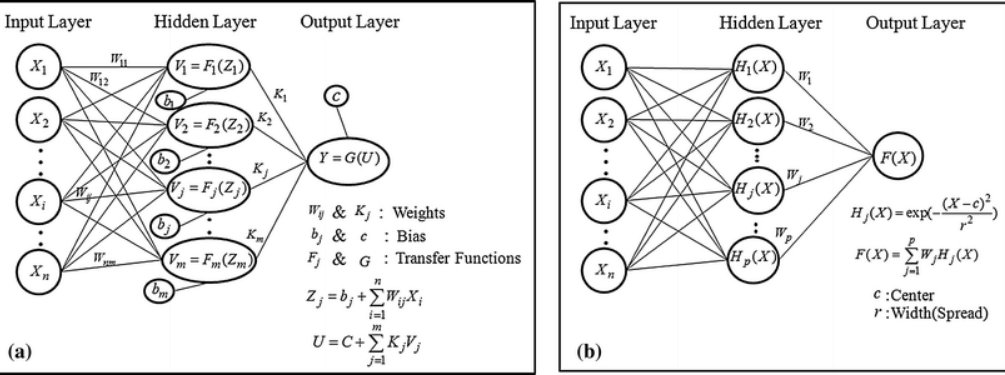
RBFNN
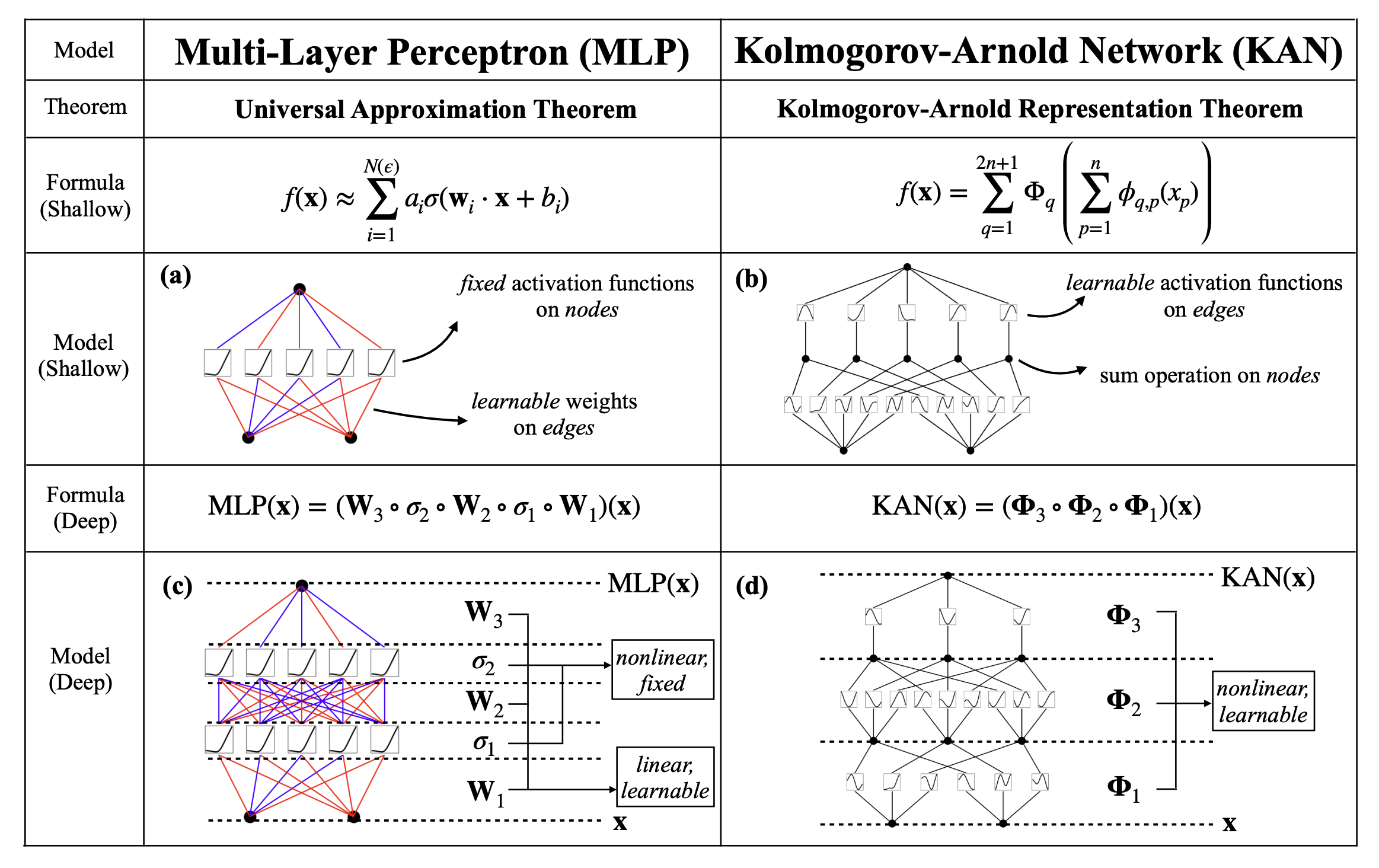
KAN
KindXiaoming/pykan: Kolmogorov Arnold Networks
SNNs
第三代神经网络初探:脉冲神经网络(Spiking Neural Networks) - 知乎
Kriging(Physical-law embedded)
GNN
A Gentle Introduction to Graph Neural Networks
(21 封私信 / 3 条消息) 图神经网络(GNN)最简单全面原理与代码实现! - 知乎
其他概念
参数重整化
DDPMb站视频公式推导
从高斯分布中直接采样一个值出来是不可导的,无法进行梯度传递,需要进行参数重整化:
从 $\mathcal{N}(0,1)$ 中随机采样出来 z,然后对 z 做 $\mu + z * \sigma$ 相当于从高斯分布 $\mathcal{N}(\mu,\sigma)$ 中采样
位置编码
Position Embedding 与 Position encoding的区别
position embedding:随网络一起训练出来的位置向量,与前面说的一致,可以理解成动态的,即每次训练结果可能不一样。
position encoding:根据一定的编码规则计算出来位置表示,比如
迁移学习
迁移学习通常会关注有一个源域 $D_{s}$ 和一个目标域$D_{t}$ 的情况,将源域中网络学习到的知识迁移到目标域的学习中
Transfer learning 【迁移学习综述_汇总】 - 知乎 (zhihu.com)
集成学习
集成学习(Ensemble Learning) - 知乎 (zhihu.com)
