Diffusion Model

2. 扩散概率模型（diffusion probabilistic models） — 张振虎的博客张振虎文档

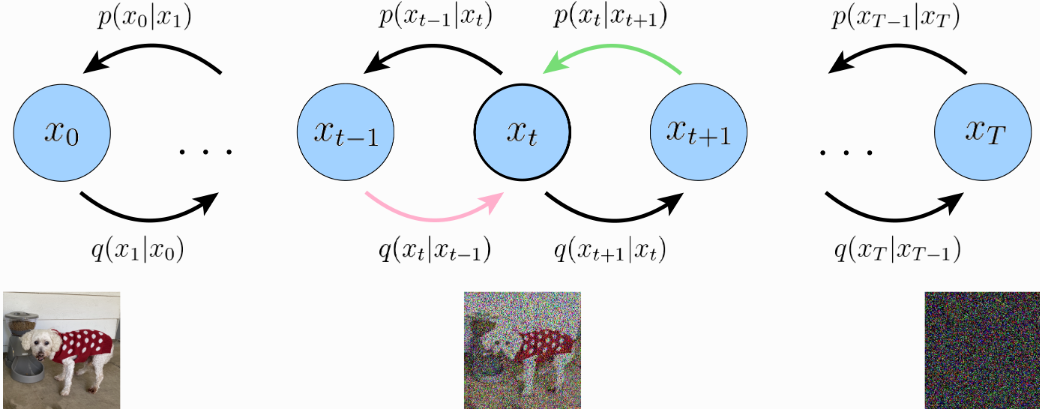
$q(x_t|x_{t-1}) = \mathcal{N} (\sqrt{\alpha_t} \ x_{t-1}, (1- \alpha_t ) \textit{I} )$

$\begin{align}\begin{aligned}x_{t} &=\sqrt{\alpha_t} \ x_{t-1} + \mathcal{N} (0, (1- \alpha_t ) \textit{I} )\\&=\sqrt{\alpha_t} \ x_{t-1} + \sqrt{1- \alpha_t } \ \epsilon \ \ \ ,\epsilon \sim \mathcal{N} (0, \textit{I} )\end{aligned}\end{align}$

随着t的增大，$\alpha_{t}$在逐渐变小。这是由于前期如果加的噪声太多，会使得数据扩展的太快（比如突变），使得逆向还原变得困难；同样因为后期数据本身已经接近随机噪声数据了，后期如果加的噪声不够多，相当于变化幅度小，扩散的太慢，这会使得链路变长需要的事件变多。我们希望扩散的前期慢一点，后期快一点

通过设定超参数$\alpha_{0:T}$可以看出前向加噪的过程是可以直接通过公式计算的，没有未知参数。

$\begin{align}\begin{aligned}x_t &= \sqrt{\alpha_t} \ x_{t-1} + \sqrt{1-\alpha_t} \ \epsilon_{t}\\&= \sqrt{\alpha_t} \left( \sqrt{\alpha_{t-1}} \ x_{t-2} + \sqrt{1-\alpha_{t-1}} \ \epsilon_{t-1} \right ) + \sqrt{1-\alpha_t} \ \epsilon_{t}\\&= \sqrt{\alpha_t \alpha_{t-1} } \ x_{t-2} + \underbrace{ \sqrt{\alpha_t - \alpha_t \alpha_{t-1} }\ \epsilon_{t-1} + \sqrt{1- \alpha_t} \ \epsilon_{t} }_{\text{两个相互独立的0均值的高斯分布相加}}\\ &= \sqrt{\alpha_t \alpha_{t-1} } \ x_{t-2} + \underbrace{ \sqrt{ \sqrt{\alpha_t - \alpha_t \alpha_{t-1} }^2 + \sqrt{1- \alpha_t}^2 } \ \epsilon }_{\text{两个方差相加，用一个新的高斯分布代替}}\\&= \sqrt{\alpha_t \alpha_{t-1} } \ x_{t-2} + \sqrt{1- \alpha_t \alpha_{t-1}} \ \epsilon\\&= ...\\&= \sqrt{\prod_{i=1}^t \alpha_i} \ x_0 + \sqrt{1- \prod_{i=1}^t \alpha_i } \ \epsilon\\&= \sqrt{\bar{ \alpha}_t } \ x_0 + \sqrt{1- \bar{ \alpha}_t } \ \epsilon \ \ \ , \bar{\alpha} = \prod_{i=1}^t \alpha_i ,\ \ \epsilon \sim \mathcal{N}(0,\textit{I})\\&\sim \mathcal{N}(\sqrt{\bar{\alpha}_t } \ x_0, (1- \bar{ \alpha}_t) \textit{I})\end{aligned}\end{align}$

而逆向过程需要从噪声开始，逐步解码成一个有意义的数据 $p(x_{0:T}) = p(x_T) \prod_{t={T-1}}^0 p(x_{t}|x_{t+1})$

在这里$p(x_T) \sim \mathcal{N}(0,\textit{I})$ 是高斯分布，但是$p_{\theta}(x_{t}|x_{t+1})$ 是难以求解的(分母部分含有积分，且没有解析解)，依次使用网络来拟合学习这一条件概率分布 $p(x_{t}|x_{t+1})=\frac{p(x_{t},x_{t+1})}{p(x_{t+1})}=\frac{p(x_{t+1}|x_{t})p(x_{t})}{\int_{-\infty}^{+\infty}p(x_{t+1}|x_{t})p(x_{t})dx_{t}}.$
目标函数（ELBO）我们知道学习一个概率分布的未知参数的常用算法是极大似然估计，极大似然估计是通过极大化观测数据的对数概率（似然）实现的

DDPM(Denoising Diffusion Probabilistic Models)

$\text{Maximize E}_{q(x_1:x_T|x_0)}[log\left(\frac{P(x_0;x_T)}{q(x_1:x_T|x_0)}\right)]$

$q(x_t|x_0)$ 可以只做一次 sample(给定一系列 $\beta$)

DDPM 的 Lower bound of $logP(x)$
复杂公式推导得到： ELBO函数来约束网络训练
$logP(x) \geq \operatorname{E}_{q(x_1|x_0)}[logP(x_0|x_1)]-KL\big(q(x_T|x_0)||P(x_T)\big)-\sum_{t=2}^{T}\mathrm{E}_{q(x_{t}|x_{0})}\bigl[KL\bigl(q(x_{t-1}|x_{t},x_{0})||P(x_{t-1}|x_{t})\bigr)\bigr]$

$\mathbb{E}_{q(x_{1}|x_0)}\left[\ln p_{\theta}(x_0|x_1)\right]$ 重建项，从隐式变量中重建出原来的数据$x_{0}$
$\mathbb{E}_{q(x_{T-1}|x_0)}\left[D_{KL}{q(x_T|x_{T-1})}{p(x_T)}\right]$ 最后一个数据是高斯噪声，因此当T足够大，这一项趋于0
$\mathbb{E}_{q(x_{t-1}, x_{t+1}|x_0)}\left[D_{KL}{q(x_{t}|x_{t-1})}{p_(x_{t}|x_{t+1})}\right]$ KL散度度量， consistency term。这一项用来最小化$q(x_{t}|x_{t-1})$ 与 $p_(x_{t}|x_{t+1})$ 之间的差异。期望是关于两个变量的，用采样法（MCMC）同时对两个随机变量进行采样，会导致更大的方差，这会使得优化过程不稳定，不容易收敛，可以将$p_(x_{t}|x_{t+1})$优化为：$q(x_{t-1}|x_t, x_0)$

$q(x_t | x_{t-1}, x_0) = \frac{q(x_{t-1} \mid x_t, x_0)q(x_t \mid x_0)}{q(x_{t-1} \mid x_0)}$

条件独立性：假设有三个随机变量A，B，C，三者依赖关系：A—>B—>C，当B值已知时，A和C相互独立，此时$P(C|B)=P(C|B,A)$ 成立 $q(x_t | x_{t-1}) = q(x_t | x_{t-1}, x_0)$
联合概率的基本性质：$q(x_t, x_{t-1}, x_0) = q(x_t \mid x_{t-1}, x_0) q(x_{t-1} \mid x_0) q(x_0)$ 另一种形式$q(x_t, x_{t-1}, x_0) = q(x_{t-1} \mid x_t, x_0) q(x_t \mid x_0) q(x_0)$

$q(x_t \mid x_{t-1}, x_0) q(x_{t-1} \mid x_0) q(x_0) = q(x_{t-1} \mid x_t, x_0) q(x_t \mid x_0) q(x_0)$
即得$q(x_t | x_{t-1}, x_0) = \frac{q(x_{t-1} \mid x_t, x_0)q(x_t \mid x_0)}{q(x_{t-1} \mid x_0)}$ 和 $q(x_{t-1}|x_{t},x_{0}) =\frac{q(x_{t}|x_{t-1})q(x_{t-1}|x_{0})}{q(x_{t}|x_{0})}$

直接预测原始样本 $x_t=\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon.$

$q(x_{t-1}|x_{t},x_{0}) =\frac{q(x_{t}|x_{t-1})q(x_{t-1}|x_{0})}{q(x_{t}|x_{0})}$ 为一个 Gaussian distribution 推导过程
- 均值+方差： $mean = \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_{t}x_{0}+\sqrt{\alpha_{t}}(1-\bar{\alpha}_{t-1})x_{t}}{1-\bar{\alpha}_{t}}$ ，$variance = \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta$

$x_0$需要通过网络预测来获得，因此：
$\mu_q(x_t, x_0) = { \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_{t} + \sqrt{\bar\alpha_{t-1}}(1-\alpha_t)x_0}{1 -\bar\alpha_{t}}}$
$\mu_{\theta}={\mu}_(x_t, t) = \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_{t} + \sqrt{\bar\alpha_{t-1}}(1-\alpha_t)\hat x_(x_t, t)}{1 -\bar\alpha_{t}}$ 网络预测$\hat{x}_{\theta}$ ，然后这个分布，采样得到$x_{t-1}$

然而直接预测$x_{0}$时非常困难得，每个步骤都只给定每一步的t来预测同样的输出，(trained)相同的网络参数很难完成这样的预测

因此DDPM转换思路来预测每步t中添加的噪声：
$x_0 = \frac{x_t -\sqrt{1- \bar{ \alpha}_t } \ \epsilon_t }{ \sqrt{\bar{\alpha}_t } },\ \ \epsilon_t \sim \mathcal{N}(0,\textit{I})$

均值：$\mu_{\theta}={\mu}_(x_t, t) = \frac{1}{\sqrt{\alpha_t}}x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar\alpha_t}\sqrt{\alpha_t}} {\hat\epsilon}_{ {\theta}}(x_t, t)$ 推导过程 (将$x_{0}$重写成$\epsilon$)

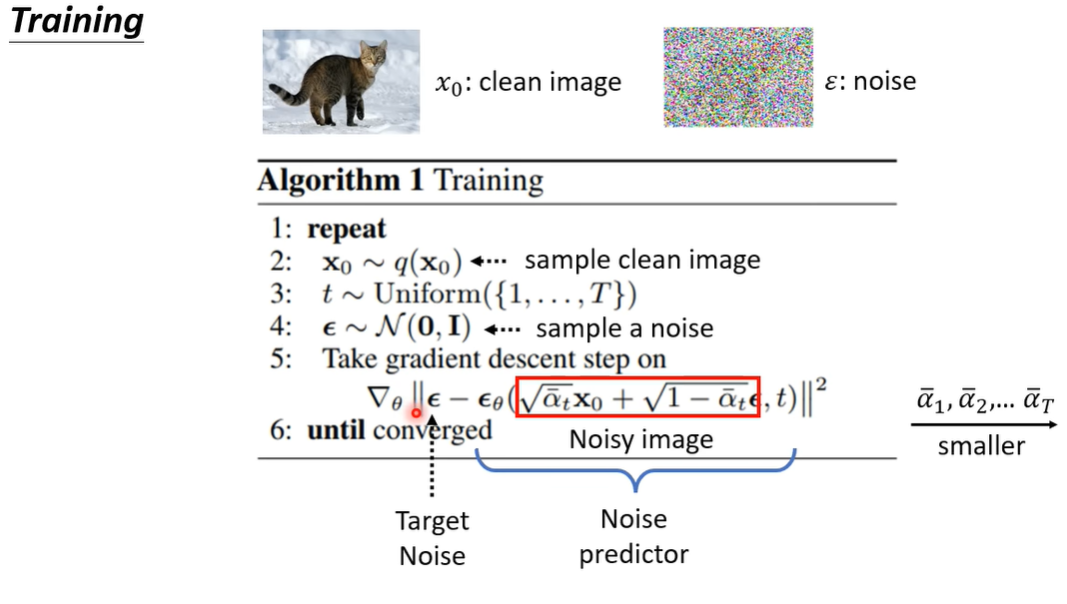
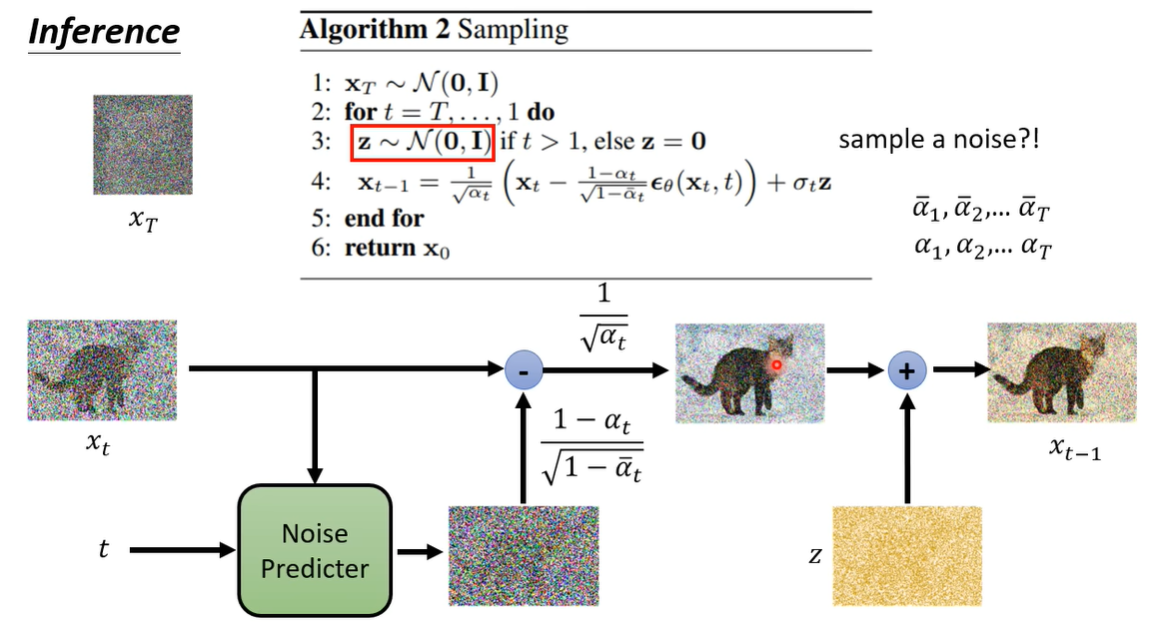
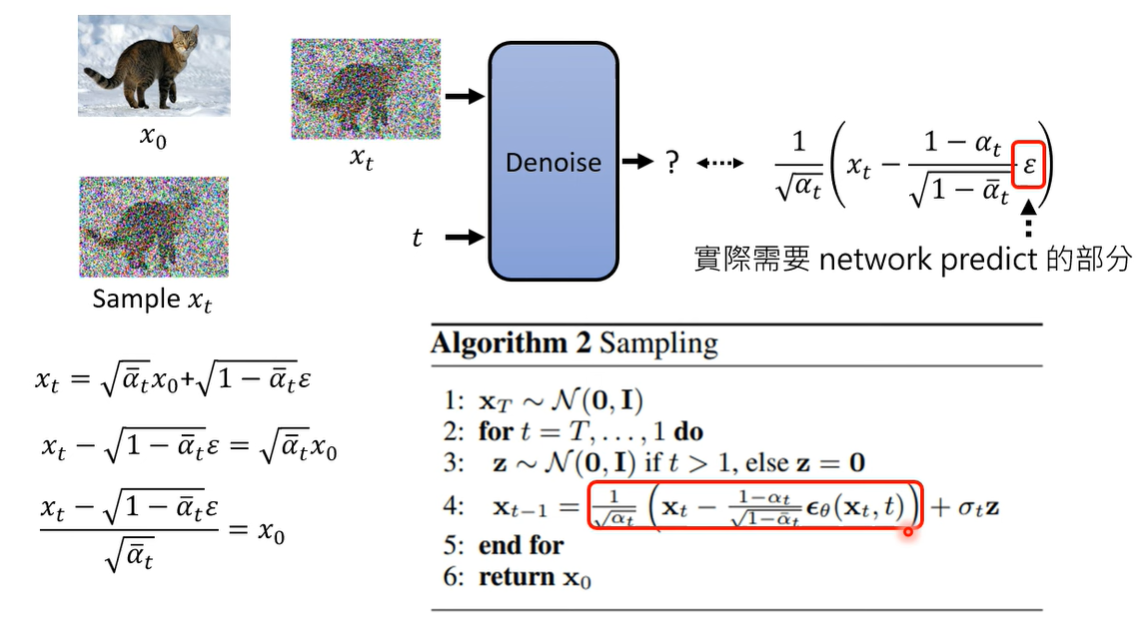
DDPM 三种形式

逆向生成过程：$q(x_{t-1}|x_t,x_0) \sim \mathcal{N}(x_{t-1},\mu_q,\Sigma_{q(t)})$

方差：
$\Sigma_q(t) = \frac{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}{ 1 -\bar\alpha_{t}} \textit{I} = \sigma_q^2(t) \textit{I}$

1）直接预测初始样本

$\mu_q(x_t, x_0) = { \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_{t} + \sqrt{\bar\alpha_{t-1}}(1-\alpha_t)x_0}{1 -\bar\alpha_{t}}}$

$\mu_{\theta}={\mu}_(x_t, t) = \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_{t} + \sqrt{\bar\alpha_{t-1}}(1-\alpha_t)\hat x_(x_t, t)}{1 -\bar\alpha_{t}}$

2）预测噪声

$\mu_q(x_t, x_0) = \frac{1}{\sqrt{\alpha_t}}x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar\alpha_t}\sqrt{\alpha_t}}\ \epsilon$

$\mu_{\theta}={\mu}_(x_t, t) = \frac{1}{\sqrt{\alpha_t}}x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar\alpha_t}\sqrt{\alpha_t}} {\hat\epsilon}_{ {\theta}}(x_t, t)$

3）预测分数

${\mu}_q(x_t, x_0) = \frac{1}{\sqrt{\alpha_t}}x_t + \frac{1 - \alpha_t}{\sqrt{\alpha_t}}\nabla\log p(x_t)$

${\mu}_q(x_t, x_0) = \frac{1}{\sqrt{\alpha_t}}x_t + \frac{1 - \alpha_t}{\sqrt{\alpha_t}} s_{\theta}(x_t,t)$

DDPM Code

mikonvergence/DiffusionFastForward: DiffusionFastForward: a free course and experimental framework for diffusion-based generative models (github.com)

Schedule

betas: $\beta_t$ , betas=torch.linspace(1e-4,2e-2,num_timesteps)
alphas: $\alpha_t=1-\beta_t$
alphas_sqrt: $\sqrt{\alpha_t}$
alphas_prod: $\bar{\alpha}_t=\prod_{i=0}^{t}\alpha_i$
alphas_prod_sqrt: $\sqrt{\bar{\alpha}_t}$

diffusion step 0,1,…,t,…T：随着t增大，beta应该逐渐增大

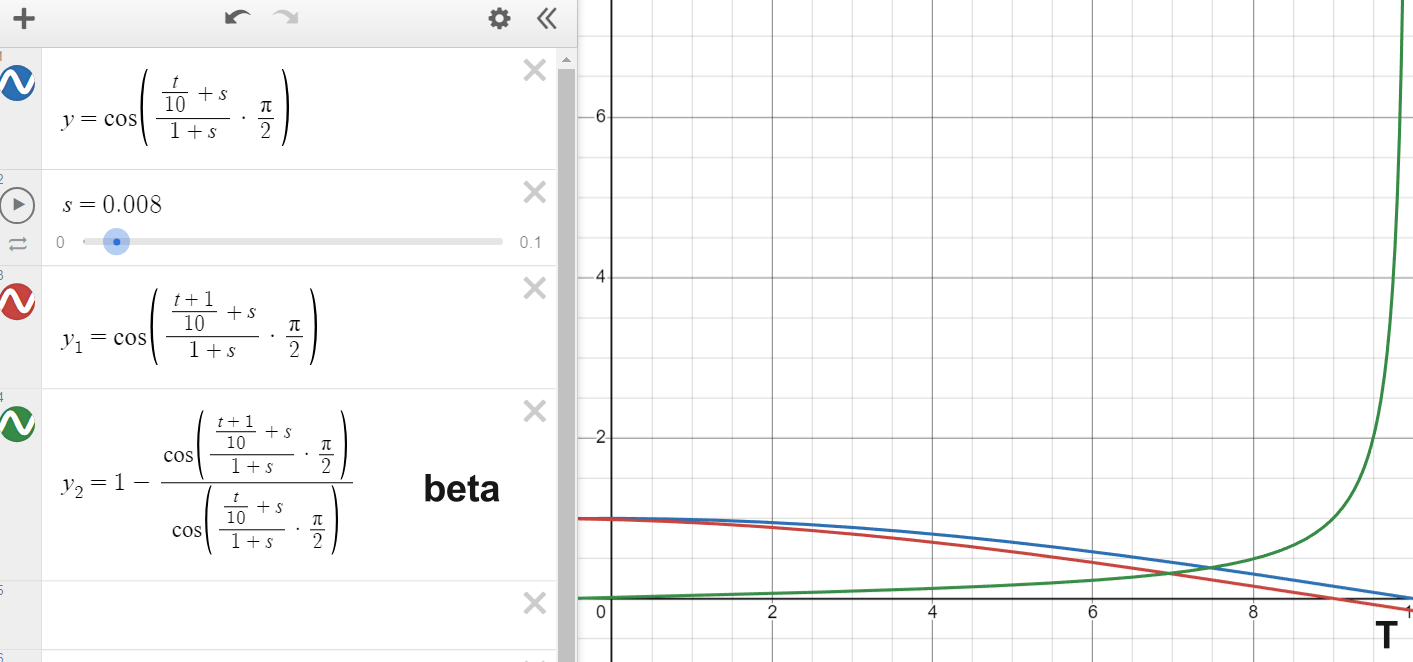
cosine:
- $\alpha_{cumprod} =\cos\left( \left( \frac{\frac{t}{T}+s}{(1+s)}\cdot \pi \cdot 0.5 \right)^{2} \right)$ ，value: $\cos\left( \frac{s}{1+s} \cdot \frac{\pi}{2} \right)$ ~$\cos\left( \frac{\pi}{2} \right)$ = $\cos(0)$ ~ $\cos\left( \frac{\pi}{2} \right)$ if s —> 0
- $\alpha_{cumprod} = \frac{\alpha_{cumprod}}{\alpha_{cumprod}^{max}}$, 让最大的$\alpha$不超过1
- $\beta$ = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
linear:
- $linspace\left( scale0.0001,scale0.02,T \right)$ , $scale=\frac{1000}{T}$

# consine beta
def cosine_beta_schedule(timesteps, s=0.008):
  """
  cosine schedule
  as proposed in https://openreview.net/forum?id=-NEXDKk8gZ
  """
  steps = timesteps + 1
  x = torch.linspace(0, timesteps, steps, dtype=torch.float64)
  alphas_cumprod = torch.cos(((x / timesteps) + s) / (1 + s) * math.pi * 0.5) ** 2
  alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
  betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
  return torch.clip(betas, 0, 0.999)

# linear beta
def linear_beta_schedule(timesteps):
  scale = 1000 / timesteps
  beta_start = scale * 0.0001
  beta_end = scale * 0.02
  return torch.linspace(beta_start, beta_end, timesteps, dtype=torch.float64)

Forward Process

Forward step:

$q(x_t|x_{t−1}) := \mathcal{N}(x_t; \sqrt{1 − \beta_t}x_{t−1}, \beta_tI) \tag{1}$

Forward jump:

$q(x_t|x_0) = \mathcal{N}(x_t;\sqrt{\bar{\alpha_t}}x_0, (1 − \bar{\alpha_t})I) \tag{2}$

def forward_step(t, condition_img, return_noise=False):
    """
        forward step: t-1 -> t
    """
    assert t >= 0

    mean=alphas_sqrt[t]*condition_img
    std=betas[t].sqrt()

    # sampling from N
    if not return_noise:
        return mean+std*torch.randn_like(img)
    else:
        noise=torch.randn_like(img)
        return mean+std*noise, noise

def forward_jump(t, condition_img, condition_idx=0, return_noise=False):
    """
        forward jump: 0 -> t
    """
    assert t >= 0

    mean=alphas_cumprod_sqrt[t]*condition_img
    std=(1-alphas_cumprod[t]).sqrt()

    # sampling from N
    if not return_noise:
        return mean+std*torch.randn_like(img)
    else:
        noise=torch.randn_like(img)
        return mean+std*noise, noise

Reverse Process

至少三种逆向过程的求法，从 $x_{t}$ 到 $x_{0}$
There are at least 3 ways of parameterizing the mean of the reverse step distribution $p_\theta(x_{t-1}|x_t)$:

Directly (a neural network will estimate $\mu_\theta$)直接用网络预测 $\mu_\theta$
Via $x_0$ (a neural network will estimate $x_0$)用网络预测 $x_0$ $\tilde{\mu}_\theta = \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t\tag{4}$
Via noise $\epsilon$ subtraction from $x_0$ (a neural network will estimate $\epsilon$)用网络预测噪声 $\epsilon$ $x_0=\frac{1}{\sqrt{\bar{\alpha}_t}}(x_t-\sqrt{1-\bar{\alpha}_t}\epsilon)\tag{5}$

Why Does Diffusion Work Better than Auto-Regression?

Why Does Diffusion Work Better than Auto-Regression? - YouTube

分类任务：图片—>类别

如何生成图片(Thinking)：

从任意数据中预测整张图片(真实图片做标签)，这样训练集标签图片的mean value会变blurring(blurry mess)。(分类任务中训练集标签01的meaning value不会收到很大影响)
Auto-Regressor: 正向过程是不断擦除图像，网络被训练为undo这个过程，即不断预测图片的下一个像素是什么颜色(like ChatGPT)
- 考虑来预测图片中的单个像素，这样训练集标签的mean value是另一个颜色值(网络根据输入的图片来预测单个颜色值)。每个像素的颜色训练一个网络来进行预测，通过多个网络，依次预测每个像素值，最终得到整张图片。这样就能生成plausible(似乎是真的) image，out of nothing(凭空)。然而每次生成的图片是相同的
- 考虑添加随机，之前predicted pixel是概率分布中概率最大的那个颜色值，不去这样选择而是随机选择某个概率的颜色作为本次的预测
- 缺点是随着像素量的增大，计算量非常大，要生成一张大像素图像是非常耗时的。当然可以造数据集时一次remove多个像素，在训练中一次预测多个像素。但是不能过多，这样依然会造成blurry mess Trade-off：更快但是blurry mess，更慢但是更准确

Blurry mess：

Why predicting one pixel is work：

该问题只会出现在预测的值是互相关的情况(在图像中相近的像素通常是强相关的，这在按顺序remove时出现)，假设预测的值相互独立的情况(随机remove像素)。remove像素可以从另一种角度进行实现，即给每个像素添加噪声

Stable Diffusion

Stable Diffusion 图片生成原理简述 « bang’s blog

目前常见的 UI 有 WebUI 和 ComfyUI

模型

模型格式：

主模型 checkpoints：ckpt, safetensors
微调模型
- LoRA 和 LyCORIS 控制画风和角色：safetensors
- 文本编码器模型：pt,safetensors
  - Embedding 输入文本 prompt 进行编码 pt
- Hypernetworks 低配版的 lora pt
- ControlNet
- VAE 图片与潜在空间 pt

采样器

Stable diffusion采样器全解析，30种采样算法教程
DPM++2M Karras，收敛+速度快+质量 OK