QiYun

Note

Kriging

Posted on Edited on In
4.8k 17 mins.

Kriging Model

Kriging

(11 封私信) 克里金(Kriging)模型详细推导 - 知乎
(11 封私信) 高斯过程 Gaussian Processes 原理、可视化及代码实现 - 知乎

文献形式：
$\left.\left\{\begin{array}{l}\hat{y}_1(x)=\hat{\mu}+r^TC^{-1}(y-\mathbf{1}\hat{\mu})\\s_1^2(x)=\hat{\sigma}^2[1-r^TC^{-1}r+\frac{(1-\mathbf{1}^TC^{-1}r)^2}{\mathbf{1}^TC^{-1}\mathbf{1}}]\end{array}\right.\right.$
$\left\{\begin{array}{l}\hat{\mu}=\frac{\mathbf{1}^TC^{-1}y}{\mathbf{1}^TC^{-1}\mathbf{1}}\\\hat{\sigma}^2=\frac{(y-\mathbf{1}\hat{\mu})^TC^{-1}(y-\mathbf{1}\hat{\mu})}{n}\end{array}\right.$

  • 其中$\hat{y}(x)$为预测点x的均值，$s^{2}(x)$为预测点x的方差，$r$是数据点X和预测点x之间的协方差矩阵，C是数据点X的协方差矩阵，$y$是数据点的目标值。$\mathbf{1}$是$n \times 1$的矩阵

DACE(matlab)程序形式：当基函数是0次函数，f(x)=1时，$F=\mathbf{1}$是$n \times 1$的矩阵，f=1为标量，此时可以推导出文献形式的公式

  • 其中$f(x)$是回归的模型，可选0/1/2次多项式。$r(x)$是相关函数(高斯核函数/指数核函数)

Train/Fit

对于给定数据集$\{\mathbf{X},\mathbf{y}\}_{i=1}^{n}$，Kriging假设数据都服从n维正态分布，因此目标函数维随机过程1：

1. (12 封私信) 如何从深刻地理解随机过程的含义？ - 知乎 （目标函数随机过程中每个变量都是一个随机变量） ↩

$\begin{pmatrix}Y(\mathbf{x^{1}})\\Y(\mathbf{x^{2}})\\\vdots\\Y(\mathbf{x^{n}})\end{pmatrix} \sim N(\mathbf{\mu},C)$ , 取均值为常数$\mathbf{1\mu}\mathbf{1} \in \mathbb{R}^{n \times 1}$，协方差为:

$C=\begin{pmatrix}&cor(Y(\boldsymbol{x^{1}}),Y(\boldsymbol{x^{1}})),&\ldots,&cor(Y(\boldsymbol{x^{1}}),Y(\boldsymbol{x^{n}}))\\&\vdots,&\ddots,&\vdots\\&cor(Y(\boldsymbol{x^{n}}),Y(\boldsymbol{x^{1}})),&\ldots,&cor(Y(\boldsymbol{x^{n}}),Y(\boldsymbol{x^{n}}))\end{pmatrix}$

其中$cor[Y(\boldsymbol{x}^i),Y(\boldsymbol{x}^l)]=exp(-\sum_{j=1}^k\theta_j|x_j^i-x_j^l|^2)$为相关函数/核函数

在特定值下的条件概率为(似然函数)：
$L(\boldsymbol{Y}^1,\boldsymbol{Y}^2,\ldots,\boldsymbol{Y}^n|\mu,\sigma)=\frac{1}{\left(2\pi\sigma^2\right)^{n/2}}exp(-\frac{\Sigma(\boldsymbol{Y}^i-\boldsymbol{\mu})^2}{2\sigma^2}) = \frac{1}{(2\pi\sigma^2)^{n/2}|C|^{1/2}}exp[-\frac{(\boldsymbol{y}-\boldsymbol{1}\mu)^TC^{-1}(\boldsymbol{y}-\boldsymbol{1}\mu)}{2\sigma^2}]$

取对数：$ln(L)=-\frac{n}{2}ln(2\pi)-\frac{n}{2}ln(\sigma^2)-\frac{1}{2}ln|C|-\frac{(\boldsymbol{y}-\boldsymbol{1}\mu)^TC^{-1}(\boldsymbol{y}-\boldsymbol{1}\mu)}{2\sigma^2}$

如何取合适的$\mu,\sigma$使得概率最大？ ==> 求偏导，并分别令偏导数为0，将对应的$\hat{\mu},\hat{\sigma}$带入可得：

$lnL\approx-\frac{n}{2}ln(\hat{\sigma}^2)-\frac{1}{2}ln(|C|)$

因此Kriging的训练(fit)过程就是寻找合适的超参数$\theta$(in $C$)使得$\ln L$最大

Predict

训练后的预测过程目的是寻找合适的$\tilde{\mathbf{y}}$取多少可以让$\ln L$最大

训练后的kriging可以得到$\hat{\mu},\hat{\sigma},\theta_{i}$
假设需要预测的点为$\hat{y}$，将$\mathbf{y}$与$\hat{y}$放在一起，得到$\tilde{\mathbf{y}}=\{\mathbf{y}^T,\hat{y}\}^T$，则协方差矩阵为：

$\tilde{C}=\begin{pmatrix}C&\boldsymbol{r}\\\boldsymbol{r}^T&1\end{pmatrix}$

对应似然函数：$ln(L)=-\frac{n}{2}ln(2\pi)-\frac{n}{2}ln(\hat{\sigma}^2)-\frac{1}{2}ln|\widetilde{C}|-\frac{(\tilde{\boldsymbol{y}}-\mathbf{1}\hat{\mu})^T\widetilde{C}^{-1}(\tilde{\boldsymbol{y}}-\mathbf{1}\hat{\mu})}{2\hat{\sigma}^2}$
只考虑最后一项：$lnL\approx-\frac{\begin{pmatrix}\boldsymbol{y}-\boldsymbol{1}\hat{\mu}\\\hat{y}-\hat{\mu}\end{pmatrix}^T\begin{pmatrix}C&\boldsymbol{r}\\\boldsymbol{r}^T&1\end{pmatrix}^{-1}\begin{pmatrix}\boldsymbol{y}-\boldsymbol{1}\hat{\mu}\\\hat{y}-\hat{\mu}\end{pmatrix}}{2\hat{\sigma}^2}$
中间部分对协方差矩阵根据Partitioned Inverse method求逆

可得：$lnL=-\frac{(\boldsymbol{y}-\boldsymbol{1}\hat{\mu})^{T}A(\boldsymbol{y}-\boldsymbol{1}\hat{\mu})+(\boldsymbol{y}-\boldsymbol{1}\hat{\mu})^{T}B(\hat{y}-\hat{\mu})+(\hat{y}-\hat{\mu})^{T}D(\boldsymbol{y}-\boldsymbol{1}\hat{\mu})+(\hat{y}-\hat{\mu})^{T}E(\hat{y}-\hat{\mu})}{2\hat{\sigma}^{2}}$

==> 对$\hat{y}$求偏导，可得：

$\hat{y}_1(x)=\hat{\mu}+r^TC^{-1}(y-\mathbf{1}\hat{\mu})$

Kernal Function

1.7. Gaussian Processes — scikit-learn 1.7.1 documentation

Kernel operators:

  • sum: $k_{sum}(X, Y) = k_1(X, Y) + k_2(X, Y)$
  • product: $k_{product}(X, Y) = k_1(X, Y) * k_2(X, Y)$
  • exp: $k_{exp}(X, Y) = k(X, Y)^p$
Name Equation 特性
Constant Kernel $k(x_i, x_j) = constant_value \;\forall\; x_i, x_j$
White Kernel $k(x_i, x_j) = noise_level \text{ if } x_i == x_j \text{ else } 0$ 噪声
RBF/Gaussian Kernel $k(x_i, x_j) = \text{exp}\left(- \frac{d(x_i, x_j)^2}{2l^2} \right)$ 平滑
Matérn kernel $k(x_i, x_j) = \frac{1}{\Gamma(\nu)2^{\nu-1}}\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg)^\nu K_\nu\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg),$ 平滑
Rational quadratic kernel $k(x_i, x_j) = \left(1 + \frac{d(x_i, x_j)^2}{2\alpha l^2}\right)^{-\alpha}$ 多个尺度上变化
Dot-Product kernel $k(x_i, x_j) = \sigma_0 ^ 2 + x_i \cdot x_j$ 线性
Exp-Sine-Squared kernel $k(x_i, x_j) = \text{exp}\left(- \frac{ 2\sin^2(\pi d(x_i, x_j) / p) }{ l^ 2} \right)$ 周期性

选择核函数的过程，本质上是在回答一个问题：“我认为我正在建模的这个未知函数具有什么样的内在特性？”

  • 是平滑的吗？（RBF, Matérn）
  • 是周期性的吗？（Exp-Sine-Squared）
  • 是线性的吗？（Dot-Product）
  • 包含噪声吗？（White Kernel）
  • 是在多个尺度上变化的吗？（Rational Quadratic）

通常，最佳实践是通过最大化边际似然函数 (Marginal Likelihood) 来让数据本身“告诉”我们哪个核函数（及其超参数）最合适。然而，一个好的初始选择会大大加速和稳定这个优化过程。

  1. Radial Basis Function / Gaussian Kernel
  • 方程: $k(x_i, x_j) = \text{exp}\left(- \frac{d(x_i, x_j)^2}{2l^2} \right)$
  • 核心假设: 函数是无限可微的，意味着它极其平滑。
  • 超参数:
    • l (length-scale): 长度尺度。决定了函数变化的“剧烈”程度。l 越大，函数越平缓，影响范围越远；l 越小，函数波动越剧烈。
  • 优势:
    • 这是一个非常通用和默认的选择，因为它对平滑函数的建模效果非常好。
    • 只有一个核心超参数 l，相对简单。
  • 如何选择 (适用场景):
    • 当你对函数的具体特性一无所知时，RBF是一个绝佳的起点。
    • 当你相信目标函数是连续且非常平滑的（没有尖锐的突变）。例如，物理系统中温度、压力的平稳变化。

  • 注意事项: RBF的“过度平滑”假设有时可能过于强烈，如果你的函数存在突变或不那么平滑，它可能会掩盖这些细节。

    1. Matérn Kernel
  • 方程: $k(x_i, x_j) = \frac{1}{\Gamma(\nu)2^{\nu-1}}\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg)^\nu K_\nu\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg)$
  • 核心假设: 函数的平滑度是可调节的。
  • 超参数:
    • l: 长度尺度，与RBF中的作用相同。
    • ν (nu): 平滑度参数。这是Matérn核的关键。它控制了函数的可微性。
  • 优势:
    • 灵活性极高。通过调整 ν，Matérn核可以涵盖从非常粗糙到非常平滑的各种函数。
    • 当 ν → ∞ 时，Matérn核等价于RBF核。
    • 当 ν = 1/2 时，它等价于绝对指数核，适用于模拟非常粗糙、不连续的函数。
    • ν = 3/2 和 ν = 5/2 是非常流行的选择，它们假设函数是一次或两次可微的，这在现实世界中比无限可微的假设更为常见。

  • 如何选择 (适用场景):

    • 当RBF的平滑假设太强时，Matérn是更好的选择。
    • 当你需要精确控制函数的平滑度时。在机器学习中，通常将 ν 设为几个固定值之一（如1/2, 3/2, 5/2）进行比较，而不是直接优化它。
    • 对于大多数物理或工程问题，Matérn 3/2 或 5/2 通常比RBF更现实。
    1. Rational Quadratic Kernel
  • 方程: $k(x_i, x_j) = \left(1 + \frac{d(x_i, x_j)^2}{2\alpha l^2}\right)^{-\alpha}$
  • 核心假设: 函数是在多种尺度上变化的特征的叠加。
  • 超参数:
    • l: 长度尺度。
    • α (alpha): 尺度混合参数。决定了不同长度尺度的权重。
  • 优势:
    • 可以看作是无穷多个不同长度尺度的RBF核的加和。
    • 非常适合于建模那些同时包含长期趋势和短期波动的函数。
  • 如何选择 (适用场景):
    • 当你的数据表现出多尺度行为时。例如，股票价格数据，既有长期的牛熊趋势，又有每日的短期波动。
  1. Exp-Sine-Squared Kernel
  • 方程: $k(x_i, x_j) = \text{exp}\left(- \frac{ 2\sin^2(\pi d(x_i, x_j) / p) }{ l^ 2} \right)$
  • 核心假设: 函数具有周期性。
  • 超参数:
    • l: 长度尺度，控制一个周期内函数形状的平滑度。
    • p (periodicity): 周期。决定了函数重复的间隔。
  • 优势:
    • 专门用于对周期性模式进行建模。
  • 如何选择 (适用场景):
    • 当数据明显表现出周期性规律时。例如，季节性温度变化、每日的交通流量、电力消耗等。
    • 注意: 这个核会强制模型在整个定义域内都具有严格的周期性，如果周期性只在局部存在，可能会导致效果不佳。

以下核函数通常不单独使用，而是与其他核函数相加或相乘，以构建更复杂的模型。

  1. White Kernel
  • 方程: $k(x_i, x_j) = noise_level \text{ if } x_i == x_j \text{ else } 0$
  • 核心假设: 每个数据点都包含独立的、不相关的噪声。
  • 超参数:
    • noise_level: 噪声的方差。
  • 优势:
    • 允许模型不必精确穿过每个数据点，从而对带有噪声的观测数据进行建模。
  • 如何选择 (适用场景):
    • 几乎总是需要！ 只要你认为你的观测数据不是完全精确的（这在现实世界中几乎是肯定的），就应该将一个White Kernel加到你的主核函数（如RBF或Matérn）上。
    • k_final = k_RBF + k_White
  1. Constant Kernel
  • 方程: $k(x_i, x_j) = constant_value \;\forall\; x_i, x_j$
  • 核心假设: 控制所有样本点协方差的平均水平。
  • 超参数:
    • constant_value: 信号方差。
  • 优势:
    • 用作其他核函数的缩放因子。
  • 如何选择 (适用场景):
    • 几乎总是与其他核函数相乘使用。它控制了函数输出的平均变化幅度（信号方差）。例如 k_final = C * k_RBF。许多库（如GPy, scikit-learn）会默认将这个常数因子包含在其他核的实现中。
  1. Dot-Product Kernel
  • 方程: $k(x_i, x_j) = \sigma_0 ^ 2 + x_i \cdot x_j$
  • 核心假设: 函数是线性的，可能还有一个偏移量。
  • 超参数:
    • σ_0^2 (sigma_0_squared): 偏移量。控制模型是非齐次（σ_0^2 > 0）还是齐次（σ_0^2 = 0）的。
  • 优势:
    • 可以恢复贝叶斯线性回归。
    • 当与非线性核函数相加时，可以为模型增加一个线性的基准趋势。
  • 如何选择 (适用场景):
    • 当你相信数据主要由一个线性趋势主导时。
    • 当你想构建一个包含线性成分和非线性成分的组合模型时，例如 k_final = k_Linear + k_RBF。

总结与实践建议

  1. 从组合开始: 一个最强大、最通用的起点是 RBF + White Kernel 或 Matérn(ν=5/2) + White Kernel。
    • k(x, x') = C * k_Matérn(x, x') + k_White(x, x')
  2. 观察数据: 在选择之前，先绘制你的数据图。是否存在明显的周期性？是否存在清晰的线性趋势？数据的平滑程度如何？
  3. 组合核函数: 核函数的强大之处在于可以组合。
    • 相加: k1 + k2，表示模型是两种效应的叠加。例如，一个长期线性趋势加上一个周期性波动 k_Linear + k_Periodic。
    • 相乘: k1 * k2，表示一种效应在另一种效应的影响下发生变化。例如，用一个RBF核去乘以一个周期核 k_RBF * k_Periodic，可以建模一个周期性在不同区域平滑度不同的函数。
  4. 模型选择: 如果你不确定，可以尝试几种不同的核函数（或组合），然后通过交叉验证或比较它们的边际似然值来选择最优的一个。

Category

普通克里金 (Ordinary Kriging)
普通克里金是最常用的一种克里金插值方法。它的核心假设是数据的均值在一个局部范围内是未知但恒定的。这意味着它在进行插值时，不会考虑数据中可能存在的全局性趋势或漂移。普通克里金的插值结果是基于样本点之间的空间自相关性，通过变异函数来量化这种关系，并对未知点进行加权平均。

泛克里金 (Universal Kriging)
与普通克里金不同，泛克里金假设数据中存在一个主导的趋势 (trend) 或漂移 (drift)。假设均值不是恒定的，而是随着空间坐标/其他外部变量而变化的函数。这个趋势可以用一个确定性的函数，例如多项式函数来描述。泛克里金会将数据分解为两部分：一个描述趋势的确定性函数和一个包含随机变化的残差项。它首先拟合出数据的趋势，然后对残差进行克里金插值，最后将趋势和插值结果相加得到最终的预测值。因此，当你已知研究区域内存在某种趋势性变化时，例如风向、坡度等，使用泛克里金会更合适。

Co-Kriging(MF)

Multi-fidelity kriging model with large numbers of cheap LF data and small numbers of expensive HF data

MF model分类

“The stochastic Kriging model enables the GCK model to consider the predictive uncertainty from the LF Kriging model at HF sampling points” (Zhou 等, 2020, p. 1885) (pdf)

“There are mainly three kinds of MF surrogate modeling approaches,” (Zhou 等, 2020, p. 1886) (pdf)

hybrid Kriging scaling mode 和 KOH autoregressive model的公式都可以表示为：$\widehat{y}_h(x)=\rho\widehat{y}_l(x)+\widehat{\delta}(x)$，不同的是，缩放因子的确定方法：

  • hybrid Kriging scaling mode：“the scaling factor ρ is determined by minimizing the discrepancy between the scaled LF Kriging model and the HF sampling data” (Zhou 等, 2020, p. 1888) (pdf)
  • KOH autoregressive model：“estimates the scaling factor ρ together with other hyper-parameters of the discrepancy model” (Zhou 等, 2020, p. 1888) (pdf)

“the multi-fidelity modeling approaches can be divided into two types” (Zhou 等, 2020, p. 1887) (pdf)

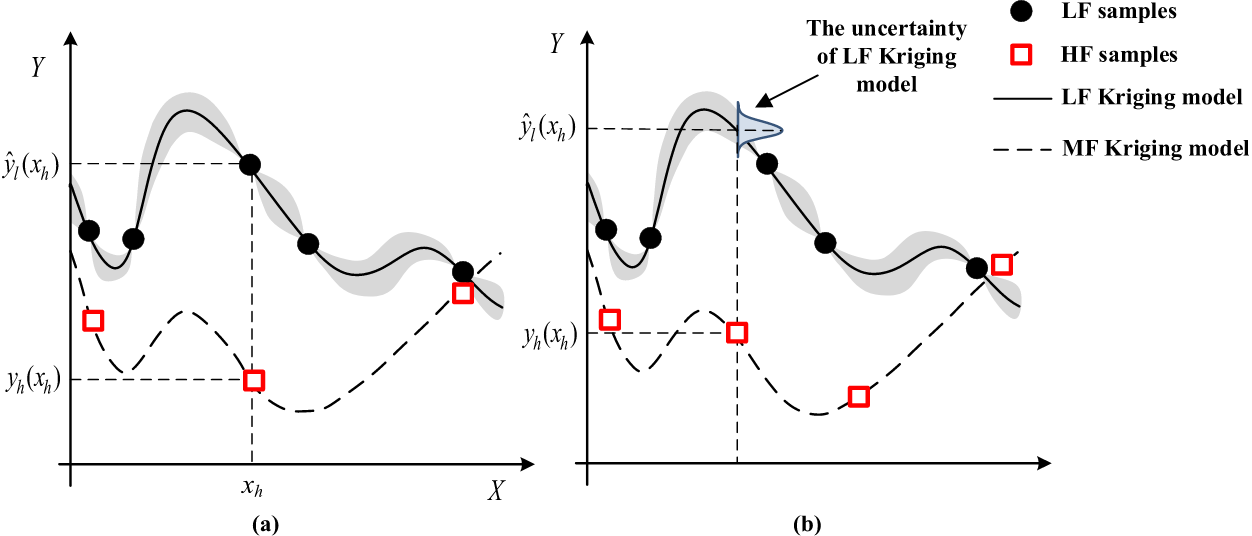
LF and HF sample points （nested or non-nested）

co-kriging方法中通常假设采样点是可分配的，以便于HF和LF的采样点nested，i.e. HF采样点是LF的一个子集，这篇文章提出了“a generalized hierarchical co-Kriging (GCK) surrogate model is proposed for MF data fusion with both nested and non-nested sampling data” (Zhou 等, 2020, p. 1885) (pdf)

  • （左）对于nested data，在HF采样点处HF与LF的差异是确定的，可以使用Kriging近似
  • （右）而对于non-nested，在HF采样点处HF与LF的差异是不确定的，使用stochastic kriging model，差异被建模为$\delta(x)=y_h(x)–\rho y_l(x)=y_h(x)–\rho \widehat{y}_l(x)+\rho \varepsilon_l(x)$

image.png|666

Train process

  • Construct LF dataset $\mathcal{D}_{l}=\{x^{i}_{l},y^{i}_{l}\}_{i=0}^{n_{l}}$和HF dataset $\mathcal{D}_{h}=\{x^{i}_{h},y^{i}_{h}\}_{i=0}^{n_{h}}$
  • Train LF kriging model $Y_{l}(x)$ in $\mathcal{D}_{l}$
  • Construct discrepancy dataset $\mathcal{D}_{d}=\{x^{i}_{h},y^{i}_{h}-Y_{l}(x_{h}^{i})\}_{i=0}^{n_{h}}$ based on LF kriging model and HF dataset
  • Train discrepancy kriging model $\delta(x)=Y_{h}(x)-\lambda Y_{l}(x)$ in $\mathcal{D}_{d}$

Code of kriging

Kriging with different library

cornellius-gp/gpytorch: A highly efficient implementation of Gaussian Processes in PyTorch

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
import math
import torch
import gpytorch
from matplotlib import pyplot as plt

# Training data is 100 points in [0,1] inclusive regularly spaced
train_x = torch.linspace(0, 1, 100)
# True function is sin(2*pi*x) with Gaussian noise
train_y = torch.sin(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * math.sqrt(0.04)

# We will use the simplest form of GP model, exact inference
class ExactGPModel(gpytorch.models.ExactGP):
    def __init__(self, train_x, train_y, likelihood):
        super(ExactGPModel, self).__init__(train_x, train_y, likelihood)
        self.mean_module = gpytorch.means.ConstantMean()
        self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
    
    def forward(self, x):
        mean_x = self.mean_module(x)
        covar_x = self.covar_module(x)
        return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)

# initialize likelihood and model
likelihood = gpytorch.likelihoods.GaussianLikelihood()
model = ExactGPModel(train_x, train_y, likelihood)

# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)
training_iter = 2 if smoke_test else 50

# Find optimal model hyperparameters
model.train()
likelihood.train()

# Use the adam optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.1)  # Includes GaussianLikelihood parameters

# "Loss" for GPs - the marginal log likelihood
mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)
  
for i in range(training_iter):
    # Zero gradients from previous iteration
    optimizer.zero_grad()
    # Output from model
    output = model(train_x)
    # Calc loss and backprop gradients
    loss = -mll(output, train_y)
    loss.backward()
    print('Iter %d/%d - Loss: %.3f   lengthscale: %.3f   noise: %.3f' % (
        i + 1, training_iter, loss.item(),
        model.covar_module.base_kernel.lengthscale.item(),
        model.likelihood.noise.item()
    ))
    optimizer.step()
    
# Get into evaluation (predictive posterior) mode
model.eval()
likelihood.eval()

# Test points are regularly spaced along [0,1]
# Make predictions by feeding model through likelihood
with torch.no_grad(), gpytorch.settings.fast_pred_var():
    test_x = torch.linspace(0, 1, 51)
    print(model(test_x))
    observed_pred = likelihood(model(test_x))
    print(observed_pred)
    
with torch.no_grad():
    # Initialize plot
    f, ax = plt.subplots(1, 1, figsize=(4, 3))

    # Get upper and lower confidence bounds
    lower, upper = observed_pred.confidence_region()
    # Plot training data as black stars
    ax.plot(train_x.numpy(), train_y.numpy(), 'k*')
    # Plot predictive means as blue line
    ax.plot(test_x.numpy(), observed_pred.mean.numpy(), 'b')
    # Shade between the lower and upper confidence bounds
    ax.fill_between(test_x.numpy(), lower.numpy(), upper.numpy(), alpha=0.5)
    ax.set_ylim([-3, 3])
    ax.legend(['Observed Data', 'Mean', 'Confidence'])

1.7. Gaussian Processes — scikit-learn 1.7.1 documentation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C

def f(x):
    return x * np.sin(x)

X_train = np.array([1., 3., 5., 6., 7., 8.]).reshape(-1, 1)
y_train = f(X_train).ravel()

x_pred = np.atleast_2d(np.linspace(0, 10, 1000)).T

kernel = C(1.0, (1e-3, 1e3)) * RBF(10, (1e-2, 1e2))
gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10, alpha=0.1, normalize_y=True)

gp.fit(X_train, y_train)

y_pred, sigma = gp.predict(x_pred, return_std=True)

plt.figure(figsize=(10, 7))
plt.plot(x_pred, f(x_pred), 'r:', label='f(x) = x * sin(x)')
plt.plot(X_train, y_train, 'r.', markersize=10, label='观测数据 (Observations)')
plt.plot(x_pred, y_pred, 'b-', label='预测均值 (Prediction)')
plt.fill_between(x_pred.ravel(), y_pred - 1.96 * sigma, y_pred + 1.96 * sigma,
                 alpha=.2, color='blue', label='95% 置信区间 (Confidence Interval)')
plt.title('高斯过程回归 (Kriging) 示例')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

DKNN

in1311/DKNN

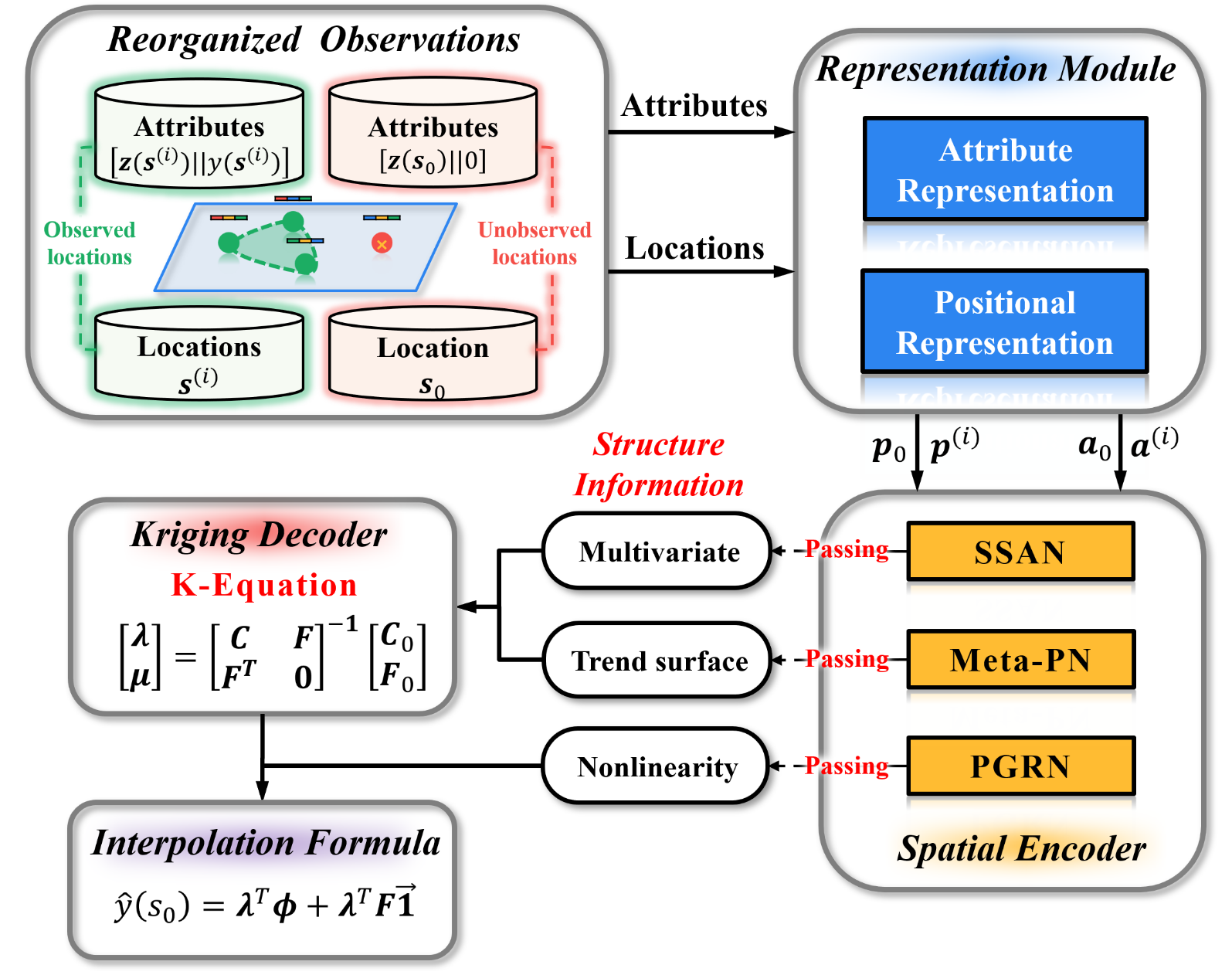
deep kriging neural network 可以用来插值计算

image.png|666

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
def forward(self, input_coods, input_features, input_pe, know_coods, know_features):
    """ 
    Forward process of DKNN

    ----------
    Parameters
    input_coods: Tensor with shape [batch_size, 2]
    input_features: Tensor with shape [batch_size, d_input]
    input_pe: Tensor with shape [batch_size, d_model]
    know_coods: Tensor with shape [know_num, 2]
    know_features: Tensor with shape [know_num, d_input]

    -------
    Returns
    output: Tensor with shape [batch_size, 1]
    out_trend: Tensor with shape [batch_size, 1]
    """

    ##### attribute representation #####
    ae_unknow = self.AttRe(input_features)  # attribute representation of unknown points
    ae_know = self.AttRe(know_features)  # attribute representation of known points

    ##### SSAN #####
    cov_unknow = self.Ssan(ae_unknow, ae_know, input_pe, self.pe_know)  # covariance matrix of unknown points
    cov_know = self.Ssan(ae_know, ae_know, self.pe_know, self.pe_know)  # covariance matrix of known points
    # Zero the diagonal of the matrix cov_know
    cov_know = cov_know - torch.diag_embed(torch.diag(cov_know))
    
    ##### PGRN #####
    known_z = torch.mean(self.Pgrn(ae_know, self.pe_know),-1)  # PGRN output of known points
        
    ##### Meta-PN #####
    trend_know = self.MetaPN(know_coods, self.pe_know)  # trend matrix of known points
    trend_unknow = self.MetaPN(input_coods, input_pe)  # trend matrix of unknown points
    
    ##### kriging decoder and interpolation #####
    output, out_trend = self.kriging_decoder(known_z, cov_know, cov_unknow, trend_unknow, trend_know)
    
    return output, out_trend

def kriging_decoder(self, z_know, cov_know, cov_unknow, trend_unknow, trend_know):
    
    ##### kriging decoder and interpolation  #####
    device = str(cov_know.device) 
    k = trend_know.shape[-1]
    batch_size = cov_unknow.shape[0]

    # Kriging system matrix
    sys_mat_know = torch.zeros(self.known_num + k, self.known_num + k).to(device)
    sys_mat_unknow = torch.zeros(batch_size, self.known_num + k).to(device)

    sys_mat_know[0:self.known_num, 0:self.known_num] = cov_know
    sys_mat_know[0:self.known_num, self.known_num:self.known_num + k] = trend_know
    sys_mat_know[self.known_num:self.known_num + k, 0:self.known_num] = trend_know.T

    sys_mat_unknow[0:batch_size, 0:self.known_num] = cov_unknow
    sys_mat_unknow[0:batch_size, self.known_num:self.known_num + k] = trend_unknow
    
    ##### Solving the K-equation #####
    try:
        sys_mat_know_inv = torch.linalg.inv(sys_mat_know)
    except:
        sys_mat_know_inv = torch.linalg.pinv(sys_mat_know)
    lamda = torch.matmul(sys_mat_unknow, sys_mat_know_inv.T)
    lamda = lamda[:, :-k]
    self.lamda = lamda
    
    ##### Estimated based on interpolation formula #####
    # Residual output
    residual_pre = torch.matmul(lamda, z_know)

    # Trend output
    trend_pre = torch.sum(trend_unknow,-1) / k

    # interpolation output
    prediction = residual_pre + trend_pre

    return prediction, trend_pre

KCN

tufts-ml/kcn-torch A PyTorch Implementation of Kriging Convolutional Networks

Welcome to my other publishing channels