QiYun

Note

Data Structures & Algorithm

Posted on Edited on In
4.2k 15 mins.

Hello 算法 (hello-algo.com)

数据结构

按逻辑结构分类

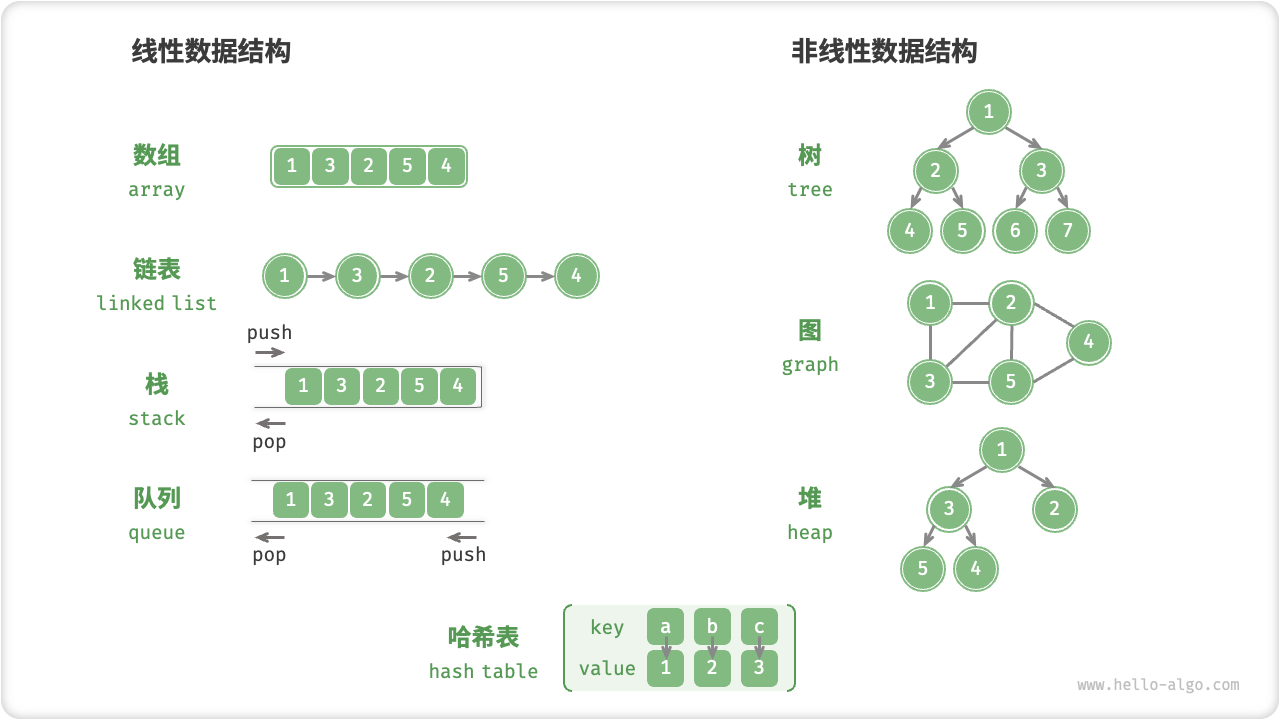
  • 线性结构：数组、链表、队列、栈、哈希表，元素之间是一对一的顺序关系。
  • 树形结构：树、堆、哈希表，元素之间是一对多的关系。
  • 网状结构：图，元素之间是多对多的关系。

image.png|666

按物理结构分类
image.png|666

所有数据结构都是基于数组、链表或二者的组合实现的。例如，栈和队列既可以使用数组实现，也可以使用链表实现；而哈希表的实现可能同时包含数组和链表。

  • 基于数组可实现：栈、队列、哈希表、树、堆、图、矩阵、张量（维度 ≥3 的数组）等。静态数据结构
  • 基于链表可实现：栈、队列、哈希表、树、堆、图等。动态数据结构

计算机编码

  • 整数在计算机中是以补码的形式存储的。在补码表示下，计算机可以对正数和负数的加法一视同仁，不需要为减法操作单独设计特殊的硬件电路，并且不存在正负零歧义的问题。

补码的补码是原码

负数的补码怎么变回原码？ - 知乎 (zhihu.com)

数组

4.1 数组 - Hello 算法 (hello-algo.com)

数组存储在连续的内存空间内，且元素类型相同。这种做法包含丰富的先验信息，系统可以利用这些信息来优化数据结构的操作效率。

数组典型应用

  • 随机访问：如果我们想要随机抽取一些样本，那么可以用数组存储，并生成一个随机序列，根据索引实现样本的随机抽取。
  • 排序和搜索：数组是排序和搜索算法最常用的数据结构。快速排序、归并排序、二分查找等都主要在数组上进行。
  • 查找表：当我们需要快速查找一个元素或者需要查找一个元素的对应关系时，可以使用数组作为查找表。假如我们想要实现字符到 ASCII 码的映射，则可以将字符的 ASCII 码值作为索引，对应的元素存放在数组中的对应位置。
  • 机器学习：神经网络中大量使用了向量、矩阵、张量之间的线性代数运算，这些数据都是以数组的形式构建的。数组是神经网络编程中最常使用的数据结构。
  • 数据结构实现：数组可以用于实现栈、队列、哈希表、堆、图等数据结构。例如，图的邻接矩阵表示实际上是一个二维数组。

当数组非常大时，内存可能无法提供如此大的连续空间 —> 链表的灵活性

数组常用操作

  1. 初始化数组
  2. 访问元素
  3. 插入元素
  4. 删除元素
  5. 遍历数组
  6. 查找元素
  7. 扩容数组

链表

4.2 链表 - Hello 算法 (hello-algo.com)

链表的组成单位是「节点 node」对象。每个节点都包含两项数据：节点的“值”和指向下一节点的“引用”。

1
2
3
4
5
6
7
8
9
10
11
12
# 初始化链表 1 -> 3 -> 2 -> 5 -> 4
# 初始化各个节点
n0 = ListNode(1)
n1 = ListNode(3)
n2 = ListNode(2)
n3 = ListNode(5)
n4 = ListNode(4)
# 构建引用指向
n0.next = n1
n1.next = n2
n2.next = n3
n3.next = n4

通常将头节点当作链表的代称，比如以上代码中的链表可被记做链表 n0 。

数组与链表对比：

数组 链表
存储方式 连续内存空间 分散内存空间
缓存局部性 友好 不友好
容量扩展 长度不可变 可灵活扩展
内存效率 占用内存少、浪费部分空间 占用内存多
访问元素 O(1) O(n)
添加元素 O(n) O(1)
删除元素 O(n) O(1)

image.png|666

链表典型应用

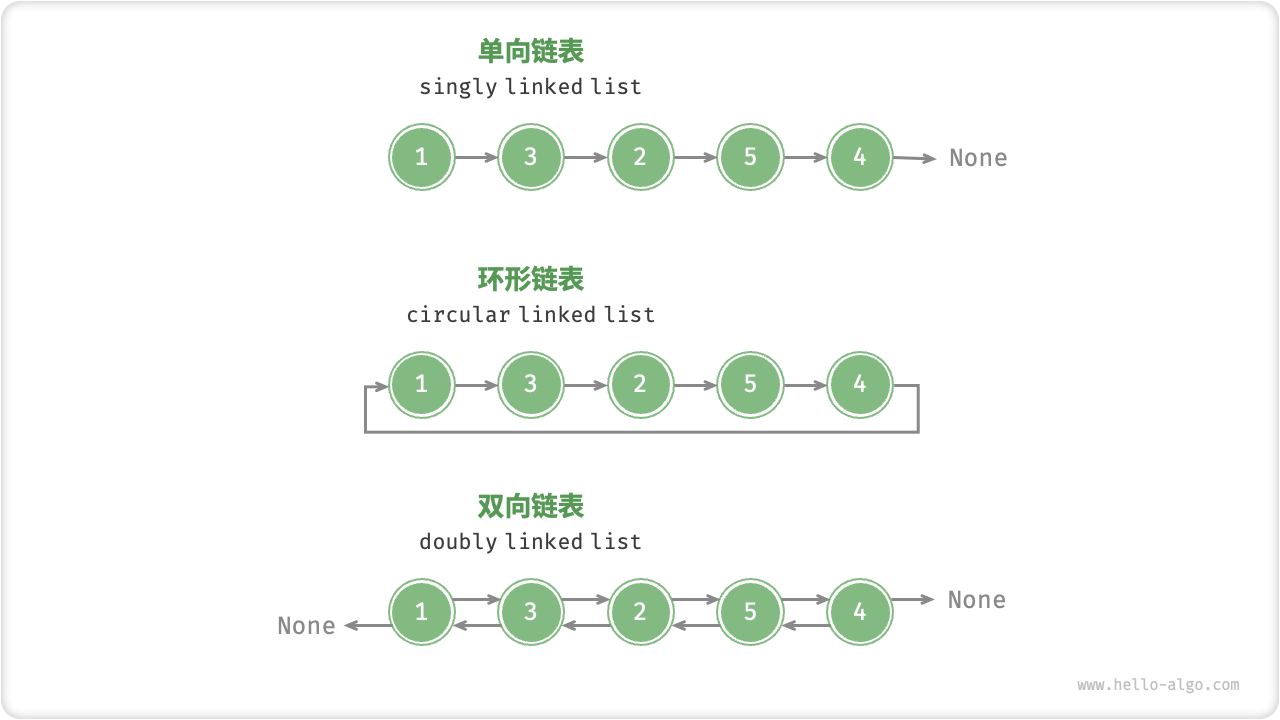
  • 单向链表通常用于实现栈、队列、哈希表和图等数据结构。
  • 双向链表常被用于需要快速查找前一个和下一个元素的场景。
    • 高级数据结构：比如在红黑树、B 树中，我们需要访问节点的父节点，这可以通过在节点中保存一个指向父节点的引用来实现，类似于双向链表。
    • 浏览器历史：在网页浏览器中，当用户点击前进或后退按钮时，浏览器需要知道用户访问过的前一个和后一个网页。双向链表的特性使得这种操作变得简单。
    • LRU 算法：在缓存淘汰算法（LRU）中，我们需要快速找到最近最少使用的数据，以及支持快速地添加和删除节点。这时候使用双向链表就非常合适。
    • 循环链表常被用于需要周期性操作的场景，比如操作系统的资源调度。
    • 时间片轮转调度算法：在操作系统中，时间片轮转调度算法是一种常见的 CPU 调度算法，它需要对一组进程进行循环。每个进程被赋予一个时间片，当时间片用完时，CPU 将切换到下一个进程。这种循环的操作就可以通过循环链表来实现。
    • 数据缓冲区：在某些数据缓冲区的实现中，也可能会使用到循环链表。比如在音频、视频播放器中，数据流可能会被分成多个缓冲块并放入一个循环链表，以便实现无缝播放。

链表常用操作

  1. 初始化链表
  2. 插入节点
  3. 删除节点
  4. 访问节点
  5. 查找节点

列表

「列表 list」是一个抽象的数据结构概念，它表示元素的有序集合，支持元素访问、修改、添加、删除和遍历等操作，无需使用者考虑容量限制的问题。列表可以基于链表或数组实现。

实际上，许多编程语言中的标准库提供的列表都是基于动态数组实现的，例如 Python 中的 list 、Java 中的 ArrayList 、C++ 中的 vector 和 C# 中的 List 等。

在接下来的讨论中，我们将把“列表”和“动态数组”视为等同的概念。

列表常用操作

  1. 初始化列表
  2. 访问元素
  3. 插入与删除元素
  4. 遍历列表
  5. 拼接列表
  6. 排序列表

栈

「栈 stack」是一种遵循先入后出逻辑的线性数据结构。

  • 入栈 push()
  • 出栈 pop()
  • 访问栈顶元素 peek()

通常情况下，我们可以直接使用编程语言内置的栈类。然而，某些语言可能没有专门提供栈类，这时我们可以将该语言的“数组”或“链表”当作栈来使用，并在程序逻辑上忽略与栈无关的操作。
如python：用数组作栈来使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 初始化栈
# Python 没有内置的栈类，可以把 list 当作栈来使用 
stack: list[int] = []

# 元素入栈
stack.append(1)
stack.append(3)
stack.append(2)
stack.append(5)
stack.append(4)

# 访问栈顶元素
peek: int = stack[-1]

# 元素出栈
pop: int = stack.pop()

# 获取栈的长度
size: int = len(stack)

# 判断是否为空
is_empty: bool = len(stack) == 0

队列

「队列 queue」是一种遵循先入先出规则的线性数据结构。顾名思义，队列模拟了排队现象，即新来的人不断加入队列尾部，而位于队列头部的人逐个离开。

  • 将元素添加至队尾 push()
  • 队首元素出队 pop()
  • 访问队首元素 peek()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from collections import deque

# 初始化队列
# 在 Python 中，我们一般将双向队列类 deque 当作队列使用
# 虽然 queue.Queue() 是纯正的队列类，但不太好用，因此不推荐
que: deque[int] = deque()

# 元素入队
que.append(1)
que.append(3)
que.append(2)
que.append(5)
que.append(4)

# 访问队首元素
front: int = que[0];

# 元素出队
pop: int = que.popleft()

# 获取队列的长度
size: int = len(que)

# 判断队列是否为空
is_empty: bool = len(que) == 0

双向队列

  • 将元素添加至队首 push_first()
  • 将元素添加至队尾 push_last()
  • 删除队首元素 pop_first()
  • 删除队尾元素 pop_last()
  • 访问队首元素 peek_first()
  • 访问队尾元素 peek_last() 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from collections import deque

# 初始化双向队列
deque: deque[int] = deque()

# 元素入队
deque.append(2)      # 添加至队尾
deque.append(5)
deque.append(4)
deque.appendleft(3)  # 添加至队首
deque.appendleft(1)

# 访问元素
front: int = deque[0]  # 队首元素
rear: int = deque[-1]  # 队尾元素

# 元素出队
pop_front: int = deque.popleft()  # 队首元素出队
pop_rear: int = deque.pop()       # 队尾元素出队

# 获取双向队列的长度
size: int = len(deque)

# 判断双向队列是否为空
is_empty: bool = len(deque) == 0

哈希表

「哈希表 hash table」，又称「散列表」，它通过建立键 key 与值 value 之间的映射，实现高效的元素查询。

表 6-1 元素查询效率对比

数组 链表 哈希表
查找元素 $O(n)$ $O(n)$ $O(1)$
添加元素 $O(1)$ $O(1)$ $O(1)$
删除元素 $O(n)$ $O(n)$ $O(1)$

哈希表的常见操作包括：初始化、查询操作、添加键值对和删除键值对等

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 初始化哈希表
hmap: dict = {}

# 添加操作
# 在哈希表中添加键值对 (key, value)
hmap[12836] = "小哈"
hmap[15937] = "小啰"
hmap[16750] = "小算"
hmap[13276] = "小法"
hmap[10583] = "小鸭"

# 查询操作
# 向哈希表中输入键 key ，得到值 value
name: str = hmap[15937]

# 删除操作
# 在哈希表中删除键值对 (key, value)
hmap.pop(10583)

在哈希表中，我们将数组中的每个空位称为「桶 bucket」，每个桶可存储一个键值对。因此，查询操作就是找到 key 对应的桶，并在桶中获取 value 。

「负载因子 load factor」是哈希表的一个重要概念，其定义为哈希表的元素数量除以桶数量，用于衡量哈希冲突的严重程度，也常作为哈希表扩容的触发条件。例如在 Java 中，当负载因子超过 0.75 时，系统会将哈希表扩容至原先的 2 倍

哈希冲突解决方法

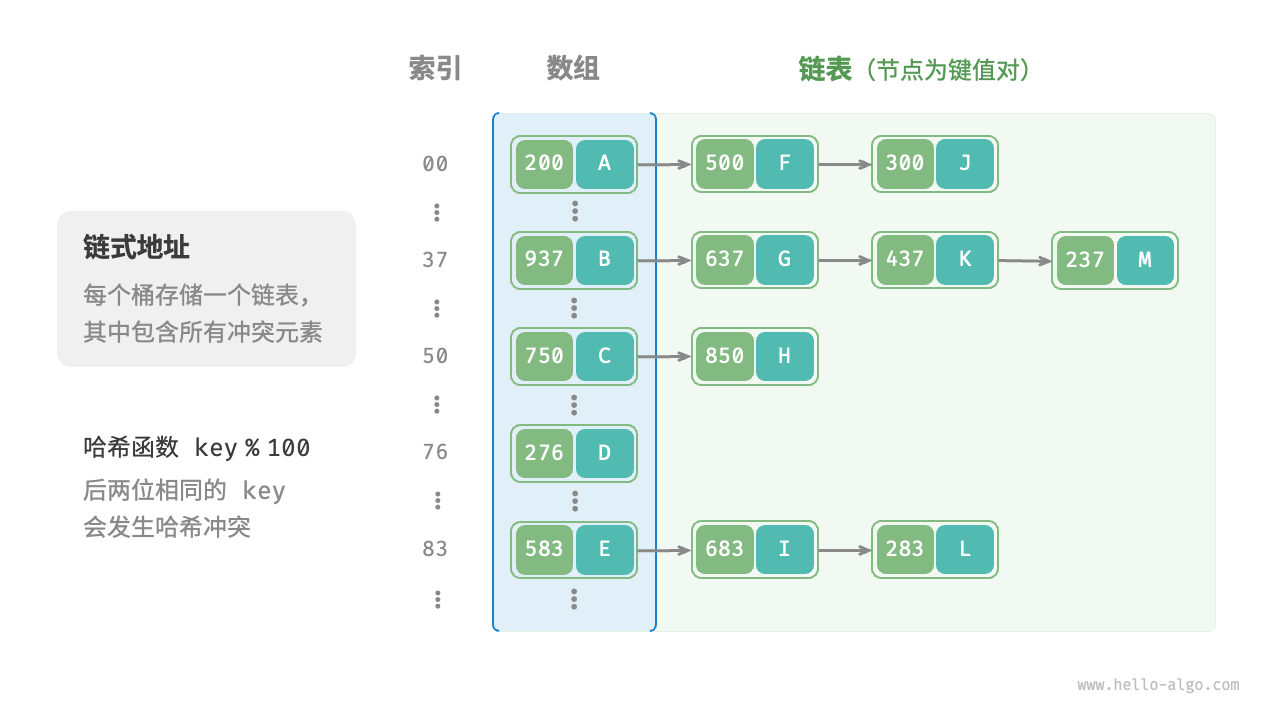
  • 链式地址
    • 占用空间增大：链表包含节点指针，它相比数组更加耗费内存空间。
    • 查询效率降低：因为需要线性遍历链表来查找对应元素。
      image.png|666
  • 开放寻址通过“多次探测”来处理哈希冲突，探测方式主要包括线性探测、平方探测和多次哈希等
    • image.png|666
    • 当发生冲突时，平方探测不是简单地跳过一个固定的步数，而是跳过“探测次数的平方”的步数，即 1,4,9,… 步
    • 多次哈希方法使用多个哈希函数进行探测。

哈希算法

6.3 哈希算法 - Hello 算法

树

「二叉树 binary tree」是一种非线性数据结构，代表“祖先”与“后代”之间的派生关系，体现了“一分为二”的分治逻辑。与链表类似，二叉树的基本单元是节点，每个节点包含值、左子节点引用和右子节点引用。

二叉树的常用术语如图 7-2 所示。

  • 「根节点 root node」：位于二叉树顶层的节点，没有父节点。
  • 「叶节点 leaf node」：没有子节点的节点，其两个指针均指向 None 。
  • 「边 edge」：连接两个节点的线段，即节点引用（指针）。
  • 节点所在的「层 level」：从顶至底递增，根节点所在层为 1 。
  • 节点的「度 degree」：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2 。
  • 二叉树的「高度 height」：从根节点到最远叶节点所经过的边的数量。
  • 节点的「深度 depth」：从根节点到该节点所经过的边的数量。
  • 节点的「高度 height」：从距离该节点最远的叶节点到该节点所经过的边的数量。
  • 请注意，我们通常将“高度”和“深度”定义为“经过的边的数量”，但有些题目或教材可能会将其定义为“经过的节点的数量”。在这种情况下，高度和深度都需要加 1

与链表类似，在二叉树中插入与删除节点可以通过修改指针来实现

常见二叉树类型：

  • 完美二叉树，常被称为「满二叉树」。所有层的节点都被完全填满
  • 完全二叉树，只有最底层的节点未被填满，且最底层节点尽量靠左填充
  • 完满二叉树，除了叶节点之外，其余所有节点都有两个子节点
  • 平衡二叉树，任意节点的左子树和右子树的高度之差的绝对值不超过 1 。

当所有节点都偏向一侧时，二叉树退化为“链表”

二叉树遍历

从物理结构的角度来看，树是一种基于链表的数据结构，因此其遍历方式是通过指针逐个访问节点。然而，树是一种非线性数据结构，这使得遍历树比遍历链表更加复杂，需要借助搜索算法来实现。

时间复杂度$o(n)$ ，空间复杂度$o(n)$

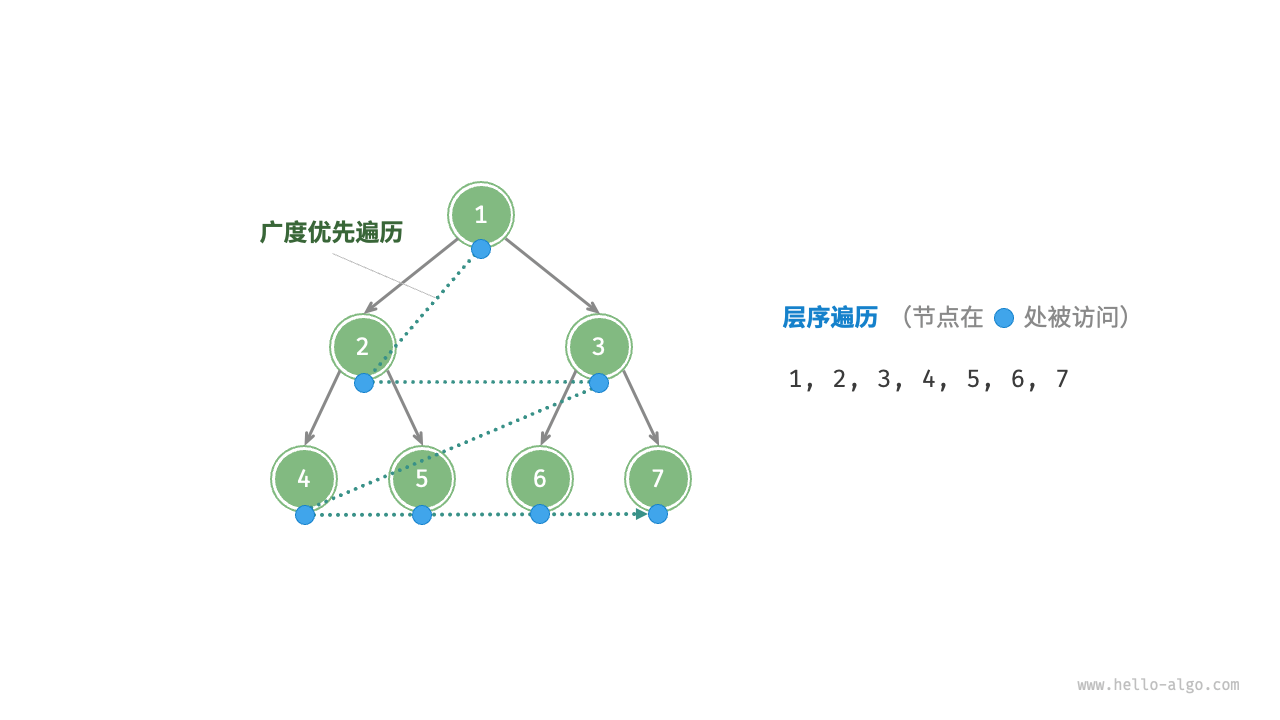
  • 层序遍历，本质上是广度优先搜索 breadth-first search, BFS
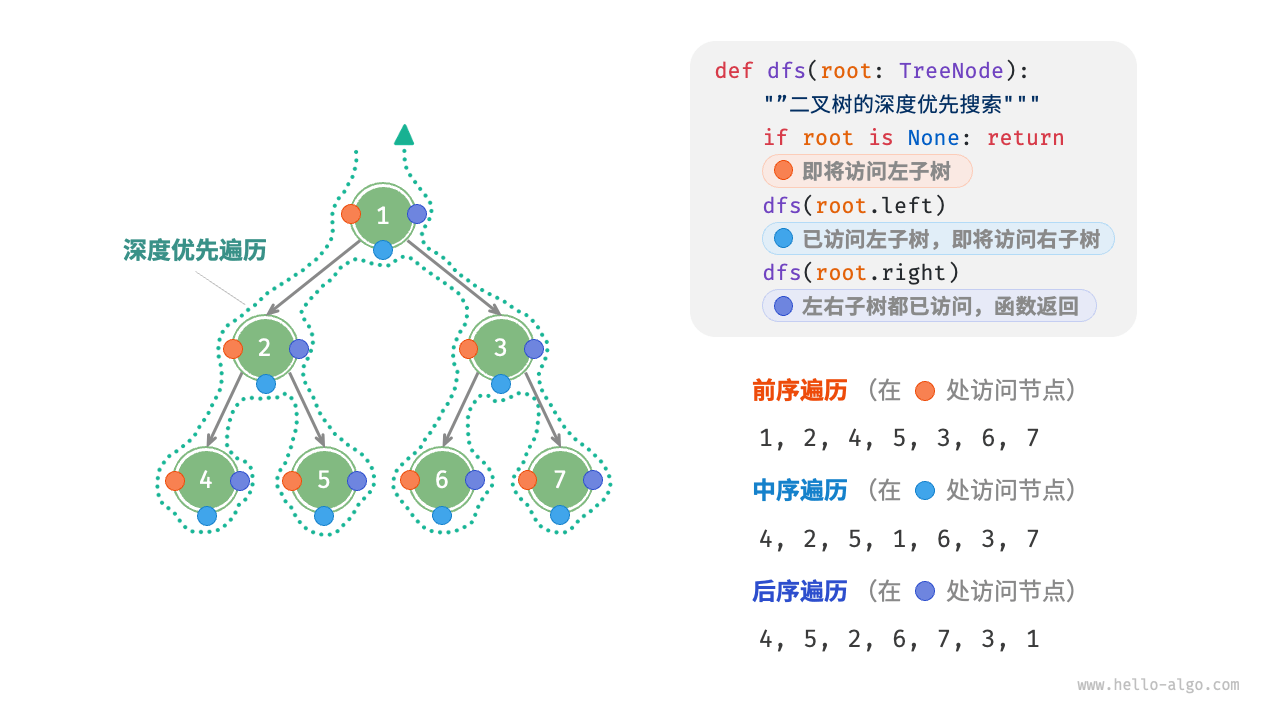
    • image.png|666
  • 前序、中序、后序遍历，本质上是深度优先搜索 depth-first search, DFS
    • image.png|666

二叉搜索树

「二叉搜索树 binary search tree」满足以下条件。

  1. 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
  2. 任意节点的左、右子树也是二叉搜索树，即同样满足条件 1. 。

二叉搜索树的查找操作与二分查找算法的工作原理一致，都是每轮排除一半情况。循环次数最多为二叉树的高度，当二叉树平衡时，使用$o(log n)$时间。
与查找节点相同，插入节点使用$o(log n)$时间。
删除节点操作同样使用$o(log n)$时间，其中查找待删除节点需要$o(log n)$时间，获取中序遍历后继节点需要$o(log n)$时间

二叉搜索树的中序遍历序列是升序的

在多次插入和删除操作后，二叉搜索树可能退化为链表
AVL 树既是二叉搜索树，也是平衡二叉树，同时满足这两类二叉树的所有性质，因此也被称为「平衡二叉搜索树 balanced binary search tree」

  • 由于 AVL 树的相关操作需要获取节点高度，因此我们需要为节点类添加 height 变量。“节点高度”是指从该节点到它的最远叶节点的距离，即所经过的“边”的数量。需要特别注意的是，叶节点的高度为 0 ，而空节点的高度为 −1 。
  • 节点的「平衡因子 balance factor」定义为节点左子树的高度减去右子树的高度，同时规定空节点的平衡因子为 0
  • AVL 树的特点在于“旋转”操作，它能够在不影响二叉树的中序遍历序列的前提下，使失衡节点重新恢复平衡
    • 我们将平衡因子绝对值 >1 的节点称为“失衡节点”。根据节点失衡情况的不同，旋转操作分为四种：右旋、左旋、先右旋后左旋、先左旋后右旋
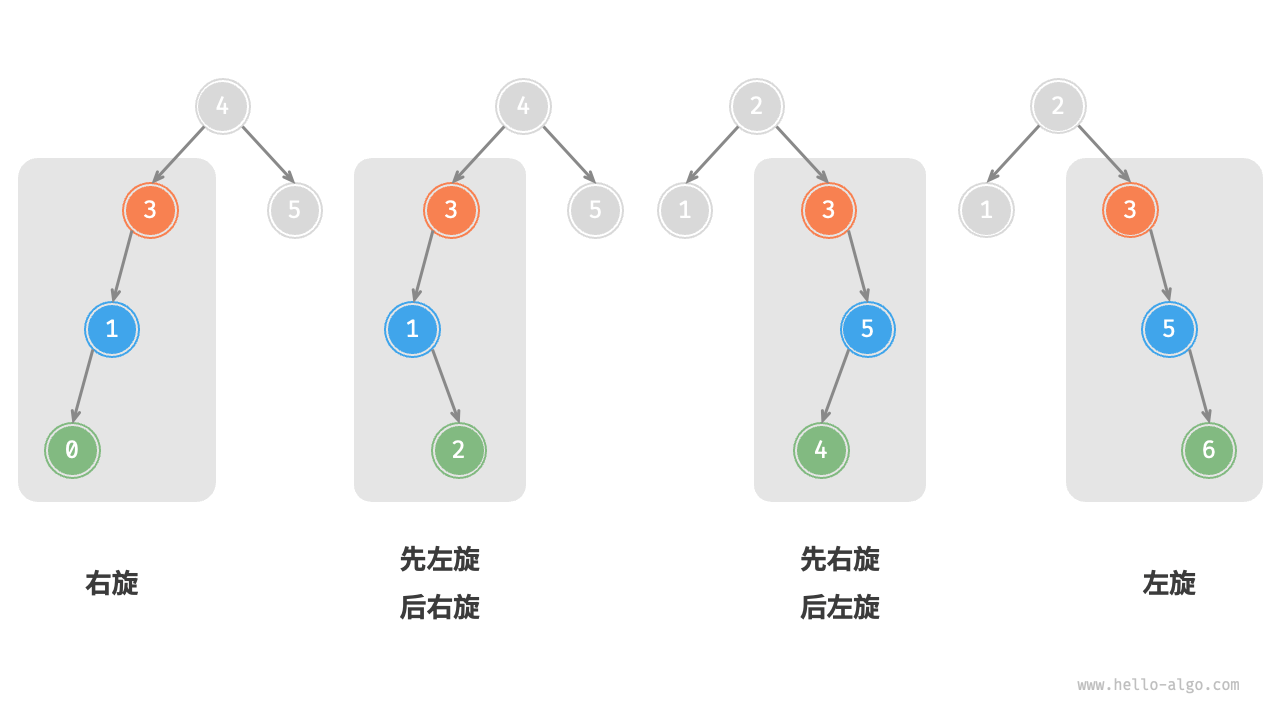
    • image.png|666
  • AVL 树常用操作
    • AVL 树的节点插入操作与二叉搜索树在主体上类似。唯一的区别在于，在 AVL 树中插入节点后，从该节点到根节点的路径上可能会出现一系列失衡节点。因此，我们需要从这个节点开始，自底向上执行旋转操作，使所有失衡节点恢复平衡。
    • 类似地，在二叉搜索树的删除节点方法的基础上，需要从底至顶执行旋转操作，使所有失衡节点恢复平衡
    • AVL 树的节点查找操作与二叉搜索树一致
  • 适用：
    • 组织和存储大型数据，适用于高频查找、低频增删的场景。
    • 用于构建数据库中的索引系统

红黑树在许多应用中比 AVL 树更受欢迎。这是因为红黑树的平衡条件相对宽松，在红黑树中插入与删除节点所需的旋转操作相对较少，其节点增删操作的平均效率更高

堆

「堆 heap」是一种满足特定条件的完全二叉树，主要可分为两种类型

  • 「小顶堆 min heap」：任意节点的值 ≤ 其子节点的值
  • 「大顶堆 max heap」：任意节点的值 ≥ 其子节点的值

图

Python

数据结构

数组：Python 的 list 是动态数组，可以直接扩展

Welcome to my other publishing channels