Reliability：指产品在规定的条件下和规定的时间内，无差错地完成规定任务的概率。
针对产品，依靠数字孪生/CAX技术，使用概率开展研究：
- 实物：实际生产出来的产品，必须了解实验对象（机械/电子/生化…产品），对不同类型产品有哪些故障失效形式
- 失效概率曲线…
- 设备：实验/测量设备，学会如何开展测试实验（Modal Testing）
- 仿真：建模仿真技术，学会软件操作+脚本编写，懂原理更好 (CAX)
- 数学：概率论<贝叶斯>，机器学习/深度学习，可靠性分析基础理论/方法
- 可靠性分析论文(前沿理论) + 可靠性分析项目(实践操作)
权衡：
- 可靠性 ↔ 成本: 可靠性分析增加研发成本，但会降低维修成本
基本概念
专著-北航可靠性与系统工程学院 Book list
crafe.net/files/可靠性科学方法论-康锐.pdf 大致了解以下
电子产品可靠性云评估 CRAFE 2.0 软件平台简介 电子产品可靠性综合评估软件
可靠性数学方法
- 故障数据的统计分析
- 可靠性的理论话语
- 可靠性统计试验
可靠性物理方法 - 故障率——协变量模型
- 故障时间模型
- 性能裕量模型
可靠性逻辑方法 - 功能逻辑方法——可靠性框图
- 故障逻辑方法——故障树分析
可靠性设计方法 - 电子产品降额设计法
- 热设计
- 电磁兼容设计
- 防振动设计
- 余度设计法
概念：
- Failure Mode, Effects & Criticality Analysis (FMECA) 故障模式、影响及危害性分析
- Failure reporting, analysis, and corrective action system （FRACAS） 故障报告、分析与纠正措施系统
- Reliability, Maintainability, and Safety （RMS）： 可靠性R、维修性M、保障性S
三全质量观(全特性、全寿命、全系统)将产品质量特性分为：
- 专用质量特性 SQC
- 通用质量特性 GQC：可靠性、安全性、维修性、测试性、保障性、环境适应性（六性）
系统可靠性设计分析基础
产品故障的度量方法
故障的概率度量
可靠度：产品在规定条件下和规定的时间内，完成规定功能的概率
可靠度函数 $R(t)=P(\xi>t)$
- $\xi$: 产品故障前的工作时间(h)
- t: 规定的时间
$R(t) =\frac{N_{0}-r(t)}{N_{0}}$
- $N_{0}$: 在t=0时刻，规定条件下正常工作的产品数
- $r(t)$: 在0~t时刻产品的累计故障数(假设产品故障后不予修复)
累积故障概率：产品在规定条件下和规定时间内，丧失规定功能的概率
累积故障分布函数 $F(t)=P(\xi\leq t) = \frac{r(t)}{N_{0}}$
显然：$F(t)+R(t) =1$
$F\left(t\right)=\frac{r\left(t\right)}{N_{0}}=\int_{0}^{t}\frac{1}{N_{0}}\frac{dr\left(t\right)}{dt}dt$
故障密度函数：$f\left(t\right)=\frac{1}{N_{0}}\frac{dr\left(t\right)}{dt}$
- $F(t) = \int_{0}^{t} f(t) \, dt$
- $R(t) = \int_{t}^{\infty} f(t) \, dt$
故障率 工作到某时刻尚未故障的产品，在该时刻后单位时间内发生故障的概率
$\lambda\left(t\right)=\lim_{\Delta t\to0}P\left(t\leq\xi\leq t+\Delta t\mid\xi>t\right)$
故障率函数 $\lambda\left(t\right)=\frac{dr\left(t\right)}{N_{s}\left(t\right)dt}$
- 故障率函数的单位为时间间隔单位$dt$的导数($h^{-1}$,$年^{-1}$……)
- $dr\left(t\right)$: t时刻后，$dt$时间内故障的产品数
- $N_{s}(t)$: 到t时刻时，残存的产品数(未故障) $N_{s}(t) = N_{0}-r(t)$
故障率可以近似计算为：$\lambda(t)=\frac{\Delta r(t)}{N_{s}(t)\Delta t}$
- $\Delta r(t)$ : t时刻后，$dt$时间内故障的产品数
- $\Delta t$: 所取得时间间隔
失效率 - 维基百科，自由的百科全书 失效率（英语：Failure rate），也称故障率 Fault
可靠度与故障率、故障密度函数关系：
$\lambda\left(t\right)=\frac{dr\left(t\right)}{N_{s}\left(t\right)dt}=\frac{dr\left(t\right)}{N_{0}\cdot dt}\cdot\frac{N_{0}}{N_{s}\left(t\right)}=\frac{f\left(t\right)}{R\left(t\right)}$
$f\left(t\right)=-\frac{dR\left(t\right)}{dt},$
—> $\lambda\left(t\right)dt=-\frac{dR\left(t\right)}{R\left(t\right)}$
—> $\int_{0}^{t}\lambda\left(t\right)\mathrm{d}t=-\ln R\left(t\right)|_{0}^{t}$
—> $R\left(t\right)=\mathrm{e}^{-\int_{0}^{t}\lambda\left(t\right)dt}$
无法理解😊：当产品寿命服从指数分布时，故障率为常数：$R\left(t\right)=\mathrm{e}^{-\lambda t}$
- 寿命服从指数分布：$f(t)=\lambda e^{-\lambda t}$ ，寿命就是t
- $R(t)=e^{-\lambda t}$
- $\lambda(t) = \frac{f(t)}{R(t)} = \lambda$
故障的时间度量
MTTF:(Mean Time To Failure平均故障前时间)
- 不可修复产品：$T_{TF}=\frac{1}{N_{0}}\sum^{N_{0}}_{i=1}t_{i}$ ，也就是产品故障时间平均值，其中$N_{0}$为所有测试的产品数量
- 当样本足够多$N_{0} \to \infty$，包含所有得故障时间可能 t: ($0 \to \infty$)，则$T_{TF}=\int_{0}^{\infty} tf(t)\, dt = - \int_{0}^{\infty} t \, dR(t) = -[tR(t)]|^{\infty}_{0}+\int_{0}^{\infty} R(t) \, dt = \int_{0}^{\infty} R(t) \, dt$
- 平均故障时间不能唯一确定故障分布的特性，还需要方差辅助描述：$\sigma^{2}=\int_{0}^{\infty} (t-T_{TF})^{2}f(t) \, dt$
TTF: (Time To Failure 故障前时间) 对于有明确故障物理规律的产品，不考虑参数分散性的影响，可给出确定的故障前时间 - 产品重要设计参数S会随时间变化(在产品生命周期中单调且缓慢变化)，超过一定阈值会造成产品故障
- 麦克劳林级数表示：$S\left(t\right)=S_{t=0}+\left(\frac{\partial S}{\partial t}\right)_{t=0}t+\frac{1}{2}\left(\frac{\partial^{2}S}{\partial t^{2}}\right)_{t=0}t^{2}+\cdots$，可简化为$S=S_{0}[1\pm A_{0}(t)^{m}]$，从参数初始值$S_{0}$开始，根据从观察的参数退化数据中得到的可变参数$A_{0}(t),m$，参数上升(+A)或下降(-A)到一定阈值，即会导致产品故障
- 时间$t=\left[\frac{1}{\pm A_{0}}\left(\frac{S-S_{0}}{S_{0}}\right)\right]^{1/m}$ ，假设故障发生的参数阈值为$S_{F}$，则时间t为故障前时间$T_{F}=\left[\frac{1}{\pm A_{0}}\left(\frac{S_{F}-S_{0}}{S_{0}}\right)\right]^{1/m}$
MTBF: (Mean Time Between Failures 平均故障间隔时间) - 可维修产品发生$N_{0}$次故障，每次修复后重新投入使用，每次工作持续时间为$t_{1},t_{2},\dots,t_{N_{0}}$，则MTBF： $T_{BF}=\frac{1}{N_{0}}\sum^{N_{0}}_{i=1}t_{i}=\frac{T}{N_{0}}$，其中T为产品总工作时间(h)
- MTBF与维修效果有关：
- 基本维修：修复后瞬间故障率与故障前瞬间故障率相同
- 完全维修：修复后瞬间故障率与新产品投入使用的故障率相同，对于完全修复的产品，$N_{0}$次故障相当于$N_{0}$个新产品工作到首次故障，因此$T_{BF}=T_{TF}=\int_{0}^{\infty} R(t) \, dt$
MTTR:
故障分为“可修复”和“不可修复”故障，对于“可修复”的系统，我们衡量的是它的“可靠性”和“可用性”，这里的可靠性是指“正常运行的时长；对于“不可修复”的系统或者元器件，我们衡量的是它的可靠性，但这里的可靠性是指“寿命”。
- 不可修复的故障：MTTF、可靠性、寿命 (MTTD = MTTR = 0， 所以 MTBF = MTTF)
- 可修复的故障：MTTR、MTBF、MTTF、可靠性、可用性
可用性的计算公式是Availability = MTBF/(MTBF + MTTR)
Failure Metrics in Depth: MTTR vs. MTBF vs. MTTF MTBF = MTTD + MTTR + MTTF
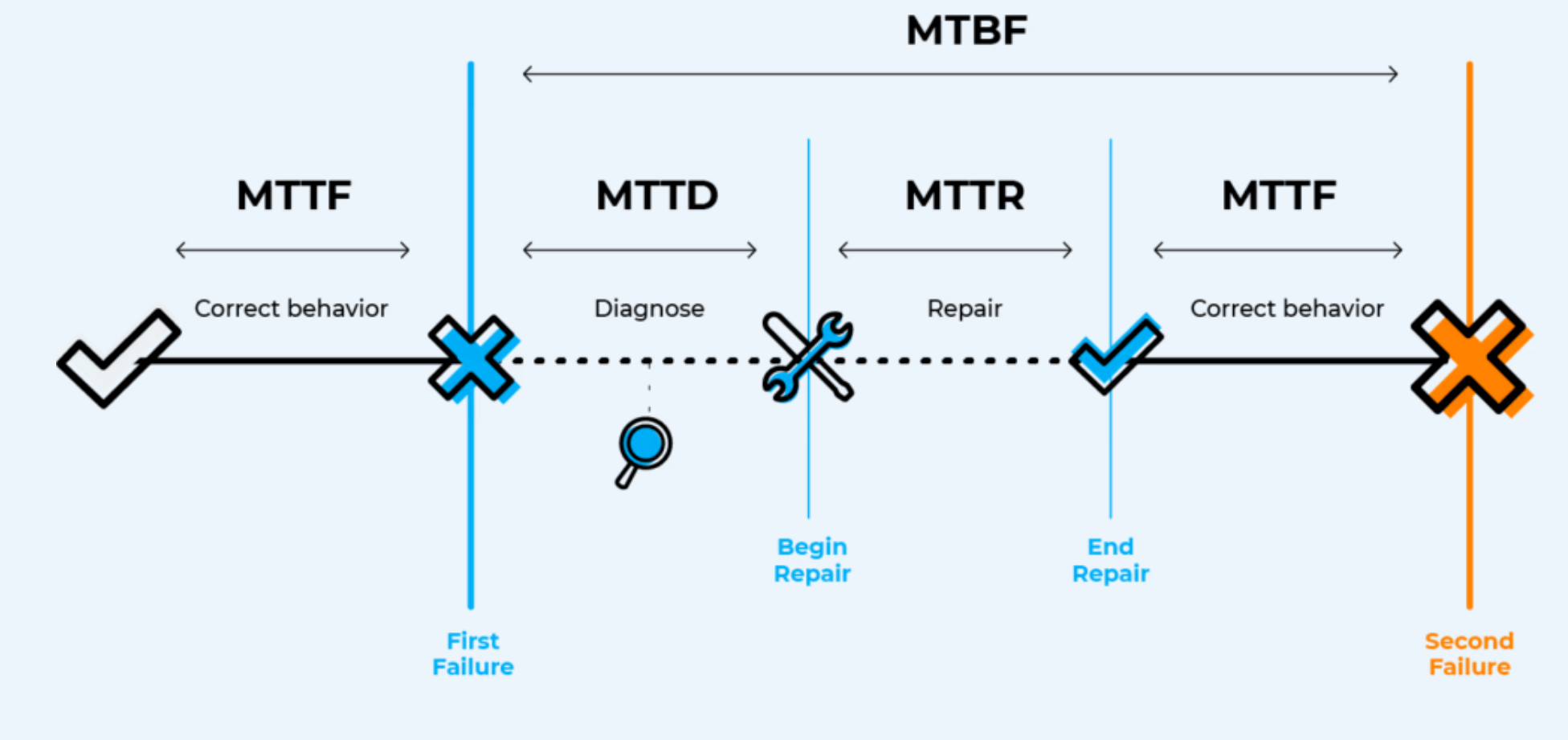
产品故障的规律描述方法
- 不考虑物理因素的统计模型：时间关故障率函数、时间无关故障率函数 (可靠度是时间的函数)
- 考虑物理因素的统计模型：协变模型(可靠度是时间的函数，此外还与一些其他因素相关，如机械结构的几何构型、承受载荷等)，虽然将可靠度函数中的分布参数表达为协变量的函数，但本质仍是统计模型
- 基于物理过程的故障物理模型：应力型故障物理模型、耗损型故障物理模型
不考虑物理因素(故障统计模型)
不足：
- 只能从有限的故障数据样本来推断总体。不能预计某个产品个体的故障，且需要大量故障数据（难获得）。产品总体服从分布，则单个产品发生故障的时间是任意的
- 不能考虑产品实际的环境条件和工作条件的影响
时间无关故障率函数
时间无关故障率函数：寿命服从指数分布，故障率为定值$\lambda(t) = \lambda$
- $F(t)=1-R(t)=1-e^{-\lambda t}$
- $f(t)=\lambda e^{-\lambda t}$
- $T_{TF}=\frac{1}{\lambda}$
- $\sigma^{2}=\frac{1}{\lambda^{2}}$
时间相关故障率函数
时间相关故障率函数:
- 威布尔分布故障率函数：$\lambda(t)=at^{b}$,为了便于计算$\lambda(t)=\frac{\beta}{\theta}\left( \frac{t}{\theta} \right)^{\beta-1}$,($\theta>0,\beta>0,t \geq 0$), 可以描述失效率递增/递减的过程
- $R\left(t\right)=\exp\left[-\int_{0}^{t}\frac{\beta}{\theta}\left(\frac{t^{\prime}}{\theta}\right)^{\beta-1}dt^{\prime}\right]=e^{-\left(t/\theta\right)^{\beta}}$
- $f\left(t\right)=-\frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\frac{\beta}{\theta}\left(\frac{t}{\theta}\right)^{\beta-1}e^{-\left(t/\theta\right)^{\beta}}$
- $\beta$为形状参数，不同的$\beta$值对函数有不同的影响：$\beta <1$时概率密度函数$f(t)$接近指数分布，$\beta \geq 3$时，$f(t)$接近于正态分布，当$1 < \beta < 3$时，$f(t)$为偏锋；当$\beta=1$时，故障率为常数，分布为指数分布$\lambda=\frac{1}{\theta}$; 当$\beta=2$时，$\lambda(t)$呈线性。
- $\theta$为尺度参数，影响分布的均值和散布(离散度)
- $T_{TF} = \theta \Gamma\left( 1+\frac{1}{\beta} \right)$，其中$\Gamma(x)=\int_{0}^{\infty} y^{x-1} e^{-y} \, dy$ 为伽马方程 Γ 函数 - 香蕉空间。通过伽马分布表查询，如果$x>0$，对于超过分布表范围的数据，$\Gamma(x)=(x-1)\Gamma(x-1)$；如果x为整数，则$\Gamma(x)=(x-1)!$
- 方差$\sigma^{2}=\theta^{2}\left\{ \Gamma\left( 1+\frac{2}{\beta} \right)-\left[\Gamma\left( 1+\frac{1}{\beta} \right) \right]^{2} \right\}$
- 给定要求的可靠性水平R：$R(t)=e^{\left( \frac t \theta \right)^{\beta}}=R$ ==>
- 设计寿命$t_{R}=\theta(-\ln R)^{\frac 1 \beta}$ B1寿命(R=0.99)，设计出的产品可能有1%的失效时间 | B.1寿命(R=0.999)，设计出的产品可能有0.1%的失效时间
- 中位数寿命(R=0.5)：$t_{med}=t_{0.5}=\theta(-\ln 0.5)^{\frac 1 \beta}$
- 众数寿命：求解$f(t^{*})=\mathop{\max}\limits_{t \geq 0}f(t)$ ==> $t_{\mathrm{mode}}=\begin{cases}\theta(1-1/\beta)^{1/\beta},&\beta>1\\0,&\beta\leqslant1&\end{cases}$
- 三参数威布尔分布，当存在最小寿命时(假设$t_{0}$前没有发生失效) $t_{0}$被称为位置参数
- 可以通过变换$t’=t-t_{0}$进行转化
- $R\left(t\right)=\exp\left[-\left(\frac{t-t_{0}}{\theta}\right)^{\beta}\right],\quad t\geqslant t_{0}$
- $\lambda\left(t\right)=\frac{\beta}{\theta}\left(\frac{t-t_{0}}{\theta}\right)^{\beta-1},\quad t\geqslant t_{0}$
- $T_{\mathrm{TF}}=t_{0}+\theta\Gamma\left(1+\frac{1}{\beta}\right)$
- $t_{\mathrm{med}}=t_{0}+\theta\left(0.69315\right)^{1/\beta}$
- $t_{d}=t_{0}+\theta(-\ln R)^{1/\beta}$
- 正态分布故障率函数：$f\left(t\right)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left[-\frac{1}{2}\frac{\left(t-\mu\right)^{2}}{\sigma^{2}}\right],\quad-\infty<t<\infty$，适用于疲劳/耗损等故障现象的描述
- $R\left(t\right)=\int_{t}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}\exp\left[-\frac{1}{2}\frac{\left(t^{\prime}-\mu\right)^{2}}{\sigma^{2}}\right]\mathrm{d}t^{\prime}$无有限形式的解，只能通过数值方法
- 转换成标准正态分布$z=\frac{T-\mu}{\sigma}$ 概率密度：$\phi(z)=\frac{1}{\sqrt{2\pi}}\mathrm{e}^{-z^2/2}$ 累积分布$\Phi(z)=\int_{-\infty}^z\phi(z^{\prime})\mathrm{d}z^{\prime}$ 通过查询累积概率值表，得到对应的
- $F\left(t\right)=P\left(T\leqslant t\right)=P\left(\frac{T-\mu}{\sigma}\leqslant\frac{t-\mu}{\sigma}\right)=P\left(z\leqslant\frac{\iota-\mu}{\sigma}\right)=\Phi\left(\frac{\iota-\mu}{\sigma}\right)$
- $R\left(t\right)=1-\Phi\left(\frac{\iota-\mu}{\sigma}\right)$ $F\left(t\right)=\Phi\left(\frac{\iota-\mu}{\sigma}\right)$
- 故障率函数为增函数$\lambda\left(t\right)=\frac{f\left(t\right)}{R\left(t\right)}=\frac{f\left(t\right)}{1-\Phi\left[\left(t-\mu\right)/\sigma\right]}$
- $R\left(t\right)=\int_{t}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}\exp\left[-\frac{1}{2}\frac{\left(t^{\prime}-\mu\right)^{2}}{\sigma^{2}}\right]\mathrm{d}t^{\prime}$无有限形式的解，只能通过数值方法
- 对数正态分布：一个随机变量T的$T_{TF}$服从正态分布，则其对数也服从正态分布$f\left(t\right)=\frac{1}{\sqrt{2\pi}st}\exp\left[-\frac{1}{2s^{2}}\left(\ln\frac{t}{t_{med}}\right)^{2}\right],\quad t\geqslant0$
- s为形状参数，$t_{med}$为位置参数，失效的中位时间，t只能为正值，因此相较于正态分布更适合于描述故障过程。常常是服从威布尔分布的数据也服从对数正态分布
- $T_{TF}=t_{med}exp\left(s^{2}/2\right)$
- $\sigma^{2}=t_{med}^{2}exp\left(s^{2}\right)\left[exp\left(s^{2}\right)-1\right]$
- $t_{mode}=\frac{t_{med}}{exp\left(s^{2}\right)}$
- $F\left(t\right)=P\left(T\leqslant t\right)=P\left(\frac{\ln T-\ln t_{med}}{s}\leqslant\frac{\ln t-\ln t_{med}}{s}\right)=P\left(z\leqslant\frac{1}{s}\ln \frac{t}{t_{med}}\right)=\Phi\left(\frac{1}{s} \ln \frac{t}{t_{med}}\right)$
- $R(t)=1-\Phi\left( \frac{1}{s}\ln \frac{t}{t_{med}} \right)$
考虑物理因素的统计模型
故障协变模型
- 比例故障模型：不同产品的故障率成比例，并且不随时间发生变化。指数分布or威布尔分布
- 位置-尺度模型：正态分布or对数正态分布
故障物理模型
故障物理模型：
- 过应力型故障
- 静态应力-强度模型：可靠度是常数
- 随机应力x+固定强度y
- 固定应力x+随机强度y
- 随机应力x+随机强度y statistics - Finding probability $P(X<Y)$ - Mathematics Stack Exchange
- 指数分布
- 正态分布
- 对数正态分布
- 动态应力-强度模型：动态可靠度
- 周期载荷：作用产品n次
- 随机载荷：作用时间是随机的，且单位时间内的载荷作用次数服从泊松分布
- 随机恒定载荷和强度
- 静态应力-强度模型：可靠度是常数
- 耗损型故障
- 一般数学模型
- 基础模型/经典模型：
- 阿伦尼斯模型
- 艾林模型
- 损伤累积模型
- 故障机理竞争模型
- 典型模型：
- 电迁移模型
- 时间相关的介质击穿模型
- 腐蚀模型