Time Series Generation | Papers With Code
- 生成样本,解决样本不足的问题
Review
GAN
Generative Adversarial Networks in Time Series: A Systematic Literature Review
- Autoregressive (AR) to forecast data point of time series:$x_{t+1} = c + \theta_1x_t + \theta_2x_{t-1} + \epsilon$。然而其内在是确定性的由于没有在未来系统状态的计算中引入随机性
- Generative Methods:
- Autoencoder (AE)
- variational autoencoders (VAEs)
- recurrent neural network (RNN)
- GAN is inherent instability, suffer from issues:
- non-convergence, A non-converging model does not stabilize and continuously oscillates, causing it to diverge.
- diminishing/vanishing gradients, Diminishing gradients prevent the generator from learning anything, as the discriminator becomes too successful.
- mode collapse. Mode collapse is when the generator collapses, producing only uniform samples with little to no variety.
- 没有比较好的评价指标
GAN Model task: 生成器G要最大化判别器D的错误率,而判别器D则是要最小化其错误率
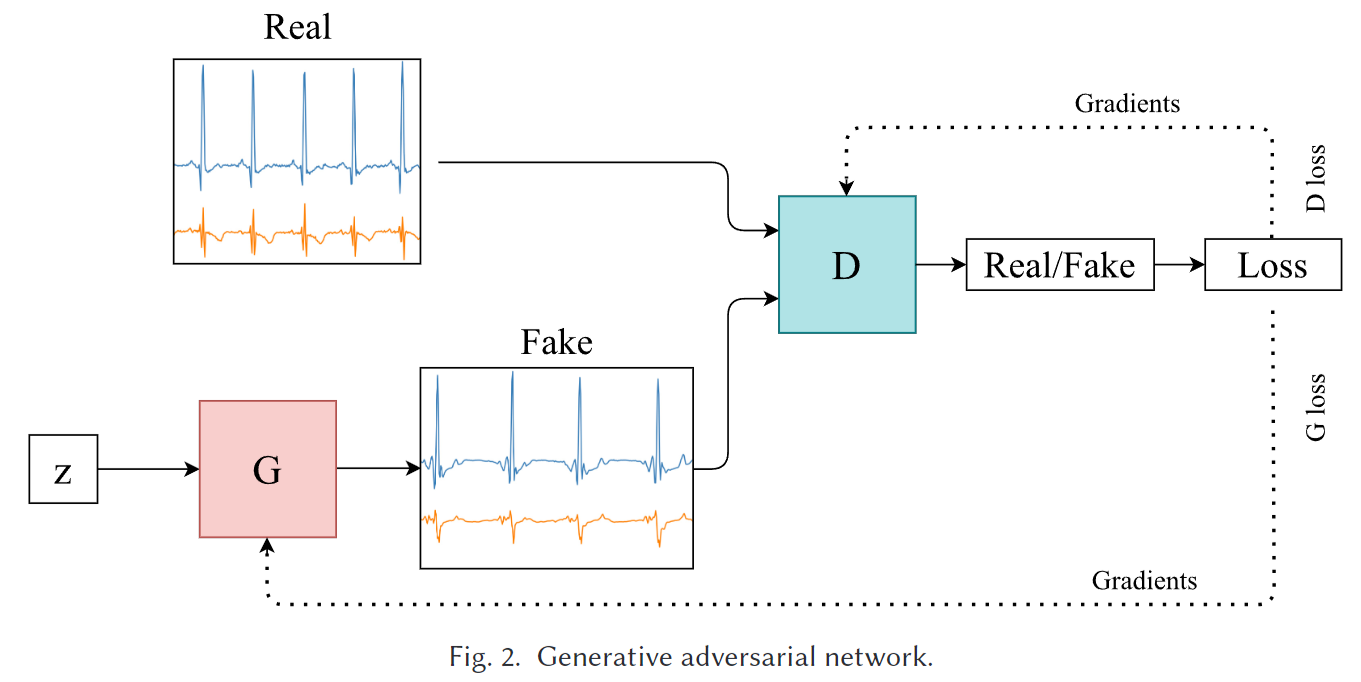
应用:
- Data Augumentation
- Imputation
- Denoising
- Anomaly Detection异常检测
Diffusion
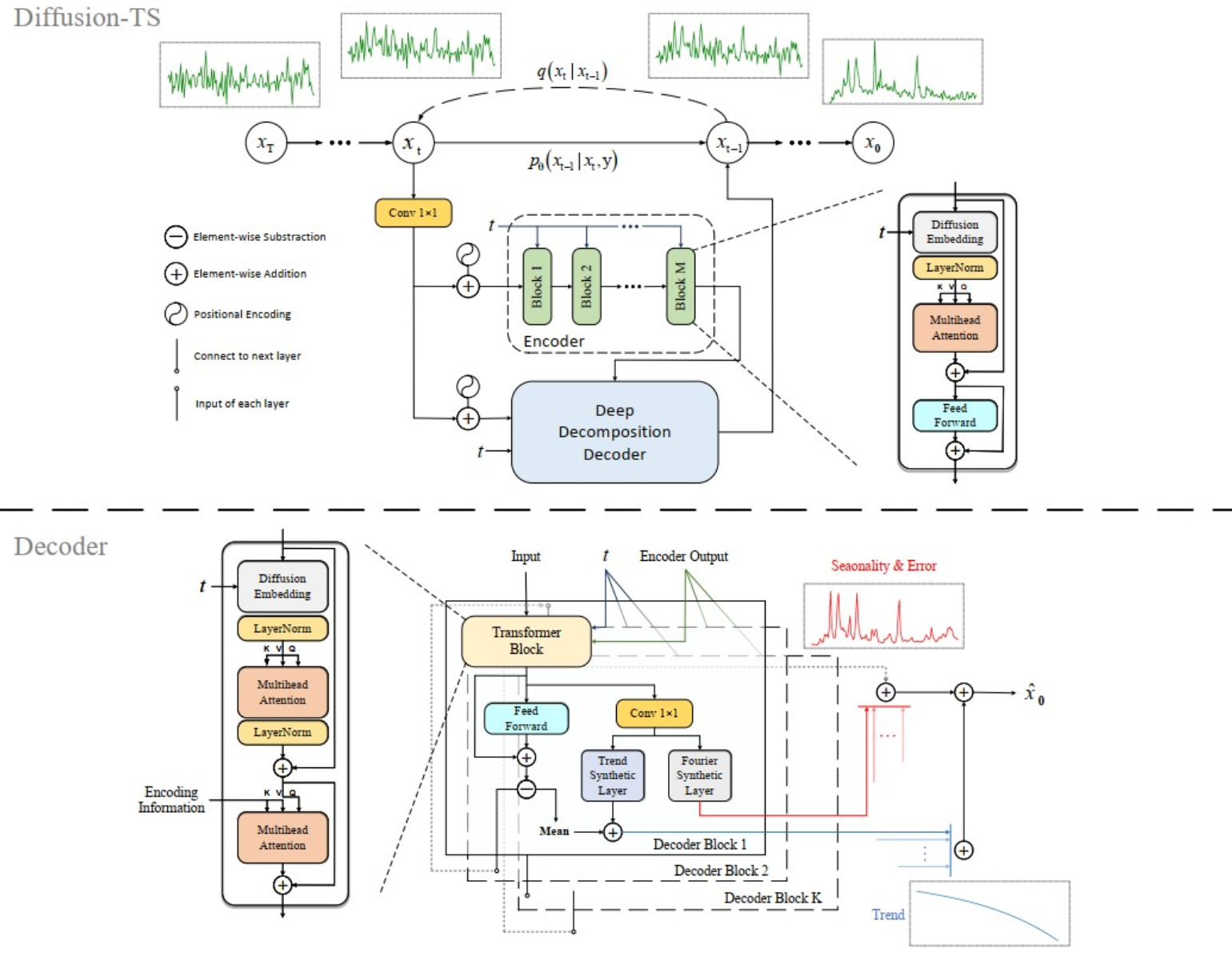
Diffusion TS 2024
Diffusion + Transformer
UNCONDITIONAL TIME SERIES GENERATION,输入的是噪声数据 img = torch.randn(shape, device=device)
CONDITIONAL TIME SERIES GENERATION:这里的条件代表的也是time series(缺失部分数据)
- Imputation 补全
- Forecasting 预测
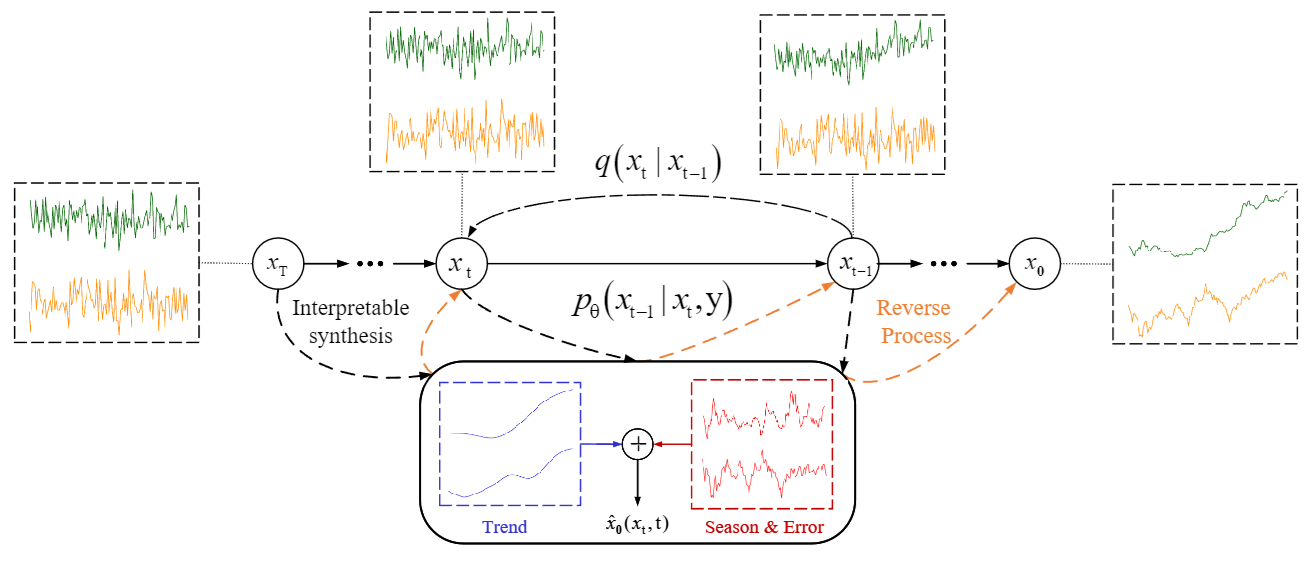
时间序列数据可分为:
- 趋势项 Trend+周期项 Seasonality+误差项 Error
- $x_j=\zeta_j+\sum_{i=1}^ms_{i,j}+e_j,\quad j=0,1,\ldots,\tau-1,$
- $\hat{x}_0(x_t,t,\theta)=V_{tr}^t+\sum_{i=1}^DS_{i,t}+R$
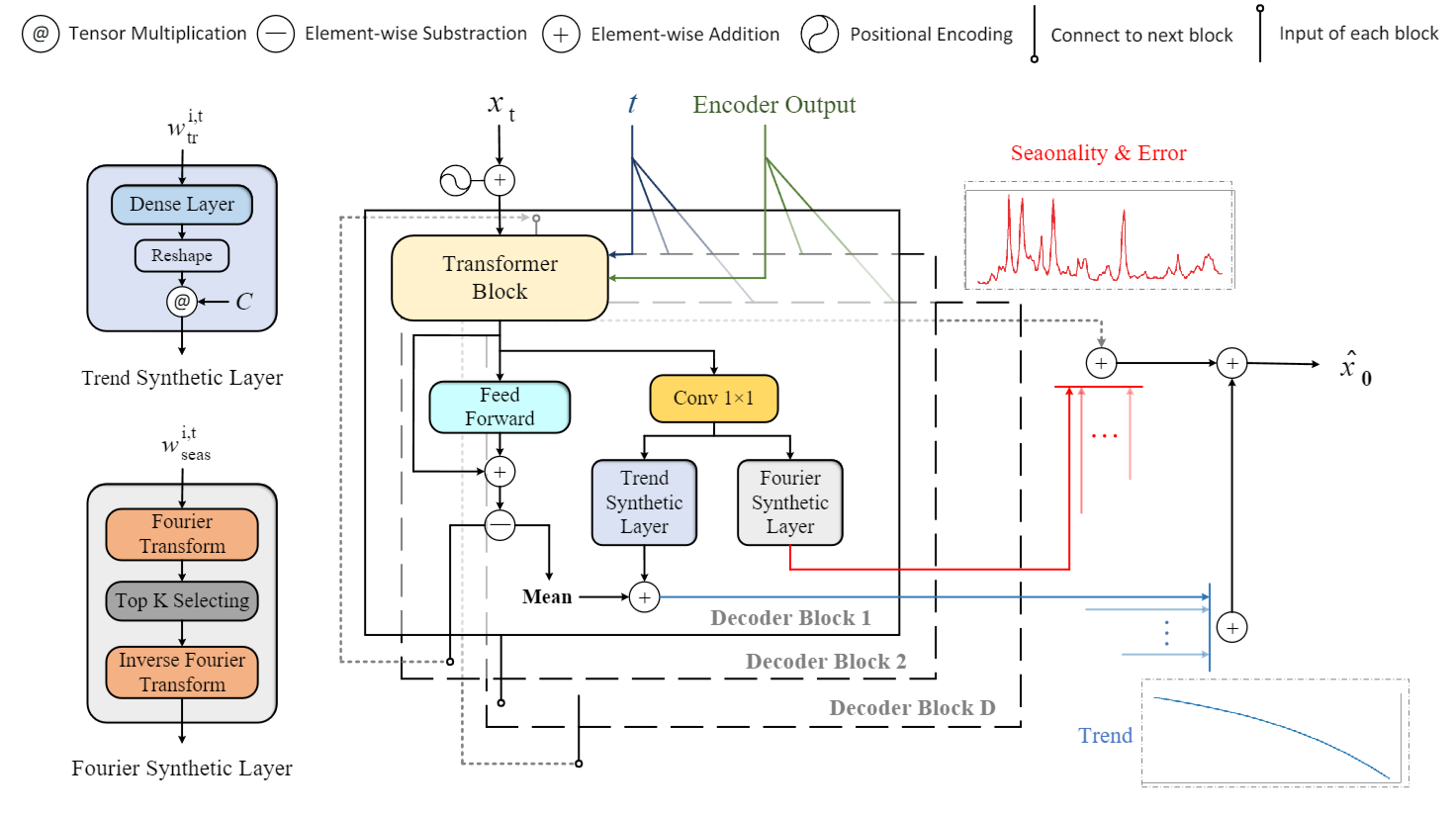
Trend: $V_{tr}^t=\sum_{i=1}^D(\boldsymbol{C}\cdot\mathrm{Linear}(w_{tr}^{i,t})+\mathcal{X}_{tr}^{i,t}),\quad\boldsymbol{C}=[1,c,\ldots,c^p]$
- D 代表由 D 个 Decoder block
- $\mathcal{X}_{tr}^{i,t}$ 是 i-th 个 Decoder block 输出的均值,趋势项加上这个可以让其在y轴上下移动,该项的累加在代码中并不是简单的求和, 而是通过一个conv1d来动态调整求和时的权重,此外还会加上最后一个decoder block输出的均值
- C is the matrix of powers of vector $c=\frac{[0,1,2,\dots,\tau-2,\tau-1]^{T}}{\tau}$ $\tau$ is the time series length
- $y=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\dots+a_{p}x^{p}$ ,
- 系数a即网络的输出$\mathrm{Linear}(w_{tr}^{i,t})$
- $x,x^{2},x^{3}\dots,x^{p}$ 本质上是通过C来表示
- $y=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\dots+a_{p}x^{p}$ ,
- P is a small degree (p=3) to model low frequency behavior p=3代表用3阶来拟合趋势项已经足够
TrendBlock:
- Input: input $w_{tr}^{i,t}$
- Output: trend_vals $\boldsymbol{C}\cdot\mathrm{Linear}(w_{tr}^{i,t})$
1 | ###### TrendBlock ###### |
Seasonality: $S_{i,t}=\sum_{k=1}^{K}A_{i,t}^{\kappa_{i,t}^{(k)}}\left[\cos(2\pi f_{\kappa_{i,t}^{(k)}}\tau c+\Phi_{i,t}^{\kappa_{i,t}^{(k)}})+\cos(2\pi\bar{f}_{\kappa_{i,t}^{(k)}}\tau c+\bar{\Phi}_{i,t}^{\kappa_{i,t}^{(k)}})\right],$
- Amplitude $A_{i,t}^{(k)}=\left|\mathcal{F}(w_{seas}^{i,t})_{k}\right|$
- Phase $\Phi_{i,t}^{(k)}=\phi\left(\mathcal{F}(w_{seas}^{i,t})_{k}\right)$
- $\mathcal{F}$ is the discrete Fourier transform
- $\kappa_{i,t}^{(1)},\cdots,\kappa_{i,t}^{(K)}=\arg\text{TopK}\\k\in\{1,\cdots,\lfloor\tau/2\rfloor+1\}$ 选择 top K 的幅值和相位,K is a hyperparameter
- $f_{k}$ represents the Fourier frequency of the corresponding index k, $\bar{f}_{k}$ 为 $f_{k}$ 的共轭
- $\tau c=\tau \cdot\frac{[0,1,2,\dots,\tau-2,\tau-1]^{T}}{\tau}=[0,1,2,\dots,\tau-2,\tau-1]^{T}$
FourierLayer:
- Input: x $w_{seas}^{i,t}$
- Output: x_time $S_{i,t}$
x_freq, x_freq.conj()是$\mathcal{F}(w_{seas}^{i,t})_{k}$ 和其共轭,通过abs 和 angle 得到幅值和相位f, -fis $f_{k}$ and $\bar{f}_{k}$
1 | ###### FourierLayer ###### |
Error: R is the output of the last decoder block, which can be regarded as the sum of residual
periodicity and other noise. 代码中的R为最后一个decoder block输出减去其平均值,并将平均值加到趋势项中,让周期项不包含任何的y轴方向信息
时间序列数据被表示为 $\hat{x}_0(x_t,t,\theta)=V_{tr}^t+\sum_{i=1}^DS_{i,t}+R$,然后通过DDPM来直接预测原始样本,反向生成过程被表示为:$x_{t-1}=\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}\hat{x}_0(x_t,t,\theta)+\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t+\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\beta_tz_t,$
- $z_t\sim\mathcal{N}(0,\mathbf{I}), \alpha_t=1-\beta_t\text{ and }\bar{\alpha}_t=\prod_{s=1}^t\alpha_s$
损失函数:
时域+FFT频域监督:$\mathcal{L}_\theta=\mathbb{E}_{t,x_0}\left[w_t\left[\lambda_1|x_0-\hat{x}_0(x_t,t,\theta)|^2+\lambda_2|\mathcal{F}\mathcal{FT}(x_0)-\mathcal{FFT}(\hat{x}_0(x_t,t,\theta))|^2\right]\right]$
- $\mathcal{L}_{simple}=\mathbb{E}_{t,x_{0}}\left[w_{t}|x_{0}-\hat{x}_{0}(x_{t},t,\theta)|^{2}\right],\quad w_{t}=\frac{\lambda\alpha_{t}(1-\bar{\alpha}_{t})}{\beta_{t}^{2}}$
- 其中权重被设置为当在 small t 时权重变小,让网络集中在更大的 diffusion step t(噪声较多的时候)
- 由 $x_t=\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon.$,随着t的增大,$\alpha_{t}$ 在逐渐变小
上述过程为无条件 time series generation,本文还描述了conditional extensions of Diffusion-TS,即the modeled $x_{0}$ 以 targets y 为条件。
1 | # 环境配置 |
1 | # train with stocks dataset with gpu 0 |
GANs
RGANs Most⭐2017
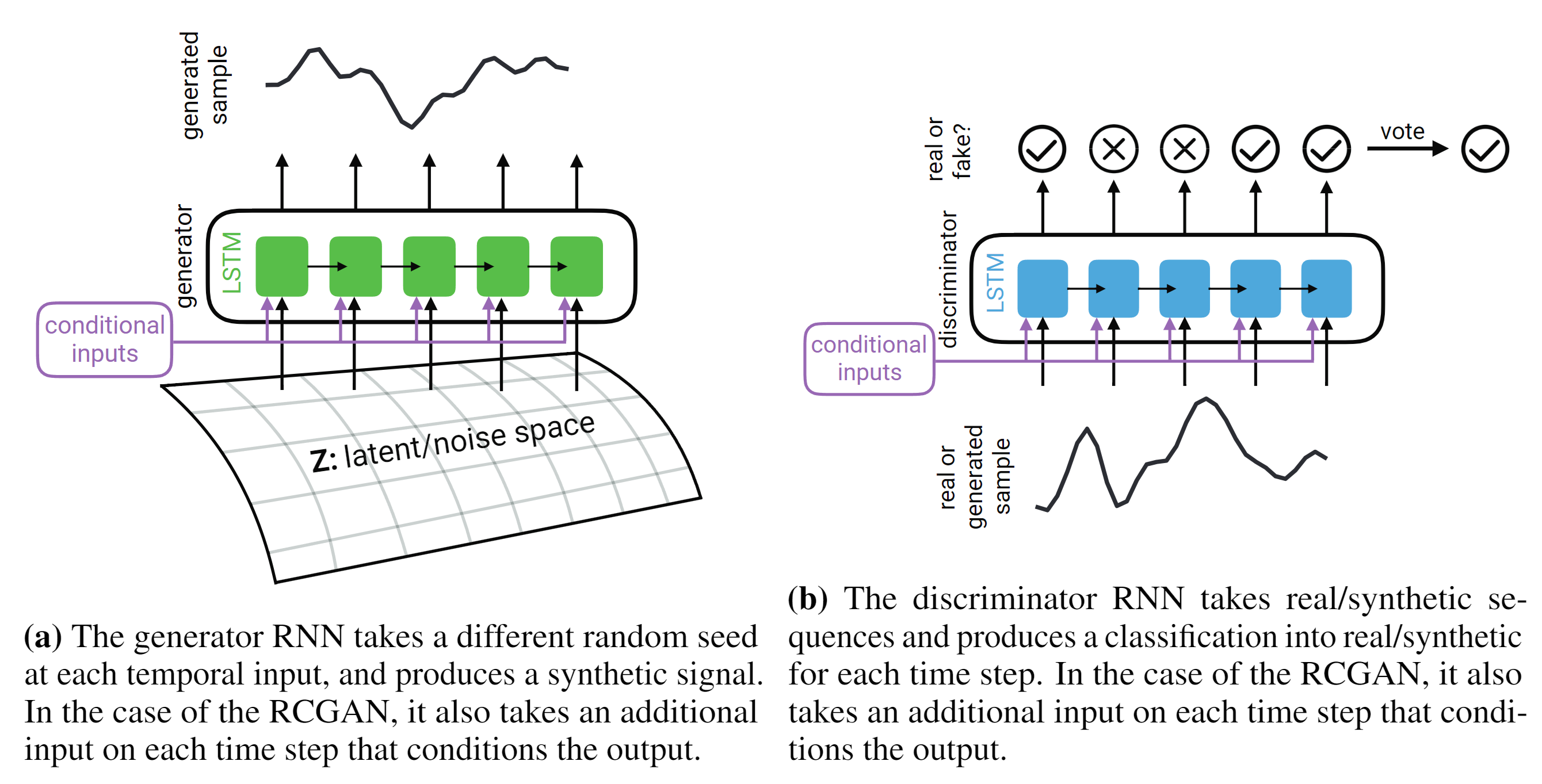
SigCGANs
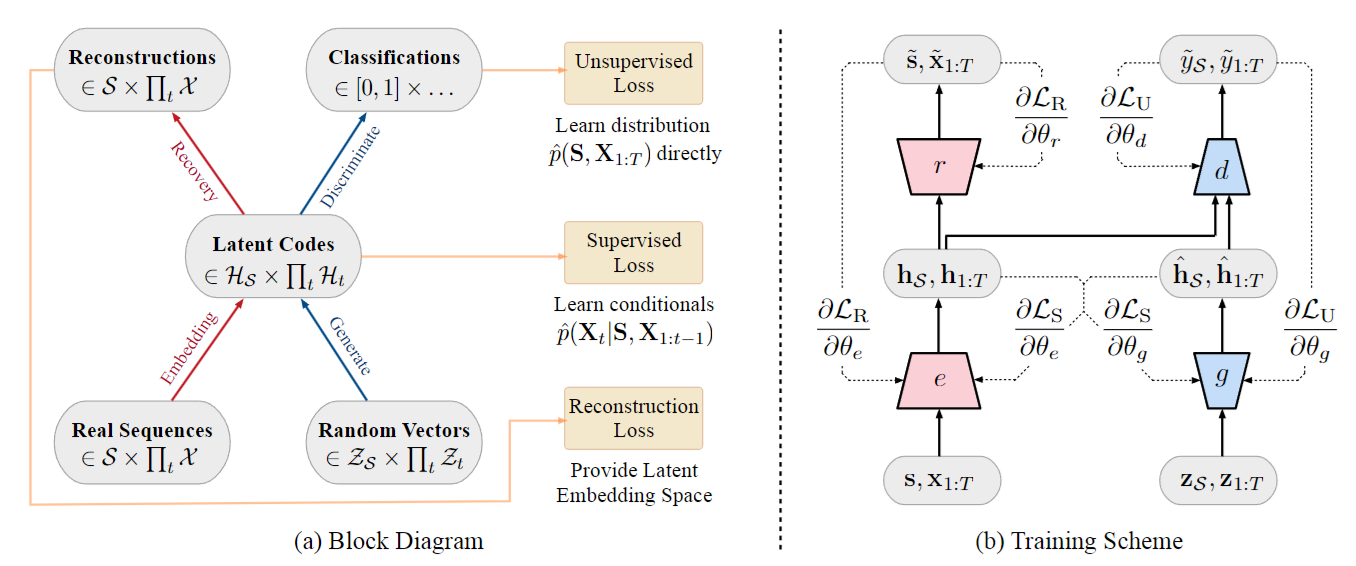
TimeGAN
VAE
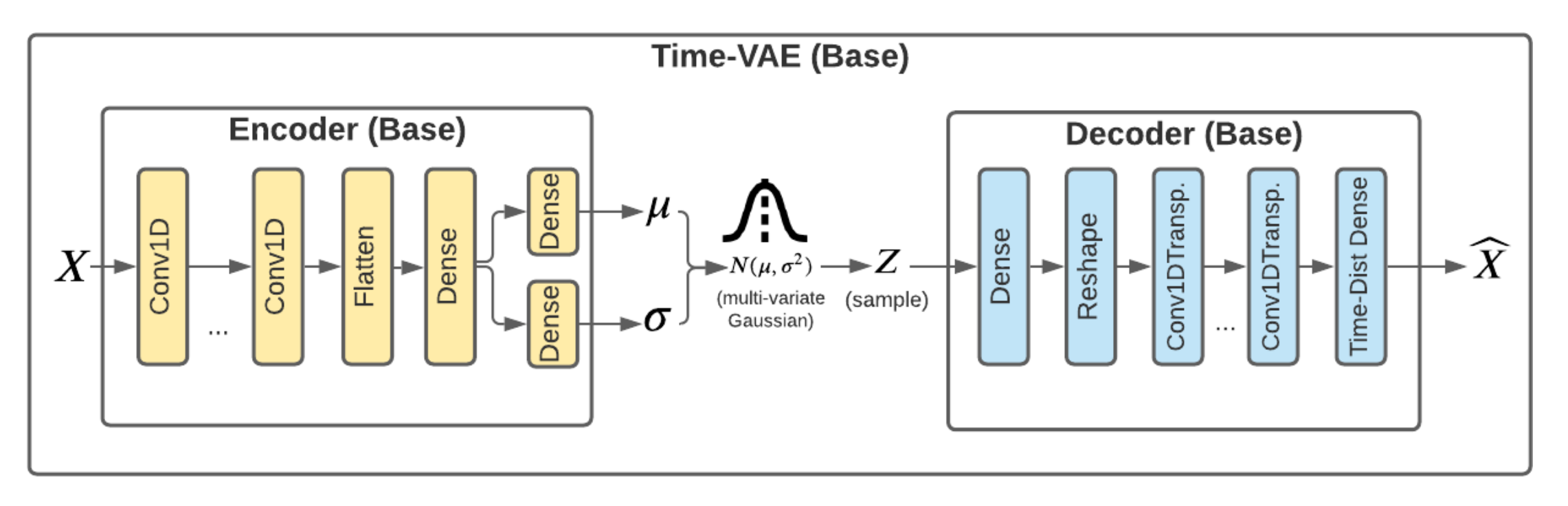
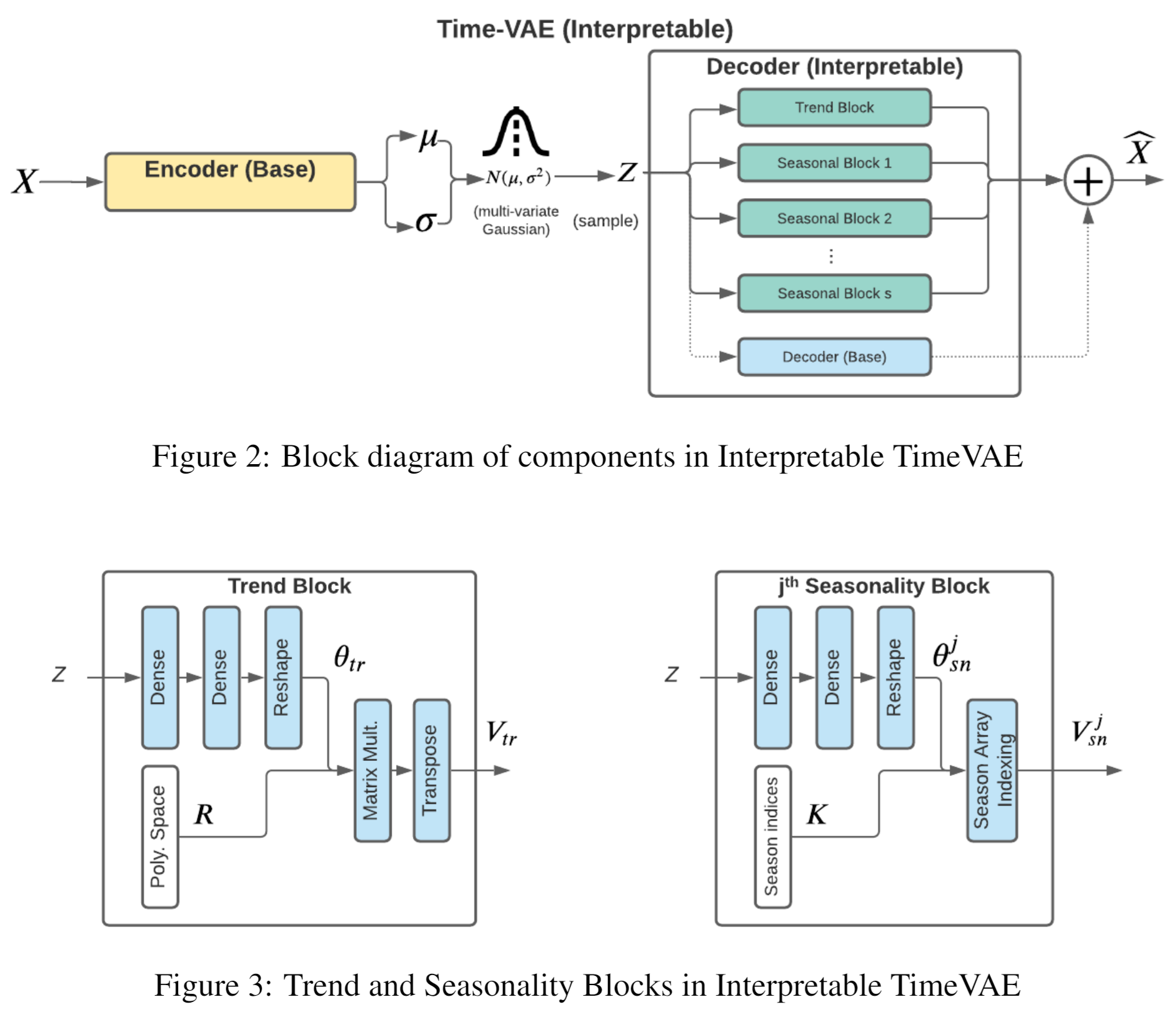
TimeVAE
abudesai/timeVAE: TimeVAE implementation in keras/tensorflow
abudesai/syntheticdatagen: synthetic data generation of time-series data